математика. матем. Применим признак Даламбера и найдем предел Т. к предел меньше единицы, то исследуемый ряд сходится

• Название: Применим признак Даламбера и найдем предел Т. к предел меньше единицы, то исследуемый ряд сходится
• Анкор: математика
• Дата: 02.10.2021
• Размер: 112.8 Kb.
• Имя файла: матем.docx
• Тип: Документы; #240126

1.1. ;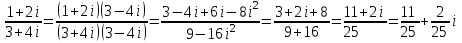

1.2.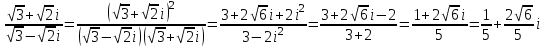

;

2.1. ;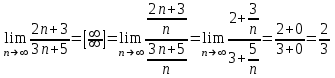

2.2.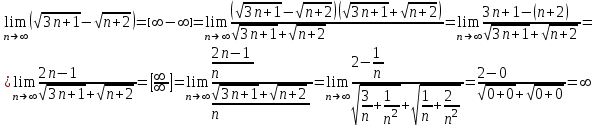



3.1.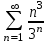

Применим признак Даламбера и найдем предел: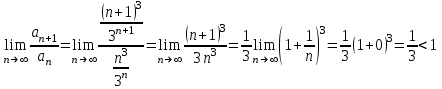



Т.к. предел меньше единицы, то исследуемый ряд сходится.

3.2. .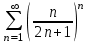

Используем радикальный признак Коши и найдем предел: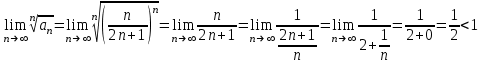



Т.к. предел меньше единицы, то исследуемый ряд сходится.

4.1.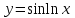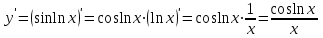

;

4.2.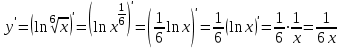

;

5.1.

Применим формулу интегрирования по частям .

Тогда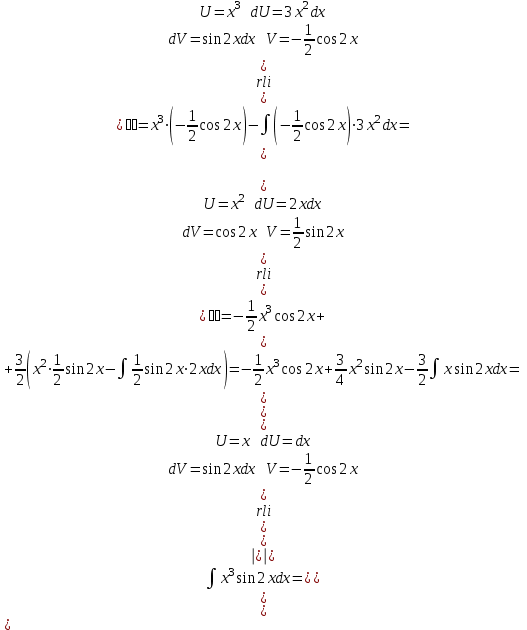



5.2.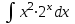

Применим формулу интегрирования по частям .

Тогда



6.1.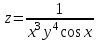

Найдем частные производные первого порядка:





Найдем частные производные второго порядка: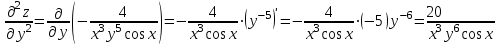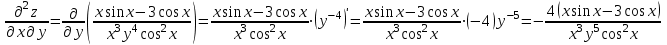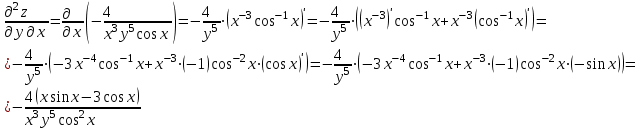









6.2.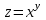

Найдем частные производные первого порядка: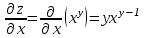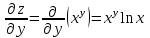





Найдем частные производные второго порядка: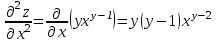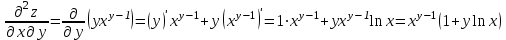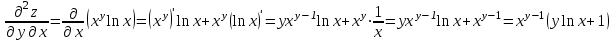









7.1. ,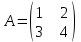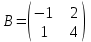



7.2. ,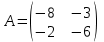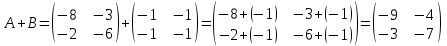



8.1. ,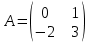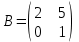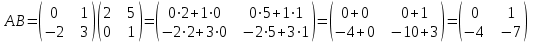



8.2. ,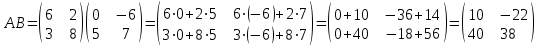



9.1.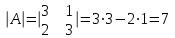



9.2.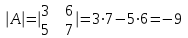



10.1.

Найдем решение системы методом сложения. Проведем почленное сложение уравнений системы:



Отсюда .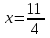

Подставим полученное значение во второе уравнение и найдем :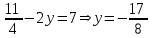



Таким образом, получили решение .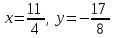

10.2.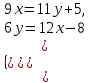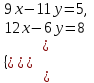



Найдем решение системы методом сложения.

Умножим все члены первого уравнения на 4, умножим все члены второго уравнения на (-3):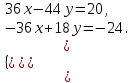



Проведем почленное сложение уравнений полученной системы: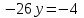



Отсюда .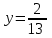

Подставим полученное значение в первое уравнение и найдем :



11.1. , ,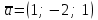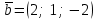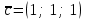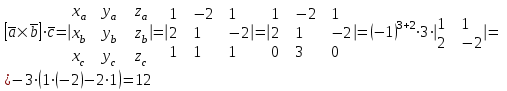



11.2. 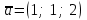, ,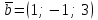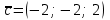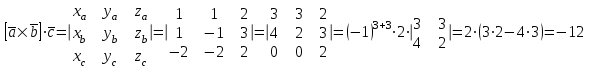