Пример Пусть. Тогда новые функции, будет выглядеть так Определение
 Скачать 58.48 Kb. Скачать 58.48 Kb.
|
|
Сложная функция “Сложный, составной, сложенный или составленный из разных частей…”. Толковый словарь В.И. Даля. Рассмотрим функцию  . Составим новую функцию так, чтобы ее аргументом была другая функция . Составим новую функцию так, чтобы ее аргументом была другая функция 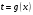 . .Пример: Пусть  . .Тогда новые функции 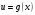 , будет выглядеть так: , будет выглядеть так: Определение. Сложной функцией от х называется функция  , где функция , где функция 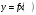 вместо аргумента х используется другая функция вместо аргумента х используется другая функция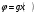 . .Чтобы сложная функция предстала в более наглядном виде, и сделана данная презентация. Сложная функция  определена для тех значений независимой переменной х, для которых значения функции определена для тех значений независимой переменной х, для которых значения функции 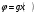 входят в область определения функции входят в область определения функции 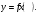 Сложную функцию рассматриваем как композицию двух функций, то есть как последовательное выполнение двух соответствий. Пример:  - сложная функция. Она получена из функции - сложная функция. Она получена из функции 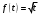 , при замене аргумента на , при замене аргумента на 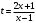 . . , так как область определения функции , так как область определения функции состоит из неотрицательных чисел. Тогда область определения функции состоит из неотрицательных чисел. Тогда область определения функции есть множество  2. Построим график функции  Укажем область определения: D(y) = (-∞; -2] U (2; +∞). Заметим, что это четная функция. Внутренняя функция: g(x) = x2 – 4, построим график в системе координат (х,t). Для простоты изложения мы строим всю параболу, но в дальнейшем рассматриваем только те х, которые входят в множество D(y). Внешняя функция: 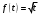 , построим график в системе координат (t,y). , построим график в системе координат (t,y).График исходной сложной функции будем строить в системе координат (х,у). Для наглядности на рисунке отмечено некоторое произвольное значение х0, для него с помощью графика g(x) можно указать t0=g(x0), а для t0 по графику внешней функции находим значение у0=f(t0), таким образом получаем цепочку соответствий: x0 После того, как два вспомогательных графика построены, переходим к главной задаче – построению графика сложной функции. Пусть переменная х изменяется от 2 до бесконечности. По графику g(x) хорошо видно, что при этом переменная t изменяется от 0 до бесконечности. В силу возрастания квадратичной функции на данном участке об этом можно было догадаться и без графика, но график помогает в дальнейших рассуждениях. Итак, переменная t изменяется от 0 до бесконечности. Переходим в систему координат с графиком внешней функции f(t). Значения функции, то есть у, меняются от 0 до бесконечности. Все эти изменения приводятся в таблице на слайде. Значит, для функции  при увеличении аргумента от 2 до бесконечности получаем возрастание функции от 0 до бесконечности. И то, что мы выделили этот участок монотонности, уже очень важно! Можно хотя бы схематично изобразить график при х≥2 при увеличении аргумента от 2 до бесконечности получаем возрастание функции от 0 до бесконечности. И то, что мы выделили этот участок монотонности, уже очень важно! Можно хотя бы схематично изобразить график при х≥2Задание : №1 Составьте сложные функции    , если: , если:   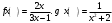 Контрольная работа Из учебника по этой ссылке: https://www.almatykitap.kz/catalog/algebra-dlya-uchaschihsya-10-klassa-obscheobrazovatelnoy-shkoly-16014/ стр.35 №1 и стр:67 №1 а,в |
