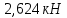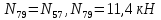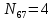Методические рекомендации по выполнению задания 2. Пример выполнения Задания 2 Расчет статически определимой фермы
 Скачать 280.2 Kb. Скачать 280.2 Kb.
|
|
Пример выполнения Задания 2 Расчет статически определимой фермы. Заданная расчетная схема Исходные данные F1 = 3 кН F2 = 5 кН F3 = 4 кН F4 = 5 кН F5 = 3 кН l = 18 м h1 = 3 м h2 = 5 м 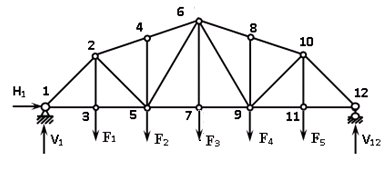 Вычерчиваем ферму в масштабе. Прикладываем заданную внешнюю нагрузку. Проверим геометрическую неизменяемость фермы. а) Проверим выполнение необходимого условия: 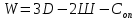 , ,где 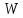 – число степеней свободы, – число степеней свободы,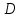 – число стержней, – число стержней, 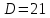 ; ;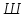 – число одиночных шарниров, соединяющих стержни, – число одиночных шарниров, соединяющих стержни, 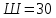 ; ;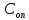 – число опорных стержней (шарнирно-неподвижная опора 1 эквивалентна двум опорным стержням, шарнирно-подвижная опора 12 –одному опорному стержню), – число опорных стержней (шарнирно-неподвижная опора 1 эквивалентна двум опорным стержням, шарнирно-подвижная опора 12 –одному опорному стержню), 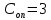 . .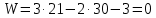 . .Необходимое условие выполнено. Аналитическое условие 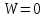 является необходимым условием геометрической неизменяемости и показывает, что система является статически определимой. является необходимым условием геометрической неизменяемости и показывает, что система является статически определимой.б) Проверим выполнение достаточного условия: основу фермы составляют шарнирные треугольники, каждый следующий треугольник образован присоединением двухстержневого звена (одно звено их двух стержней) к предыдущему. Ферма прикреплена к диску «земля» с помощью трех опорных стержней, которые не параллельны друг другу и не пересекаются в одной точке. Таким образом, ферма образована по принципам структурообразования геометрически неизменяемых систем, т.е выполнено достаточное условие геометрической неизменяемости. Вывод: Так как выполнено и необходимое, и достаточное условия геометрической неизменяемости, то заданная система является геометрически неизменяемой системой. Система статически определима. Определим аналитически усилия во всех стержнях фермы. Для начала определяем опорные реакции: 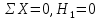 , ,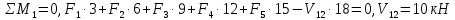 , ,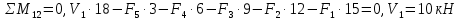 . .Выполним проверку найденных реакций: 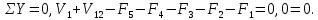 Статическое равновесие сохранено, значит, реакции найдены верно. Определяем внутренние усилия во всех стержнях фермы. Выполним предварительные расчеты: 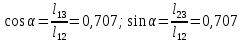 ; ;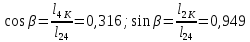 ; ;Вычисляем усилия в стержнях фермы:
Так как ферма симметричная и нагрузка, приложенная к ферме, также симметричная, то усилия в симметрично расположенных стержнях будут равны. Следовательно, рассчитываем только половину фермы, а остальные усилия запишем по аналогии. Результаты аналитического расчета фермы приведены в таблице 1. Таблица 1 – Результаты аналитического расчета
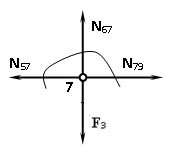
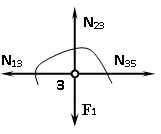
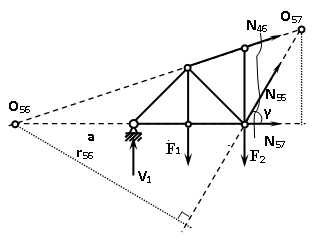
Построение диаграммы Максвелла-Кремоны . Вычерчиваем ферму в масштабе, прикладывая внешние силы, реакции опор. Обозначаем внешние поля цифрами 1,2,3,4,5,6,7 и внутренние поля буквами а,б,в,г,д,е,ж,з,и,к . При этом будем обходить ферму строго по часовой стрелке. Аналитическим способом определяем реакции: V1 = 10(кН), V12 = 10(кН) В принятом масштабе сил (1см =1кН – масштаб можно выбирать любой, но чем крупнее он , тем точнее расчет), обходя ферму по часовой стрелке, строим из заданных (F1 , F2 , F3 , F4 , F5) и реактивных (V1,V12)сил замкнутый силовой многоугольник (силовую линию) 1-2-3-4-5-6-7-1. Из точки 1 откладываем вверх V12, получаем точку 2 (по ходу часовой стрелки за полем 1 идет сила V12). Потом из полученной точки 2 вниз (направление силы) откладываем F5 (по ходу часовой стрелки за полем 2 идет сила F5), получаем точку 3. Далее 3 – F4 (вниз) – 4 – F3 (вниз) – 5 – F2 (вниз) – 6 – F1 (вниз) – 7 – V1 (вверх) – 1. Для нахождения точки а из точки 1 проводим прямую параллельную стержню а1 , а через точку 7 прямую - параллельную стержню а7. Точка пересечения прямых а1 и а7 - точка а. Далее через полученную точку а проводим прямую параллельную стержню аб, а через точку 6 - прямую параллельную стержню б6. На пересечении прямых аб и б6 получим точку б. Далее через полученную точку б проводим прямую параллельную стержню бв, а через точку 1 - прямую параллельную стержню в1. На пересечении прямых бв и в1 получим точку в. Далее через полученную точку в проводим прямую параллельную стержню вг, а через точку 1 - прямую параллельную стержню г1. На пересечении прямых вг и г1 получим точку г (точки в и г совпали). Далее через полученную точку г проводим прямую параллельную стержню гд, а через точку 5 - прямую параллельную стержню д5. На пересечении прямых гд и д5 получим точку д. Далее через полученную точку д проводим прямую параллельную стержню де, а через точку 4 - прямую параллельную стержню е4. На пересечении прямых де и е4 получим точку е. Далее через полученную точку е проводим прямую параллельную стержню еж, а через точку 1 - прямую параллельную стержню ж1. На пересечении прямых еж и ж1 получим точку ж. Далее через полученную точку ж проводим прямую параллельную стержню жз, а через точку 1 - прямую параллельную стержню з1. На пересечении прямых жз и з1 получим точку з ( точки ж и з совпали) . Далее через полученную точку з проводим прямую параллельную стержню зи, а через точку 3 - прямую параллельную стержню и3. На пересечении прямых зи и и3 получим точку и. Далее через полученную точку и проводим прямую параллельную стержню ик, а через точку 1 - прямую параллельную стержню к1. На пересечении прямых ик и к1 получим точку к (прямая параллельная стержню к2 также должна пройти через точку к). Полученная диаграмма приведена на рисунке 1. Измеряем длину отрезка а1 на диаграмме в масштабе сил. Полученная длина будет являться величиной усилия в стержне а1. Длина отрезка а7 – величина усилия в стержне а7, длина отрезка аб – величина усилия в стержне аб и т.д.. На диаграмме точки в и г совпали, значит длина отрезка вг равна 0, а следовательно усилие в стержне вг равно 0 (аналогично усилие в стержне жз равно 0). На схеме фермы обходим по часовой стрелке узел в котором сходятся стержни а1 и а7, устанавливая при этом название каждого из стержней. Получаем 1а (так как по часовой стрелке сначала идет поле 1, а потом поле а). Таким образом, движение на диаграмме должно идти от точки 1 к точке а, мысленно переносим это направление на схему фермы в заданный узел. Получается, что усилие направленно в узел, а следовательно оно сжимающее и имеет знак минус. Для стержня - а7 ( сначала поле а, потом поле 7). Таким образом, движение на диаграмме должно идти от точки а к точке 7, мысленно переносим это направление на схему фермы в заданный узел. Получается, что усилие направленно из узла и следовательно, оно растягивающее и имеет знак плюс. Аналогичным образом определяем знаки всех усилий в стержнях фермы. Таким образом, обходя каждый узел фермы по часовой стрелке, определяем знаки усилий во всех стержнях фермы. Полученные результаты графического расчета также сведем в таблицу 2. Вывод: Сравнивая результаты аналитического расчета и графического расчета, видим, что результаты получились аналогичными с допустимой относительной погрешностью не более 3%. Таблица 2 – Результаты графического расчета
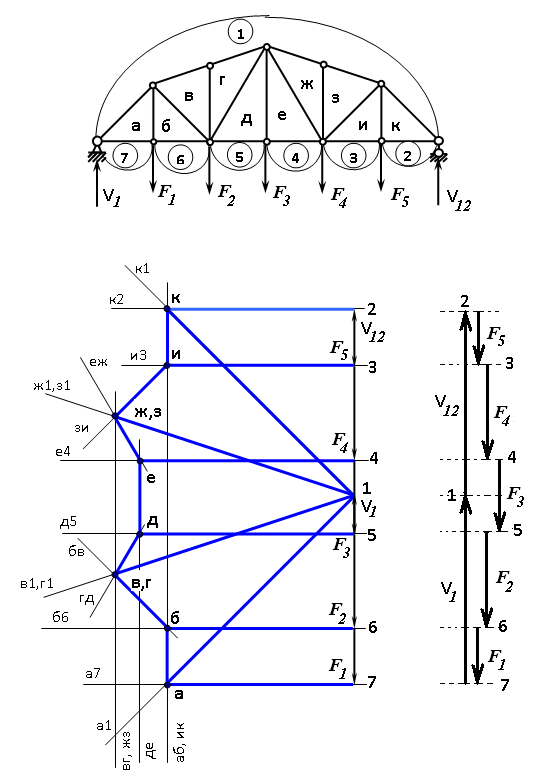 Рисунок 1 – Диаграмма Максвелла – Кремоны Построение линий влияния Линия влияния V1 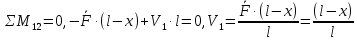 Так как зависимость линейная, то достаточно двух точек для построения линии: х = 0 → V1 = 1, х = l → V1 = 0 Итак под узлом 1, на левой опорной вертикали, откладываем 1 (F находится в узле 1), а под узлом 12, на правой опорной вертикали - нуль ( F находится в узле 12). Полученные точки соединяем прямой линией. Полученное очертание является линией влияния опорной реакции V1 Линия влияния V12 . 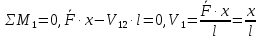 Так как зависимость линейная, то достаточно двух точек: х = 0 → V12 = 0, х = l → V12 = 1 Итак под узлом 1, на левой опорной вертикали, откладываем нуль (F находится в узле 1), а под узлом 12, на правой опорной вертикали - 12 ( F находится в узле 12). Полученные точки соединяем прямой линией. Полученное очертание является линией влияния опорной реакции V12. Линии влияния усилий N68 , N69 , N79 (способ моментной точки) Так как ферма с ездой понизу, следовательно, подвижный единичный груз будем перемещать по нижнему поясу фермы. Выведем функциональные зависимости для заданных усилий, попавших в сечение. а) F находится левее сечения ( F в узлах 1,3,5,7). Рассматриваем равновесие правой отсеченной части фермы. линия влияния N68 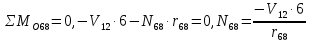 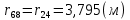 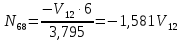 л 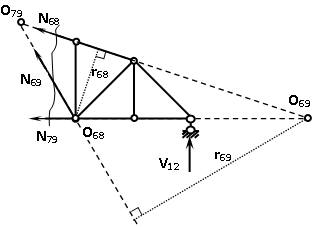 иния влияния N69 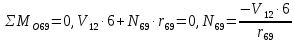 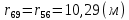 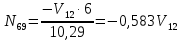 линия влияния N79 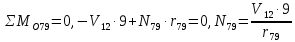 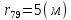 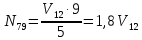 б 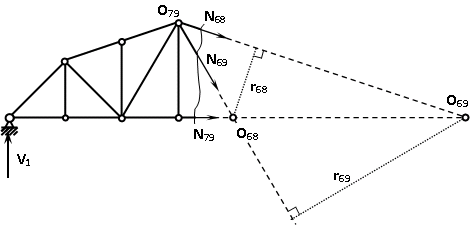 ) F находится правее сечения (F в узлах 9,11,12). Рассматриваем равновесие левой отсеченной части фермы. линия влияния N68 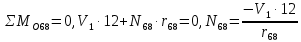 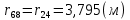 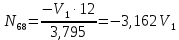 линия влияния N69 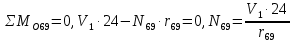 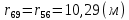 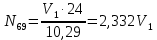 линия влияния N79 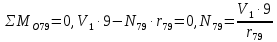 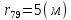 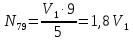 в) Построение линии влияния N68 : 1) строим линию N68 = -3,162 V1 также как линию влияния V1, только все ее значения умножены на коэффициент (–3,162), т.е переворачиваем линию вниз. На эту линию сносим узлы 9,11,12 – получаем 1 правую прямую; 2) строим линию N68 = -1,581 V12 также как линию влияния V12, только все ее значения умножены на коэффициент ( -1,581) (перевернута вниз). На эту линию сносим узлы 1,3,5,7 – получаем 1 левую прямую; 3) полученные вершины первой правой и первой левой прямой соединяем передаточной прямой (вершины под узлами 7 и 9). Полученное очертание и есть линия влияния N68 г) Построение линии влияния N69 : 1) строим линию N69 = 2,332V1 также как линию влияния V1, только все ее значения умножены на коэффициент 2,332 . На эту линию сносим узлы 9,11,12 – получаем 1 правую прямую; 2) строим линию N69 = - 0,583V12 также как линию влияния V12, только все ее значения умножены на коэффициент (- 0,583) (перевернута вниз). На эту линию сносим узлы 1,3,5,7 – получаем 1 левую прямую; 3) полученные вершины первой правой и первой левой прямой соединяем передаточной прямой (вершины под узлами 7 и 9). Полученное очертание и есть линия влияния N69 д) Построение линии влияния N79 : 1) строим линию N79 = 1,8V1 также как линию влияния V1, только все ее значения умножены на коэффициент 1,8 . На эту линию сносим узлы 9,11,12 – получаем 1 правую прямую; 2) строим линию N79 = 1,8V12 также как линию влияния V12, только все ее значения умножены на коэффициент 1,8 . На эту линию сносим узлы 1,3,5,7 – получаем 1 левую прямую; 3) полученные вершины первой правой и первой левой прямой соединяем передаточной прямой (вершины под узлами 7 и 9). Полученное очертание и есть линия влияния N79 Линии влияния опорных реакций и внутренних усилий приведены на рисунке 2. Р 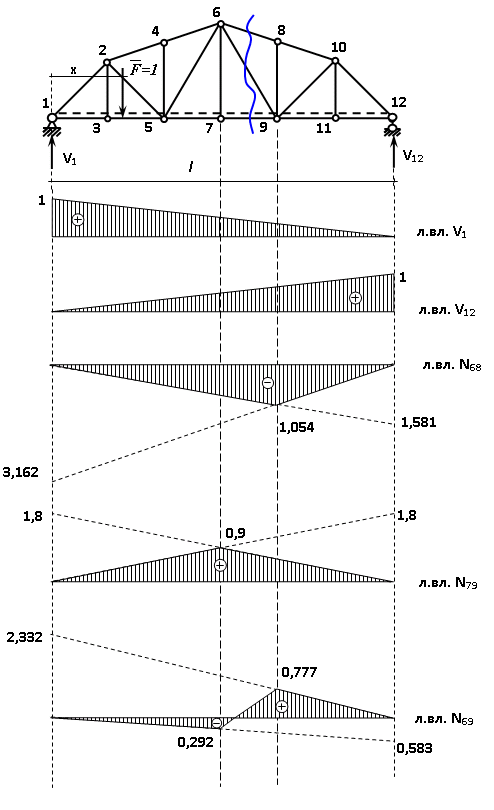 исунок 2 – Линии влияния опорных реакций и внутренних усилий. О 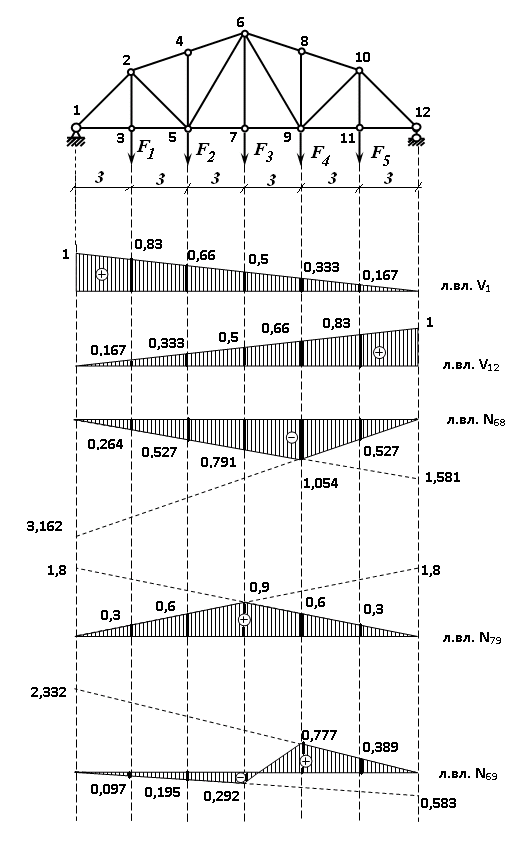 пределение опорных реакций и внутренних усилий по линиям влияния. 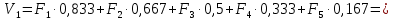 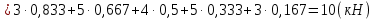 , ,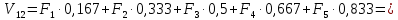 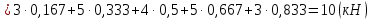 , ,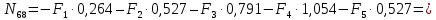 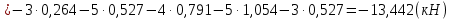 , ,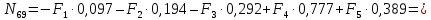 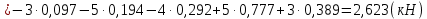 , ,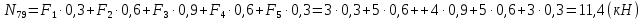 . .Вывод: полученные результаты аналитического расчета , графического расчета и определение усилий по линиям влияния совпадают с точностью допустимой погрешности (не более 3%). |

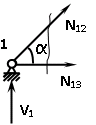
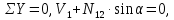
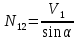 ,
,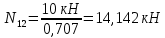
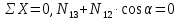 ,
,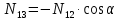 ,
,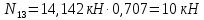
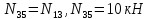
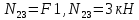
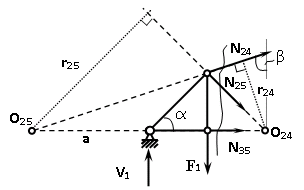
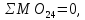
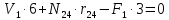
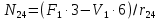
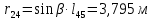
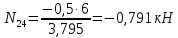
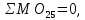
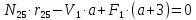
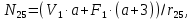
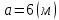
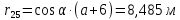
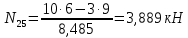
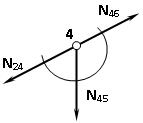
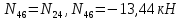
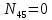
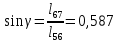
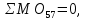
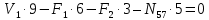
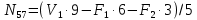
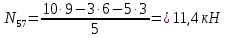
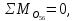
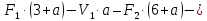
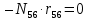
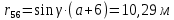
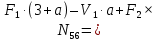
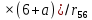
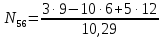 =
=