коллоквиум по теор физике. коллок 1. Примерный перечень вопросов

• Название: Примерный перечень вопросов
• Анкор: коллоквиум по теор физике
• Дата: 07.01.2022
• Размер: 1.84 Mb.
• Имя файла: коллок 1.docx
• Тип: Документы; #325283

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ВОПРОСОВ

1. Твердость. Измерения твердости по Роквеллу, Бринеллю, Кнупу, Виккерсу.

Твердость – мера сопротивления материала локализованной пластической деформации.

Твердость – это сопротивление тела внедрению индентора – другого твердого тела.

Под твёрдостью понимают способность материалов сопротивляться упругой деформации, пластической деформации и (или) разрушению в поверхностном слое.

В технической литературе твердость всегда обозначается буквой Н (от англ. hardness – твердость). Следом за буквой Н всегда пишется одна или две буквы, обозначающие метод испытания твердости, например: НВ – твердость по Бринеллю; HRA, HRB, HRC – твердость по Роквеллу (по шкалам А, В и С); HV – твердость по Виккерсу; HSD – твердость по Шору; HP – твердость по Польди; Нµ – микротвердость и т.д.

Метод измерения по Роквеллу

Измерения твердости по Роквеллу представляют собой наиболее распространенный метод испытаний такого рода, поскольку они просты и не требуют высокой квалификации исполнителя. Используя различные комбинации разных инденторов, можно построить несколько различных шкал твердости, которые позволяют проводить измерения с любыми известными металлическими сплавами (а также с полимерами). Инденторы представляют собой шарики, изготовленные из закаленной стали. Диаметры шариков составляют 1/16, 1/8, 1/4 и 1/2 дюйма (1,588; 3,175; 6,350 и 12,70 мм, соответственно). Инденторы также изготавливают из алмазов в виде конусов (инденторы Брайля), которые применяют при испытании наиболее твердых материалов.

Оценка твердости по методу Роквелла основана на определении разности глубин вдавливания при последовательном приложении сначала небольшой (минимальной) нагрузки и последующей большой (максимальной) нагрузки. Предварительное использование небольшой нагрузки повышает точность измерений. Выбор различных значений минимальной и максимальной нагрузки позволяет производить испытания двух типов: стандартные испытания по Роквеллу и измерения поверхностной твердости по Роквеллу. В обычном методе Роквелла минимальная нагрузка составляет 10 кг, а максимальная нагрузка может быть задана равной 60, 100 и 150 кг. Каждая шкала задается определенной буквой алфавита. Некоторые из них, с указанием соответствующих им инденторов и нагрузок , приведены в таблицах 9.2 и 9.3, а.

При измерениях поверхностной твердости минимальная нагрузка принимается равной 3 кг, а максимальные нагрузки могут составлять 15, 30 или 45 кг. Соответственно, в зависимости от выбора индентора, шкалы при измерении поверхностной твердости обозначаются буквами N, T, W, X и Y. Данные, относящиеся к шкалам, используемым для измерения поверхностной твердости, приведены в таблице 9.3, б.

При указании показателя твердости по Роквеллу и поверхностной твердости необходимо приводить не только значение числа твердости, но и ссылаться на шкалу, к которой это значение относится. Шкала маркируется символом HR с добавлением соответствующего обозначения шкалы. Например, показатель твердости 80HRB обозначает: "Твердость 80 единиц по шкале В", а обозначение 60HR30W расшифровывается так:" Твердость 60 единиц по шкале 30W".

Верхний предел каждой шкалы соответствует 130 единицам. Но если в любой шкале измеряемое значение твердости превышает 100 единиц и оказывается меньше 20 единиц, то оценки становятся недостоверными, а поскольку шкалы перекрываются, то в такой ситуации предпочтительно воспользоваться шкалами, соответствующими более жестким или более мягким материалам.

Неточность измерений может быть также следствием того, что испытуемый образец был чрезвычайно тонким или же измерения проводились слишком близко к его краю, или же два последовательных измерения были сделаны очень близко друг к другу. Толщина образца должна быть, по крайне мере, в 10 раз больше глубины вдавливания индентора, а расстояние между центром индентора и краем образца или между двумя точками, в которых производятся замеры, не должно быть меньше трех диаметров индентора. Не рекомендуется производить измерения твердости на образцах, уложенных друг на друга. Точность измерений также зависит от того насколько гладкой была поверхность, на которой производились измерения.

Современная аппаратура для измерения твердости по Роквеллу автоматизирована, и выполнять измерения очень легко. Показатели твердости непосредственно считываются на дисплее прибора, а сам процесс измерений занимает несколько секунд. Кроме того, в современных приборах существует возможность варьировать длительность приложения нагрузки. Этот фактор также необходимо принимать во внимание при интерпретации экспериментальных данных.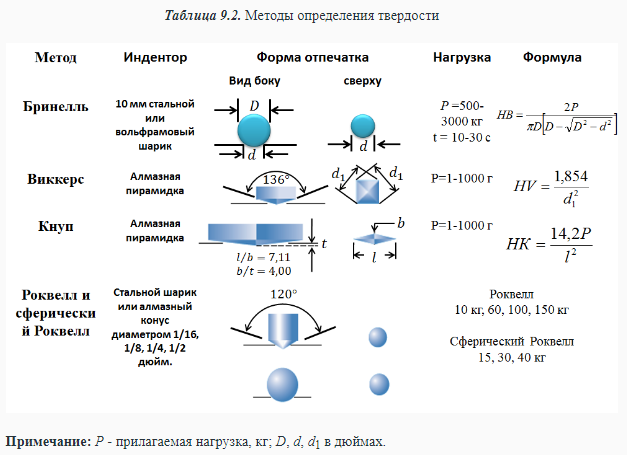 




Метод по Бринеллю

При определении твердости по Бринеллю, так же как и при испытаниях по Роквеллу, сферический индентор вдавливается в поверхность исследуемого металлического образца. Диаметр шарика, изготовленного из закаленной стали или карбида вольфрама составляет 10 мм. Стандартные нагрузки лежат в пределах от 500 до 3000 кг, изменяясь ступенями по 500 кг. В процессе испытаний нагрузка поддерживается постоянной в течение заданного времени (от 10 до 30 с). Чем выше твердость материала, тем больше должна быть нагрузка.

Показатель твердости по Бринеллю HB зависит как от величины приложенной нагрузки, так и от диаметра полученного отпечатка (см. табл. 9.2). Диаметр отпечатка измеряется с помощью специального микроскопа с низким разрешением с использованием шкалы, нанесенной на окуляр.

Величина измеренного диаметра затем, с помощью специальной карты, пересчитывается в соответствующий показатель твердости. В методе Бринелля используется только одна шкала. 

Измерения твердости по Бринеллю осуществляются с помощью полуавтоматической техники. Для этого применяют оптическую сканирующую систему, состоящую из цифровой камеры, которая устанавливается на гибкой опоре. Это позволяет правильно позиционировать камеру над отпечатком. Данные измерений с камеры передаются на компьютер, который анализирует полученные результаты, определяет размеры отпечатка и вычисляет показатель твердости по Бринеллю.

При использовании такой техники требуется более тщательная обработка поверхности, чем при замерах, осуществляемых вручную.

Требования к толщине образца, а также к расстояниям между точкой измерения и краем образца и между точками независимых измерений такое же, как и в методе испытаний по Роквеллу. Необходимо также, чтобы отпечаток был достаточно ясным. Для этого следует проводить измерения на гладкой и ровной поверхности.

Метод Виккерса и Кнупа

Два других используемых метода измерения твердости - это методы Кнупа и Виккерса (или метод алмазной пирамидки). В обоих случаях в качестве индентора используют алмазную пирамидку, которая вдавливается в поверхность исследуемого образца. Прикладываемая нагрузка, которая используется в этих метода, существенно ниже, чем в испытаниях по Роквеллу и Бринеллю. Она лежит в диапазоне от 1 до 1000 г. Создаваемый при этом отпечаток измеряется с помощью микроскопа, и результаты пересчитываются в показатель твердости (табл. 9.2). Для выполнения испытаний необходима тщательная подготовка поверхности - шлифовка и полировка. Показатели твердости по Кнупу и Виккерсу обозначаются символами HK и HV. Шкалы твердости для обоих методов практически совпадают.

Исходя из используемых размеров индентора, оба метода иногда называют измерениями микротвердости. Оба метода пригодны для оценки твердости небольших образцов или малых областей на образце. На рисунке 9.4. показано, что в силу очень малого размера индентора (черные отпечатки ), метод позволяет измерять микротвердость в отдельных зернах Это справедливо также для структурных составляющих сплавов и неметаллических включений. Метод Кнупа используют для измерения твердости таких хрупких образцов как керамики.



Современные приборы для измерения микротвердости представляют собой автоматизированные устройства, в которых индентор соединен с анализатором изображений, передающим сигнал на компьютер, снабженный соответствующим программным обеспечением. При помощи используемой системы измерений контролируются такие важные параметры, как расположение места выполнения измерений, положение индентора, расчет значений показателя твердости и величина твердости в испытаниях на процарапывание.

На практике также часто используют другие методы измерений твердости, но мы не будет здесь рассматривать их подробно. К их числу относятся определение микротвердости ультразвуковым методом, динамический тестер (Scleroscope), дюрометр (для пластмасс и эластомеров) и метод оценки стойкости к процарапыванию. Эти методы подробно описаны в литературе, список которой приведен в конце лекции.
2. Пересчет значений твердости. Корреляция между твердостью и пределом прочности.

Таблицы пересчета значений твердости

Желательно располагать методом пересчета значений твердости из одной шкалы в другую. Однако, так как твердость не является строго определенным параметром материала, а так же по причине несовпадения методик различных измерений, пересчетных формул или достаточно полных схем не существует. Таблица для пересчета значений твердости из одной шкалы в другу основаны на эмпирических оценках. Причем установлено, что соответствие между различными шкалами зависит от типа и характеристик конкретного материала.

Наиболее надежные пересчетные таблицы существуют для сталей. Некоторые используемые для этого номограммы показаны на рисунке 9.5. для шкал Кнупа, Бринелля и Роквелла. Также представлена шкала Мооса. Детальные пересчетные таблицы можно найти в литературе, приведенной в конце лекции. Тем не менее, как было сказано выше, к использованию таких пересчетных таблиц следует подходить с осторожностью.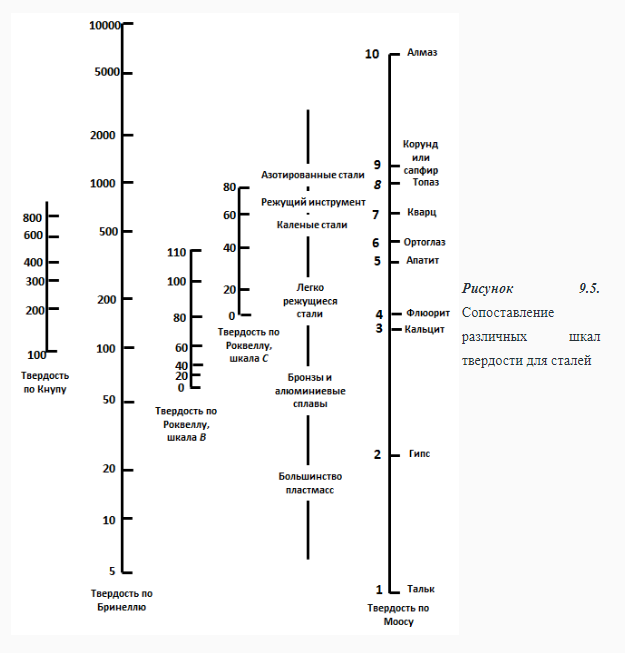



Корреляция между твердостью и пределом прочности

Как предел прочности, так и твердость сталей характеризуют их сопротивление развитию пластических деформаций. Соответственно, ни примерно пропорциональны друг другу, как это показано на рисунке 9.6. Здесь показана зависимость предела прочности от HB для литого чугуна, стали и бронзы. Такая простая пропорциональность, как это показано на рисунке 9.6, выполняется не для всех металлов.



Существует эмпирическое правило, связывающее показатели HB для большинства сталей с пределом прочности (σпп):



3. Вариация свойств материалов. Расчет среднего и стандартного отклонения. Коэффициент безопасности.

Обсудим некоторые вопросы, которые вызывают непонимание студентов, готовящихся стать инженерами. Эти проблемы связаны с тем, что измеряемые свойства материалов не представляют собой точных показателей их свойств. Действительно, даже если мы располагаем наиболее точными из возможных средствами измерений и тщательно контролируем процесс измерений, все равно результаты, получаемые на образцах, приготовленных из одной и той же партии, всегда оказываются неодинаковыми, что свидетельствует об изменении (вариации) свойств материала. Например, допустим, что серия идентичных образцов, изготовленных из одной и той же заготовки, подвергается испытаниям на растяжение на одном и том же приборе. Наблюдения показывают, что, как правило, деформационные кривые в этом случае будут слегка отличаться друг от друга. Отсюда следует, что и основные показатели свойств материала - модуль упругости, предел текучести, предел прочности - оказываются различными.

Неопределенность получаемых результатов определяется рядом факторов. К их числу относятся детали процедуры измерений, колебания режимов приготовления образцов, опыт оператора, калибровка прибора. Кроме того, в одной и той же партии материала могут существовать неоднородности по составу или же иные различия при переходе от одной партии к другой. Конечно, для минимизации возможного разброса результатов измерений принимаются определенные меры с тем, чтобы исключить влияние указанных факторов, которые приводят к разбросу получаемых данных.

Следует также заметить, что разброс результатов измерений существует и в отношении других характеристик материала, таких как плотность, электропроводность, коэффициент термического расширения.

Для инженера, занятого проектирование изделий, важно понять, что этот разброс и вариация показателей свойств материала неизбежны и должны быть приняты как реальность. Из этого следует, что получаемые экспериментальные данные должны быть подвергнуты статистической обработке и вероятностному анализу. Так, вместо того чтобы задавать вопрос: "Какова прочность этого сплава?", инженер должен уметь отвечать на вопрос: "Какова вероятность того, что данный сплав разрушиться при определенных условиях?". 

Обычно желательно оценить типичное значение измеряемого показателя и степень дисперсии (т.е. разброс) данных для данного свойства материала. Для этого следует найти среднее значение показателя и стандартное отклонение.

Среднее значение некоторой величины получается путем деления суммы всех ее измеренных значений на число измерений. В математических терминах средняя величина некоторого параметра x вычисляется как:







Всегда существует некоторая неопределенность в оценке приложенного напряжения в условиях реальной эксплуатации изделия. Обычно расчет напряжения делается с определенной степенью приближения. Далее, как об этом говорилось выше, механические свойства машиностроительных материалов могут варьироваться, так как в них существуют структурные неоднородности, которые были введены в процессе изготовления и, в некоторых случаях, это может создавать угрозу разрушения материала при его эксплуатации. Следовательно, должны быть использованы определенные способы проектирования материалов и изделий из них для защиты от непредвиденных ситуаций. В 20-ом веке было введено понятие коэффициента безопасности или запаса прочности с тем, чтобы уменьшить механическое напряжение в конструкции. Хотя эта  процедура все еще приемлема для некоторых структурных приложений, она не обеспечивает достаточной безопасности для критически важных приложений, таких как конструкции, используемые в самолетах или структурных компонентах мостов. В настоящее время для решения проблемы безопасности функционирования важных структурных приложений принято, во-первых, использовать материалы, которые имеют адекватную прочность и пластичность, во-вторых, предусматривать избыточность структурных конструкций (т. е., наличие дополнительных или дублирующих элементов конструкций), и, наконец, проводить регулярные проверки для определения наличия недостатков и, при необходимости, удалять или ремонтировать компоненты конструкций.

Для снижения риска развития критических ситуаций, позволяющих избежать разрушения материала или конструкции вводится расчетное напряжение σ_d, которое находится умножением максимально возможной приложенной нагрузки σ_С на  фактор дизайна N’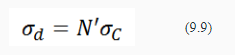



причем N всегда больше единицы.

При выборе материала для конкретного применения величина предела текучести должна быть, по крайне мере, не меньше σ_d. 

В альтернативном варианте расчета определяется безопасное, или рабочее напряжение σ_w, которое используется вместо расчетного напряжения. Определение этого напряжения исходит из величины предела текучести материала, которая делится на коэффициент запаса (или безопасности) N, т.е.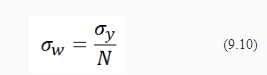



Использование концепции рабочего напряжения (9.9) обычно более предпочтительно, поскольку пр его расчете используется величина реально приложенной нагрузки, а не предел текучести. Обычно неопределенность уровня приложенной нагрузки больше, чем справочного значения предела текучести. Однако в ходе повествования в данной лекции обращалось большое внимание на факторы, влияющие на предел текучести, чем на расчет приложенного напряжения. Поэтому далее будем основываться на использовании понятия безопасного (рабочего) напряжения.

Важную роль играет обоснованный выбор коэффициента безопасности N. Если принять N слишком большим, конструкция получится утяжеленной, т.е. затраты материала будут превышать необходимый уровень. Обычно значения N лежат в пределах между 1,2 и 4,0. Выбор принимаемого при расчете значения N зависит от многих факторов, включая экономические соображения, предшествующий опыт, точность оценки ожидаемых механических нагрузок, а также результатов измерений свойств материала. Самым же главным фактором является важность последствий, к которым приведет разрушение изделия, опасность человеческой жизни и материальные потери.

4. Теоретическая прочность.

в металлических материалах возможны деформации двух типов: упругие и пластические. Пластические деформации сохраняются во времени, а такие характеристики, как прочность и твердость могут служить мерой сопротивления развитию пластических деформаций. На микроскопическом уровне пластические деформации соответствуют суммарному перемещению большого числа атомов в ответ на приложенное напряжение. В ходе такого процесса межатомные связи могут разрушаться, а затем восстанавливаться.

Можно попытаться теоретически рассчитать критическое напряжение, необходимое для сдвига одной части кристалла относительно другой τ_кр. Такой расчёт был впервые выполнен Я.И. Френкелем в 1926 г.

Для простоты рассмотрим простую кубическую решётку с параметром a (рис. 1). Если внешнее напряжение τ приложено так, что появляется возможность сдвинуть одну из атомных плоскостей относительно соседней, то на каждый атом начнёт действовать возвращающая сила химической природы f_хим. Она будет нарастать по модулю по мере удаления атома от равновесного положения x = 0, однако при x = a/2 сила f_хим = 0, поскольку эта точка является положением (неустойчивого) равновесия. Следовательно, на промежутке x = (0 – a/2) график силы должен пройти через минимум. При дальнейшем смещении сила f_хим сменит знак - она будет стремиться переместить атом в следующее положение равновесия x = a. Схематичный график силы показан на рис. 1.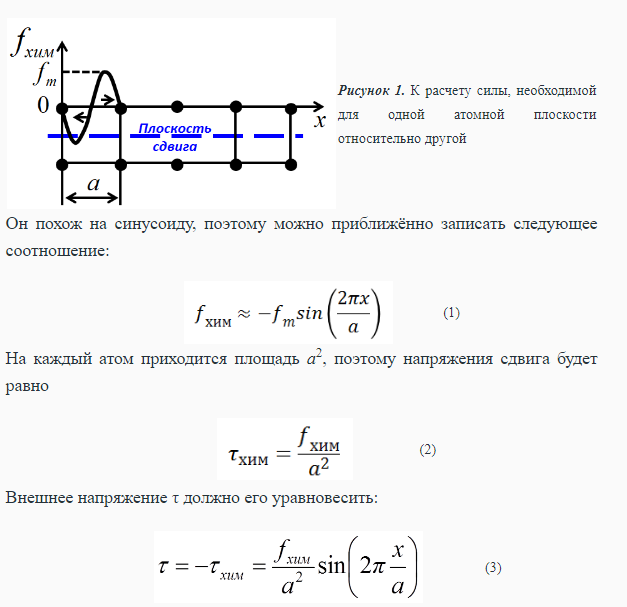 





Из сравнения с законом Гука τ = Gx/a, становится ясно, что теоретическая прочность на сдвиг равна



то есть критическое напряжение сдвига должно составлять примерно) 0,1G. Однако в действительности напряжение сдвига для чистых металлов составляет (10-4 - 10-5) G! То есть теоретическая прочность оказалась на много порядков выше реально наблюдаемых величин. Столь резкое расхождение результатов расчета с опытом заставило Тейлора, Орована и Поляни в 1934 г. предположить, что сдвиг двух атомных плоскостей друг относительно друга и, следовательно, потери механической прочности по сравнению с теоретическим значением, происходит не одновременно, а путём постепенной передачи сдвига от атома к атому. Дефект решётки, осуществляющий такую эстафетную передачу сдвига, был назван дислокацией. Тем не менее, существование таких линейных дефектов было подтверждено прямыми наблюдениями с помощью методов электронной микроскопии только в 50-е годы прошлого столетия. С тех пор была развита теория дислокаций, которая позволила объяснить многие механические и физические особенности поведения металлов, равно как и кристаллических керамик.

5. Дислокации. Плотность дислокаций. Знаки дислокаций.

Линия границы, отделяющей участок сдвига от той части поверхности, на которую сдвиг ещё не распространился, представляет собой искажение кристаллической решётки – дислокацию. Таким образом,  дислокация - это граница незавершенного сдвига.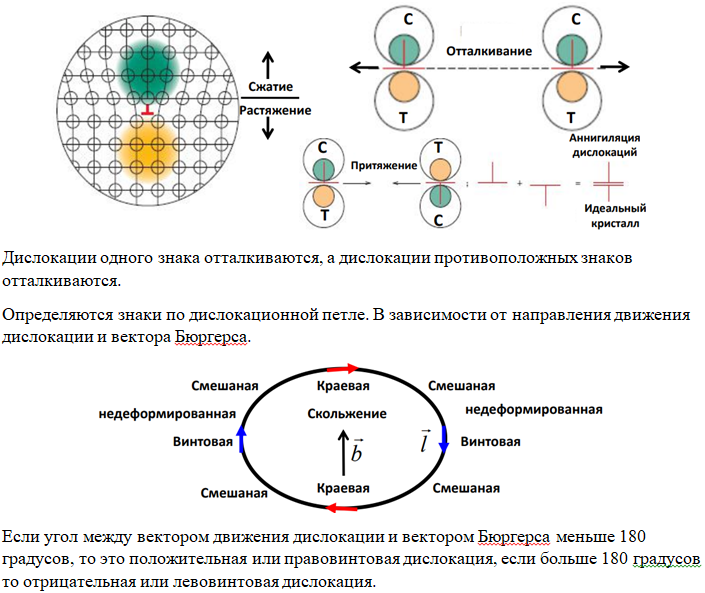





6. Силы, действующие на дислокацию. Энергия дислокации. Сила натяжения дислокационной линии.







7. Механизмы упрочнения металлов. Сила Пайерлса-Набарро.

Важнейшей задачей материаловедов является создание высокопрочных материалов, которые бы, тем не менее, сохраняли определенную пластичность. Обычно пластичность приносится в жертву при создании высокопрочных сплавов. Существуют определенные технологические приемы повышения прочности сплавов. Часто выбор того или иного сплава определяется возможностями достижения требуемого уровня механических характеристик, необходимого для конкретных применений.

Для понимания механизмов упрочнения важно установление соответствия между закономерностями движения дислокаций и механическими свойствами материала. Поскольку наблюдаемые макроскопические пластические деформации определяются движением большого количества дислокаций, то и способность металла к пластическим деформациям зависит от возможности перемещения дислокаций. Твердость и прочность связаны с тем, насколько легко происходят пластические деформации. Поэтому чтобы прочность возрастала необходимо создать препятствия для перемещения дислокаций, поскольку в этом случае для создания пластических деформаций потребуются большие усилия. И напротив, чем более свободно перемещаются дислокации, тем легче металл может деформироваться и тем более мягким и прочным он становится.

Общий принцип упрочнения металла можно сформулировать следующим образом: чем больше ограничений существует для движения дислокаций, тем более твердым и прочным становится материал.



8. Ширина дислокации. Плотноупакованные плоскости. Плотноупакованные направления. Системы скольжения.

Ширина дислокации представляет собой размер зоны в плоскости скольжения, в которой относительное смещение атомов сверху и снизу от плоскости скольжения равно половине максимального смещения.



Для краевой дислокации





9. Дислокации. Напряжения вокруг дислокаций разного вида.



две параллельные краевые дислокации скользят в одной плоскости, Дислокация b1 создаёт в месте нахождения дислокации b2 напряжение, действующее в общей плоскости скольжения дислокаций в направлении их векторов Бюргерса.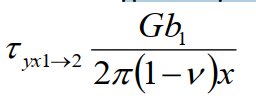



Сложнее взаимодействие краевых дислокаций, скользящих в
параллельных плоскостях. Пусть расстояние между плоскостями скольжения равно h.



10. Возникновение и размножение дислокаций. Источник Франка-Рида.

Дислокации возникают при кристаллизации или охлаждении кристаллов после исчезновения жидкой фазы. Все теории о возникновении дислокаций сводятся к образованию локальных участков концентрации напряжений на границе твердых и жидких фаз. Эта концентрация возникает в результате термических градиентов, изменения состава и структуры кристалла, наличия примесей, вакансий, различных случайностей рода кристаллов, размножения зародившихся на первых этапах кристаллизации дислокаций и др.

Размножение дислокаций. В процессе пластической деформации иод действием внешнего напряжения дислокация движется, увеличивая область кристаллического материала, охваченную пластическим сдвигом. При выходе на поверхность она исчезает, образуя ступеньку, равную вектору Бюргерса.

Источник Франка-Рида

 Дислокация расположена в полости скольжения, совпадающей с плоскостью чертежа. В точках дислокация закреплена. Под действием внешнего напряжения τ она начинает выгибаться и в какой-то момент принимает форму полуокружности, а затем уже и окружности. Под действием напряжения τ внешняя петля расширится соответственно перемещению её отдельных участков, имеющих различную ориентацию, а внутренний отрезок дислокации будет выгибаться вновь и повторит при перемещении цикл.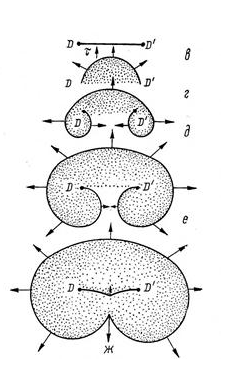



11. Плотность дислокаций. Ядро дислокации.

Плотность дислокаций в кристалле определяется как среднее число линий дислокаций, пересекающих внутри тела площадку площадью 1  , или как суммарная длина линий дислокаций в объеме 1  .



Ядро дислокации – это область вблизи линии дислокации с наибольшими искажениями кристаллической структуры, в которой не «работает» линейная теория упругости. Радиус ядра дислокации составляет несколько значений вектора Бюргерса. (Область наибольших искажений вблизи линии дислокации называется ядром дислокации.)

12. Движение дислокаций. Геометрия скольжения.

Виды движения дислокаций.Скольжение; поперечное скольжение; переползание.

А. Скольжение дислокаций. Консервативная форма движения дислокаций по данной системе скольжения. Система скольжения состоит из комбинации: плоскости скольжения, т. е. воображаемой плоскости в решетке, по которой происходит скольжение (параллельно плоскости решетки с наивысшей плотностью упаковки атомов), и направления скольжения, т. е. наиболее плотноупакованного кристаллографического направления, лежащего в данной плоскости скольжения дислокации.

В результате трансляции атомных слоев по плоскостям скольжения при пластической деформации на поверхности кристалла появляются ступеньки, которые на шлифах видны как линии скольжения или полосы скольжения; обычно при микроскопическом изучении структуры деформированных металлов их называют следами скольжения.

Б. Переползание. Неконсервативное движение дислокаций (рис. 1.23).



Краевая дислокация может покидать свою плоскость, оставляя при этом вакансии (или наращивая к краю экстраплоскости дополнительное число атомов) В первом случае экстраплоскость укорачивается, во втором — удлиняется. Процесс зависит от температуры (является термически активируемым). Переползание, таким образом, связано только с перемещениями вблизи линии краевой дислокации. Могут возникать пороги на дислокации. Такие пороги на линии дислокации образуются также при пересечении дислокаций, движущихся по пересекающимся плоскостям, при этом порог и b не лежат в одной плоскости. Пороги на винтовой дислокации (1) и краевой дислокации (2)—см. рис. 1.24.

В. Поперечное скольжение. Винтовые дислокации в отличие от краевых могут легко менять свою плоскость скольжения на, например, перпендикулярную ей [рис. 1.25, где 1 — первоначальная плоскость; 2 — плоскость поперечного скольжения; 3 (ана­логичная 1)— плоскость скольжения, по которой движение винтовой дислокации будет осуществляться без препятствий]. 


13. Система скольжения. Связь сдвигового и приложенного напряжений.

Система скольжения состоит из комбинации: плоскости скольжения, т. е. воображаемой плоскости в решетке, по которой происходит скольжение (параллельно плоскости решетки с наивысшей плотностью упаковки атомов), и направления скольжения, т. е. наиболее плотноупакованного кристаллографического направления, лежащего в данной плоскости скольжения дислокации.



14. Скольжение в ГЦК, ОЦК, ГПУ кристаллах.

Рассмотрим пример ГЦК структуры. В ней существуют четыре плотноупакованные плоскости типа (111) (рис. 4.15, а). В каждой из них лежит по три направления скольжения. Следовательно, имеется 12 основных систем скольжения.

В кристаллах с ОЦК структурой (рис. 4.15, б) основными плоскостями возможного скольжения являются плоскости типа (110) и имеется два направления скольжения с индексами [111] в этих плоскостях. Нетрудно видеть, что общее число основных систем скольжения, так же как и в случае ГЦК структуры, составляет 12.

В кристаллах, имеющих ГПУ структуру (рис. 4.15, в), плоскостями скольжения являются плоскости базиса (0001), а преимущественными направлениями скольжения − направления  . Таким образом, в ГПУ кристаллах имеет место только одна плоскость и три направления скольжения, что в совокупности образует три основные

системы скольжения.



15. Механизмы упрочнения металлов. Дислокации леса.

Сопротивление деформированнию металлических материалов в кристаллическом состоянии формируется четырьмя принципиально различными механизмами. Это твердорастворное, дислокационное, зернограничное и дисперсионное упрочнение. В современных конструкционных материалах чаще всего используется комбинированное взаимодействие нескольких из этих механизмов, нередко всех четырех. Твердорастворное упрочнение основано на введении в кристаллическую решетку металла атомов замещения или внедрения. При этом кристаллическая решетка основного металла искажается вследствие различного размера атомов, образующих твердый раствор. Особенно большие смещения атомов возникают при образовании твердых растворов внедрения (например, атомы углерода или азота в железных сплавах). Дислокации при своем движении должны преодолевать искажения кристаллической решетки, что затрудняет деформацию.

Дислокационное (субструктурное) упрочнение достигается при формировании или скоплении в кристаллической решетке большого числа дислокаций вплоть до плотностей 1010 – 1011 см-2. Дислокации, скользящие через хаотически расположенные неподвижные дислокации, испытывают со стороны последних сопротивление. Благодаря упругому взаимодействию и междислокационным реакциям, дислокации не сохраняют хаотическе расположение, а создают различные субструктуры.

Зернограничное (поликристаллическое) упрочнение. Большинство используемых материалов – поликристаллы. Наличие границ зерен в поликристалле приводит к его упрочнению. При определенном значении напряжения дислокации не могут перейти через границу в другое зерно и начинают тормозиться. Для преодоления границы им необходимо дополнительное напряжение. Экспериментально установлено, что с уменьшением среднего размера зерна d сопротивление деформированию Δσ возрастает в соответствии с эмпирическим соотношением:

Δσ = k d-1/2, где k – коэффициент, не зависящий от размера зерна.

Дисперсионное упрочнение, или упрочнение дисперсными частицами, заключается в образовании мелких выделений второй фазы в матрице основного металла или сплава. Эти выделения могут иметь ту же самую или иную кристаллическую решетку, создавать поля напряжений, быть перерезаемыми или неперерезаемыми для дислокаций. В любом случае они создают дополнительные препятствия для движения дислокаций и могут значительно повышать прочность материала.

Сопротивление со стороны дислокаций леса 1) Упругое взаимодействие; 2) Пересечение дислокаций с образованием стопоров.

Увеличение плотности дислокаций в результате деформации приводит к затруднению движения дислокаций и повышению напряжения. Явление увеличения напряжения в процессе деформации называется наклёпом

16. Разрушение. Теоретические основы разрушения.

Разрушение — это разделение тела на две или более частей, происходящее при приложении статического (т.е. постоянного или медленно изменяющегося во времени).
17. Хрупкое и вязкое разрушение. Концентраторы напряжений.

Различают разрушение хрупкое и вязкое.



Хрупкое разрушение происходит в три стадии:

1) Зарождение микротрещины на дефектах.

2) Подрастание трещины до критического размера.

3) Распространение трещины через весь образец, т.е. возникновение магистральной трещины.

При хрупком разрушении третья стадия происходит самопроизвольно без дополнительного деформирования образца, то есть без дополнительного подвода энергии извне. Трещина растёт за счёт упругой энергии, накопленной на предыдущей стадии деформирования.

Вязкое разрушение происходит обычно после значительной пластической деформации (десятки процентов). Его главными особенностями являются медленное развитие трещин и высокая энергоемкость, обусловленная необходимостью затраты значительной работы пластической деформации у вершины трещины. 



18. Переход от пластичного к хрупкому разрушению.



19. Усталость. Характеристики усталости. Параметры влияния

Усталостью называется разрушение металлов под действием повторных или знакопеременных нагрузок.

Периодическая нагрузка – переменная нагрузка с установившимся во времени характером изменения, значения которой повторяются через определенный промежуток (период) времени.

Цикл напряжений – совокупность всех значений переменных напряжений за время одного периода изменения нагрузки.

Обычно цикл напряжений характеризуется двумя независимыми из следующих основных характеристик (параметров цикла):

σmax – максимальное напряжение цикла (наибольшее в алгебраическом смысле напряжение цикла);

σmin – минимальное напряжение цикла (наименьшее в алгебраическом смысле напряжение цикла);

σm – среднее напряжение цикла (полусумма наибольшего и наименьшего напряжений цикла)





20. Ползучесть. Характеристики ползучести. Параметры влияния

Ползучестьюназывается процесс нарастания остаточной деформации во времени при постоянных нагрузке или напряжении и температуре.

Предел ползучести характеризует напряжение, под действием которого материал может длительное время работать, не подвергаясь значительной деформации. Однако он ничего не говорит о сопротивлении материала разрушению при длительном воздействии температуры и напряжения. Для оценки такого сопротивления определяют предел длительной прочности – наибольшее напряжение, под действием которого материал при данной температуре разрушается через заданный промежуток времени. Время до разруше-

ния называют долговечностью.

Методика проведения испытаний на длительную прочность близка к методике испытаний на ползучесть. Используется обычно та же схема нагружение – растяжение. Для определения предела длительной прочности необходимо провести испытание, по крайней мере, пяти-шести образцов при разных напряжениях. Основным результатом испытания каждого образца является время до разрушения τр при заданном напряжении σ. Связь между τр и σ хорошо аппроксимируется уравнением:

τр = В σ– m,

(11.99)

где В и m – коэффициенты.
21. Критерий Грифитса. Движущая сила. Энергия разрушения.



где σ_крит – наименьшее напряжение растяжения, необходимое для распространения трещины как хрупкой; Е – модуль Юнга;  – поверхностная энергия стенок трещины, отнесенная к единице ее площади; с – половина длины трещины.

При распространении трещины происходит выделение энергии упругой деформации. Вместе с тем образование новых поверхностей (вследствие роста трещины) требует затраты определенной энергии. Согласно критерию Гриффитса, трещина будет самопроизвольно распространяться, если увеличение , связанное с образованием новых поверхностей трещины, будет меньше энергии деформации, которая выделяется в результате роста трещины.



22. Механизмы деформации. Разрушение керамики. Ползучесть.

23. Механизмы деформации и упрочнения полимеров.

24. Фазовые диаграммы. Предел растворимости. Фаза. Твёрдые растворы.

25. Термодинамический метод. Термодинамические потенциалы. Фазовые равновесия.

26. Построение фазовых диаграмм. Кривые охлаждения.

27. Уравнение Холла-Петча.

28. Тведорастворное упрочнение. Взаимодействие дислокаций с примесями.

29. Атмосферы Коттрелла. Полоса Людерса. Эффект Портвина-ле-Шателье-Брауна.

30. Дисперсионное твердение. Срезание, огибание. Напряжение Орована.

31. Изменение механизмов при старении.

32. Виды деформации альтернативные скольжению. Мартенситные преобразования.

33. Сбросообразование

34. Двойникование.