Содержание
Введение
ГЛАВА 1. Принципы работы стека
ГЛАВА 2. Использование стека для организации работы с множествами
Заключение
Список литературы
Приложение
Введение
Любая компьютерная программа предназначена для обработки данных, от способа организации которых зависят алгоритмы работы, поэтому выбор структур данных должен предшествовать созданию алгоритмов. Любой язык программирования содержит стандартные способы организации данных - основные и составные типы. Наиболее часто в программах используются массивы, структуры и их сочетания, например, массивы структур, полями которых являются массивы и структуры.
Цель описания типов данных, состоит в том, чтобы зафиксировать на время выполнения программы размер значений, которые присваиваются этим переменным и, соответственно, фиксировать размер выделяемой области памяти для них. Такие переменные называются статическими.
Память под данные выделяется либо на этапе компиляции , либо во время выполнения программы с помощью операций выделения и очистки памяти .В обоих случаях выделяется непрерывный участок памяти.
Если до начала работы с данными невозможно определить, сколько памяти потребуется для их хранения, память выделяется по мере необходимости отдельными блоками, связанными друг с другом с помощью указателей. Созданные и не описанные заранее, переменные размещаются на свободные участки в динамической области оперативной памяти. Такой способ распределения памяти называется динамическим, а соответствующий способ организации данных называется динамическими структурами данных, поскольку их размер изменяется во время выполнения программы. Из динамических структур в программах чаще всего используются линейные списки, стеки, деки, очереди и бинарные деревья. Они различаются способами связи отдельных элементов и допустимыми операциями. Динамическая структура может занимать несмежные участки оперативной памяти. Динамические структуры широко применяют и для более эффективной работы с данными, размер которых известен, особенно для решения задач сортировки, поскольку упорядочивание динамических структур не требует перестановки элементов, а сводится к изменению указателей на эти элементы. Например, если в процессе выполнения программы требуется многократно упорядочивать большой массив данных, имеет смысл организовать его в виде линейного списка. При решении задач поиска элемента в тех случаях, когда важна скорость, данные лучше всего представить в виде бинарного дерева.
Элемент любой динамической структуры данных представляет собой структуру, содержащую по крайней мере два поля: для хранения данных и для указателя. Полей данных и указателей может быть несколько. Поля данных могут быть любого типа: основного, составного или типа указатель.
В практических программах часто используется реализация динамических структур с помощью массивов. Операции выделения и освобождения памяти - дорогая процедура, поэтому, если максимальный размер данных можно определить до начала использования и в процессе работы он не изменяется (например, при сортировке содержимого файла), более эффективным может оказаться однократное выделение непрерывной области памяти. Связи элементов при этом реализуются не через указатели, а через вспомогательные переменные или массивы, в которых хранятся номера элементов.
Типичной является ситуация, когда одна проблема требует решения другой, которая неразрешима без решения третьей и так далее. В этом ряду проблема, не вызвавшая новых проблем, решается первой, хотя оформилась последней, а исходная проблема решается в последнюю очередь. Такая дисциплина обслуживания часто используется в системном программном обеспечении, компиляторах, в различных рекурсивных алгоритмах. Ей соответствует абстрактная динамическая линейная структура, называемая стек.
Стек - это частный случай однонаправленного списка, добавление элементов в который и выборка из которого выполняются с одного конца, называемого вершиной стека. Другие операции со стеком не определены. При выборке элемент исключается их стека. Говорят, что стек реализует принцип обслуживания LIFO (last in - first out, последним пришел - первым ушел). Стек проще всего представить себе как стопку книг на столе, где добавление или взятие новой книги возможно только сверху. Кстати, сегмент стека назван так именно потому, что память под локальные переменные выделяется по принципу LIFO. Стек проще всего реализовать с помощью массива. Кроме массива элементов, соответствующих типу данных стека, достаточно иметь одну переменную целого типа для хранения индекса элемента массива, являющегося вершиной стека. При помещении в стек индекс увеличивается на единицу, а при выборке - уменьшается. Стеки и принцип LIFO находят очень широкое применение в информатике.
В данной работе рассматривается организация вычислений с использованием стека на примере теоретико-множественных операций над множествами.
Сформулируем цели и задачи курсовой работы.
Цель: Изучение принципов работы стека для организации вычислений на примере теоретико-множественных операций над множествами
Задачи:
Изучить и проанализировать научно-методическую литературу по теме «Организация вычислений с использованием стека».
Написать программу, демонстрирующую работу стека на примере теоретико-множественных операций над множествами.
В вычислительной технике стек получил широчайшее распространение, причем как для организации хранения данных, так и для реализации алгоритмических структур.
ГЛАВА 1. ПРИНЦИПЫ РАБОТЫ СТЕКА
Стек - частный случай линейного односвязного списка, для которого разрешено добавлять или удалять элементы только с одного конца списка, который называется вершиной стека. Если мы удалим элемент, в вершине оказывается следующий. Включение нового элемента как бы проталкивает имеющиеся элементы в сторону дна. Порядок их следования при хранении не нарушается, как и в очередях, массивах и других структурах. Поскольку в каждый момент нужен доступ к одному, верхнему, элементу стека, индексы элементов не нужны.
Наиболее простой из них является стек, представляющий собой последовательность объектов данных, связанных между собой с помощью указателей. Особенность организации структуры стека показана на рис. 1.1.
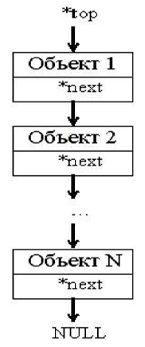
Рис. 1.1: Организация структуры стека
Из рис.1.1. видно, что каждый объект стека связан с последующим с помощью указателя next. Если указатель next равен NULL, то достигнут конец стека. Особенность работы со стеком заключается в том, что новый объект всегда добавляется в начало списка. Удаление также возможно только для первого элемента. Таким образом, данная структура реализует очередь по принципу <первым вошел, последним вышел>. Такой принцип характерен при вызове функций в рекурсии, когда адрес каждой последующей функции записывается в стеке для корректной передачи управления при ее завершении.
Основные операции, которые используются при применении стека:
Сделать пустым.
Добавить элемент. Запись возможна только в верхнюю ячейку стека, при этом вся хранящаяся в стеке информация предварительно проталкивается на одну позицию вниз.
Взять элемент. Чтение допустимо также только из вершины стека. Извлеченная информация удаляется из стека, а оставшееся его содержимое продвигается вверх.
Стек пуст.
Вершина стека: Т.
Процедура <сделать пустым> делает стек пустым, то есть <на дне стека ничего нет>.
Процедура <добавить элемент> добавляет элемент X, типа T, в начало последовательности.
Процедура <взять элемент> применима, если последовательность S
не пустая, она забирает из нее последний элемент, который становится значением переменной X).
Выражение <стек пуст> истинно, если последовательность S пуста.
Выражение <вершина стека> определенно, если последовательность S не пустая, и равно последнему элементу последовательности S.
Особенно явно преимущества стековой организации проявляются при работе в сложных ситуациях, возникающих в программных системах, где на ограниченные ресурсы претендуют несколько конкурирующих задач. Такие ситуации могут встречаться в различных ЭВМ, начиная от небольших однопользовательских систем (при необходимости совместить выполнение фоновой задачи с вводом-выводом) до сложных мультипрограммных систем, управляющих комплексом пользовательских и системных программ. В любом случае от программного обеспечения требуется гибкость, экономия времени выполнения и используемой памяти.
В большинстве процессоров стек (т.е. память со стековым доступом) организован в участке обычной памяти с адресной организацией. Для этого в процессоре имеется специальный регистр - указатель стека Stack Pointer SP. Этот регистр содержит адрес памяти того участка, в который будет осуществляться стековый доступ, а, говоря более точно, адрес "верхушки стека". Указатель стека обычно программно доступен, то есть к нему можно производить обращение как к любому другому регистру.
Рассмотрим области использования стека.
Очень часто некоторые промежуточные результаты работы программы необходимо где-то временно сохранить, прежде чем они будут использованы в дальнейшей обработке. Стек позволяет нам это сделать .Типичная, хотя и не единственная, ситуация заключается в следующем. Пусть некоторому фрагменту программы в машинных командах требуется использовать несколько регистров процессора для хранения промежуточных результатов, которые по окончании его работы уже не будут представлять интереса. Поскольку регистров у процессора не так много, программисты часто стараются не портить их значения без крайней необходимости. Таким образом, с одной стороны, регистры нам действительно нужны, а с другой - не хочется менять их значений..
Рассмотрим простой пример для процессоров с системой команд, принятой в IBM-совместимых компьютерах. Пусть некоторый фрагмент программы должен использовать для промежуточных данных регистры BX и CX. Надежное решение проблемы такое:
SH BX
PUSH CX
<здесь любые манипуляции с BX и CX>
POP CX
POP BX
После завершения работы указанного фрагмента постоянство значений сохраняемых регистров гарантируется независимо от длины и сложности фрагмента [8].
Подобные фрагменты программисты используют настолько часто, что, начиная с процессора Intel 80286, к системе команд записи в стек была добавлена инструкция PUSHA (от push all), сохраняющая в стеке сразу все регистры процессора.
Одним из важнейших предназначений стека является создание возможностей для вызова подпрограмм. Подпрограммой называют некоторый функционально законченный (в котором решается какая-то частная задача) фрагмент программы, оформленный так, чтобы им можно было пользоваться из различных точек основной программы.
Главной проблемой организации подпрограммы является не столько возможность перехода к ней, сколько создание механизма возврата в ту точку, откуда подпрограмма была вызвана, после окончания ее работы. Именно здесь стек и оказывается необычайно полезен. Логика работы подпрограмм является стандартной и строится следующим образом. В конце выделенного фрагмента, оформляемого в виде подпрограммы, ставится специальная инструкция возврата RET (сокращение происходит от return - вернуться). А в любом месте программы, где потребуется выполнить подпрограмму, помещается ее вызов CALL A, где A - адрес начала подпрограммы [10].
Рассмотрим, как происходит процесс вызова подпрограммы, подробнее. Пусть подпрограмма расположена начиная с адреса A, ее вызов - в адресе C, а следующая за вызовом инструкция (точка возврата) - в адресе N (см. рис. 1.2).
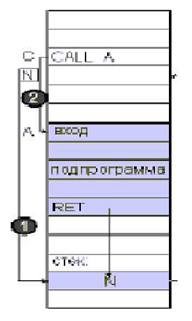
Рис. 1.2: Процесс вызова программы
В принятых обозначениях для перехода к подпрограмме необходимо выполнить два действия:
1) сохранить (в стеке) значение N для последующего возврата;
2) перейти к подпрограмме по адресу A.
Смысл производимых действий становится гораздо более понятным, если учесть, что для хранения адреса очередной команды программы процессор использует специальный регистр - счетчик команд. В процессорах Intel этот регистр обозначается IP (Instruction Pointer) [7]. В новой терминологии смысл перехода к подпрограмме можно сформулировать короче:
1) сохранить в стеке значение PUSH IP;
2) занести A в регистр IP (JMP A).
При возврате из подпрограммы осуществляется обратное действие: из стека извлекается адрес возврата и заносится в IP (POP IP), что обеспечивает переход к этому адресу.
На практике необычайно широко используются вложенные подпрограммы, т.е. одна подпрограмма часто вызывает другую. Очевидно, что здесь способность стека хранить произвольное количество значений и возвращать их по принципу LIFO приходится как нельзя кстати.
Таким образом, мы видим, что благодаря использованию стековой организации памяти процессор получает великолепный механизм организации системы подпрограмм любой степени вложенности[11].
Подчеркнем, что с точки зрения описанного механизма вызова вложенных подпрограмм ситуация, когда подпрограмма вызывает сама себя (на этом базируется так называемая "рекурсия"), ничем не нарушает алгоритма работы (более того, процессору необычайно трудно проверить, вызывает ли подпрограмма другую или саму себя!). Как было указано выше, проблемы здесь заключаются в передаче параметров и создании локальных переменных так, чтобы они "не портили друг друга" при рекурсивных вызовах. Рассмотрим данную проблему подробнее.
Основываясь на уже имеющихся у нас знаниях о стеке, мы можем предположить, что этот вид памяти поможет нам и здесь. Наличие возможности последовательного сохранения вложенных данных, о которой мы уже неоднократно говорили, дает нам ключ и к решению проблемы переменных в процедурах. В наиболее общих чертах это делается следующим образом. При входе в процедуру в стеке выделяется место под локальные переменные подпрограммы, а по завершении работы это место освобождается. Очевидно, что предлагаемый алгоритм прекрасно сочетается с требованиями рекурсии: при каждом вызове в стеке создаются свои собственные копии переменных, которые никак не мешают друг другу.
На практике процесс создания в стеке структур переменных выглядит несколько сложнее, поскольку согласно принципам программирования вложенным процедурам не запрещается пользоваться переменными процедур вышележащих уровней вложенности. Поэтому трансляторы организуют фреймы локальных переменных так, чтобы обеспечивать возможность доступа от фреймов одного уровня к другому [9].
Отметим, что параметры подпрограмм (точнее говоря, их значения или адреса; в первом случае говорят о передаче параметра по значению, а во втором - по ссылке) также передаются при обращении к подпрограмме через стек.
В программировании часто встречаются ситуации, когда одинаковые действия необходимо выполнять многократно в разных частях программы (например, вычисление функции sin x). При этом с целью экономии памяти не следует многократно повторять одну и ту же последовательность команд - достаточно один раз написать так называемую подпрограмму (в терминах языков высокого уровня -процедуру) и обеспечить правильный вызов этой подпрограммы и возврат в точку вызова по завершению подпрограммы. Для вызова подпрограммы необходимо указать ее начальный адрес в памяти и передать (если необходимо) параметры – те исходные данные, с которыми будут выполняться предусмотренные в подпрограмме действия. Адрес подпрограммы указывается в команде вызова CALL, а параметры могут передаваться через определенные ячейки памяти, регистры или стек [6].
Стек используется практически во всех программах, хотя начинающий программист может и не подозревать, что программа работает со стеком. Связано это с тем, что ряд команд работает со стеком неявным образом:
- call - вызов подпрограммы (запоминает в стеке адрес возврата);
- ret - возврат из подпрограммы (берет из стека адрес возврата);
- int n - программное прерывание (запоминает в стеке адрес возврата и регистр флагов);
- iret - возврат из прерывания (выталкивает из стека адрес возврата и восстанавливает флаги) [4].
ГЛАВА 2. ПРОГРАММА РЕАЛИЗУЮЩАЯ РАБОТУ СТЕКА НА ПРИМЕРЕ ТЕОРЕТИКО-МНОЖЕСТВЕННЫХ ОПЕРАЦИЙ НАД МНОЖЕСТВАМИ
Алгоритм вычисления для стековой машины :
Обработка входного символа.
Если на вход подан операнд, он помещается на вершину стека.
Если на вход подан знак операции, то соответствующая операция выполняется над требуемым количеством значений, извлечённых из стека, взятых в порядке добавления. Результат выполненной операции кладется на вершину стека.
2. Если входной набор символов обработан не полностью, перейти к
шагу 1.
3. После полной обработки входного набора символов результат вычисления выражения лежит на вершине стека.
Реализация стековой машины, как программная, так и аппаратная, чрезвычайно проста и может быть очень эффективной. Обратная польская запись совершенно унифицирована - она принципиально одинаково записывает унарные, бинарные, тернарные и любые другие операции, а также обращения к функциям, что позволяет не усложнять конструкцию вычислительных устройств при расширении набора поддерживаемых операций. Это и послужило причиной использования обратной польской записи в некоторых научных и программируемых микрокалькуляторах.
Стек является идеальным средством для вычисления произвольных арифметических и логических выражений. Если предположить, что польская запись поступает в стек поэлементно и каждое поступившее число просто заталкивается в стек, а каждая операция снимает со стека два числа, выполняет с ними свое действие и кладет в стек результат, то в конце стек будет содержать только искомый результат.
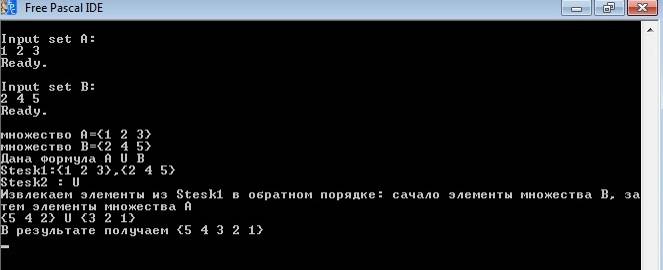
Рис. 2.1: Процесс работы программы
Работа стека продемонстрирована на примере операции объединения двух множеств выполненного в Free Pascal IDE (Рис. 2.1).
Задача заключается в следующем: Дано два множества. Поместить в Stesk1 элементы множеств. А в Stesk2 операцию U (объединения). Затем в результате на выходе программы получаем новое множество состоящее из элементов объединения двух данных множеств, но записанных в обратном порядке. Как и должно быть при извлечении элементов и стека.
Процедуры и функций используемые в программе
Процедура сортировки выбором по не убыванию.
//procedure Sort(var A: TSet; const N: Integer);
var i, j, k: Integer; tmp: T;
begin
for i := 1 to N - 1 do begin
k := i;
for j := i + 1 to N do
if A[j] < A[k] then k := j;
tmp := A[i];
A[i] := A[k];
A[k] := tmp;
end;
end;//
Процедура печати множеств А и В.
//procedure Set_Input(var A: TSet; var N:Integer);
var i, j: Integer; tmp: T; F: Boolean;
begin
Reset(Input);
N := 0;
while not SeekEoLn do begin
Inc(N);
Read(A[N]);
end;
Sort(A, N);
F := False;
i := 1;
while i < N do begin
if A[i] = A[i + 1] then begin
F := True;
Dec(N);
for j := i + 1 to N do
A[j] := A[j + 1];
end
else
Inc(i);
end;
if F then
WriteLn('Repeating elements deleted.');
end;//
Процедура объединения множеств методом слияния.
//procedure Union(var U: TSet; var k: Integer;
const A, B: TSet; const N, M: Integer);
var i, j: Integer;
begin
i := 1;
j := 1;
k := 0;
while (i <= N) or (j <= M) do
if (j <= M) and (i <= N) and (A[i] = B[j])
then begin
Inc(k);
U[k] := A[i];
Inc(i);
Inc(j);
end
else if (j > M) or (i <= N) and (A[i] < B[j])
then begin
Inc(k);
U[k] := A[i];
Inc(i);
end
else begin
Inc(k);
U[k] := B[j];
Inc(j);
end;
end;//
ЗАКЛЮЧЕНИЕ
Развитие вычислительной техники и программирования сопровождалось эволюцией представлений о роли данных, взглядов на их организацию. В большинстве случаев одним из доминирующих свойств компьютеров является способность хранить огромные объемы информации, к которым можно просто обратиться. Информация, подлежащая обработке, в некотором смысле представляет абстракцию некоторого фрагмента реального мира. Мы говорим о данных как об абстрактном представлении реальности, поскольку некоторые свойства и характеристики реальных объектов при этом игнорируются (как несущественные для данной задачи).
Суть всех алгоритмов (и компьютерных программ) состоит в том, что они описывают обработку данных, преобразование некоторых начальных данных в конечные. Какие-то данные алгоритм (программа) может использовать как промежуточные. Естественно, что представление и организация данных имеет при разработке алгоритма первостепенное значение. Вопрос о том, как должны быть организованы данные, необходимо решать до того, как начинается разработка алгоритма (программы)! Ведь прежде, чем выполнить какие-либо операции, нужно иметь объекты, к которым они применяются, и четко представлять себе структуру объектов, которые будут получены.
Представление данных определяется исходя из средств и возможностей, допускаемых компьютером и его программным обеспечением. Однако очень важную роль играют и свойства самих данных, операции, которые должны выполняться над ними. С развитием вычислительной техники и программирования средства и возможности представления данных получили большое развитие и теперь позволяют использовать как простейшие неструктурированные данные, так и данные более сложных типов, которые обладают некоторой организацией.
Рассмотренная в данной работе стековая организация используется для различных целей:
хранения промежуточных результатов и значений параметров;
при обращении к процедуре и организации ее работы;
при получении результатов и выходе из процедуры, для запоминания (упрятывания) и восстановления состояния машины;
при прерывании программы и выходе из прерывания.
Машины со стековой организацией имеют большие преимущества при вычислении сложных выражений. Это можно показать на примере вычисления выражений, в которых используются умножение и деление. При стековой организации памяти могут использоваться команды меньшей длины по сравнению с машинами с регистрами общего назначения, так как не требуют каких-либо разрядов для задания номеров регистров.
Стековые структуры в вычислительных системах относятся к числу фундаментальных и потому чрезвычайно важных. Без способности к перестраиваемой организации данных, в том числе со ссылкой на исполняемый код, компьютеры не были бы таким гибким инструментом, каким они являются сегодня, а были бы просто дорогим калькулятором для специальных целей, имеющим ограниченные возможности и неширокую сферу применения.
В упорядоченных структурах данных стек используется в качестве динамического элемента памяти, в котором абстрактное понятие - аппаратно зависимый стек вызовов - используется для хранения копии данных или их части, будь то адреса памяти элементов данных (передача параметра по ссылке) или копии данных (передача параметра по значению). Самой распространенной задачей обработки списков является сортировка (в лексикографическом порядке, по возрастанию значения, и т. д.), в которой действия машины ограничиваются сравнением всего двух элементов, тогда как список чаще всего содержит миллионы членов.
Существуют различные стратегии (компьютерные алгоритмы), оптимальные для разных типов сортируемых данных, но при реализации все они прибегают к применению программ или подпрограмм, которые обычно вызывают сами себя или часть своего кода рекурсивно, и при каждом вызове добавляют в стек вызовов частично упорядоченный список элементов. Именно по этой причине в курсах структур данных стеки и рекурсии обычно вводятся параллельно, потому что они тесно взаимосвязаны.
Именно благодаря гибкости доступа к стеку вызовов с возможностью перегруппировки данных (организованный по абстрактному методу LIFO блок данных как будто специально придуман только для того, чтобы данные можно было легко переупорядочить) подпрограммы и стандартные функции получают требуемые данные, выполняют те свои задачи, для решения которых они оптимизированы, и передают информацию обратно в вызывающий сегмент программы. Стек вызовов в конкретных случаях включает в себя адрес следующей инструкции вызывающей программы, которая обычно выполняет какие-то действия с откликами, полученными от подпрограмм и стандартных функций. В рекурсивных вызовах эти действия обычно включают сравнение следующего элемента списка с возвратившимся «откликом» (например, выбор из двух значений наибольшей величины), пока список не будет исчерпан. Следовательно, в реальном мире реализаций абстрактного принципа LIFO количество стеков вызовов меняется чрезвычайно часто, размер каждого зависит от числа требуемых элементов данных, которыми необходимо манипулировать.
стек вычисление алгоритм множество
ЛИТЕРАТУРА
Могилев А. В., Пак Н. И., Хеннер Е. К., Информатика, М., «Академия», 2004.
Симонович С.В., Информатика: Базовый курс, СПб: Питер, 2007.
Информатика: Учебник / Под общ. ред. А.Н. Данчула. - М.: И 74 Изд-во РАГС, 2004. - 528 с.
Т. Пратт, М. Зелковиц. Языки программирования: разработка и реализация = Terrence W. Pratt, Marvin V. Zelkowitz. Programming Languages: Design and Implementation. - 4-е издание. - Питер, 2002. - 688 с. - (Классика Computer Science). - 4000 экз. - ISBN 5-318-00189-0.
Каймин В.А. Информатика: Учебник. - М.: ИНФРА-М,2000. - 232 с. - (Серия «Высшее образование»).
Т.А. Павловская С/С++. Программирование на языке высокого уровня. Спб. Питер – 2005.
Гук М.Ю. Процессоры Intel от 8086 до Pentium II. СПб.: Питер, 1997.
Нортон П., Соухэ Д. Язык ассемблера для IBM PC. М.: Компьютер, 1992.
Высокие интеллектуальные технологии образования и науки: Материалы Х Международной научно-методической конференции. 28 февраля - 1 марта 2003 года. Санкт-Петербург. - СПб.: Изд-во СПбГПУ, 2003.– 420 с.
Новые информационные технологии: Учеб. Пособие /Под ред. В.П. Дьяконова; Смол. гос. пед. ун-т. - Смоленск. 2003. - Ч. 3: Основы математики и математическое моделирование / В.П. Дьяконов, И.В. Абраменкова, А.А. Пеньков. - 192 с.: ил.
Дьяконов В. П. Компьютерная математика. Теория и практика. /В. П. Дьяконов. - М.: Нолидж, 2001.
Говорухин В. Н., Цибулин В. Г. Компьютер в математическом исследовании. \ Учебный курс. - СПб.: Питер, 2001.
Айламазян А. К., Информатика и теория развития. - М.: Наука, 1992.
Информатика и образование, \N5 - 1999.
Грэхем Р., Кнут Д., Паташник О. Конкретная информатика. - М.: Мир, 1988.
|
 Скачать 163 Kb.
Скачать 163 Kb.


