СИАОД-1. отправил. Приобретение практических навыков по определению сложности алгоритмов на теоретическом и практическом уровнях

• Название: Приобретение практических навыков по определению сложности алгоритмов на теоретическом и практическом уровнях
• Анкор: СИАОД-1
• Дата: 31.03.2023
• Размер: 427.3 Kb.
• Имя файла: отправил.docx
• Тип: Документы; #1028017

• Цель работы

Приобретение практических навыков по определению

• сложности алгоритмов на теоретическом и практическом уровнях

• 
  эффективного алгоритма решения задачи из нескольких алгоритмов
  

• ЗАДАНИЕ 1

1.1 Формулировка задачи

Выбрать эффективный алгоритм вычислительной задачи из двух предложенных, используя теоретическую и практическую оценку вычислительной сложности каждого из алгоритмов, а также его ёмкостную сложность. Вычислительная задача: дан массив x из n элементов целого типа; удалить из этого массива все значения равные заданному (ключевому) key.

1.2 Модель решения

a) Первый алгоритм работает по следующему образу: проходит по массиву чисел слева вправо, если находит значение, которое нужно удалить, происходит сдвиг последующих значений влево, путём замены значения символа на значение правого от него стоящего. Тем самым массив уменьшается и сдвигается влево. Блок - схема для первого алгоритма рис 1.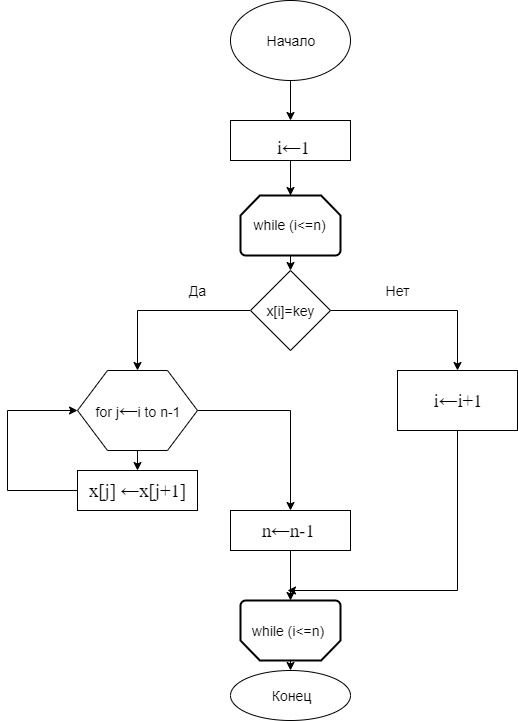



Рисунок 1 – Блок- схема первого алгоритма
Второй алгоритм работает по следующему образу: проходит по массиву параллельно присваивая значение элемента массива значение другому элементу в зависимости от счётчика элементов, который указывает на номер элемента, который равен удаляемому числу. Блок-схема для второго алгоритма рис 2.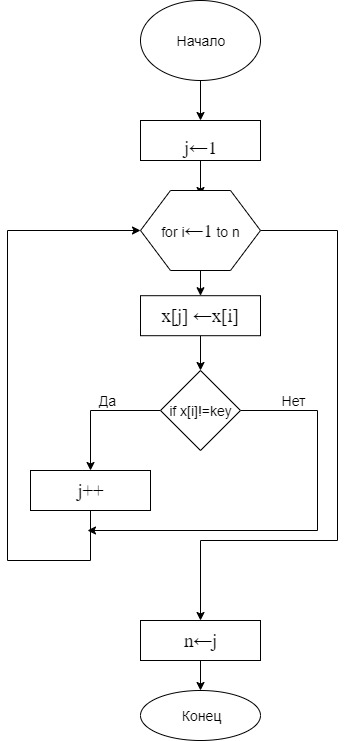



Рисунок 2 – блок схема для второго алгоритма
b) Инвариант первого алгоритма можно определить “i<=n”, где n – кол-во элементов массива

1. Инвариант цикла справедлив до работы цикла.

2. Инвариант цикла справедлив после итерации.

3. Инвариант цикла справедлив по завершению цикла.

4.Цикл завершится, когда условие i<=n перестанет выполнятся.


Инвариантом второго цикла является “i<=n”, где n – кол-во элементов массива.

1. Инвариант цикла справедлив до работы цикла.

2. Инвариант цикла справедлив после итерации.

3. Инвариант цикла справедлив по завершению цикла.

4.Цикл завершится когда i достигнет значения n-1.

c) Определение вычислительной сложности:

Алгоритм №1

Оператор	Кол-во выполнений оператора в строке
	в лучшем случае	в худшем случае
delFirstMetod(x,n,key){
i←1	1	1
while (i<=n) do	n+1	n+1
if x[i]=key then	n	n
//удаление
for j←i to n-1 do	0	n2
x[j] ←x[j+1]	0	n2
od
n←n-1	0	n
else
i←i+1	n	n
endif od }

T₁(n)= 1+n+1+n+n=2+3n

T₂(n)=1+n+1+n+n²+n²+n =2+3n+2n²

Средний случай T(n): 2+3n<=T(n)<=2+3n+2n²
Алгоритм №2

Оператор	Кол-во выполнений оператора в строке
	в лучшем случае	в худшем случае
delOtherMetod(x,n,key){
j←1	1	1
for j←1 to n do	n+1	n+1
x[j] ←x[i]	n	n
if x[i]!=key then	n	n
j++	0	n
endif
od
n←j	1	1
}

T₁(n) = 1+n+1+n+n+1= 3+3n

T₂(n) = 1+n+1+n+n+n+1=3+4n

Средний случай T(n): 3+3n<=T(n)<=3+4n

1.3 Реализация алгоритма в виде функции и его отладка на массиве.

Включим в функцию операторы, подсчитывающие число выполненных сравнений (a) и перемещений элементов при удалении (b).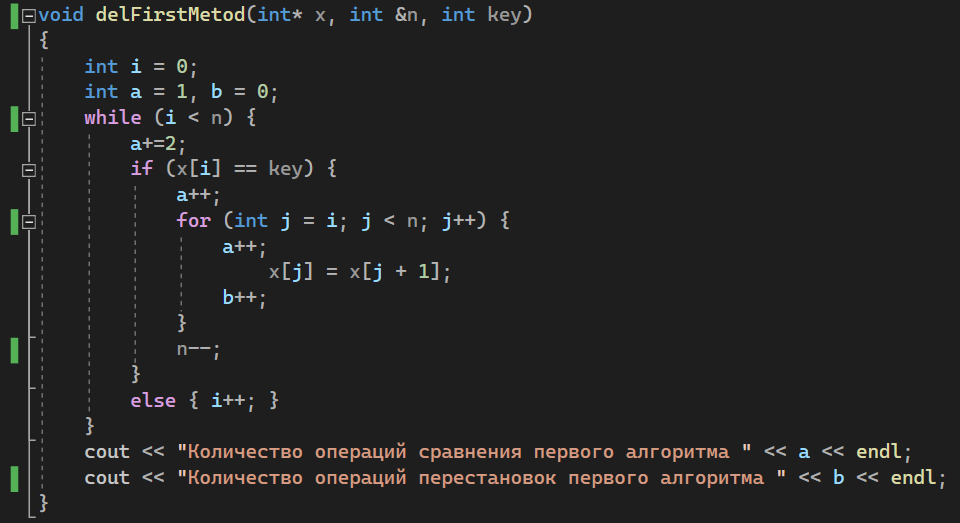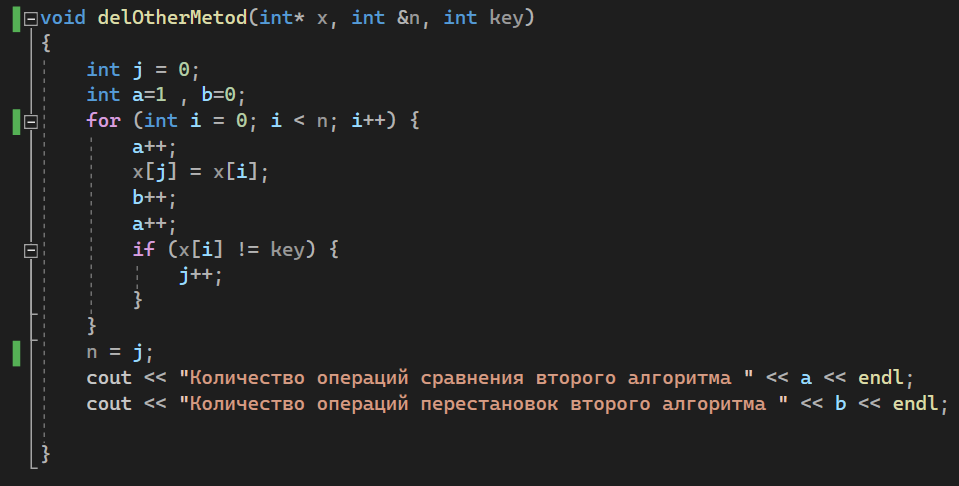




Тестирование при n = 10: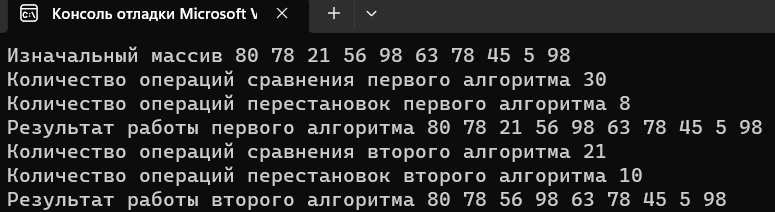



Тестирование при n = 100: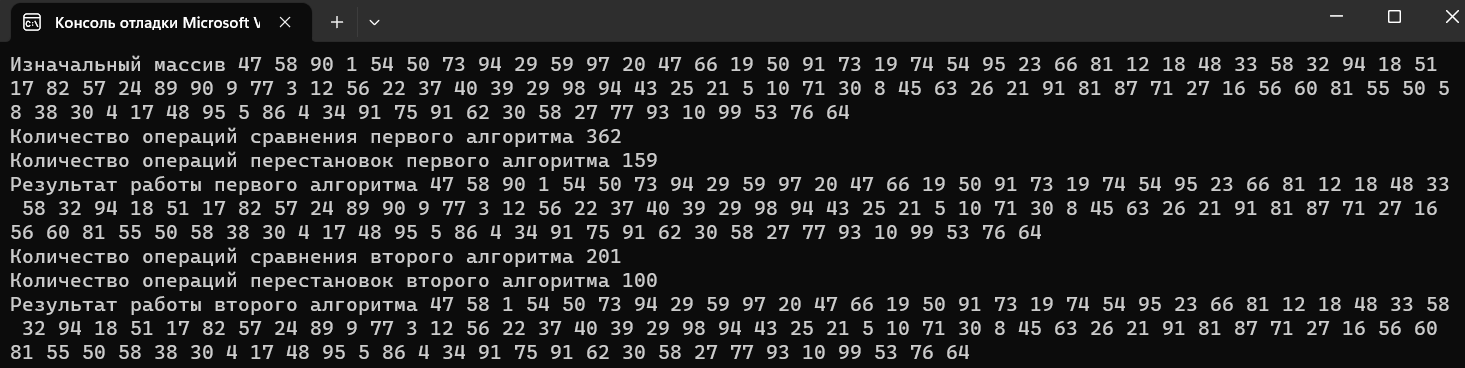


1.4 Реализовать функции: заполнение массива датчиком случайных чисел, вывод массива на экран монитора.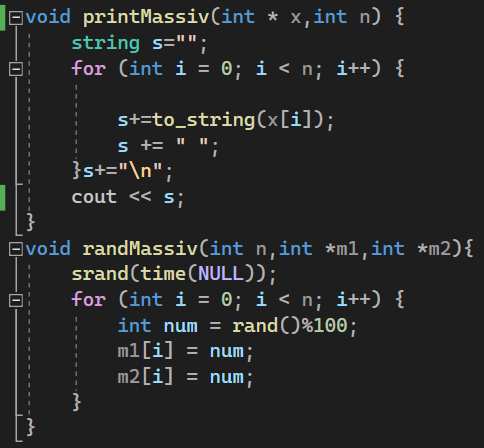 


1.5 Протестировать алгоритм в ситуациях: а) случайное заполнение массива; б) все элементы массива должны быть удалены; в) ни один элемент не удаляется. Сравнить результаты вычислительной сложности этих случаев.

a)Тестирование алгоритма, в случае случайного заполнения массива:



Количество операций первого алгоритма 30+8=38

Количество операций второго алгоритма 21+10=31

б)Тестирование алгоритма, в случае удаления всех элементов массива: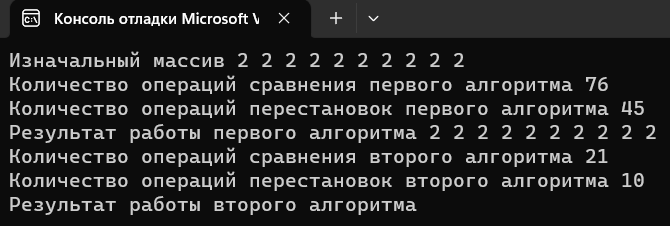



Количество операций первого алгоритма 76+45=121

Количество операций второго алгоритма 21+10=31

в)Тестирование алгоритма, в случае, когда ни один элемент не удаляется: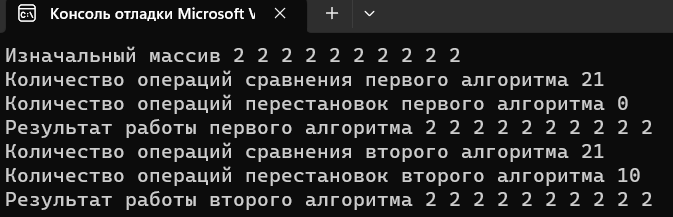



Количество операций первого алгоритма 21+0=21

Количество операций второго алгоритма 21+10=31

Результаты вычислений

	Теоретически для первого алгоритма	Практически для первого алгоритма	Теоретически для второго алгоритма	Практически для второго алгоритма
В лучшем случае	2+3n	38	3n+3	31
В худшем случае	2+3n+2n2	121	4n+3	31
В среднем случае	0<=T(n)<=2n2	21	0<=T(n)<=n	31

ЗАДАНИЕ 2

1. 
   Постановка задачи
   

Получение матрицы обратной данной матрице

2. 
   Модель решения
   

Создаем двумерный массив и наполняем его значениями. Далее проверяем его, чтобы A[i][j] != A[j][i]. Если же A[i][j] != A[j][i], то увеличиваем счетчик k на единицу. В случае, если после проверки всего массива k = 0, то матрица симметрична, в другом же случае – нет.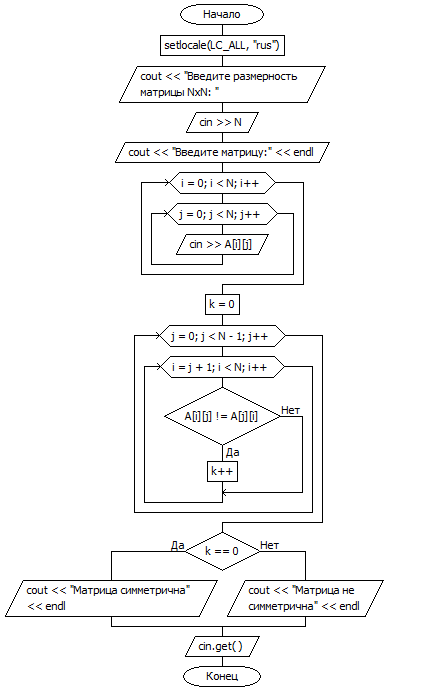



Рисунок 1 – Блок - схема алгоритма

3. 
   Разработка эффективного алгоритма
   

а) Данный алгоритм прогоняется дважды по массиву, первый раз заполняя его нужными значениями, а второй раз проверяя, является ли элемент i строчки j столбца равным элементу j строчки i столбца.

б) Инвариант алгоритма можно определить “i
в) 1. Инвариант цикла справедлив до работы цикла.

2. Инвариант цикла справедлив после итерации.

3. Инвариант цикла справедлив по завершению цикла.
г) Определение вычислительной сложности:

Оператор	Кол-во выполнений оператора в строке (худший случай)	Кол-во выполнений оператора в строке (лучший случай)
void second (int N) {
int A[N][N], k;	1	1
for (int i = 0; i < N; i++)	N+1	N+1
for (int j = 0; j < N; j++)	N2	0
cin >> A[i][j];	N2	0
k = 0;	1	1
for (int j = 0; j < N - 1; j++)	N	0
for (int i = j + 1; i < N; i++)	N2	0
if (A[i][j] != A[j][i])	N2	0
k++;	N2	0
if (k == 0)	1	1
cout << "Матрица симметрична" << endl;	1	1
else
cout << "Матрица не симметрична" << endl;	1	1
cin.get();}	1	1

T₁=1+N+1+N²+ N²+1+N+ N²+ N²+ N²+1+1+1+1 = 6+2N+5N²

T₂=1+N+1+1+1+1+1=6+N

4. 
   Реализация алгоритма в виде одной функции (без декомпозиции на другие функции).
   

5. 
   Проведем тестирование алгоритма на матрице размером 10х10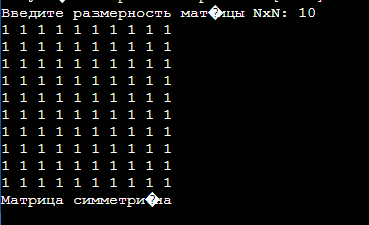
   

6. 
   Выполним практическую оценку сложности алгоритма для лучшего и худшего случаев
   

Лучший случай - это размерность матрицы 0x0:



Худший случай - это любая размерность матрицы, отличная от 0: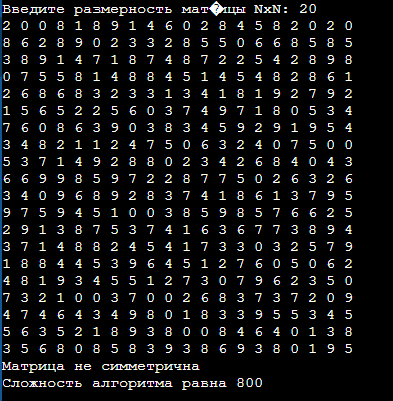



Вывод

ТЕКСТ