Дискретная математика. дискр мат кр1. Приведите к днф булеву функцию f(x, y, z) xy x (y xz) (x (y z) yz)

Название	Приведите к днф булеву функцию f(x, y, z) xy x (y xz) (x (y z) yz)
Анкор	Дискретная математика
Дата	22.03.2022
Размер	134.04 Kb.
Формат файла
Имя файла	дискр мат кр1.docx
Тип	Документы #409229

1

Приведите к ДНФ булеву функцию f(x, y, z) = xy ∨ ¬x (y ∨ xz) ¬(x (y ∨ z) ∨ yz).

f(x, y, z) = ¬(x (¬y ∨ z) ∨ yz)

f(x, y, z) = xy ∨ y¬z

f(x, y, z) = xyz ∨ xy¬z ∨ ¬xy¬z

f(x, y, z) = xy ∨ ¬x (y ∨ xz) ¬(x (y ∨ z) ∨ yz)

Верно

Выберите все верные ответы (может быть несколько или один).

Question2

Сколько минимальных разрезов можно выделить в транспортной сети, содержащей один исток и один сток?

Не более трёх

Один

Равно числу насыщенных дуг в данной сети

Неверно

Выберите все верные ответы (может быть несколько или один).

Question3

Определите периферийные и центральные вершины в графе G по его матрице метрике М (см. таблицу).

М

1

2

3

4

5

6

7

1

0

1

4

5

3

3

2

2

1

0

3

4

2

2

1

3

4

3

0

1

1

2

2

4

5

4

1

0

2

3

3

5

3

2

1

2

0

1

1

6

3

2

2

3

1

0

1

7

2

1

2

3

1

1

0

Периферийные вершины: 1; 3. Центральные вершины: 7; 6

Периферийные вершины: 1; 4. Центральные вершины: 7; 6; 5

Периферийные вершины: 1; 2; 4. Центральные вершины: 7; 6

Верно

Выберите все верные ответы (может быть несколько или один).

Question4

Граф G = (X, U) задан матрицей смежности D.

D

1

2

3

4

5

6

7

8

9

10

1

0

2

2

0

1

0

0

0

0

0

2

2

0

0

0

1

0

0

0

0

0

3

2

0

0

0

0

0

0

0

0

0

4

0

0

0

0

1

0

0

0

0

0

5

1

1

0

1

0

0

0

0

0

0

6

0

0

0

0

0

0

1

1

0

1

7

0

0

0

0

0

1

0

1

0

1

8

0

0

0

0

0

1

1

0

1

0

9

0

0

0

0

0

0

0

1

0

1

10

0

0

0

0

0

1

1

0

1

0

Определите, содержит ли граф G эйлерову цепь.

Не содержит, т.к. есть вершины с нечётными степенями.

Содержит, т.к. есть вершины с нечётными степенями.

Не содержит, т.к. количество вершин с нечётными степенями более двух.

Не содержит, т.к. граф несвязен.

Верно

Выберите все верные ответы (может быть несколько или один).

Question5

Для графа G(X,U),GX,U, где U={(x1x2¯¯¯¯¯¯¯¯¯¯),(x3x4¯¯¯¯¯¯¯¯¯¯),(x3x3¯¯¯¯¯¯¯¯¯¯),(x2x2¯¯¯¯¯¯¯¯¯¯),(x1x3¯¯¯¯¯¯¯¯¯¯),(x1x4¯¯¯¯¯¯¯¯¯¯),(x4x2¯¯¯¯¯¯¯¯¯¯)},U=x1x2¯,x3x4¯,x3x3¯,x2x2¯,x1x3¯,x1x4¯,x4x2¯, по графу его дополнения напишите минимальное выражение произведения ПП логических переменных x1,x2,x3,x4,x1,x2,x3,x4, позволяющее выделить подмножества вершин в графе G,G, образующие все его максимальные полные подграфы.

П=x1x2+x1x2x4+x2x3П=x1x2+x1x2x4+x2x3

П=x1x2+x2x3x4П=x1x2+x2x3x4

П=x3+x2П=x3+x2

Неверно

Выберите все верные ответы (может быть несколько или один).

Question6

На основании таблицы истинности бинарных операций запишите бинарную логическую операцию x₁ | x₂ логической формулой.

¬x₁¬x₂ ∨ ¬x₁x₂ ∨ x₂¬x₁

x₁ & x₂

¬x₁¬x₂ ∨ ¬x₁x₂

Неверно

Выберите все верные ответы (может быть несколько или один).

Question7

Неор. граф G задан матрицей смежности R. Элементы r_ij матрицы смежности R неор. графа G имеют следующие значения:
r₁₈ = 1; r₅₈ = 1; r₁₆ = 1; r₂₈ = 2; r₇₈ = 1; r₇₆ = 1; r₃₆ = 3; r₄₆ = 1; r₃₄ = 1.
Укажите концевые вершины эйлеровой цепи в графе G.

Таких вершин нет, т.к. данный граф не содержит эйлерову цепь

1; 5

8; 5

5; 7

Неверно

Выберите все верные ответы (может быть несколько или один).

Question8

На основании таблицы истинности бинарных операций определите СДНФ операции x₁

x₂.

	x₁ ∨ x₁¬x₂
	x₁x₂ ∨ ¬x₁¬x₂
	¬x₁x₂ ∨ x₁¬x₂

Верно

Выберите все верные ответы (может быть несколько или один).

Question9

На карту Карно (см. рисунок) нанесены значения булевой функции f(x, y).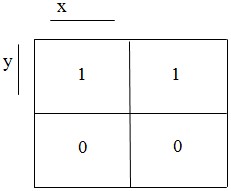

Запишите сокращённую дизъюнктивную нормальную форму булевой функции f(x, y) с помощью карты Карно.

	f(x, y) = y
	f(x, y) = xy ∨ ¬xy
	f(x, y) = (¬x ∨ y)(x ∨ ¬y)
	f(x, y) = xy ∨ ¬yx ∨ ¬x¬y

Неверно

Выберите все верные ответы (может быть несколько или один).

Question10

Для графа G(X,U),GX,U, где U={(x1x2¯¯¯¯¯¯¯¯¯¯),(x3x4¯¯¯¯¯¯¯¯¯¯),(x3x2¯¯¯¯¯¯¯¯¯¯),(x1x3¯¯¯¯¯¯¯¯¯¯)},U=x1x2¯,x3x4¯,x3x2¯,x1x3¯, по графу его дополнения напишите минимальное выражение произведения ПП логических переменных x1,x2,x3,x4,x1,x2,x3,x4, позволяющее выделить подмножества вершин в графе G,G, образующие все его максимальные полные подграфы.

	П=x4+x1x2П=x4+x1x2
	П=x1+x2x3П=x1+x2x3
	П=x1x2+x2x3x4П=x1x2+x2x3x4

Неверно

Выберите все верные ответы (может быть несколько или один).

Question11

На карту Карно (см. рисунок) нанесены значения булевой функции f(x, y).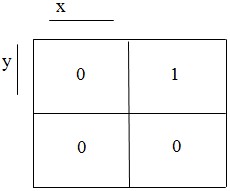

Запишите минимальную конъюнктивную нормальную форму булевой функции с помощью карты Карно.

	f(x, y) = x ∨ y
	f(x, y) = ¬x ∨ ¬y
	f(x, y) = ¬xy

Неверно

Выберите все верные ответы (может быть несколько или один).

Question12

Для графа G=(X,U^),G=X,U^, где U^={(x1x2¯¯¯¯¯¯¯¯¯¯),(x3x4¯¯¯¯¯¯¯¯¯¯),(x1x3¯¯¯¯¯¯¯¯¯¯),(x2x4¯¯¯¯¯¯¯¯¯¯),(x1x4¯¯¯¯¯¯¯¯¯¯),(x3x2¯¯¯¯¯¯¯¯¯¯)},U^=x1x2¯,x3x4¯,x1x3¯,x2x4¯,x1x4¯,x3x2¯, постройте дополнительный граф G¯¯¯¯=(X',U'^).G¯=X',U'^.
Ответ запишите в виде последовательности рёбер множества U'^.U'^.

	U'^=(x1x2¯¯¯¯¯¯¯¯¯¯),(x3x4¯¯¯¯¯¯¯¯¯¯),(x1x3¯¯¯¯¯¯¯¯¯¯),(x2x4¯¯¯¯¯¯¯¯¯¯)U'^=x1x2¯,x3x4¯,x1x3¯,x2x4¯
	U'^=(x1x2¯¯¯¯¯¯¯¯¯¯),(x3x4¯¯¯¯¯¯¯¯¯¯),(x1x3¯¯¯¯¯¯¯¯¯¯),(x2x4¯¯¯¯¯¯¯¯¯¯),(x2x4¯¯¯¯¯¯¯¯¯¯),(x1x4¯¯¯¯¯¯¯¯¯¯)U'^=x1x2¯,x3x4¯,x1x3¯,x2x4¯,x2x4¯,x1x4¯
	U'^=∅U'^=∅

Неверно

Выберите все верные ответы (может быть несколько или один).

Question13

Определите, когда логическая функция
f(x₁, x₂, x₃) = (x₁ ¬x₂) → ((x₁ ∨ x₃) & x₂)
будет принимать значение «0».

	Если (x₁ ¬x₂) = 0, а ((x₁ ∨ x₃) & x₂) = 1
	Если (x₁ ¬x₂) = 1, а ((x₁ ∨ x₃) & x₂) = 0
	Никогда
	Всегда

Верно

Выберите все верные ответы (может быть несколько или один).

Question14

Для графа G(X,U),GX,U, где U={(x1x2¯¯¯¯¯¯¯¯¯¯),(x3x4¯¯¯¯¯¯¯¯¯¯),(x3x2¯¯¯¯¯¯¯¯¯¯),(x1x3¯¯¯¯¯¯¯¯¯¯),(x1x4¯¯¯¯¯¯¯¯¯¯)},U=x1x2¯,x3x4¯,x3x2¯,x1x3¯,x1x4¯, по графу его дополнения напишите минимальное выражение произведения ПП логических переменных x1,x2,x3,x4,x1,x2,x3,x4, позволяющее выделить подмножества вершин в графе G,G, образующие все его максимальные полные подграфы.

	П=x2+x3П=x2+x3
	П=x1+x4П=x1+x4
	П=x4+x2П=x4+x2

Неверно

Выберите все верные ответы (может быть несколько или один).

Question15

Решите задачу с помощью диаграмм Эйлера–Венна (см. рисунок).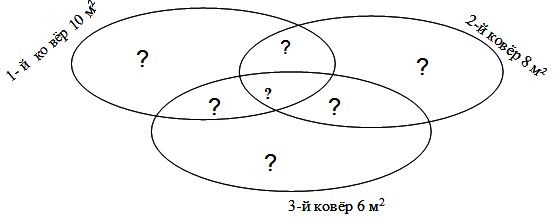

На полу комнаты площадью 24 м² лежат три ковра. Площадь одного из них – 10 м², другого – 8 м², третьего – 6 м². Каждые два ковра перекрываются по площади 3 м², а площадь участка пола, покрытого всеми тремя коврами, составляет 1 м². Найдите площадь участка пола:
а) покрытого первым и вторым коврами, но не покрытого третьим ковром;
б) покрытого только первым ковром;
в) непокрытого коврами.

	а) 3 м²; б) 5 м²; в) 1 м²
	а) 10 м²; б) 5 м²; в) 8 м²
	а) 10 м²; б) 5 м²; в) 6 м²

Верно

Выберите все верные ответы (может быть несколько или один).

Question16

Сравните множества М1 и М2, где М1 = {2, 23, 3, 15, 1, 2, 18, 9, 9}; M2 = {9, 18, 2, 1, 15, 3, 23, 2}.

	М1 > М2
	М1 < М2
	М1 = М2
	М1 ≠ М2

Неверно

Выберите все верные ответы (может быть несколько или один).

Question17

Универсальное множество I включает целые числа: 1, 2, …, 100. Множество М = {35, 12, 34, 56}. Определите элементы множества I ∩ M.

	I ∩ M = {1, 2, …, 100}
	I ∩ M = {35, 12, 34, 56}
	I ∩ M = ∅

Неверно

Выберите все верные ответы (может быть несколько или один).

Question18

1) Раскрасьте вершины графа G=(X,U),G=X,U, применяя метод Магу–Вейсмана, если U={(x1x2¯¯¯¯¯¯¯¯¯¯),(x3x4¯¯¯¯¯¯¯¯¯¯),(x2x3¯¯¯¯¯¯¯¯¯¯),(x4x5¯¯¯¯¯¯¯¯¯¯),(x2x6¯¯¯¯¯¯¯¯¯¯),(x5x6¯¯¯¯¯¯¯¯¯¯),(x6x7¯¯¯¯¯¯¯¯¯¯)}.U=x1x2¯,x3x4¯,x2x3¯,x4x5¯,x2x6¯,x5x6¯,x6x7¯.
2) Определите хроматическое число γ(G).γG.
3) Выделите множества вершин K(G),KG, которым можно приписать одно и тоже натуральное число или цвет.

	γ(G)=3;K(G)={x2;x4x6;x1x3x5x7};{x6;x2x4;x1x3x5x7}γG=3;KG=x2;x4x6;x1x3x5x7;x6;x2x4;x1x3x5x7
	γ(G)=2;K(G)={x4x6;x1x3x5x7};{x2x4;x1x3x5x7}γG=2;KG=x4x6;x1x3x5x7;x2x4;x1x3x5x7
	γ(G)=2;K(G)={x2;x4x6;x1x3x5x7};{x6;x2x4;x1x3x5x7}γG=2;KG=x2;x4x6;x1x3x5x7;x6;x2x4;x1x3x5x7

Неверно

Выберите все верные ответы (может быть несколько или один).

Question19

Множество М = М1 ∩ М2, где М1 = {2, 23, 3, 15, 18, 9, 9}; M2 = {5, 6, 1, 16, 15, 32, 45, 2}. Определите элементы множества М.

	М = {2, 23, 3, 15, 18, 9, 9}
	М = {15, 2}
	М = {2, 23, 3, 15, 18, 9, 9, 5, 6, 1, 16, 15, 32, 45, 2}

Неверно

Выберите все верные ответы (может быть несколько или один).

Question20

Определите, относится ли граф G(X,U^),GX,U^, где U^={(x1x2¯¯¯¯¯¯¯¯¯¯),(x3x4¯¯¯¯¯¯¯¯¯¯),(x1x3¯¯¯¯¯¯¯¯¯¯),(x2x4¯¯¯¯¯¯¯¯¯¯),(x1x4¯¯¯¯¯¯¯¯¯¯),(x1x1¯¯¯¯¯¯¯¯¯¯),(x3x2¯¯¯¯¯¯¯¯¯¯)},U^=x1x2¯,x3x4¯,x1x3¯,x2x4¯,x1x4¯,x1x1¯,x3x2¯, к классу обыкновенных графов.

	Относится
	Не относится
	Относится к классу смешанных графов

Неверно

Выберите все верные ответы (может быть несколько или один).