Основы проектирования машин Привод транспортера. КР №1 Детали машин для сайта. Привод транспортера
 Скачать 247.81 Kb. Скачать 247.81 Kb.
|
|
Федеральное агентство по образованию РФ ФГФОУ ВПО Уральский федеральный университет имени первого Президента России Б.Н.Ельцина Кафедра «МирМ» Проект по модулю Основы проектирования машин: ПРИВОД ТРАНСПОРТЕРА Руководитель: Реков А. М. доцент, к.т.н. Студент группы Екатеринбург 2020 ЗАДАНИЕ № 1(2020) На практические занятия по курсу "Механика" для студентов Группы НМТЗ 193140д уТ Привод ленточного транспортера 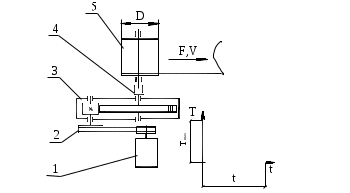 1) двигатель; 2) клиноременная передача; 3) редуктор горизонтальный цилиндрический прямозубый; 4)муфта зубчатая; 5) барабан конвейера. На схеме приведен график изменения нагрузки на конвейер. Скорость ленты – постоянная. Рис1. Таблица 1 Исходные данные
1. Выбор электродвигателя и расчет основных параметров привода1.1. Выбор электродвигателя. 1.1.1 Требуемая мощность электродвигателя 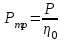 где 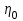 - общий КПД привода - общий КПД привода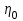 = =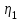 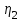 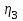 2= 2= 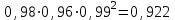 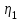 = 0,98 - КПД зубчатой передачи, = 0,98 - КПД зубчатой передачи, 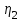 = 0,96 - КПД ременной передачи, = 0,96 - КПД ременной передачи,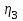 = 0,99 - КПД одной пары подшипников качения, согласно [табл. П2] = 0,99 - КПД одной пары подшипников качения, согласно [табл. П2]Тогда 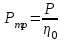 = = 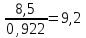 кВт. кВт.Синхронную частоту вращения двигателя выбираем из диапазона nc= (5…10) n2= (5…10) *130=650…1300 По требуемой мощности из работы [ табл. П1 ] приложения выбираем электродвигатель 4А160S6 с ближайшей большей стандартной мощностью 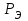 = 11 кВт, синхронной частотой вращения nc = 1000 мин-1 и скольжением S=2,7 % = 11 кВт, синхронной частотой вращения nc = 1000 мин-1 и скольжением S=2,7 %1.1.2 Частота вращения вала двигателя 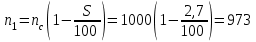 мин-1 мин-11.1.3 Общее передаточное число привода 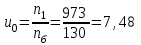 1.1.4 Передаточное число зубчатой передачи Принимаем для зубчатой передачи стандартное значение передаточного числа 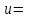 3,15 3,15 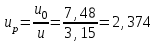 Полученное значение 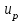 округляют до ближайшего стандартного из округляют до ближайшего стандартного из [табл. 7.1]. Принимаем 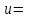 2,5. 2,5.1.2 Частоты вращения валов (индекс соответствует номеру вала на схеме привода): 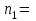 973 мин-0 973 мин-0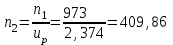 мин-1 мин-1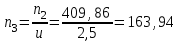 мин-1 мин-11.3 Мощности, передаваемые валами: P1=Pтр= 9,2 кВт P2=P1 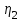 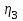 = 9,2*0,96*0,99 = 8,7 кВт = 9,2*0,96*0,99 = 8,7 кВтP3=P2 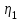 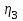 = 8,7*0,98*0,99 = 8,4 кВт = 8,7*0,98*0,99 = 8,4 кВт1.4. Крутящие моменты, передаваемые валами. Крутящий момент на валу определяется по формуле 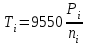 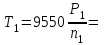 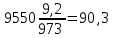 Н м Н м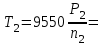 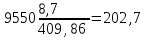 Н м Н м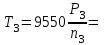 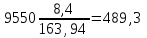 Н м Н мУточненный расчет зубчатой передачи с моментом 202,7 Нм 2. Расчет зубчатой передачи 2.1. Выбор материалов зубчатых колес Определяем размеры характерных сечений заготовок по формулам, принимая, что при передаточном числе зубчатой передачи u> 4 шестерня изготавливается за одно целое с валом. 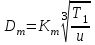 . Для прямозубой передачи . Для прямозубой передачи 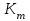 =24. Тогда =24. Тогда 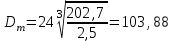 мм. мм.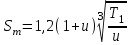 =1,2*(1+2,5) * =1,2*(1+2,5) *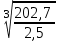 = 18,18 мм. = 18,18 мм.Диаметр заготовки для колеса равен 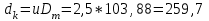 мм. мм.Выбираем материал для колеса и шестерни - сталь 40 ХН, термообработка - улучшение, твердость поверхности зуба шестерни – 235…262 НВ, 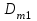 = 315 мм, = 315 мм, 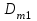 > >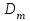 , твердость поверхности зуба колеса – 269…302 HB, Sm1>Sm. [табл. 1.1]. , твердость поверхности зуба колеса – 269…302 HB, Sm1>Sm. [табл. 1.1].Определяем средние значения твердости поверхности зуба шестерни и колеса: НВ1 = 0,5(НB1min+ НВ1max) = 0,5(235+262) = 248,5; НВ2 = 0,5(НB2min+ НВ2max) = 0,5(269+302) =285,5. 2.1. Определение допускаемых напряжений 2.1.1. Допускаемые контактные напряжения Допускаемые контактные напряжениия определяем по зависимости 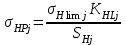 где индекс j=1 соответствует шестерне, а индекс j=2 –колесу. Пределы контактной выносливости определим по формулам: 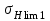 =2НВ1+70=2*248,5+70 = 567 МПа, =2НВ1+70=2*248,5+70 = 567 МПа,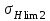 =2HВ2+70=2*285,5+70 = 641 МПа . =2HВ2+70=2*285,5+70 = 641 МПа .Коэффициенты безопасности одинаковы для шестерни и колеса 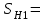 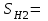 1,1 (в соответствии с материалом и термообработкой). [табл. 2.1] 1,1 (в соответствии с материалом и термообработкой). [табл. 2.1]Коэффициенты долговечности 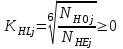 Базовые числа циклов при действии контактных напряжений 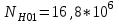 ; ;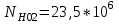 . [табл. 1.1] . [табл. 1.1]Эквивалентные числа циклов напряжений 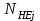 = =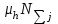 , ,где 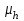 = 0.5 - коэффициент эквивалентности для тяжелого режима работы. = 0.5 - коэффициент эквивалентности для тяжелого режима работы.Суммарное число циклов нагружения 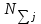 =60njcth, =60njcth,где с =1, th - суммарное время работы передачи, th = 365 L 24 kгkc ПВ. Здесь ПВ=0,00ПВ%=0,01*40 =0,40. В результате расчетов получим th =365*5*24*0,8*0,45*0,4 = 6307 ч, 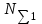 =60*973*6307=3,68*108, =60*973*6307=3,68*108, 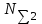 =60*409,86*6307=1,55*108 об. =60*409,86*6307=1,55*108 об.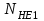 =0,5 *3,68*108=184*106; =0,5 *3,68*108=184*106;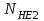 = 0,5*1,55*106=77,5*106 циклов. = 0,5*1,55*106=77,5*106 циклов.Значение коэффициента долговечности KHL определяется по формуле 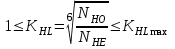 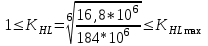 . Принимаем . Принимаем 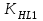 =0,99. =0,99.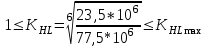 . Принимаем . Принимаем 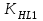 =0,82. =0,82.Определим допускаемые контактные напряжения для шестерни и колеса: 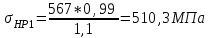 ; ;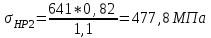 , ,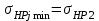 Допускаемые контактные напряжения для прямозубой передачи 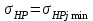 = 477,8 МПа. = 477,8 МПа.2.1.2 Допускаемые напряжения изгиба Допускаемые напряжения изгиба вычисляем по формуле 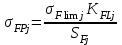 Пределы изгибной выносливости зубьев 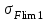 = 1,75*НВ1=1.75*248.5= 434,9 МПа, = 1,75*НВ1=1.75*248.5= 434,9 МПа,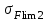 = 1,75*HB2=1.75*285.5= 499,6 МПа. = 1,75*HB2=1.75*285.5= 499,6 МПа.Коэффициенты безопасности при изгибе: SF1=1,7; SF2=1,7 (в соответствии с материалом и термообработкой). Коэффициенты, учитывающие влияние двухстороннего приложения нагрузки, для нереверсивного привода КFC1=1, КFC2=1 Коэффициенты долговечности 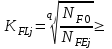 0, 0,где qj - показатель степени кривой усталости, q1=6, q2=6 [табл. 3.1]; NF0 = 4*106 - базовое число циклов при изгибе. Эквивалентное число циклов напряжений при изгибе NFEj= 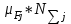 , , где 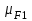 = 0,3, = 0,3, 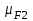 =0,3 - коэффициенты эквивалентности для тяжелого режима работы. =0,3 - коэффициенты эквивалентности для тяжелого режима работы.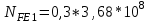 =110,4*106; =110,4*106;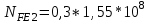 =46,5*106 =46,5*106Поскольку 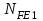 > NF0, примем КFL1 = 1. Вычислим КFL2 = > NF0, примем КFL1 = 1. Вычислим КFL2 = 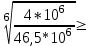 = 0,66. = 0,66.Определим допускаемые напряжения изгиба для шестерни и колеса: 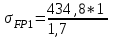 = 255,8 МПа; = 255,8 МПа;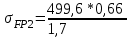 = 194 МПа = 194 МПа2.2. Проектный расчет передачи 2.2.1 Межосевое расстояние 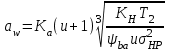 где 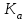 =450 для прямозубых передач [1]. =450 для прямозубых передач [1].Коэффициент ширины зубчатого венца принимаем 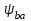 = 0,4. На этапе проектного расчета задаемся значением коэффициента контактной нагрузки Кн= 1,2. Тогда = 0,4. На этапе проектного расчета задаемся значением коэффициента контактной нагрузки Кн= 1,2. Тогда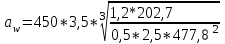 = 149 мм. = 149 мм.Полученное межосевое расстояние округлим до ближайшего большего стандартного значения 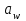 = 160 мм. = 160 мм.2.2.2 Модуль, числа зубьев колес и коэффициенты смещения Рекомендуемый диапазон для выбора модуля m= (0,01…0,02) * 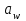 = (0,01…0,02) *160 = 1,6…3,2 мм. = (0,01…0,02) *160 = 1,6…3,2 мм. Из полученного диапазона выберем стандартный модуль m = 2,5 мм. Суммарное число зубьев передачи 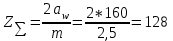 . .Число зубьев шестерни 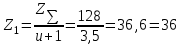 . .Число зубьев колеса 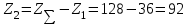 . .Фактическое передаточное число uф = 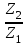 = = 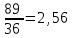 . .При 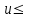 2,5 отличие фактического передаточного числа от номинального должно быть не больше 2,5 %. 2,5 отличие фактического передаточного числа от номинального должно быть не больше 2,5 %.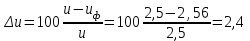 % %Учитывая, что Z0>17, принимаем коэффициенты смещения x1=0, х2 =0. Ширина зубчатых венцов и диаметры колес Ширину зубчатого венца колеса определим по формуле bw2= 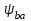 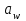 =0,5*160= 80 мм. =0,5*160= 80 мм.Округлим bw2 до ближайшего числа из ряда нормальных линейных размеров bw2= 80 мм. Ширину зубчатого венца шестерни bw1 принимают на 2...5 мм больше, чем bw2. Примем bw1=85 мм. Диаметры окружностей зубчатых колес: делительные окружности dj=mZj d1=mZ1=2,5*36=90 мм, d2=mZ2 = 2,5*92 = 230 мм, окружности всршин зубьев daj= dj +2m(1+xj), da1= 90 +2*2,5*1= 95 мм, da2= 230 +2*2,5*1= 235 мм, окружности впадин зубьев dfj= dj -2m(1,25-xj), df1=90 – 2*2,5*1,25 = 83,75 мм, df2=230 - 2*2,5*1,25 = 223,75 мм. 2.2.3. Окружная скорость в зацеплении и степень точности передачи Величину окружной скорости передачи рассчитываем по зависимости 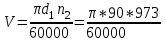 =4,6 м/с. =4,6 м/с.Для полученной скорости назначим степень точности передачи nст=8 [ табл.8.1 ] 3. Проверочный расчет передачи 3.1 Проверка контактной прочности зубьев. 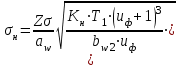 , , 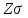 =9600 для прямозубых передач =9600 для прямозубых передачКоэффициент контактной нагрузки Кн =Кна*Кнв*Кнv Коэффициент неравномерности распределения нагрузки между зубьями 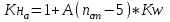 , ,где А=0,06 для прямозубых передач 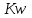 - коэффициент, учитывающий приработку зубьев. - коэффициент, учитывающий приработку зубьев.При 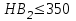 для определения для определения 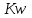 используют выражение используют выражение 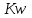 = 0,002* = 0,002*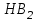 + 0,036(V-9) =0,002*285,5+0,036(4,6-9) =0,413 + 0,036(V-9) =0,002*285,5+0,036(4,6-9) =0,413Тогда 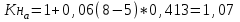 Коэффициент неравномерности распределения нагрузки по ширине колеса 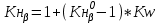 , ,где 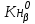 - коэффициент неравномерности распределения нагрузки в начальный период работы. - коэффициент неравномерности распределения нагрузки в начальный период работы.Для определения 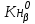 вычислим коэффициент ширины венца по диаметру вычислим коэффициент ширины венца по диаметру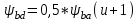 По значению 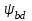 определим определим 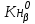 методом линейной интерполяции методом линейной интерполяции(см. табл.9.1) 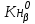 =1,03. Тогда =1,03. Тогда 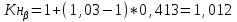 Динамический коэффициент определим методом линейной интерполяции по (табл. 10.1)  Кнv=1,15 Кнv=1,15Окончательно найдем Кн и 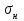 : :Кн = 1,07*1,012*1,15=1,25  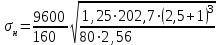 = 432 МПа = 432 МПаПоскольку 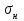 < <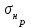 (432>477.8) выполним расчет недогруза по контактным напряжениям (432>477.8) выполним расчет недогруза по контактным напряжениям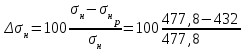 =9,6 % <15 % =9,6 % <15 %3.2 Проверка изгибной прочности зубьев. Напряжение изгиба в зубе шестерни 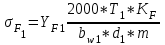 Коэффициент формы зуба при хj=0 равен 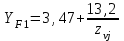 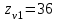 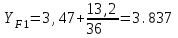 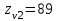 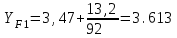 Коэффициент нагрузки при изгибе КF =КFa*КFв *КFv КFa =1 для прямозубых передач КFв =0,18+0,82* 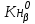 = 0,18+0,82*1,03=1,025 = 0,18+0,82*1,03=1,025КFv = 1+1,5(Кнv-1) при НВ2 <350 КFv = 1+1,5(1,15-1) =1,225 КF =1*1,025 *1,225=1,256 Тогда 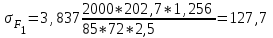 МПа < МПа <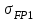 (293,88 МПа) (293,88 МПа)Напряжение изгиба в зубьях колеса 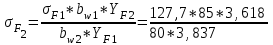 =127,9 МПа < =127,9 МПа <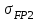 (168,84 МПа) (168,84 МПа)3.3 Силы в зацеплении Окружная сила 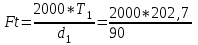 = 4504 Н = 4504 НРаспорная сила 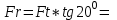 4504*0,364=1639,6 Н 4504*0,364=1639,6 Н4. Расчет клиноременной передачи 1. Определение крутящего момента на ведущем шкиве и выбор ремня: 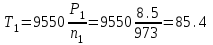 Н*м Н*мПо величине крутящего момента на ведущем шкиве выбираем ремень со следующими параметрами (табл. 1.3): тип сечения – поперечное сечение клинового ремня; площадь поперечного сечения A= 138 мм2; ширина нейтрального слоя bp= 14 мм; масса погонного метра ремня qm=0,18 кг/м. 2. Диаметры шкивов Диаметр ведущего шкива определим по формуле: d1=40 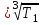 = 40 = 40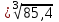 =176 =176Округлим d1 до ближайшего значения из ряда на с. 77: d1= 180 мм. Диаметр ведомого шкива равен: d2=u 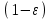 d1=2*(1-0,015) *180=354,6 d1=2*(1-0,015) *180=354,6После округления получим: d2= 355 мм. 3. Фактическое передаточное число uф= 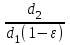 = =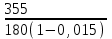 = 2 = 24. Предварительное значение межосевого расстояния 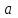 = 0.8 (d1+d2) = 0,8(180+355) =428 мм = 0.8 (d1+d2) = 0,8(180+355) =428 мм5. Длина ремня L=2 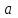 +0.5 +0.5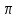 (d1+d2)+ (d1+d2)+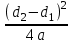 = ==2*428+0,5*3,14(180+355) + 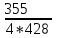 =1714,3 мм =1714,3 ммОкруглим до ближайшего числа из ряда на: L= 1600 мм. После выбора Lуточняем межосевое расстояние 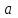 = 0.25(L-W+ = 0.25(L-W+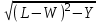 )=0,25(1600-840+ )=0,25(1600-840+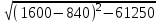 = 369,6 мм = 369,6 ммгде W = 0.5 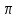 (d1+d2) =0,5*3,14(180+355) = 840 мм (d1+d2) =0,5*3,14(180+355) = 840 мм Y = 2 (d2- d1)2=2*(355-180)2 = 61250 мм 6. Угол обхвата на ведущем шкиве 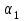 = =  -57. -57.  = =  -57. -57.  = =  7. Скорость ремня V=  = =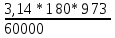 =9,17 м/с =9,17 м/с8. Окружное усилие равно Ft= 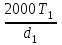 = =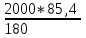 =948,9 Н =948,9 Н9. Частота пробегов ремня 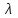 = =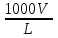 = = 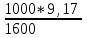 =5,731 с-1 =5,731 с-110. Коэффициент, учитывающий влияние передаточного числа на напряжения изгиба в ремне, Cu=1.14- 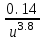 =1,14- =1,14-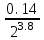 =1,13 =1,1311. Приведенное полезное напряжение для ремней нормального сечения 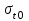 = = 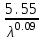 - -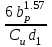 -0.001V2= -0.001V2= 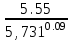 - -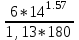 -0.001*9,172=2,8 МПа -0.001*9,172=2,8 МПа12. Допускаемое полезное напряжение [ 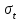 ] = ] =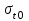 C C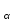 Cp=2,8*0,93*0,8=2,08 МПа Cp=2,8*0,93*0,8=2,08 МПагде C 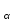 - коэффициент, учитывающий влияние угла обхвата, - коэффициент, учитывающий влияние угла обхвата,C 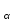 = 1-0.44 ln = 1-0.44 ln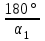 =1-0.44 ln =1-0.44 ln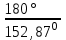 =0,93 =0,93Cp - коэффициент режима работы. Cp = Cн-0.1(nc-1) =1-0,1(3-1) =0,8 nc- число смен работы передачи в течении суток; nc =3 Cн- коэффициент нагружения при постоянной нагрузке, Cн=1 13. Расчетное число ремней Z= 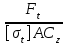 = =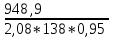 =3,58 =3,58где Сz - коэффициент, учитывающий неравномерность распределения нагрузки между ремнями (табл. 3.3 [1]), предварительно приняли Сz=0,95. Расчетное значение Z округлим до ближайшего большего целого числа Z=4 14. Сила предварительного натяжения одного ремня S0 = 0.75 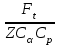 + qmV2=0,75 + qmV2=0,75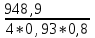 + 0,18*9,17 2= 254,3 Н + 0,18*9,17 2= 254,3 Н15. Сила, нагружающая валы передачи, Fb = 2 S0 Z sin 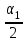 =2*254,3* 4sin =2*254,3* 4sin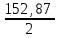 = 1977,3 Н = 1977,3 НБиблиографический список 1. Баранов Г.Л. Расчет деталей машин: учебное пособие/ Г.Л. Баранов. Екатеринбург: УГТУ–УПИ, 2007. |
