Экзаменационные билеты. экз.билеты 10 класс теория. Признак перпендикулярности двух плоскостей и следствие из него
 Скачать 31 Kb. Скачать 31 Kb.
|
|
Билет №1 Признак перпендикулярности двух плоскостей и следствие из него. Формулы сложения тригонометрических функций. Найти сумму бесконечно убывающей геометрической прогрессии 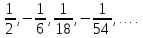 Билет № 2 Взаимное расположение прямых в пространстве. Признак скрещивающихся прямых. Показательная функция, её свойства и график. Решить уравнение 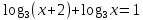 . .Билет № 3 Определение параллельных плоскостей. Признак параллельности двух плоскостей. Логарифм. Свойства логарифмов. Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС = 13 см, ВС = 10 см, ребро АD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды. Билет № 4 Теорема о прямой, перпендикулярной к плоскости. Десятичные и натуральные логарифмы. Формула перехода к новому основанию. Изобразите тетраэдр KLMN. Постройте сечение этого тетраэдра плоскостью, проходящей через ребро KLи середину А ребра MN. Билет № 5 Определение параллельных прямых в пространстве. Теорема о параллельных прямых. Параллельность трёх прямых. Логарифмическая функция, её свойства и график. Вычислить 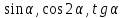 , если , если 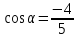 и и 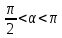 . .Билет № 6 Признак параллельности прямой и плоскости. Свойство плоскости, проходящей через прямую, параллельную другой плоскости. Свойства двух параллельных прямых и плоскости. Определение синуса, косинуса и тангенса угла. Построить график функции  и указать область определения и те значения и указать область определения и те значения 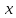 , при которых , при которых 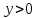 . .Билет № 7 Теорема о трёх перпендикулярах. Обратная теорема. Уравнение  . Арккосинус. . Арккосинус.Решить неравенство 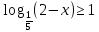 . .Билет № 9 Свойства параллельных плоскостей. Теорема об отрезках параллельных прямых, заключенных между двумя параллельными плоскостями. Уравнение 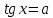 . Арктангенс. . Арктангенс.Через вершину прямого угла С равнобедренного прямоугольного треугольника АВС проведена прямая СМ, перпендикулярная к его плоскости. Найдите расстояние от точки М до прямой АВ, если АС = 4 см, а СМ = 2 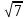 см. см.Билет № 10 Пирамида. Правильная пирамида и её свойства. Уравнение 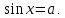 Арксинус. Арксинус.В треугольнике ABCугол С прямой, BC = 8 см, AC= 6 см, CМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника ABC, причем СК = 12 см. Найдите КМ. Доказать тождество 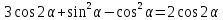 . .Билет № 11 Прямоугольный параллелепипед и его свойства. Формула суммы и разности тригонометрических функций. Решить неравенство 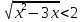 Билет № 12 Признак перпендикулярности прямой и плоскости. Логарифмические уравнения и неравенства. Решить уравнение 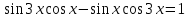 Билет № 13 Прямая, перпендикулярная к плоскости. Связь между параллельностью прямых и их перпендикулярностью к плоскости. Показательные уравнения и неравенства. Упростить выражение 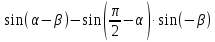 . .Билет № 14 Углы с сонаправленными сторонами. Теорема об углах с сонаправленными сторонами. Угол между прямыми. Бесконечно убывающая геометрическая прогрессия. Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 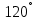 между ними. Наибольшая из площадей боковых граней равна 35 см2. Найдите площадь боковой поверхности призмы. между ними. Наибольшая из площадей боковых граней равна 35 см2. Найдите площадь боковой поверхности призмы.Билет № 15 Аксиомы стереометрии и следствия из них. Арифметический корень натуральной степени. Найти значение выражения 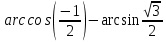 Билет № 16 Перпендикулярные прямые в пространстве. Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Степенная функция, её свойства и график. Билет № 17 Взаимное расположение прямой и плоскости. Параллельность прямой и плоскости. Иррациональные уравнения. Точка К – середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор 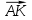 по векторам по векторам 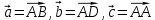 1 и найдите длину этого вектора, если ребро куба равно 1 и найдите длину этого вектора, если ребро куба равно 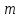 . .Билет № 18 Свойство скрещивающихся прямых и плоскости, проходящей через одну из них. Взаимно обратные функции. Сложная функция. Билет № 19 Сложение и вычитание векторов. Умножение вектора на число. Равносильные уравнения и неравенства. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 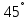 . Найдите боковое ребро параллелепипеда. . Найдите боковое ребро параллелепипеда.Билет № 20 Двугранный угол. Свойства линейных углов двугранного угла. Формулы двойного угла тригонометрических функций. Найти наименьшее и наибольшее значения функции  на отрезке на отрезке 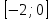 . .Билет № 21 Понятие многогранника. Призма. Площадь поверхности призмы. Формулы половинного аргумента тригонометрических функций. Билет № 22 Параллелепипед. Свойства параллелепипеда. Формулы приведения. Найдите двугранный угол ABCD тетраэдра ABCD, если углыDAB, DACиACB прямые, АС = СВ = 5 см, DB= 5 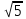 см. см.Билет № 23 Угол между прямой и плоскостью. Знаки тригонометрических функций по координатным четвертям. Решить уравнение 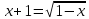 . .Билет № 24 Расстояние от точки до плоскости. Расстояние между прямыми. Тригонометрические неравенства. Решить уравнение  . .Билет № 25 Пирамида. Площадь поверхности пирамиды. Формулы зависимости между тригонометрическими функциями одного и того же аргумента. Решить неравенство 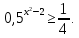 Билет № 26 Симметрия в пространстве. Платоновы тела. Формулы сложения тригонометрических функций. Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС = 13 см, ВС = 10 см, ребро АD перпендикулярно к плоскости основания и равно 9 см. найдите площадь боковой поверхности пирамиды. Билет № 27 Понятие вектора в пространстве. Коллинеарные векторы. Равенство векторов. Формулы суммы и разности тригонометрических функций. Найти все целочисленные решения уравнения 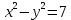 . . |
