|
|
практикум. ПРОФИЛЬ РЕШЕНИЕ. Профильный уровень егэ
Единый государственный экзамен на профильном уровне представляет собой работу, состоящую из 2 частей. Первая часть состоит из 9 заданий базового уровня, требующих краткого ответа. Данная часть работы предназначена для «проверки освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.»1
Вторая часть ЕГЭ состоит из 12 заданий повышенного уровня сложности, требующих краткого или развернутого ответа. Данная часть работы направлена на проверку освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Проведем классификацию заданий ЕГЭ профильного уровня по их порядковому номеру, оценив сложность вопроса и проанализировав его место в школьном курсе математики.
Задания №1-3
Первые 3 задания единого государственного экзамена проверяют умение учащихся использовать приобретённые знания и умения в практической деятельности и повседневной жизни. Можно провести некоторую аналогию с ОГЭ: похожие задания встречаются в заданиях итоговой аттестации 9 класса. Вычислительные навыки, умение работать с рациональными числами, анализировать, читать графики, формируемые в курсе математики 5-6 классов и алгебры 7 класса, - достаточная база, которая позволяет выполнить первые три задания ЕГЭ.
Приведем примеры заданий.
По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счёта абонента 16 руб. Если на счету осталось меньше 16 руб., то на следующее утро номер блокируют до пополнения счёта. Сегодня утром у Лизы на счету было 300 руб. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?
Решение.
300/16 = 18,75, но так как 75% от 16 рублей (т. е. 12 рублей) не хватит, чтобы оплатить день общения - делаем вывод, что Лизе этих денег хватит на 18 дней.
Ответ: 18.
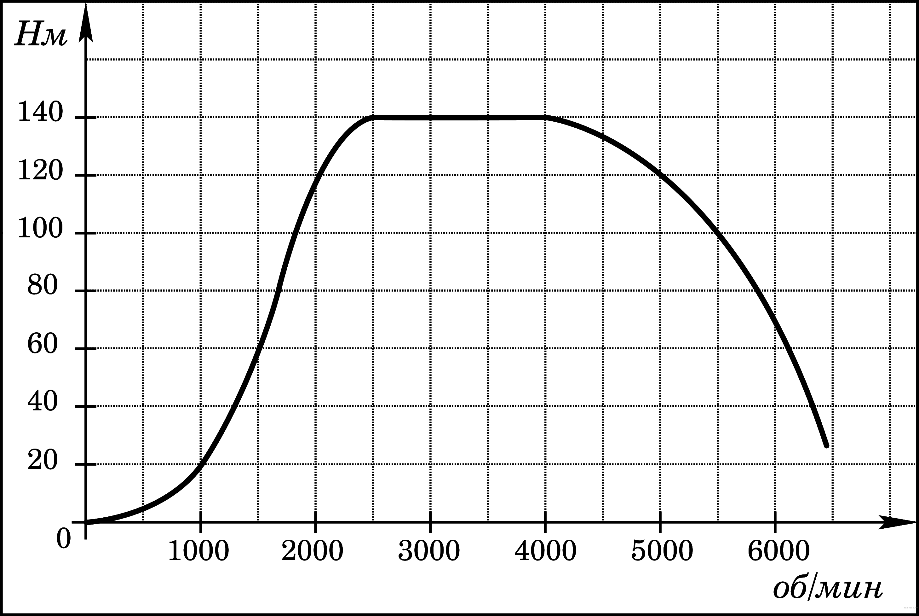
На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Нм. Скорость автомобиля (в км/ч) приближенно выражается формулой v = 0,036n, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 120 Н  м? Ответ дайте в километрах в час. м? Ответ дайте в километрах в час.
Решение.
Для того, чтобы крутящий момент был не меньше 120 Нм число оборотов двигателя в минуту n должно быть не меньше 2000 и не больше 5000 (см. график). Поэтому искомая наименьшая скорость определяется по формуле v = 0,036  2000 = 72 км/ч. 2000 = 72 км/ч.
Ответ: 72.
Семья из трех человек едет из Санкт-Петербурга в Вологду. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 660 рублей. Автомобиль расходует 8 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 19,5 рублей за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?
Решение.
Стоимость поездки на поезде для троих человек будет составлять 660  3 = 1980 руб. Расход бензина на 700 км пути составит 7 раз по 8 литров т. е. 56 литров. Его стоимость 56 3 = 1980 руб. Расход бензина на 700 км пути составит 7 раз по 8 литров т. е. 56 литров. Его стоимость 56  19,5 = 1092 руб. Стоимость самой дешевой поездки составляет 1092 рубля. 19,5 = 1092 руб. Стоимость самой дешевой поездки составляет 1092 рубля.
Ответ: 1092.
Задания №4,7
Четвертое и седьмое задания единого государственного экзамена можно объединить, так как оба этих задания проверяют умение выполнять действия с геометрическими фигурами, координатами и векторами. В них представлены планиметрические задачи, связанные с вычислением длин и площадей, нахождением углов. Математические знания, необходимые для решения данных заданий, формируются в ходе изучения геометрии 7-9 класса.
П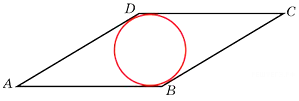 римеры заданий: римеры заданий:
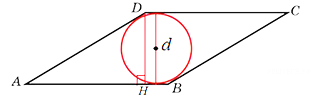 Острый угол ромба равен 30˚. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба. Острый угол ромба равен 30˚. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба.
Решение. 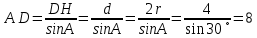
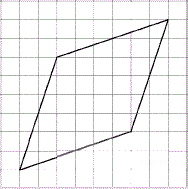 Ответ: 8. Ответ: 8.
Найдите площадь ромба, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Р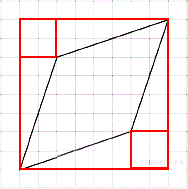 ешение. ешение.
Площадь четырёхугольника равна разности площади большого квадрата, двух маленьких квадратов и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
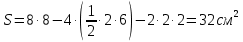
Примечание.
Наш четырёхугольник — ромб, его площадь равна половине произведения диагоналей. Диагонали ромба можно найти по теореме Пифагора, они равны 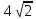 и и 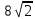 . Поэтому площадь равна 32. . Поэтому площадь равна 32.
Ответ: 32.
Задание №5
Данное задание экзаменационной работы посвящено элементам комбинаторики, теории вероятности и статистики. Для успешного выполнения данного задания от учащихся требуется знание классического определения вероятности, теорем о вероятностях событий, и умение применять их на практике. Комбинаторика как отдельный, самостоятельный раздел не изучается в курсе основной школы. Умение решать комбинаторные задачи вырабатывается при изучении математики 5-6 классов, где комбинаторика представлена фрагментарно. Понятие вероятности и задачи, посвященные ее классическому определению, разбираются в курсе 9 класса, а вот теоремам о вероятностях событий отводится время в курсе изучения алгебры 11 класса. Целесообразнее данное задание разбирать с одиннадцатиклассниками, которые уже изучили начала теории вероятности в полном объеме школьной программы. Приведем примеры заданий:
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение.
Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. События попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна 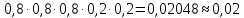 . .
Ответ: 0,02.
Задание №6
Шестое задание экзаменационной работы предполагает проверку умений учащихся решать уравнения (реже неравенства), при этом в данном задании могут встретится:
линейные, квадратные, кубические уравнения (неравенства);
рациональные уравнения (неравенства);
иррациональные уравнения (неравенства);
показательные уравнения (неравенства);
логарифмические уравнения (неравенства);
тригонометрические уравнения (неравенства).
Первые три типа уравнений и неравенств изучаются в курсе основной школы, а вот последние – в курсе старшей школы. Как показывает статистика, последние три типа уравнений, в особенности тригонометрические, являются наиболее сложными для учащихся. Поэтому учителю особенно важно обратить внимание при изучении тригонометрии на данный тип заданий.
Приведем примеры заданий.
Найдите корни уравнения: 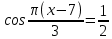 . В ответ запишите наибольший отрицательный корень. . В ответ запишите наибольший отрицательный корень.
Решение.
Последовательно получаем: 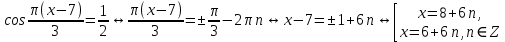 . Произведем выборку корней. Значениям . Произведем выборку корней. Значениям 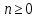 соответствуют положительные корни. Если соответствуют положительные корни. Если 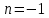 , то , то 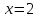 и и 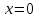 . Если . Если 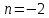 , то , то 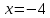 и и 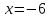 . Значениям . Значениям 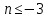 соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число -4. соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число -4.
Ответ: −4.
Найдите корень уравнения 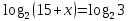 . .
Решение.
Последовательно получаем: 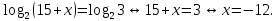
Ответ: −12.
Задание №8
В восьмом задании экзаменационной работы проверяется умение учащихся выполнять действия с функциями, в том числе используя производную и первообразную. Физический, геометрический смысл производной и касательной, применение производной к исследованию графиков, первообразная – те темы, изучение которых происходит в 10-11 классах.
Примеры заданий.
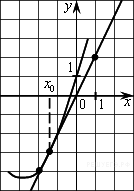
|
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс.
|
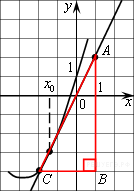
|
Построим треугольник с вершинами в точках A (1; 2), B (1; −4), С(−2; −4). Угол наклона касательной к оси абсцисс будет равен углу AСB:
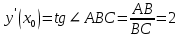
Ответ: 2.
|
На рисунке изображён график функции 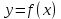 . Функция . Функция 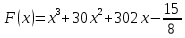 — одна из первообразных функции — одна из первообразных функции 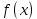 . Найдите площадь закрашенной фигуры. . Найдите площадь закрашенной фигуры.
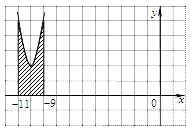
Решение.
Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках -9 и -11.
Имеем:
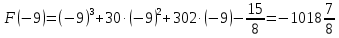 . .
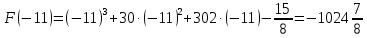 . .
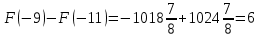 . .
Приведем другое решение. Второй подход эквивалентен выделению полного куба. Получим явное выражение для 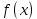 Поскольку Поскольку
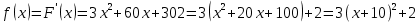
имеем: 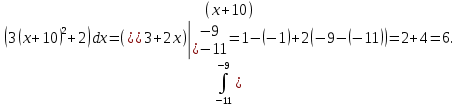
Ответ: 6.
Задание №9
Задание № 9 связано с умением решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов) и использовать при решении стереометрических задач планиметрические факты и методы. Эти умения вырабатываются в курсе изучения стереометрии 10-11 класса.
П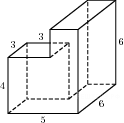 римеры заданий. римеры заданий.
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольных параллелепипедов с рёбрами 6, 6, 2 и 3, 3, 4, уменьшенной на две площади прямоугольников со сторонами 3 и 4:
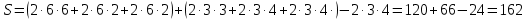 . .
Ответ: 162.
В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
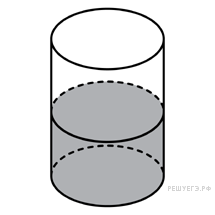 Решение. Решение.
Объём детали равен объёму вытесненной ею жидкости. Объём вытесненной жидкости равен 9/12 исходного объёма:
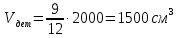 . .
Ответ: 1500.
Задание №10
Это задание проверяет умение учащихся выполнять различные вычисления и преобразования. К ним относятся преобразования числовых рациональных, алгебраических, числовых иррациональных, буквенных иррациональных, степенных выражений, а также преобразования логарифмических, показательных и тригонометрических выражений. Умения преобразовывать названные выражения вырабатывается у учащихся на протяжении всего курса изучения алгебры с 7 по 11 классы.
Приведем примеры заданий.
Найдите значение выражения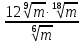 при m>0. при m>0.
Решение. Выполним преобразования: 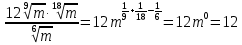
Ответ: 12.
Найдите 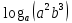 , если , если 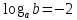 . .
Решение. Выполним преобразования: 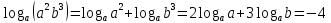 . .
Ответ: -4.
Задание №11
Данное задание направлено на проверку умений использовать приобретённые знания в практической деятельности и повседневной жизни. Задачи с прикладным содержанием, предлагаемые в данном задании, сводятся к решению линейных, квадратных, иррациональных, рациональных, степенных, логарифмических, показательных, тригонометрических уравнений и неравенств. Данные разделы алгебры изучаются также с 7 по 11 классы.
Примеры заданий.
При нормальном падении света с длиной волны 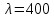 нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол φ (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума k связаны соотношением нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол φ (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума k связаны соотношением 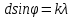 . Под каким минимальным углом . Под каким минимальным углом 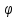 (в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1600 нм? (в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1600 нм?
Решение. Задача сводится к решению неравенства 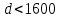 нм на интервале нм на интервале 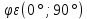 при заданных значениях длины волны света при заданных значениях длины волны света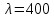 нм и номера максимума нм и номера максимума 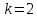 : : 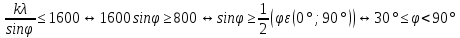 . .
Ответ: 30.
З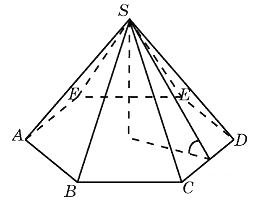 адание №12 адание №12
Задание № 12 связано с умением решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов) и использовать при решении стереометрических задач планиметрические факты и методы. Эти умения вырабатываются в курсе изучения стереометрии 10-11 класса.
Примеры заданий.
Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45 . Найдите объем пирамиды. . Найдите объем пирамиды.
Решение.
Вершина правильной пирамиды проецируется в центр ее основания. В правильном шестиугольнике со стороной  расстояние от его центра до стороны равно радиусу вписанной окружности, который равен расстояние от его центра до стороны равно радиусу вписанной окружности, который равен 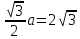 . Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна . Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна 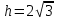 . Тогда имеем: . Тогда имеем: 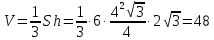 . .
Ответ: 48.
Задание № 13
Тринадцатое задание экзаменационной работы проверяет умение строить и исследовать простейшие математические модели. Встречаются задачи на проценты, сплавы и смеси, на движение по прямой, на движение по окружности, на движение по воде, на совместную работу, на прогрессии. Во-многом, задание перекликается с аналогичным № 22 в ОГЭ, поэтому можно сказать, что данное задание посильно ученику 9-го класса.
Примеры заданий.
Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение. Пусть масса первого сплава 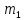 кг, а масса второго – кг, а масса второго – 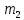 кг. Тогда массовое содержание никеля в первом и втором сплавах кг. Тогда массовое содержание никеля в первом и втором сплавах 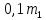 и и 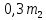 , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений: , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
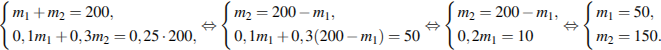
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ: 100.
Задание № 14
Умение выполнять действия с функциями проверяется в четырнадцатом задании экзаменационной работы. Оно может включать в себя исследование степенных и иррациональных функций, показательных и логарифмических функций, тригонометрических функций, исследование функций без помощи производной.
Примеры заданий.
Найдите наибольшее значение функции 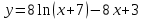 на отрезке на отрезке 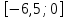 . .
Решение. Найдем производную заданной функции: 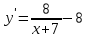 .Найдем нули производной на заданном отрезке: .Найдем нули производной на заданном отрезке:
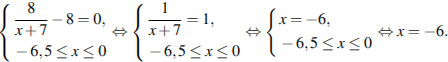
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
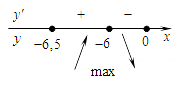
В точке 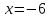 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: 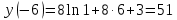 . .
Ответ: 51.
Перейдем к анализу заданий повышенного уровня сложности, составляющих вторую часть экзаменационной работы.
Задание № 15 (С1)
Пятнадцатое задание государственного экзамена проверяет умения учащихся решать различные уравнения и неравенства. В этом задании чаще всего встречаются тригонометрические уравнения, при решении которых необходимо не только найти корни, но и осуществить их выборку на заданном промежутке. Также в этом задании могут быть квадратные, рациональные, иррациональные, показательные, логарифмические и сводящиеся к ним уравнения и неравенства. Изучение данных тем происходит в 10-11 классах.
Приведем примеры таких заданий.
1. а) Решите уравнение 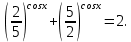
б) Найдите все корни этого уравнения, принадлежащие отрезку 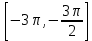 . .
Решение.
а) Введем в рассмотрение новую переменную. Пусть 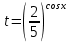 , тогда исходное уравнение запишется в виде , тогда исходное уравнение запишется в виде 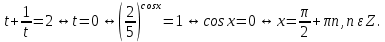
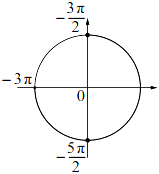 б) С помощью числовой окружности отберем корни, принадлежащие отрезку б) С помощью числовой окружности отберем корни, принадлежащие отрезку 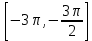
Получим числа: 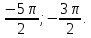
Ответ: а)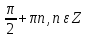 б) б) 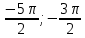
Задание №16(С2)
В данном задании экзаменационной работы учащимся предлагается стереометрическая задача, решение которой основывается на знаниях учащихся о угле между скрещивающимися прямыми, между прямой и плоскостью, между плоскостями. Ученик должен понимать, что подразумевается под расстоянием от точки до прямой и до плоскости, между прямыми и плоскостями, а также уметь находить площади сечений многогранников, объёмы многогранников и круглых тел (цилиндр, конус, шар). Данные темы изучаются в курсе стереометрии 10-11 классов.
Пример задания.
В правильной четырехугольной пирамиде MABСD с вершиной M стороны основания равны 15, а боковые ребра равны 16. Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AС.
Решение.
Пусть точка E — середина ребра MD. Отрезок BE пересекает плоскость MAС в точке P. В треугольнике MBD точка Р является точкой пересечения медиан, следовательно, MP:РО = 2 : 1, где O — центр основания пирамиды. Отрезок FG параллелен AС и проходит через точку P (точка F принадлежит ребру MA, G — ребру MС), откуда
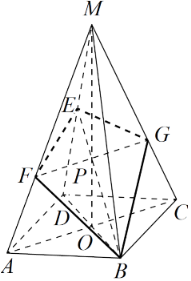 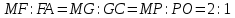
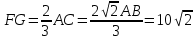
Четырёхугольник BFEG — искомое сечение. Отрезок BE — медиана треугольника MBD, значит,
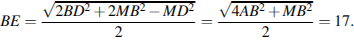
Поскольку прямая BD перпендикулярна плоскости MAС, диагонали BE и FGчетырёхугольника BFEG перпендикулярны, следовательно,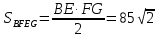 . .
Ответ: 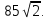
Задание №17 (С3)
Умение решать уравнения и неравенства повышенного уровня сложности проверяется в семнадцатом задании экзаменационной работы. В этом номере могут встретится как рациональные, иррациональные, показательные, логарифмические неравенства, так и их системы. Задание посильно ученику 11 класса.
Пример задания
Решите неравенство: 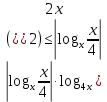 . .
Решение.
Областью определения неравенства являются положительные числа, отличные от 0,25 и 1. Выражение 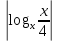 либо равно нулю при x=4, при этом неравенство верно; либо положительно, и тогда на него можно разделить, не меняя знака неравенства. Имеем: либо равно нулю при x=4, при этом неравенство верно; либо положительно, и тогда на него можно разделить, не меняя знака неравенства. Имеем:
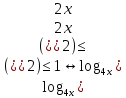
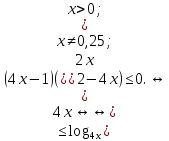
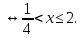
Учитывая, что 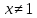 , получаем ответ , получаем ответ
Ответ: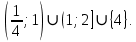
Задание №18 (С4)
Восемнадцатое задание – планиметрическая задача. Хотя 10-11 класс посвящен в основном курсу стереометрии, при изучении объемных тел так или иначе происходит повторение основных положений геометрии на плоскости. Все знания, необходимые для решения данной задачи, получаются в курсе геометрии 7-9 класса. Однако, как показывает практика проведения ЕГЭ, с данным заданием справляется менее 5% учащихся, выполняющих вторую часть экзаменационной работы.
Приведем пример задания.
Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второй раз пересекает первую окружность в точке A, а вторую — в точке D. Прямая, проходящая через точку Q параллельно AD, второй раз пересекает первую окружность в точке B, а вторую — в точке С.
а) Докажите, что четырёхугольник ABСD — параллелограмм.
б) Найдите отношение СP:PB, если радиус первой окружности втрое больше радиуса второй.
Решение.
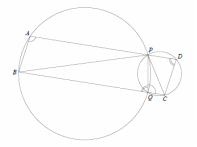 а) Обозначим а) Обозначим 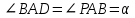 . Поскольку ABQP и CDPQ — вписанные четырёхугольники: . Поскольку ABQP и CDPQ — вписанные четырёхугольники:
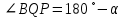
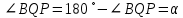
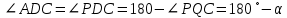
Значит, 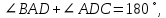 и поэтому и поэтому 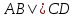 . Противоположные стороны четырёхугольника ABCD попарно параллельны, следовательно, это параллелограмм. . Противоположные стороны четырёхугольника ABCD попарно параллельны, следовательно, это параллелограмм.
б) Пусть R — радиус второй (меньшей) окружности. Тогда радиус большей окружности равен 3R. По теореме синусов:
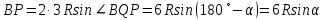 . . 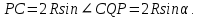 Следовательно, Следовательно, 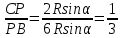 . .
Ответ: CP:PB=1:3.
Задание №19 (С5)
Пятнадцатое задание с 2015 года претерпело изменения. Теперь в нем содержится задача практического содержания, проверяющая умение учащихся использовать приобретенные знания и умения в повседневной деятельности. Согласно кодификатору элементов содержания в этом задании могут встретится задания, содержащие числа, корни, степени, логарифмы. Так как задание может содержать как проценты, изучаемые в 5 классе, так и логарифмы, изучаемые в 11 классе, сложно отнести его к какому-либо этапу изучения математики.
Пример задания
Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Решение.
Пусть сумма кредита S у.е., процентная ставка банка x %.
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Антон взятую сумму возвращал в банк равными долями. Сумма, образованная применением процентной ставки, составляет: 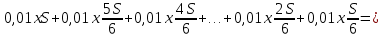
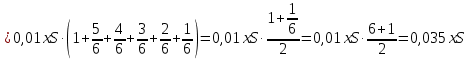 (у.е.) (у.е.)
Общая сумма, выплаченная Антоном за 6 месяцев: 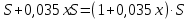 (у.е.). А эта сумма по условию задачи равна 1,63S у.е. Решим уравнение: (у.е.). А эта сумма по условию задачи равна 1,63S у.е. Решим уравнение:
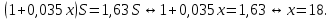
Ответ: 18.
Задание №20 (С6)
Данное задание проверяет умение учащихся решать уравнения и неравенства с параметром. Уравнения и неравенства с параметром – тема, которая мало освещена в школьном курсе изучения математики. Она является сквозной для него. Поэтому данное задание лучше предлагать выпускнику 11 класса, уже знакомому и хорошо освоившему равносильные переходы. Приведем пример задания.
При каких значениях параметра а система 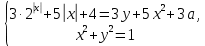 имеет единственное решение? имеет единственное решение?
Решение.
Прежде всего: заметим, что если 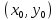 — решение системы при некотором значении параметра а, то при этом значении параметра решением системы будет и — решение системы при некотором значении параметра а, то при этом значении параметра решением системы будет и 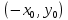 . Отсюда следует, что условие x=0 является необходимым условием существования у системы единственного решения. . Отсюда следует, что условие x=0 является необходимым условием существования у системы единственного решения.
При x=0 система перепишется в виде 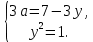
Решая эту систему относительно а, находим, что требуемые значения а могут принадлежать только множеству 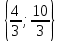 . Пусть . Пусть 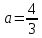 . Тогда система примет вид . Тогда система примет вид 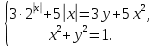
Из второго уравнения системы следует, что 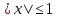 и и 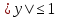 , и, таким образом, , и, таким образом, 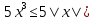 . Учитывая теперь, что . Учитывая теперь, что 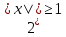 , приходим к неравенству , приходим к неравенству
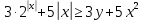 , которое означает, что первое равенство системы справедливо только при , которое означает, что первое равенство системы справедливо только при 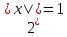 , , 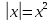 , следовательно, , следовательно, 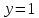 , т. е. при , т. е. при 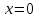 , , 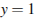 . Итак, при . Итак, при 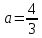 система имеет единственное решение. Пусть теперь система имеет единственное решение. Пусть теперь 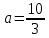 . При таком значении параметра а система перепишется в виде . При таком значении параметра а система перепишется в виде
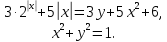
Эта система имеет решения 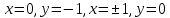 , и, таким образом, при , и, таким образом, при 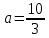 условию единственности решения не удовлетворяет. Заметим, что решения здесь просто угаданы. условию единственности решения не удовлетворяет. Заметим, что решения здесь просто угаданы.
Ответ: 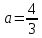 . .
Задание №21 (С7)
Последнее задание экзаменационной работы проверяет умение учащихся строить и исследовать простейшие математические модели. Задачи, предлагаемые здесь, носят логический характер и не требуют сложных математических расчетов. Они скорее с теорией чисел, которая в школьном курсе математики практически не освещена. Поэтому данное задание, на мой взгляд, нельзя отнести к какому-либо классу.
Пример задания.
За новогодним столом дети ели бутерброды и конфеты, причем каждый что-то ел, и может быть так, что кто-то ел и то и другое. Известно, что мальчиков, евших бутерброды, было не более чем 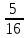 от общего числа детей, евших бутерброды, а мальчиков, евших конфеты, было не более от общего числа детей, евших бутерброды, а мальчиков, евших конфеты, было не более 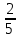 от общего числа детей, евших конфеты. от общего числа детей, евших конфеты.
а) Могло ли за столом быть 13 мальчиков, если дополнительно известно, что всего за столом было 25 детей?
б) Какое наибольшее количество мальчиков могло быть за столом, если дополнительно известно, что всего за столом было 25 детей?
в) Какую наименьшую долю могли составлять девочки от общего числа детей без дополнительного условия пунктов а и б?
Решение.
а) Если за столом было 5 мальчиков, евших только бутерброды, 8 мальчиков, евших только конфеты, и 12 девочек, каждая из которых ела и то и другое, то условие задачи выполнено. Значит, в группе из 25 детей могло быть 13 мальчиков.
б) Предположим, что мальчиков было 14 или больше. Тогда девочек было 11 или меньше. Пусть число мальчиков, евших бутерброды равно m1. Тогда число 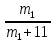 не больше , чем доля мальчиков, евших бутерброды среди всех детей, евших бутерброды, а это число не больше, чем не больше , чем доля мальчиков, евших бутерброды среди всех детей, евших бутерброды, а это число не больше, чем 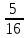 откуда откуда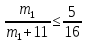 и, следовательно, и, следовательно, 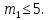 Пусть m2 — число мальчиков, евших конфеты. Аналогично, Пусть m2 — число мальчиков, евших конфеты. Аналогично,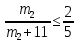 откуда, учитывая, что m2 число целое, находим: откуда, учитывая, что m2 число целое, находим: 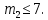 Но тогда общее число мальчиков, евших хоть что-то не больше, чем 5 + 7 = 12. Следовательно, по крайней мере, 2 мальчика ничего не ели, а это противоречит условию. Но тогда общее число мальчиков, евших хоть что-то не больше, чем 5 + 7 = 12. Следовательно, по крайней мере, 2 мальчика ничего не ели, а это противоречит условию.
В предыдущем пункте было показано, что в группе из 25 учащихся могло быть 13 мальчиков. Значит, наибольшее количество мальчиков в группе — 13.
в) Предположим, что некоторый мальчик ел и конфеты, и бутерброды. Если бы вместо него было два мальчика, один из которых ел только конфеты, а другой — только бутерброды, то доля мальчиков, евших конфеты и доля мальчиков, евших бутерброды, остались бы прежними, а общая доля девочек стала бы меньше. Значит, для оценки наименьшей доли девочек можно считать, что каждый мальчик ел или только конфеты, или только бутерброды.
Пусть, как прежде, m1 мальчиков ели бутерброды, m2 ели конфеты, и всего было d девочек. Оценим долю девочек. Будем считать, что каждая девочка ели и конфеты, и бутерброды, поскольку их доля в группе от этого не изменится, а доля среди евших конфеты и доля среди евших бутерброды не станут меньше.
По условию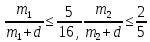 значит значит 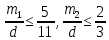
Тогда 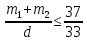 , поэтому доля девочек равна , поэтому доля девочек равна
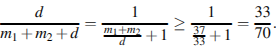
Осталось показать, что такая доля девочек действительно могла быть. Например, если из 70 детей 15 мальчиков ели только бутерброды, 22 мальчика ели только конфеты, и еще было 33 девочки, каждая из которых ела и то, и другое, то условие задачи выполнено, а доля девочек в точности равна 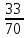 . .
Ответ:а) да; б) 13; в) 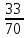
Общие выводы по профильному уровню ЕГЭ
Общие выводы по структуре ЕГЭ можно представить в таблице, где номеру задания соответствует класс, в котором данный тип изучается.
№ задания
|
Класс
|
№ задания
|
Класс
|
1
|
5-6
|
12
|
10-11
|
2
|
5-6
|
13
|
9
|
3
|
7
|
14
|
10-11
|
4
|
7-9
|
15
|
10-11
|
5
|
11
|
16
|
10-11
|
6
|
11
|
17
|
11
|
7
|
7-9
|
18
|
7-9
|
8
|
11
|
19
|
-
|
9
|
10-11
|
20
|
11
|
10
|
7-11
|
21
|
-
|
11
|
7-11
|
|
|
Как видно из таблицы, профильный уровень ЕГЭ обладает большим количеством заданий, которые могут быть решены учеником только старшей школы. Кроме двух заданий, требующих хорошо развитого логического мышления и основ теории чисел, практически половина заданий посвящена вопросам 10-11 классов, и оставшаяся половина – курсу основной школы.
|
|
|
 Скачать 299.95 Kb.
Скачать 299.95 Kb.
 римеры заданий:
римеры заданий: Острый угол ромба равен 30˚. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба.
Острый угол ромба равен 30˚. Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба.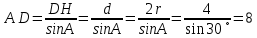
 Ответ: 8.
Ответ: 8. ешение.
ешение. 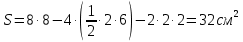
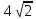 и
и 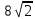 . Поэтому площадь равна 32.
. Поэтому площадь равна 32.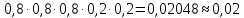 .
. 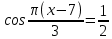 . В ответ запишите наибольший отрицательный корень.
. В ответ запишите наибольший отрицательный корень.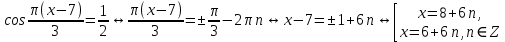 . Произведем выборку корней. Значениям
. Произведем выборку корней. Значениям 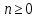 соответствуют положительные корни. Если
соответствуют положительные корни. Если 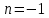 , то
, то 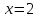 и
и 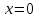 . Если
. Если 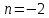 , то
, то 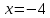 и
и 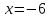 . Значениям
. Значениям 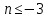 соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число -4.
соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число -4. 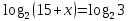 .
.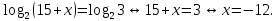
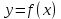 . Функция
. Функция 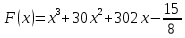 — одна из первообразных функции
— одна из первообразных функции 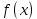 . Найдите площадь закрашенной фигуры.
. Найдите площадь закрашенной фигуры.
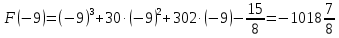 .
.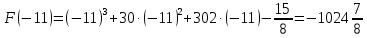 .
.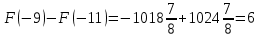 .
.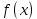 Поскольку
Поскольку 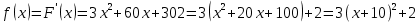
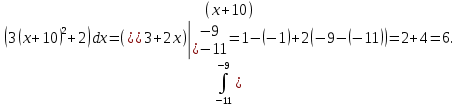
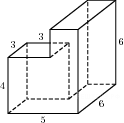 римеры заданий.
римеры заданий.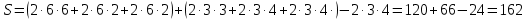 .
. Решение.
Решение.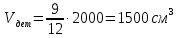 .
.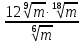 при m>0.
при m>0.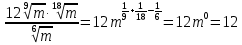
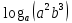 , если
, если 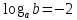 .
.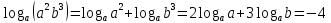 .
.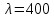 нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол φ (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума k связаны соотношением
нм на дифракционную решётку с периодом d нм наблюдают серию дифракционных максимумов. При этом угол φ (отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума k связаны соотношением 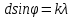 . Под каким минимальным углом
. Под каким минимальным углом 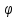 (в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1600 нм?
(в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1600 нм?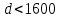 нм на интервале
нм на интервале 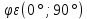 при заданных значениях длины волны света
при заданных значениях длины волны света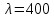 нм и номера максимума
нм и номера максимума 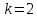 :
: 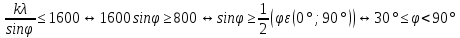 .
.


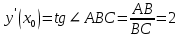
 адание №12
адание №12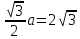 . Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна
. Так как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна 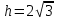 . Тогда имеем:
. Тогда имеем: 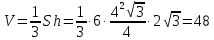 .
.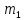 кг, а масса второго –
кг, а масса второго – 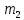 кг. Тогда массовое содержание никеля в первом и втором сплавах
кг. Тогда массовое содержание никеля в первом и втором сплавах 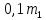 и
и 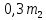 , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
, соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений: 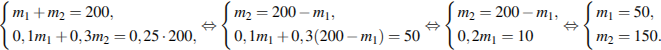
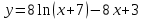 на отрезке
на отрезке 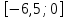 .
.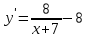 .Найдем нули производной на заданном отрезке:
.Найдем нули производной на заданном отрезке: 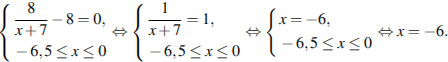
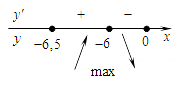
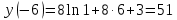 .
. 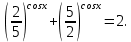
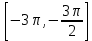 .
.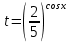 , тогда исходное уравнение запишется в виде
, тогда исходное уравнение запишется в виде 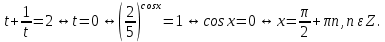
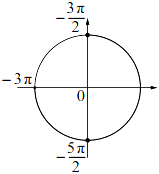
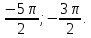
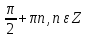 б)
б) 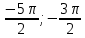

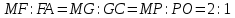
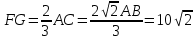
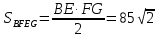 .
.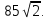
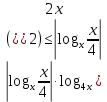 .
.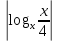 либо равно нулю при x=4, при этом неравенство верно; либо положительно, и тогда на него можно разделить, не меняя знака неравенства. Имеем:
либо равно нулю при x=4, при этом неравенство верно; либо положительно, и тогда на него можно разделить, не меняя знака неравенства. Имеем: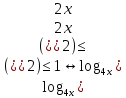
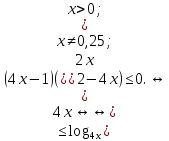
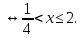
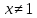 , получаем ответ
, получаем ответ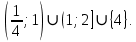

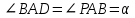 . Поскольку ABQP и CDPQ — вписанные четырёхугольники:
. Поскольку ABQP и CDPQ — вписанные четырёхугольники: 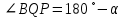
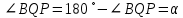
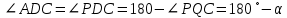
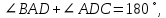 и поэтому
и поэтому 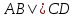 . Противоположные стороны четырёхугольника ABCD попарно параллельны, следовательно, это параллелограмм.
. Противоположные стороны четырёхугольника ABCD попарно параллельны, следовательно, это параллелограмм. 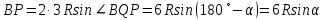 .
. 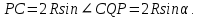 Следовательно,
Следовательно, 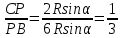 .
. 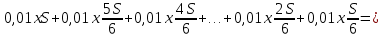
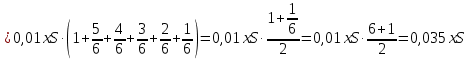 (у.е.)
(у.е.)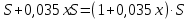 (у.е.). А эта сумма по условию задачи равна 1,63S у.е. Решим уравнение:
(у.е.). А эта сумма по условию задачи равна 1,63S у.е. Решим уравнение: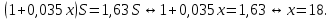
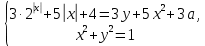 имеет единственное решение?
имеет единственное решение?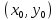 — решение системы при некотором значении параметра а, то при этом значении параметра решением системы будет и
— решение системы при некотором значении параметра а, то при этом значении параметра решением системы будет и 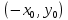 . Отсюда следует, что условие x=0 является необходимым условием существования у системы единственного решения.
. Отсюда следует, что условие x=0 является необходимым условием существования у системы единственного решения. 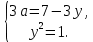
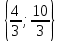 . Пусть
. Пусть 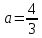 . Тогда система примет вид
. Тогда система примет вид 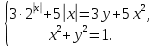
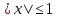 и
и 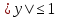 , и, таким образом,
, и, таким образом, 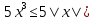 . Учитывая теперь, что
. Учитывая теперь, что 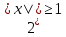 , приходим к неравенству
, приходим к неравенству 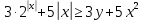 , которое означает, что первое равенство системы справедливо только при
, которое означает, что первое равенство системы справедливо только при 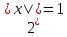 ,
, 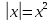 , следовательно,
, следовательно, 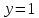 , т. е. при
, т. е. при 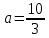 . При таком значении параметра а система перепишется в виде
. При таком значении параметра а система перепишется в виде 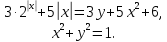
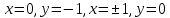 , и, таким образом, при
, и, таким образом, при 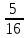 от общего числа детей, евших бутерброды, а мальчиков, евших конфеты, было не более
от общего числа детей, евших бутерброды, а мальчиков, евших конфеты, было не более 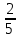 от общего числа детей, евших конфеты.
от общего числа детей, евших конфеты.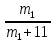 не больше , чем доля мальчиков, евших бутерброды среди всех детей, евших бутерброды, а это число не больше, чем
не больше , чем доля мальчиков, евших бутерброды среди всех детей, евших бутерброды, а это число не больше, чем 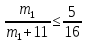 и, следовательно,
и, следовательно, 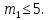 Пусть m2 — число мальчиков, евших конфеты. Аналогично,
Пусть m2 — число мальчиков, евших конфеты. Аналогично,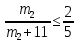 откуда, учитывая, что m2 число целое, находим:
откуда, учитывая, что m2 число целое, находим: 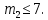 Но тогда общее число мальчиков,
Но тогда общее число мальчиков, 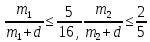 значит
значит 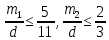
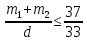 , поэтому доля девочек равна
, поэтому доля девочек равна 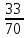 .
.