ЛР1_ФИЗИКА. Программа Для решения поставленной задачи была написана программа на языке программирования Pascal abc

• Название: Программа Для решения поставленной задачи была написана программа на языке программирования Pascal abc
• Дата: 11.03.2022
• Размер: 116 Kb.
• Имя файла: ЛР1_ФИЗИКА.doc
• Тип: Программа; #391980

Федеральное государственное бюджетное образовательное учреждение

в ысшего образования

Пермский национальный исследовательский

политехнический университет
Чайковский филиал

Кафедра автоматизации, информационных и инженерных технологий

Кафедра автоматизации, информационных и инженерных технологий
ЛАБОРАТОРНАЯ РАБОТА №1


«Создание программы для построения графиков функций»
по дисциплине «Физика»

Студент группы АСУ-19-1бз Стариков А.А,
Принял проф. кафедры АИИТ Морозов Е.А.

2020

Введение
Область исследования: Данная работа относится к компьютерному моделированию физических процессов и в частности построения графиков функций.
Актуальность: Необходимость построения графиков функций часто возникает при описании каких либо физических процессов
Цель работы: Написать универсальную программу для построения графиков функций.
Задачи:

1. 
   Написать программу
   
2. 
   Протестировать программу на примере известных функций
   
3. 
   Применить программу для исследования функций
   

1. 
   Программа
   

Для решения поставленной задачи была написана программа на языке программирования Pascal ABC.

Программа умеет строить графики фукций вида:

1. 
   y = y(t)
   
2. 
   Параметрической функции
   

x = x(t)

y = y(t)

3. 
   Полярной системы координат
   

ρ = ρ(t)

Изображение графика производится в декартовой системе координат

Предусмотрен сдвиг начала координат на экране.

Наличие сетки для более точного определения координат точки.

Имеются возможности масштабирования.

2. 
   Примеры использования программы
   

График фукции в полярной системе координат
Тема: «Тело, брошенное под углом к горизонту»
Цель: исследовать полёт тела.
Ход работы:

1. 
   Создаём программу в Pascal ABC.
   
   1. 
      Задаем углы падения снаряда в 30,45,60 градусов с помощью данного тела программы.
      

{***********График полёта тела брошенного под углом к горизонту *******}

x:=0; y:=0; tt:=0.001; t:=0; f:=45; f:=f*Pi/180; g:=9.8;

V0:=10; VX:=V0*cos(f); VY:=V0*sin(f);

for i:=1 to 100000 do

begin

VX:=VX;

VY:=VY-g*tt;

X:=x+VX*tt;

y:=y+VY*tt;

t:=t+tt;

SetPixel(x0+round(x*40*Masx),y0-round(y*40*Masy),clGreen);

end;

2. 
   Графики в 30 и 60 градусов задаются подобно.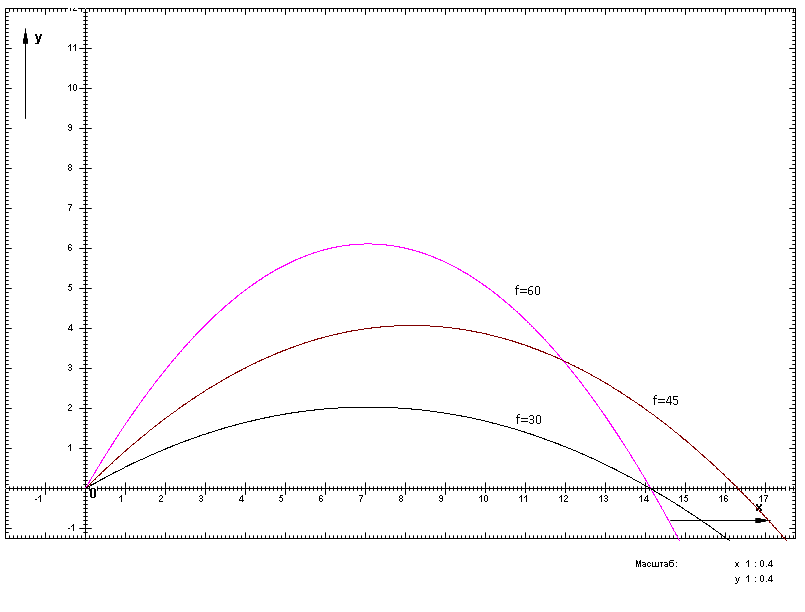
   

Рисунок 1 – Тело, брошенное под углом к горизонту


Вывод: Полет снаряда зависит от угла бросания, но незначительно.

2. 
   Исследуем полет от сопротивления воздуха.
   
   1. 
      Задаем траекторию снаряда при наличии/отсутствии сопротивления воздуха с помощью данного тела программы:
      

// траектория снаряда при наличии сопротивления воздуха

t:=0 {c} {время};

tt:=0.001 {c} {шаг интегрирования};

V0:=8{м/c} {начальная скорость снаряда};

g:=9.8 {м/сс} {ускорение свободного падения};

p0:=1.29 {кг/ммм} {плотность воздуха};

k:=0.05; {геометрический коэффициент сопротивления};

fg:=45{градусы}; f:=fg*Pi/180 {перевод градусов в радианы};

VX:=V0*cos(f); VY:=V0*sin(f){составляющие начальной скорости};

X:=0 {м}; Y:=0 {м} {начальные координаты снаряда};

m:=450 {кг} {масса снаряда};

ks:=k*pa/(2*m) {результирующий коэффициент сопротивления};

For i:=1 to 500000 do

begin

if Y<0 then Goto 5;

VX:=VX-ks*Abs(VX)*VX*tt;

VY:=VY-(g+ks*Abs(VY)*VY)*tt;

X:=X+VX*tt;

Y:=Y+VY*tt;

SetPixel(X0+round(X*40*MasX),Y0-round(Y*40*MasY), clBlack);

5:t:=t+tt;

end;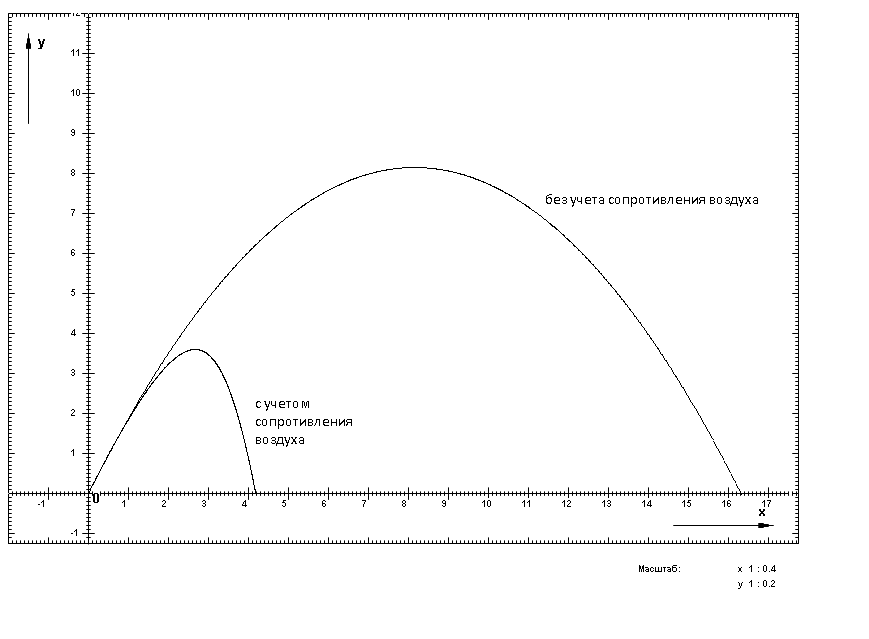



Рисунок 2 –Изменение угла полета при наличии/отсутствии сопротивления воздуха.
Вывод: Сопротивление воздуха играет значительную роль в полете снаряда, так как без сопротивления воздуха, снаряд пролетает в 3 раза большее расстояние.

3. 
   Исследуем полёт от плотности воздуха.
   
   1. 
      Задаем траекторию снаряда при учете плотности воздуха/постоянной плотности/плотности уменьшающейся по экспоненте при помощи данного тела программы:
      

t:=0 {c} {время};

tt:=0.001 {c} {шаг интегрирования};

V0:=8{м/c} {начальная скорость снаряда};

g:=9.8 {м/сс} {ускорение свободного падения};

mm:=0.029 {молярная масса воздуха};

R0:=8.31 {универсальная газовая постоянная};

TK:=273 {К} {температура воздуха};

H0:=(mm*g)/(R0*TK) {константа высоты};

pa:=EXP(1.29) {кг/мм} {плотность воздуха};

k:=0.05; {геометрический коэффициент сопротивления};

fg:=45{градусы}; f:=fg*Pi/180 {перевод градусов в радианы};

VX:=V0*cos(f); VY:=V0*sin(f) {составляющие начальной скорости};

X:=0 {м}; Y:=0 {м} {начальные координаты снаряда};

m:=450 {кг} {масса снаряда};

ks:=k*pa/(2*m);

For i:=1 to 500000 do

begin

if Y<0 then Goto 8;

VX:=VX-ks*Exp(-H0*X)*Abs(VX)*VX*tt;

VY:=VY-(g+ks*Exp(-H0*Y)*Abs(VY)*VY)*tt;

X:=X+VX*tt;

Y:=Y+VY*tt;

SetPixel(X0+round(X*40*MasX),Y0-round(Y*40*MasY), clBlack);

8:t:=t+tt;

end;



Рисунок 3 - Изменение угла полета при учете плотности воздуха/постоянной плотности/плотности уменьшающейся по экспоненте.
Вывод: Плотность имеет значительное влияние на траекторию снаряда.

Общий вывод: Исследовав траекторию 3-мя различными способами, (угол, сопротивление воздуха, плотность воздуха) я могу сказать, что все эти факторы имеют какое-либо влияние на траекторию. Цель лабораторной работы выполнена.