Программа магистратуры Международная экономика

• Название: Программа магистратуры Международная экономика
• Дата: 12.03.2019
• Размер: 0.6 Mb.
• Имя файла: Dom_zadania_MIKRO_ZO_17-18.docx
• Тип: Программа; #70240

ВСЕРОССИЙСКАЯ АКАДЕМИЯ ВНЕШНЕЙ ТОРГОВЛИ

МИНЭКОНОМРАЗВИТИЯ РОССИИ

Факультет международного бизнеса
Программа магистратуры «Международная экономика»

заочная форма обучения


ДОМАШНЕЕ ЗАДАНИЕ

по дисциплине

«Микроэкономика»

Часть II – задачи и задания с открытым ответом

Проверил преподаватель: __________ /___________/ « ___ » _________ 201__г.

Выполнил студент: ___ курса (набор _____ года) __________ /___________/ «___» ____________ 201__г.

Москва

201__г.

1. 
   На мировом рынке резко упали цены на нефть. Объясните, как это может повлиять на состояние валютного рынка в России.
   

Графическая иллюстрация.
Решение:

При падении мировой цены на нефть стоимость российского экспорта резко сократится при неизменном импорте. Это вызовет удорожание доллара.

Для восстановления курса рубля ЦБ может увеличить предложение валюты за счет собственных резервов. в результате чего кривая совокупного предложения сместится вправо (S—>S1) При неизменном спросе (D) кол-во (Q—>Qi) увеличится, а цена доллара упадет (P^Pi) Продавая валюту и изымая часть рублевой массы в обмен. ЦБ тем самым уменьшит денежную массу.

Графическая иллюстрация.
S₁

D

P

P₁

Q

Q₁

Q

P


2. Даны функции спроса и предложения: P=80-5q, P=32+q.

Рассчитайте равновесную цену и равновесное количество данного товара.

Если государство запретит продавать товар дороже, чем по 35 руб., то каким будет дефицит?

Решение

Условие равновесия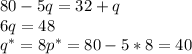 



Hавновесная цена превышает допустимую, поэтому нам нужно найти объем спроса и объем предложения при цене 35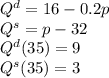



Количество предложения при цене 35 равно 3, а количество спроса 9, тогда дефицит(x) равен:



График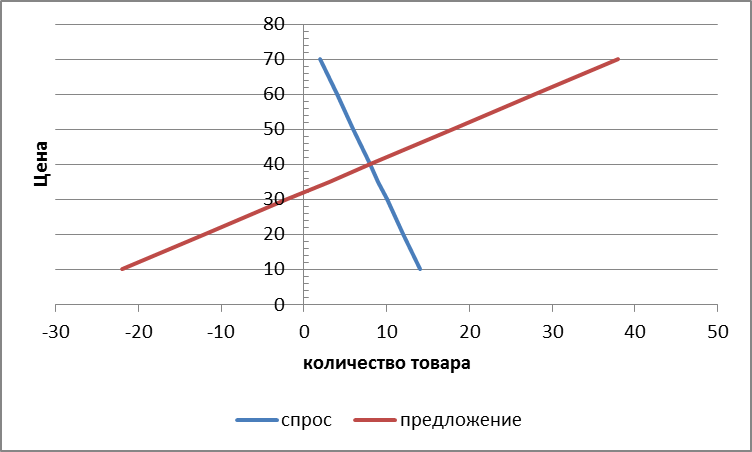

дефицит
Ответ: 6

3. Первоначальная цена товара составляла 20 руб. При этом его ежедневный сбыт был 500 шт. После повышения цены до 30 руб. спрос на товар упал до 400 шт.

А. Рассчитайте эластичность спроса по цене (в каждой из точек и дуговую)

Б. Сделайте выводы о целесообразности повышения цены с точки зрения увеличения выручки производителей данного товара.

Решение

А. Точечная эластичность применяется при малых приращениях (обычно до 5%) или в абстрактных задачах, где задаются непрерывные функции спроса: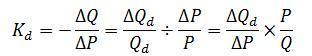



Эластичность спроса в точке 1: Кd=-100/-10*20/500=-0.4,

Эластичность спроса в точке 1: Кd=-100/10*30/400=-0.75,

Дуговая эластичность - В случаях когда изменение цены и/или спроса значительные (более 5 %) принято рассчитывать дуговую эластичность спроса:  где и  — средние значения соответствующих величин. То есть, при изменении цены от до и объёма спроса с до , среднее значение цены будет составлять ,а среднее значение спроса 

Е^D_p=-100/(0.5*(500+400)/(10/0.5*(20+30))=-0.33 – спрос неэластичен, так как коэффициент эластичности меньше 1.

При повышении цены процент снижения спроса меньше, чем изменение цены. При повышении цен в разумных пределах производителю выгодно повышать цену так от 500 единиц производитель получал 10000 выручки, а при повышении цены до 30 он получит при реализации 400 ед. 12000 руб., что выгодно с позиций производителя.
Б. Цену повышать не стоит, спрос упадёт.
4. Дана функция спроса по доходу: q=5+1,5I (I- размер дохода). Определите эластичность спроса по доходу при его размере 100 у.е.

Решение

Объем спроса равен q=5+1,5*100=155, тогда эластичность спроса Е^dд=dQ/dI*I/Q

dQ/dI=5. Тогда эластичность равна Е^dд=5*100/155=3,323 В данном случае речь идет о предметах роскоши

5.Функция спроса на товар X имеет вид: Qd,= 8 – Р_x+ 0,4 Ру

где Рх, Ру — рыночные цены товаров X и Y.

Определите коэффициенты прямой и перекрестной эластичности спроса на товар X при Рх=4 долл. и Ру = 5 долл.

Решение

Коэффициент прямой эластичности

Ex = (∂Q/∂Px)•Px/Q = -1•Px/(8-Px+0.4Py) = -1•4/(8-4+0.4•5) = -4/6 = -1/3 ≈ -0.667
Коэффициент перекресной эластичности

Ey = (∂Q/∂Py)•Py/Q = 0.4•Py/(8-Px+0.4Py) = 0.4•5/(8-4+0.4•5) = 2/6 ≈ +0.333
6. В конце года бухгалтер говорит Вам, что Ваша прибыль составляет 400000 руб. Управляя своей собственной фирмой, Вы упускаете зарплату в 250000 руб., которую вы могли бы получить, работая в другом месте. У Вас также 1000000 руб. собственных средств вложены в Ваш бизнес.

Предполагая, что Вы упускаете 12% годового дохода с этих вложенных средств, подсчитайте экономическую прибыль.

Останетесь ли Вы в этом бизнесе на следующий год? Обоснуйте свое утверждение. (Предполагается, что свои средства Вы можете легко и без потерь вывести из бизнеса.)

Решение

Экономическая прибыль равна бухгалтерской прибыли за минусом упущенных возможностей. Таким образом, экономическая прибыль составит 
400 000 - (250 000 + 1 200 000*12%) = 400 000 - (250 000 + 120 000) = 
400 000 - 370 000 = 30 000

Т.е. бизнес прибыльный, но при небольших изменениях на рынках (труда, %, продукции) баланс может измениться. На следующий год можно остаться в этом бизнесе.

7. Заполните пустые клетки:

Q	FC	VC	TC	AFC	AVC	AC	МС
100	2000	1000	3000	20	10	30	10
200	2000	2000	4000	10	10	20	10

Решение

Q – количество, TC – общие затраты, VC – переменные затраты, FC – фиксированные затраты, AC – средние затраты, AVC - средние переменные затраты, AFC – средние фиксированные затраты, MC – предельные затраты.

При Q = 100, AFC = 20, AFC = FC / Q, следовательно, FC = 20*100 = 2000 при любом объёме выпуска. Заполняем столбец FC полностью. AVC(1) = VC / Q

VC(1)= AVC* Q=10*100=1000, VC(2)= AVC* Q=10*200=2000

TC (1)= VC + FC = 2000+1000=3000 TC (2)= VC + FC = 2000+2000=4000

AFC(2) = FC / Q=2000/200=10

АС(1) = TC / Q = 3000/100=30

MC(1) = (TC(1) – TC(0)) / (100 – 0) = (3000-2000)/100= 10

MC(1) = (TC(1) – TC(0)) / (100 – 0) = (4000-3000)/100= 10

8. АНАЛИЗ ПРАКТИЧЕСКОЙ СИТУАЦИИ

Рыболовное судно может войти в порт и покинуть его только во время прилива с 6 до 7 часов. На практике судно располагает 24 часами на путь до места лова и обратно и собственно ловли рыбы. Зона лова находится в 30 милях от порта. Чем быстрее судно туда доберется, тем больше времени оно сможет потратить на саму ловлю. В тоже время расход топлива зависит от скорости:

Скорость (миль/час)	Расход топлива (галлонов на 60 миль)
6	10
7	11
8	13
9	16
10	20
11	25
12	31
13	38

Во время ловли топливо не расходуется. Цена топлива равна $1 за галлон. Все прочие расходы от скорости не зависят. Каждый час лова позволяет добыть рыбу, стоимостью $10.

Какую скорость должно выбрать судно, если его владелец хочет максимизировать прибыль?

Решение

а) Способ 1. Сопоставление валового дохода и валовых издержек:

Определим величину валового дохода по формуле:

TR = Q × P,

где

TR – валовой (общий) доход от продажи рыбы,

Q – выпуск или количество произведённого товара  (в данном кейсе количество часов лова),

Представим время лова функцией, зависящей от скорости (υ) судна: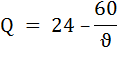



Р – цена товара (в данном кейсе стоимость рыбы, пойманной за час, то есть $10).

Тогда функция выручки будет иметь вид: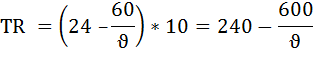



Валовые (общие) издержки TC, состоят только из расходов на топливо.

ТС = Расход топлива × Р_{топлива},

где

Р_{топлива} – цена топлива.

Так, например, при скорости судна 6 миль/ч общий доход будет равен: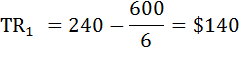



а величина валовых затрат:

TC1 = 10 × 1 = $10

Аналогично производится расчёт валового дохода и валовых издержек при остальных значениях скорости.

Результаты вычислений занесём в таблицу.

Скорость (миль/час)	Расход топлива (галлонов на 60 миль)	TC,$	TR,$	TR – TC, $
6	10	10	140,00	130,00
7	11	11	154,29	143,29
8	13	13	165,00	152,00
9	16	16	173,33	157,33
10	20	20	180,00	160,00
11	25	25	185,45	160,45
12	31	31	190,00	159,00
13	38	38	193,85	155,85

Сопоставив валовой доход и валовые издержки, приходим к выводу, что прибыль

П = TR – TC

будет максимальной при скорости судна 11 миль/ч.
 б) Способ 2. Сопоставление предельного дохода и предельных издержек.

 Предприятие (в данном случае владелец судна), которое стремится к максимуму  прибыли, выберет такой объём производства, при котором предельные затраты будут равны предельному доходу.

То есть когда выполняется равенство:

MС = MR.

Предельные затраты (МС) – это прирост общих затрат, связанный с ростом выпуска продукции на дополнительную единицу.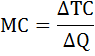



Предельная выручка (MR) – это прирост выручки, связанный с ростом выпуска продукции на дополнительную единицу.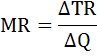



Предельная прибыль (Мπ) – это прирост общей прибыли, связанный с производством дополнительной единицы продукции. Предельную прибыль можно  найти также как разность предельной выручки и предельных затрат: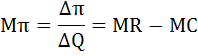



Правило принятия решения об объёме производства  гласит: пока предельная прибыль положительна, предприятию следует наращивать объём производства. В данном кейсе переформулируем: пока предельная прибыль положительна, судну следует наращивать время ловли, а следовательно, увеличивать скорость движения к месту ловли.

Рассчитаем величину времени лова, предельных затрат, предельной выручки и предельной прибыли.

При скорости υ = 6 миль/час время лова будет равно: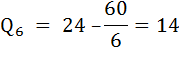



При скорости υ = 7 миль/час время лова будет равно: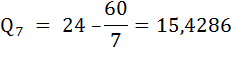



Предельные издержки: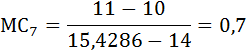



Предельная выручка: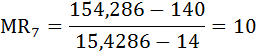



Предельная прибыль:

Мπ₇ = MR₇ – MC₇ = 10 – 0,7 = 9,3

Результаты остальных вычислений занесём в таблицу.

Скорость (миль/час)	Q	TC,$	TR,$	MC, $	MR, $	Мπ = MR – MC, $
6	14	10	140,00	-	-	-
7	15,4286	11	154,29	0,7	10	9.3
8	16,5	13	165,00	1,8667	10	8,1333
9	17,3333	16	173,33	3,6	10	6,4
10	18	20	180,00	6	10	4
11	18,5455	25	185,45	9,1667	10	0,8333
12	19	31	190,00	13,2	10	-3,2
13	19,3846	38	193,85	18,2	10	-8,2

Из таблицы видно, что предельная прибыль положительна при Q =18,55 и при скорости движения υ = 11 миль/час, а вот уже при Q = 19 торопиться не стоит, так как предельная прибыль уже приняла отрицательное значение. Следовательно, скорость, которую должно выбрать судно, если его владелец хочет максимизировать прибыль должна быть 11 миль/час.

9. Приведенный ниже график иллюстрирует принцип выбора цены и объема производства, при котором фирма - монополист получает максимальную прибыль

а) Надпишите аббревиатуры к каждой из линий, обозначенных на нижеприведенном графике.

б) Покажите цену и объем производства, которые выберет фирма.

в) Добавьте в график недостающий элемент и определите (заштриховав необходимую площадь) размер прибыли (или убытков), получаемой фирмой.

РЕШЕНИЕ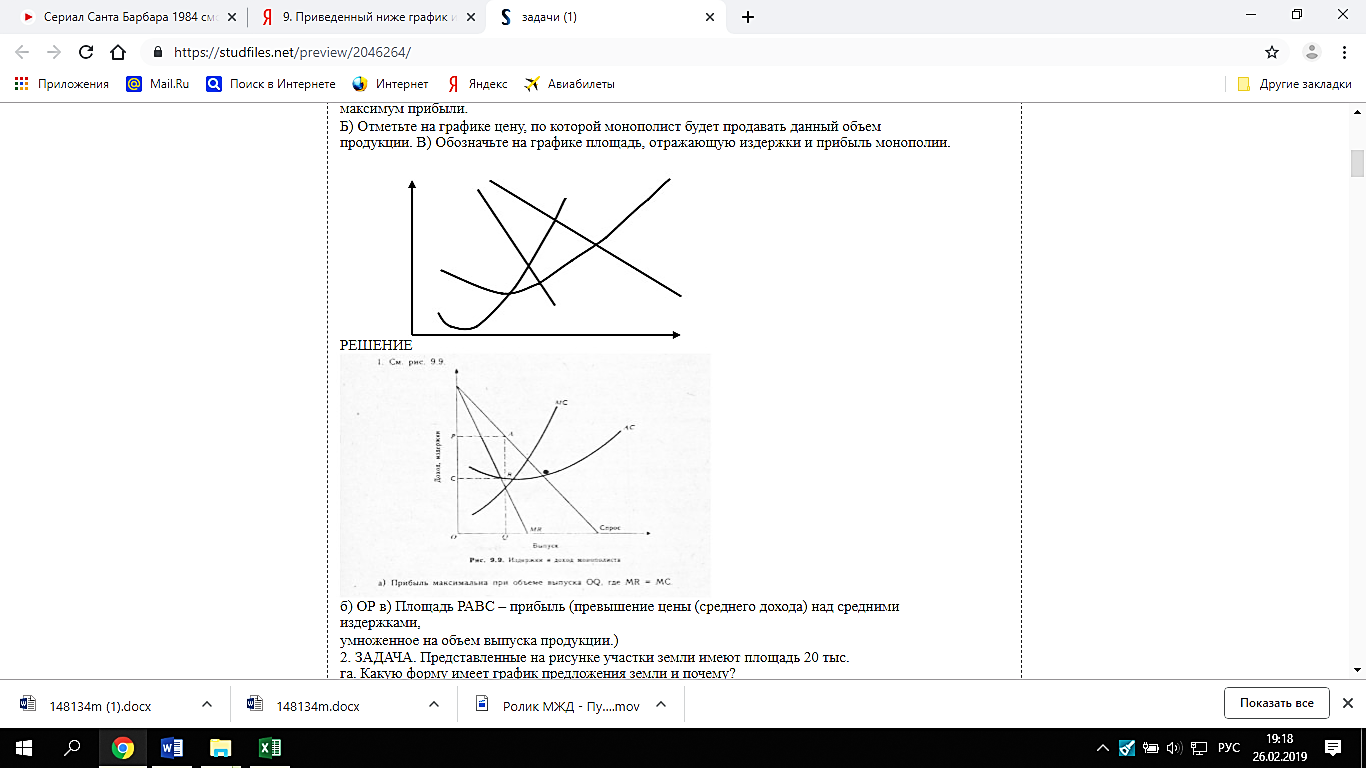



б) ОР в) Площадь РАВС – прибыль (превышение цены (среднего дохода) над средними издержками,

умноженное на объем выпуска продукции.)
10.Спрос на продукцию монополии задан функцией P= 40-2q. Функция суммарных затрат монополии: TC = 100 + 4q. Определить монопольную цену,, объем продаж и прибыль..

РЕШЕНИЕ

Условие максимизации прибыли монополии MC = MR.

MC = TC’(Q) = 4;

MR = TR’(Q) = (P∙Q)' = ((40– 2Q)Q)’ = (40Q – 2Q²)’ = 40–4 Q. Тогда: 4 = 40–4Q, следовательно максимизирующий прибыль монополии объем продаж Q = 9 ед.; P = 40– 2*9 = 22 ден. ед.

Условие максимизации выручки монополии: MR = 0. Тогда: 40 – 4Q = 0; Q = 10 ед. P = 20 ден.ед.

π_max = TR – TC = 40-4*9 –100 + 4*9 = -132 ден.ед.

Несовпадение объема выпуска при максимизации прибыли и выручки легко объяснить геометрически: максимизация предполагает равенство тангенсов углов наклона касательных к соответствующим функциям. При максимизации прибыли – это касательные к функциям выручки и затрат, а при максимизации выручки – угол наклона касательной к функции выручки равен нулю.
11. Компания "Джеральде" — монополист на рынке. Функция полных затрат на производство: ТС = 2Q + 10, где Q — объем производства в месяц. Определите, при каком уровне цены прибыль компании будет максимальной, если известно, что эластичность рыночного спроса в этой точке по цене равна -6. (при решении использовать коэффициент лернера)

РЕШЕНИЕ

Обратите внимание на характер функций предельных и средних издержек. MC = 2; АС = 2 + 10/Q. Это случай естественной монополии. Конкурентный характер рынка здесь невозможен, так как фирма при Р = MC всегда терпит убытки.

L  = -1/Е  = - 1 / - 6, где Е – эластичность.

Монопольная власть оценивается по индексу Лернера: L = (Р - МС)/Р:

L  = (Р - 2)/Р = 1/6, т. е. Р = 2,4.
12. Есть данные о деятельности совершенно-конкурентной фирмы:

Выручка (TR)=10000

Выпуск (q)=1000

Постоянные затраты (FC)=4000

Переменные затраты (VC)=8000

Предельные затраты (MC)=10

РЕШЕНИЕ
При ответах на нижеследующие вопросы дайте их краткие обоснования

1. 
   Находится ли фирма в состоянии краткосрочного равновесия?
   

Ответ: Условием равновесия фирмы, как в краткосрочном, так и в долгосрочном периоде является равенство предельных издержек и предельного дохода MC=MR.

МR=TR/q=10000/1000=10. Таким образом фирма находится в условии равновесия

2. 
   Должна ли фирма продолжать свою деятельность в коротком периоде?
   

Ответ: Прибыль фирмы равна TR-(FC+VC)=10000-(4000+8000)=-2000. Фирма получает убыток, следовательно в коротком периоде фирме не выгодно продолжать свою деятельность.

3. 
   Останется ли фирма на рынке в долгосрочном периоде при данных экономических показателях?
   

При данных экономических показателях фирма уйдет с рынка, так как цен меньше средней издержек цена 10, а средние переменные издержки – 12.

4. 
   Проиллюстрируйте ситуацию графически:
   

1. Условием равновесия фирмы, как в краткосрочном, так и в долгосрочном периоде является равенство предельных издержек и предельного дохода MC=MR. 

МR=TR/q=10000/1000=10. Таким образом фирма находится в условии равновесия

2.Прибыль фирмы равна TR-(FC+VC)=10000-(4000+8000)=-2000. Фирма получает убыток, следовательно в коротком периоде фирме не выгодно продолжать свою деятельность.

3.При данных экономических показателях фирма уйдет с рынка, так как цен меньше средней издержек цена 10, а средние переменные издержки – 12.
4.Проиллюстрируйте ситуацию графически:

Равновесие фирмы в краткосрочном периоде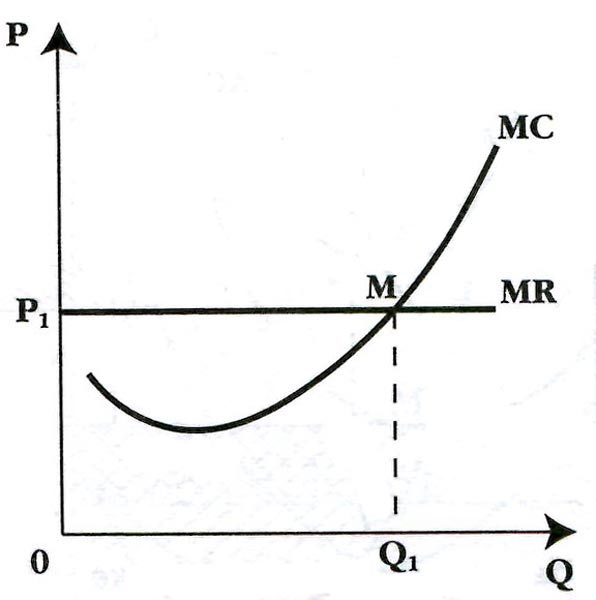



Равновесие фирмы в долгосрочном периоде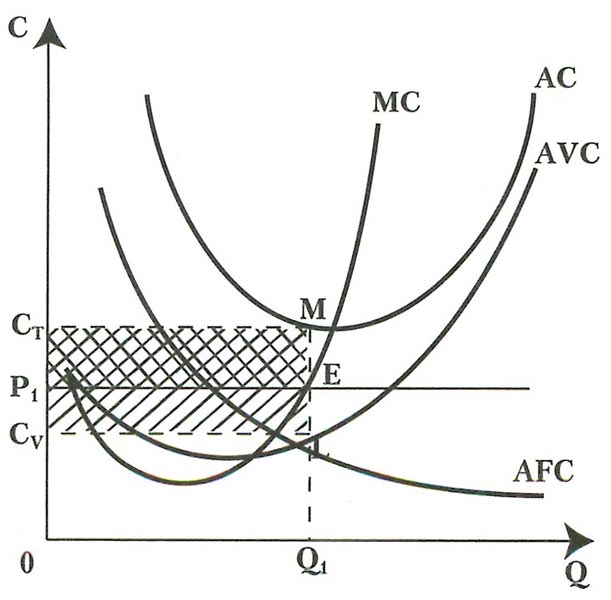



Р1=12 а у нас имеется 10, что ниже точки М.

13. Функция рыночного спроса на продукт отрасли

P = 9,6 – Q, где Q – общий выпуск всех фирм отрасли. В отрасли действуют две фирмы. Функция совокупных затрат первой: TC₁=q₁², а второй: TC₂=1,5q₂². Фирмы образовали картель.

Ответьте на вопросы:

1) какой будет квота каждой фирмы?

2) сколько прибыли получит каждая фирма при соблюдении квоты?

Проиллюстрируйте решение графически. Объясните, почему у каждой фирмы возникает соблазн нарушить соглашение.

РЕШЕНИЕ

На рынке действуют две фирмы. Функция издержек для фирмы 1:

Подставим общий выпуск двух фирм Q = q₁ + q₂

в формулу отраслевого спроса, получим:

P(Q) = 9.6 – 1 × (q₁ + q₂)

Распишем прибыли олигополистов:

П₁ = TR₁ – TC₁ = P × q₁ – 2 × q₁ = (9.6 – 1 × (q₁ + q₂)) × q₁ – q₁²=

= 9.6q₁ –q₁²–q₁ q₂ –q₁ ²=9.6 × q₁ – 2q₁² – q₁q₂

П₂ = TR₂ – TC₂ = P × q₂ – q₂² = (9.6– (q₁ + q₂)) q₂ – 1.5q₂² =

 = 9.6q₂ –q₂² – q₁ q₂ – 1.5q₂² =9.6q₂ – 2.5q₂² – q₁q₂

Каждая фирма стремится к максимуму прибыли.

Найдём максимум функций прибыли. Для этого приравняем к нулю первые производные полученных функций и найдём оптимальный объём выпуска:

П₁' = (9.6 × q₁ – 2q₁² – q₁q₂)’ =9.6-4q₁- q₂

П₂' = (9.6q₂ – 2.5q₂² – q₁q₂)= 9.6-5q₂-q₁

Уравнение реакции для 1 фирмы: q₁ = 9.6– 5× q₂ 

Уравнение реакции для 2 фирмы: q₂ = 9.6– 4 × q₁

Точка пересечения этих линий определяет рыночное равновесие для монополистов.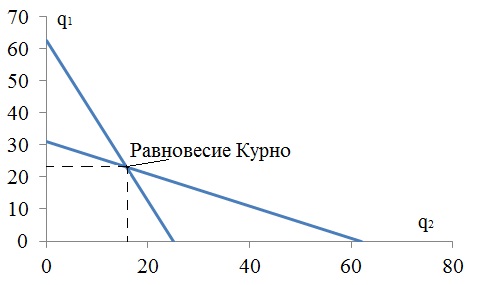



Решив систему из двух уравнений реакции дуополистов, получим равновесные значения выпуска для первой и второй фирмы.

q*₁ = 2.02

q*₂ = 1.52

Подставив равновесные значения q*₁ и q*₂ в функцию отраслевого спроса

P(Q) = 9.6 –(q₁ + q₂),

найдём цену равновесия.

Р =9.6– (2.02+1.52)= 6.06

Рассчитаем прибыль каждой фирмы в отдельности:

П₁ = 2.02*6.06-2.02²=8.52

П₂ = 1.52*6.06-1.5*1.52² = 5.75

У каждой фирмы выступает соблазн нарушить соглашение, так как все фирмы стремяться максимизировать свою прибыль.