ЛР 2 маятниковый маршрут. Программа оптимизации маятниковых маршрутов с обратным холостым пробегом

Название	Программа оптимизации маятниковых маршрутов с обратным холостым пробегом
Анкор	ЛР 2 маятниковый маршрут
Дата	18.11.2021
Размер	203.5 Kb.
Формат файла
Имя файла	ЛР 2 маятниковый маршрут.doc
Тип	Программа #275660
страница	1 из 2

1 2

^{Автор – Дроздов Петр}
^{Компьютерная программа оптимизации маятниковых маршрутов}

^{с обратным холостым пробегом}
^{Транспорт, являясь базовой отраслью национальной экономики государства, обеспечивает взаимосвязь его элементов и способствует углублению территориального разделения труда.}

^{Значительный объем грузов (до 85%) в народном хозяйстве перевозится автомобильным транспортом, который является неотъемлемой составной частью транспортной системы национальной экономики, ее наиболее гибким и мобильным компонентом. В этой связи весьма актуальным является}^{рациональное управление автотранспортом, которое включает оптимизацию}^{маятниковых}^и^{кольцевых}^{маршрутов и позволяет при одних и тех же объемах грузоперевозок снизить транспортную работу, а также потребление горюче-смазочных материалов до 15–20 %.}

^{Маятниковый маршрут}^{– такой маршрут, при котором путь следования транспортного средства (автомобиля, тракторно-транспортного агрегата) между двумя (и более) грузопунктами неоднократно повторяется.}

^{Маятниковые маршруты бывают:}

^{– с обратным холостым пробегом;}

^{– с обратным неполностью груженым пробегом;}

^{– с обратным груженым пробегом.}

^{Как показывает практика,}^{самым распространенным и}^{при этом}^{самым неэффективным}^{видом маятниковых маршрутов в практике хозяйственной деятельности является маршрут с обратным холостым пробегом (рисунок 1).}

Б – товарная база (место загрузки транспорта); П – потребитель товара;

l_ег– груженая ездка; l_х – холостой (порожний) пробег.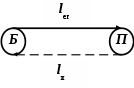

^{Рисунок 1. – Графическое представление маятникового маршрута}

^{с обратным холостым пробегом}

^{Примером маятникового маршрута с обратным холостым пробегом является следующая производственная ситуация: на конкретную дату потребителю необходимо доставить 100 тонн груза с помощью одного самосвала грузоподъемностью 10 тонн, то есть самосвал сделает 10 груженых ездок потребителю.}

^{Повышение эффективности использования автотранспорта на маятниковых маршрутах с обратным холостым пробегом возможно (при прочих равных условиях) путем увеличения технической скорости транспорта, применения прицепов, максимального использования грузоподъемности транспорта, сокращения времени на погрузочно-разгрузочные работы, а также в результате оптимальной маршрутизации.}
^{Прежде чем рассмотреть оптимизацию маятниковых маршрутов с обратным холостым пробегом,}^{представим определения необходимых базовых понятий:}

^1.^Груз^{– это товар или материальный ресурс принятый к перевозке. При этом, если груз упакован в определенную тару и защищен от внешних механических и атмосферных воздействий, то такой груз называется транспортабельным.}

^2.^Ездка^{– законченная транспортная работа, включающая погрузку товара, движение автомобиля с грузом, выгрузку товара и подачу транспортного средства под следующую погрузку.}

^3.^{Груженая ездка}^{– это путь движения автомобиля с грузом.}

^4.^{Порожний (холостой) пробег}^{– это путь движение автомобиля без груза.}

^5.^Оборот^{– выполнение автомобилем одной или нескольких транспортных работ (ездок) с обязательным возвращением его в исходную точку.}

^6.^{Время на маршруте}^{– это период времени с момента подачи автомобиля под первую погрузку до момента окончания последней выгрузки.}

^7.^{Время в наряде}^{– это период времени с момента выезда автомобиля из автопарка до момента его возвращения в автопарк.}

^8.^{Первый нулевой пробег}^{– путь движения автомобиля из автопарка к месту первой погрузки.}

^9.^{Второй нулевой пробег}^{– путь движения автомобиля из места последней разгрузки в автопарк.}

^10.^{Техническая скорость,}^{которая представляет собой отношение общего пробега (}^l_общ^{) автомобиля за рабочий день к времени}^{движения (}^t_дв^{), которое включает кратковременные остановки, регламентированные правилами дорожного движения.}
^{Следует подчеркнуть, что в случае если оптовая база имеет собственный подвижной состав автомобильного транспорта, то в данной ситуации время в наряде равно времени на маршруте.}

^{Реализацию задачи оптимизации маятниковых маршрутов с обратным холостым пробегом}^{рассмотрим на примере следующей производственной ситуации. В соответствии с заключенными договорами на оказание транспортных услуг автотранспортное предприятие (АТП) 24 июня 2009 г. должно обеспечить доставку гравия трем потребителям П}₁^{, П}₂^{и П}₃^{, потребности которых составляют соответственно 30, 40 и 50 м}³^{. При этом оговорено, что доставка должна быть обеспечена независимо от времени рабочего дня. Расстояния в километрах пути между АТП и потребителями, а также между потребителями и карьером (К) откуда будет осуществляться доставка гравия, представлены на схеме (рисунке 2).}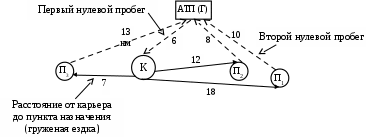

Рисунок 2. – Схема размещения автотранспортного предприятия (АТП), карьера (К) и потребителей (П)
^{Следует отметить, что при составлении данной схемы наряду с обеспечением минимального расстояния между соответствующими пунктами, необходимо учитывать следующие факторы: фактическое состояние дорожного покрытия, количество возможных кратковременных остановок регламентированных правилами дорожного движения и т.п. Это позволит с одной стороны сократить физический износ техники в результате ее производственной эксплуатации, а с другой – увеличить производительность автотранспорта. Так, в нашем примере (см. рисунок 2) длина груженой ездки от точки К до П}₁^{составляет 18 км, что больше суммы первого и второго нулевого пробегов (6 + 10 = 16 км) и обусловлено учетом вышеуказанных факторов.}

^{Транспортировка груза в соответствии с договорами будет осуществляться автомобилями МАЗ с емкостью грузовой платформы 5}^м³^{. В этой связи в пункт П}₁^{потребуется сделать 6 ездок (30 м}³^{: 5 м}³^{), в пункты П}₂^{и П}₃^{– 8 и 10 ездок соответственно. Наряду с этим принималось, что время работы автомобилей в наряде – 8 часов, тех}^{ническая скорость – 40 км/час, а суммарное время под погрузкой-разгрузкой – 20 минут.}

Так как договора заключаются с каждым потребителем отдельно, в этой связи для каждого потребителя требуется определить необходимое количество автомобилей для его обслуживания, а также путь, который проходит это количество автомобилей.

Для обслуживания потребителя, например, за 8-ми часовой рабочий день может потребоваться один и более автомобилей. Поэтому, во-первых, необходимо определить то количество автомобилей, которое нужно для обслуживания потребителя за время работы в наряде (8 часов) по формуле:

(1)
Полученное количество автомобилей округляется в большую сторону до целого числа.

Так, необходимое количество автомобилей для первого потребителя (П1) составит: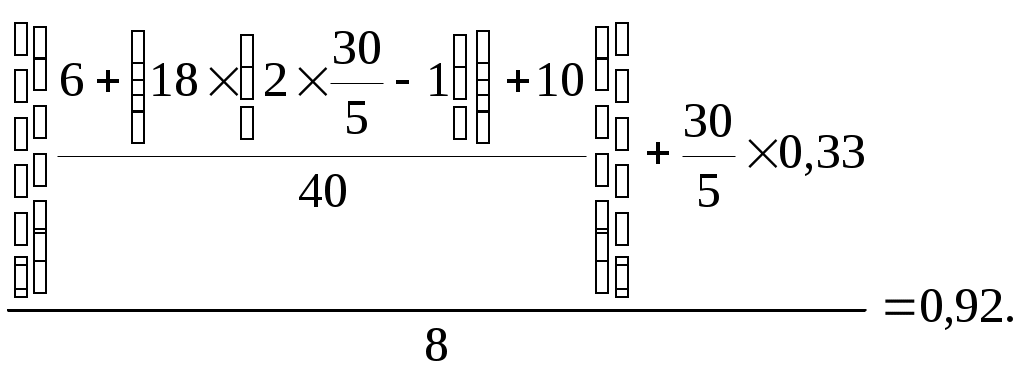

Рассчитанное дробное число (0,92) округляется в большую сторону до целого числа – 1 автомобиль.

Необходимое количество автомобилей для второго потребителя (П2):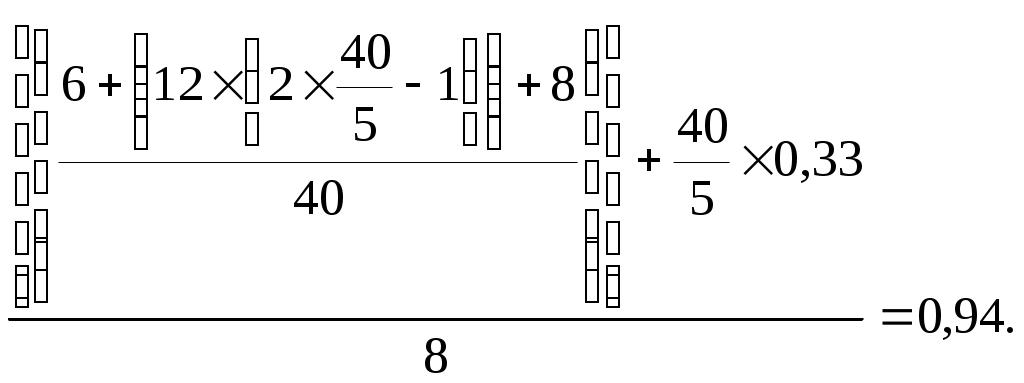

Рассчитанное дробное число (0,94) округляется в большую сторону до целого числа – 1 автомобиль.

Необходимое количество автомобилей для третьего потребителя (П3):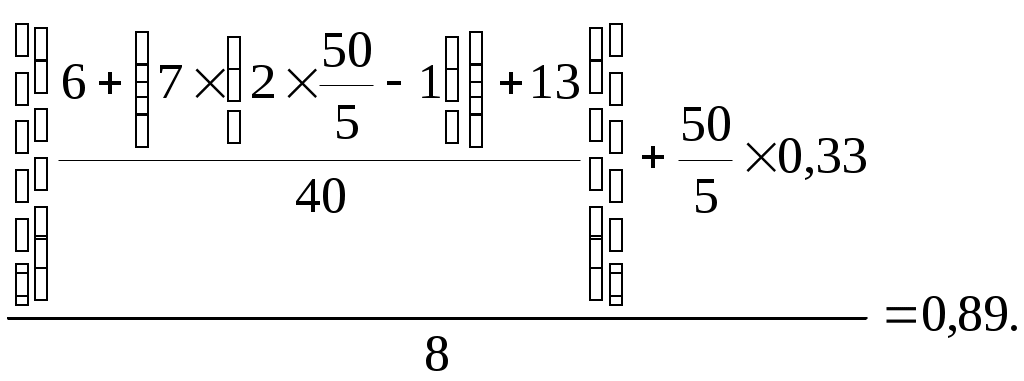

Рассчитанное дробное число (0,89) округляется в большую сторону до целого числа – 1 автомобиль.

Путь, который проходят автомобили (полученное количество автомобилей) при обслуживании соответствующего потребителя определяется по следующей формуле: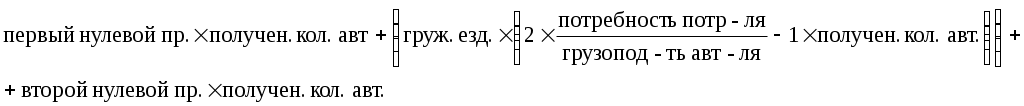

(2)
Так, путь, который проходит полученное количество автомобилей (1 автомобиль) для обслуживания первого потребителя составит:

.
Путь, который проходит полученное количество автомобилей (1 автомобиль) для обслуживания второго потребителя составит:

.
Путь, который проходит необходимое количество автомобилей (1 автомобиль) для обслуживания третьего потребителя составит:

.
^{Результаты представленных выше расчетов отмечаются в соответствующих договорах на обслуживание потребителей и являются исходной базой для расчета стоимости транспортных услуг для каждого из потребителей. Таким образом, совокупный дневной пробег автомобилей по обслуживанию трех потребителей согласно договорам составит 560 км (214+194+152км).}

^{Задача оптимизации транспортных маршрутов состоит в том, чтобы обеспечить минимально необходимый пробег автомобилей при обслуживании потребителей. Анализ исходной информации и рисунка 2 показывает, что совокупный груженый пробег автомобилей оптимизировать невозможно, так как количество ездок, которое необходимо сделать потребителям, а также расстояния от карьера до пунктов назначения строго зафиксированы договорными обязательствами. Следовательно, оптимизация маятниковых маршрутов возможна только за счет минимизации совокупного порожнего пробега. Это достигается, одновременно учитывая второй нулевой и холостой пробеги автотранспорта для соответствующих потребителей. Так, например, в нашем примере потребитель П}₂^{отличается минимальным вторым нулевым пробегом (8 км). Однако, максимальный холостой пробег имеет место при обслуживании потребителя П}₃^{(холостой пробег = груженой ездке = 18 км). В этой связи, чтобы учесть влияния этих двух показателей необходимо определить их разность для всех потребителей.}

^{Таким образом, минимизация совокупного порожнего пробега возможна в случае выполнения следующих двух условий:}

^{1. Построение маршрутов по обслуживанию потребителей (пунктов назначения) необходимо осуществлять таким образом, чтобы на пункте назначения, который имеет минимальную разность расстояния от него до автотранспортного предприятия и расстояния от товарной базы (в нашем случае, карьера) до этого пункта назначения (разность второго нулевого пробега и груженой ездки), заканчивало свою дневную работу, возвращаясь на автотранспортное предприятие, максимально возможное число автомобилей. При этом данное максимальное число определяется количеством ездок, которое необходимо сделать в этот пункт назначения. Так, если общее число автомобилей по обслуживанию всех потребителей равно или меньше количества ездок, которое необходимо сделать в указанный пункт назначения, то все эти автомобили проедут через данный пункт назначения, сделав последнюю груженую ездку в конце рабочего дня при возвращении на АТП. В противном случае, если общее число автомобилей по обслуживанию всех потребителей больше количества ездок, которое необходимо сделать в указанный пункт назначения, то автомобили, которые входят в превышающее число, должны оканчивать свою дневную работу на пункте назначения, имеющем следующее по величине минимальное значение разности второго нулевого пробега и груженой ездки и т.д.}

^{2. Общее число автомобилей, работающих на всех маршрутах при обслуживании потребителей, должно быть минимально необходимым. Это достигается обеспечением максимально полной загрузки автомобилей по времени в течение рабочего дня (например, восьмичасовой рабочей смены).}

^{С учетом вышепредставленных условий запишем структурную математическую модель оптимизации маятниковых маршрутов:}

^{при условиях:}

^где^L^{– совокупный порожний пробег, км;}

^j^{– номер потребителя;}

ⁿ

– расстояние от пункта назначения (П_j) до автотранспортного предприятия (второй нулевой пробег), км;

^{– количество потребителей;}
^l_КП_j^–^{расстояние от товарной базы (в нашем случае, карьера}^{К) до пункта назначения (П}_j^{) (груженая ездка), км;}

^X_j^{– количество автомобилей, работающих на маршрутах с последним пунктом разгрузки (П}_j^);

^Q_j^{– необходимое количество ездок в пункт назначения (П}_j^);

^N^{– общее число автомобилей, работающих на всех маршрутах.}

^{Применяется следующий алгоритм решения подобных задач.}

^{Составляется рабочая матрица № 1 (таблица 1).}

^{Таблица 1 – Исходная рабочая матрица № 1}

^{Пункт назначения}	^{Исходные данные}	^{Оценка (разность расстояний)}
^П_j	^l₀^П^j^l_КП_j ^Q_j	^l₀^П^j^–^l_КП_j
^П₁	^{10 18} ⁶	^-8
^П₂	^{8 12} ⁸	^-4
^П₃	^{13 7} ¹⁰	⁶

^{Выбирают пункт, имеющий минимальную оценку (разность расстояний). В нашем примере – это пункт назначения П}₁^.

^{2. Учитывая исходную информацию (двухсторонние договора), предварительно принимается общее число автомобилей (}^N^{), работающих на всех маршрутах по обслуживанию потребителей П}₁^{, П}₂^{и П}₃^{(в нашем примере равно трем). Следует подчеркнуть, что в результате оптимизационных расчетов число (}^N^{) может остаться на прежнем уровне или сократиться.}

^{3. В соответствии с первым условием обеспечения минимизации совокупного порожнего пробега устанавливается количество автомобилей, которое проедет через выбранный пункт назначения (см. п. 1 алгоритма), осуществляя последнюю груженую ездку в конце рабочего дня при возвращении на АТП. В нашем примере этот пункт назначения П}₁^{. При этом, так как общее число автомобилей по обслуживанию потребителей П}₁^{, П}₂^{и П}₃^{равно трем (меньше необходимого количества ездок, которое необходимо сделать в пункт назначения П}₁^{, в два раза) следовательно, на данном пункте будут оканчивать свою дневную работу все три автомобиля, осуществляя в пункт П}₁^{по две груженые ездки.}

^{Так как в пункты назначения П}₂^{и П}₃^{необходимо сделать четное число ездок 8 и 10 соответственно (не делится поровну на каждый из трех автомобилей), очевидно, что каждый из автомобилей будет двигаться по собственному маршруту или один из них – по одному маршруту, а два других – по другому.}

^{4. Определяется маршрут движения для первого автомобиля. Для этого выбирают два пункта, имеющих минимальную и наибольшую оценку (разность расстояний). В нашем случае это соответственно –8 (П}₁^{) и 6 (П}₃^{). Исходя из первого условия, автомобиль, обслуживающий эти пункты назначения начинает рабочую смену с пункта П}₃^{и заканчивает пунктом П}₁^.

^{5. Определяется, какое количество груженых ездок сможет сделать автомобиль в пункты назначения первого маршрута за восьмичасовой рабочий день.}

^{Из вышепредставленных рассуждений (см. п. 3 алгоритма) в пункт назначения П}₁^{будет сделано две груженые ездки. В этой связи остается определить, сколько ездок осуществит автомобиль в пункт П}₃^.

^{Для этого рассчитывают поминутное время работы первого автомобиля на маршруте.}

^{Время в пути от Г до К = (}^l_ГК^/^υ_т^{) · 60 мин. = (6/40) · 60 = 9 мин.}

^{Время в пути от П}₁^{до Г = (10/40) · 60 = 15 мин.}

^{Время оборота КП}₃^{К = ((7 + 7)/40) · 60 + 20 = 41 мин.}

^{Время в пути КП}₁^КП₁^{= (18·3/40) · 60 + 20·2 = 121 мин.}

^{Где 20 минут – это суммарное время под погрузкой-разгрузкой.}

^{Определяем, сколько ездок сделает автомобиль в пункт П}₃^{, учитывая, что время его работы в наряде составляет 480 мин.}
^{(480 – 9 – 121 – 15)/41 = 8 ездок.}
^{6. Цикл повторяется. Составляется вторая рабочая матрица с учетом выполненной работы на первом маршруте. В нашем примере в пункт назначения П}₁^{сделано 2 ездки, а в пункт П}₃^{– 8 ездок (таблица 2).}
^{Таблица 2 – Рабочая матрица № 2}

^{Пункт назначения}	^{Исходные данные}	^{Оценка (разность расстояний)}
^П_j	^l₀^П^j^l_КП_j ^Q_j	^l₀^П^j^–^l_КП_j
^П₁	^{10 18} ^{4 = 6 – 2}	^-8
^П₂	^{8 12} ⁸	^-4
^П₃	^{13 7} ^{2 = 10 – 8}	⁶

^{7. Определяется маршрут движения для второго автомобиля. В нашем примере (принимая во внимание пункты 3 и 4 алгоритма), очевидно, что маршрут движения второго автомобиля будет проходить через все три пункта назначения: в начале рабочего дня второй автомобиль сделает две ездки в пункт П}₃^{(таким образом, дообслужив его), начнет обслуживание пункта П}₂^{и также как первый автомобиль сделает в конце рабочего дня две груженые ездки в пункт П}₁^{и возвратиться на АТП. Из этого следует, что необходимо определить, сколько ездок осуществит (успеет осуществить) второй автомобиль в пункт П}₂^.

^{Рассчитаем поминутное время работы на маршруте движения второго автомобиля.}

^{Время в пути от Г до К = (6/40) · 60 = 9 мин.}

^{Время в пути от П}₁^{до Г = (10/40) · 60 = 15 мин.}

^{Время двух оборотов КП}₃^{К = 2· [((7 + 7)/40) · 60 + 20] = 82 мин.}

^{Время оборота КП}₂^{К = ((12 + 12)/40) · 60 + 20 = 56 мин.}

^{Время в пути КП}₁^КП₁^{= (18·3/40) · 60 + 20·2 = 121 мин.}

^{Определяем, сколько ездок сделает второй автомобиль в пункт П}₂^{, учитывая, что время его работы в наряде составляет 480 мин.}
^{(480 – 9 – 82 – 121 – 15)/56 = 4 ездки.}
^{8. Цикл повторяется. Составляется третья рабочая матрица с учетом выполненной работы на первом и втором маршрутах. В нашем примере в пункт назначения П}₁^{сделано 4 ездки, в пункт П}₃^{– 10 ездок (дневные потребности удовлетворены), а в пункт П}₂^{– 4 ездки (таблица 3).}
^{Таблица 3 – Рабочая матрица № 3}

^{Пункт назначения}	^{Исходные данные}	^{Оценка (разность расстояний)}
^П_j	^l₀^П^j^l_КП_j ^Q_j	^l₀^П^j^–^l_КП_j
^П₁	^{10 18} ^{2 = 6 – 4}	^-8
^П₂	^{8 12} ^{4 = 8 – 4}	^-4

^{9. Определяется маршрут движения для третьего автомобиля. Анализ таблицы 7.3 показывает, что его маршрут движения будет проходить через пункты назначения}^П₂^{и П}₁^{: в начале рабочего дня третий автомобиль сделает 4 ездки в пункт}^П₂^,^{и также как первый и второй автомобили сделает в конце рабочего дня две груженые ездки в пункт П}₁^{и возвратиться на АТП.}

^{Сравнивая маршрут движения третьего автомобиля с маршрутом движения второго, можно с уверенностью сказать, что третий автомобиль будет иметь определенную недогрузку по времени рабочей смены. Определим ее величину, для чего рассчитаем поминутное время работы на маршруте движения третьего автомобиля.}

^{Время в пути от Г до К = (6/40) · 60 = 9 мин.}

^{Время в пути от П}₁^{до Г = (10/40) · 60 = 15 мин.}

^{Время четырех оборотов КП}₂^{К = 4· [((12 + 12)/40) · 60 + 20] = 224 мин.}

^{Время в пути КП}₁^КП₁^{= (18·3/40) · 60 + 20·2 = 121 мин.}

^{Величина недогрузку по времени рабочей смены третьего автомобиля составит:}
^{480 – 9 – 224 – 121 – 15 = 111 мин. ≈ 2 часа.}
^{Величина недогрузку по времени рабочей смены третьего автомобиля позволяет при необходимости направить последнего на выполнение другой транспортной работы.}

^{10. Составляется сводная маршрутная ведомость (таблица 4).}
^{Таблица 4 – Сводная маршрутная ведомость}

^№^{маршрута}	^{Последовательность} ^{выполнения маршрута}	^{Расшифровка}	^{Количество} ^{автомобилей} ^{на маршруте}	^Длина ^{маршрута, км}
¹	^{Г→(К→П}₃^{→К)·8→П}₁^→ ^→К→П₁^→Г	^{Г – АТП} ^{К – карьер} ^П₃^{– ПМК} ^П₁^{– ЖБИ}	¹	¹⁸²
²	^{Г→(К→П}₃^{→К)·2→П}₂^→ ^→^К→П₂^→К→П₂^→К→ ^→П₂^→К^→П₁^→К→П₁^→Г	^{Г – АТП} ^{К – карьер} ^П₃^{– ПМК} ^П₂^{– РСУ} ^П₁^{– ЖБИ}	¹	¹⁹⁴
³	^{Г→(К→П}₂^{→К)·4→П}₁^→ ^→К→П₁^→Г	^{Г – АТП} ^{К – карьер} ^П₂^{– РСУ} ^П₁^{– ЖБИ}	¹	¹⁶⁶

^{8, 2 и 4 – количество оборотов.}
^{Анализ таблицы 4 показывает, что совокупный дневной пробег трех автомобилей в соответствии с проведенными оптимизационными расчетами составляет 542 км, что на 18 км (560 – 542 км) меньше по сравнению с традиционным порядком обслуживания (до оптимизации).}

1 2