ПиАХТ. Основы гидродинамики. ПИАХТ практическая работа 2. Программа профессиональной переподготовки Химическая технология природных энергоносителей и углеродных материалов Расчетное задание по теме Основы гидродинамики
 Скачать 115.67 Kb.
|
|
Министерство образования и науки Российской федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Институт дополнительного профессионального образования Программа профессиональной переподготовки «Химическая технология природных энергоносителей и углеродных материалов» Расчетное задание по теме: «Основы гидродинамики» Вариант 3 Задачи № 1, 2, 5, 8, 9, 10, 11 по дисциплине «Процессы и аппараты химической технологии» Слушатель гр. ТПД(ДОТ)-21-01 _________________ А.Р. Беломоина подпись, дата Преподаватель _________________ О.В. Ишалина подпись, дата Уфа 2021 Задача 2.1. Манометр на трубопроводе, заполненном жидкостью, показывает давление 0,18 кгс/см2. На какую высоту h над точкой присоединения манометра поднимется в открытом пьезометре жидкость, находящаяся в трубопроводе, если эта жидкость: а) вода, б) четыреххлористый углерод (CCl4). Решение. Высота уровня жидкости в резервуаре над точкой присоединения манометра определяется уравнением: 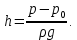 Манометр на трубопроводе показывает избыточное давление: 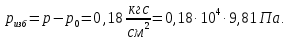 Плотность воды и четыреххлористого углерода найдем в таблице А.4 (Приложение А): а) 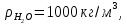 б) 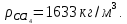 Подставив известные данные в уравнение, найдем высоту уровня жидкости в резервуаре над точкой присоединения манометра: а) 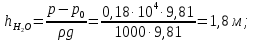 б) 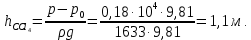 Задача 2.2. Холодильник состоит из 19 труб диаметром 20×2 мм. В трубное пространство холодильника поступает вода по трубопроводу диаметром 57×3,5 мм. Скорость воды в трубопроводе 1,4 м/с. Вода идет снизу вверх. Определить скорость воды в трубах холодильника. Решение. Скорость воды в трубах холодильника определяется из уравнения: 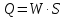 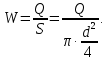 Определим расход воды из трубопровода в холодильник применяя тоже уравнение: 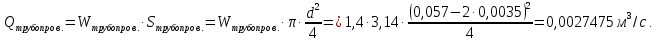 Так как вода подается снизу вверх и распределяется равномерно по трубкам холодильника, то в каждой из трубок будет 1/19 части расхода воды из трубопровода: 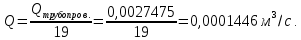 Подставим найденные значения в уравнение для расчета скорости воды в трубках холодильника: 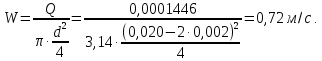 Задача 2.5. Вычислить в общей форме гидравлический радиус при заполненном сечении для кольцевого сечения, квадрата, прямоугольника и равностороннего треугольника. Решение. Формула для определения гидравлического радиуса: 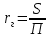 где S – площадь сечения потока жидкости, м2; П – смоченный периметр, м. Выведем формулу для определения гидравлического радиуса кольцевого сечения: 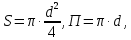 где d – диаметр сечения, м; 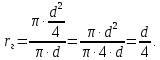 Выведем формулу для определения гидравлического радиуса квадратного сечения: 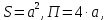 где a – сторона сечения, м; 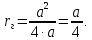 Выведем формулу для определения гидравлического радиуса прямоугольного сечения: 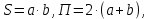 где aи b – неравные стороны сечения, м; 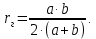 Выведем формулу для определения гидравлического радиуса сечения формой равностороннего треугольника: 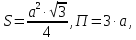 где a – сторона сечения, м; 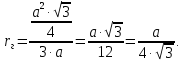 Задача 2.8. Определить режим течения этилового спирта: а) в прямой трубе диаметром 40×2,5 мм; б) в змеевике, свитом из той же трубы. Диаметр витка змеевика 570 мм. Скорость спирта 0,13 м/с, средняя температура 52 °C. 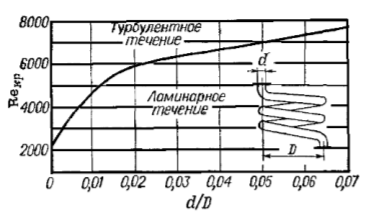 Рис.1 Решение. Примем, что концентрация этилового спирта составляет 10%. Для определения режима движения жидкости необходимо вычислить критерий Рейнольдса: 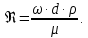 А) Для определения плотности этилового спирта при температуре 52 °C с применением метода линейной интерполяции найдем по таблице А.4 в приложении А плотности этилового спирта при температурах 40 °C и 60 °C: 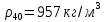 , 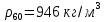.Применяя формулу линейной интерполяции, получим: 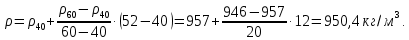 Для определения коэффициента динамической вязкости этилового спирта при температуре 52 °C с применением метода линейной интерполяции найдем по рисунку Б.1 в приложении Б коэффициенты динамической вязкости этилового спирта при температурах 40 °C и 60 °C: 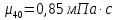 , 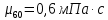.Применяя формулу линейной интерполяции, получим: 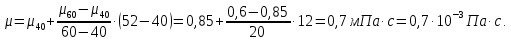 Определим критерий Рейнольдса: 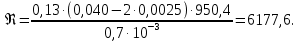 Критерий Рейнольдса находится в пределах 2320 < 6177,6 < 10000, что говорит нам о неустойчиво турбулентном (переходном) режиме движения жидкости. Б) Для потоков жидкостей, проходящих по изогнутым трубам, критическое значение критерия Рейнольдса зависит от отношения диаметра трубы к диаметру витка. Используя график (рис.1) определим режим течения жидкости в змеевике, свитом из той же трубы. Найдем значение 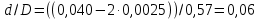 .Из графика видно, что при 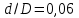 критическое значение критерия Рейнольдса составляет примерно 7300. До этого значения режим течения считается ламинарным, после – турбулентным. В нашем случае, при значении 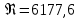 , режим течения этилового спирта будет ламинарным, т.к. 6177,6 < 7300.Задача 2.9. Определить местную скорость по оси трубопровода диаметром 57×3,5 мм при протекании по нему уксусной кислоты в количестве 200 дм3/ч при 38 °С. Решение. Примем, что концентрация уксусной кислоты 100%. Для нахождения скорости по оси трубопровода, т.е. максимальной скорости потока, определим режим движения жидкости по трубопроводу. Найдем критерий Рейнольдса 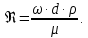Для определения плотности уксусной кислоты при температуре 38 °C с применением метода линейной интерполяции найдем по таблице А.4 в приложении А плотности уксусной кислоты при температурах 20 °C и 40 °C: 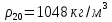 , 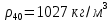.Применяя формулу линейной интерполяции, получим: 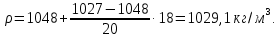 Для определения коэффициента динамической вязкости уксусной кислоты при температуре 38 °C с применением метода линейной интерполяции найдем по рисунку Б.1 в приложении Б коэффициенты динамической вязкости этилового спирта при температурах 30 °C и 50 °C: 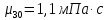 , 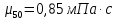.Применяя формулу линейной интерполяции, получим: 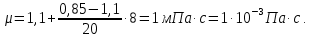 Определим среднюю скорость движения жидкости используя формулу: 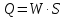 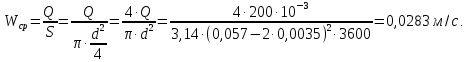Подставим найденные в уравнение: 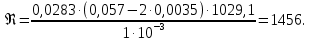 Значение критерия Рейнольдса 1456<2320, следовательно, режим движения жидкости ламинарный. При ламинарном движении жидкости 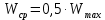 .Т.к. максимальная скорость потока проходит по оси трубопровода, то: 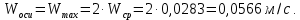 Задача 2.10. В середине трубопровода с внутренним диаметром 320 мм установлена трубка Пито—Прандтля (рисунок 2), дифференциальный манометр которой, заполненный водой, показывает разность уровней Н = 5,8 мм. По трубопроводу проходит под атмосферным давлением сухой воздух при 21 °С. Определить массовый расход воздуха. 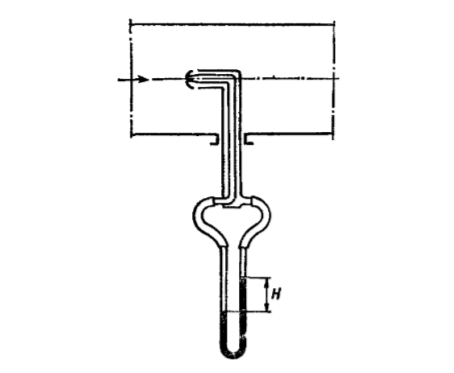 Рис. 2 Решение. Массовый расход определяется уравнением: 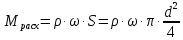 Плотность воздуха при атмосферном давлении и 21 °C: 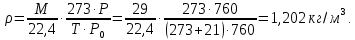 Необходимо найти среднюю скорость движения воздуха. Воспользуемся графиком на рисунке 3. 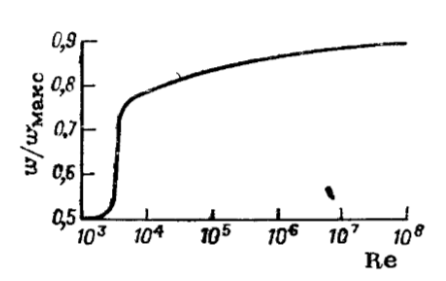 Рис. 3 Т.к. трубка Пито—Прандтля установлена по оси трубопровода максимальная скорость воздуха определяется из формулы: 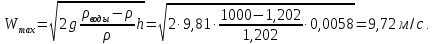 Найдем критерий Рейнольдса: 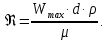 Для этого определим коэффициент динамической вязкости воздуха при температуре 21 °C методом линейной интерполяции используя номограмму из приложения Б (рисунок Б.2): 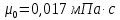 , 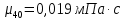.Применяя формулу линейной интерполяции, получим: 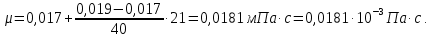 Подставив известные значения, найдем критерий Рейнольдса для потока воздуха в трубопроводе: 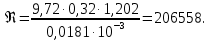 По графику на рисунке 3 видно, что 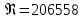 соответствует отношение  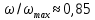Следовательно, в нашем расчете средняя скорость потока: 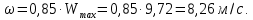 Найдем массовый расход воздуха подставив в уравнение известные значения: 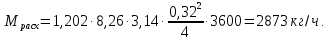 Задача 2.11. Из отверстия диаметром 10 мм в дне открытого бака, в котором поддерживается постоянный уровень жидкости высотой 900 мм, вытекает 750 дм3 жидкости в 1 ч. Определить коэффициент расхода. Через сколько времени опорожнится бак, если прекратить подачу в него жидкости? Диаметр бака 800 мм. Решение. Коэффициент расхода жидкости определим из уравнения расхода: 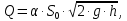 где S0 – площадь сечения отверстия в дне бака. 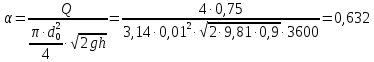 где d0 – диаметр отверстия в дне бака. Определим время истечения жидкости по формуле: 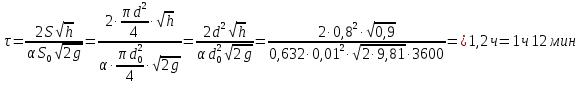 где S – площадь сечения бака, d – диаметр бака. |