Задание 3_Лейченко Ю.С.. Программа среднего профессионального образования Право и организация социального обеспечения Дисциплина Математика
 Скачать 26.79 Kb. Скачать 26.79 Kb.
|
|
Автономная некоммерческая организация профессионального образования «Открытый социально- экономический колледж» Программа среднего профессионального образования Право и организация социального обеспечения Дисциплина: Математика Практическое задание № 3 Выполнил: слушатель: Лейченко Юлия Сергеевна Преподаватель: Васильцова Анна Сергеевна Задание №1 1. В домашней библиотеке у Василия Петровича собрано 34 книги по научной фантастике. Он хочет взять с собой в отпуск 2 книги для чтения. Сколькими способами Василий Петрович может это сделать? 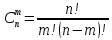 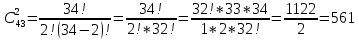 Ответ: 561. 2. В кино отправились 5 друзей. Сколькими разными способами они могут встать в очередь на кассе? 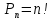 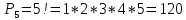 Ответ: 120. 3. Таблица, размером 99*99, раскрашена в шахматном порядке в белый и черный цвета. Верхняя левая клетка – белая. Сколькими способами можно указать в таблице два квадрата – белый и черный? Белых клеток в таблице на 1 больше, т.к. верхняя клетка белая. 99*99=9801 клеток в таблице. (9801-1)/2=4900 – черные клетки. 4900+1=4901 – белые клетки. 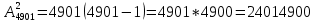 Ответ: 24014900. Задание №2 1. При игре в кости бросаются два игральных кубика и подсчитывается сумма выпавших очков. Найти вероятность событий: А – сумма равна 4; В – сумма больше 7. Число всевозможных подбрасывания кубиков: п = 6 • 6 = 36. Исходы будем представлять как упорядоченные пары чисел вида (х,у), где число выпадения очков на первой кости, у число выпадения очков на второй кости. Найдём все исходы: сумма выпавших очков равна 4 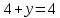 (1;3), (2; 2), (3; 1). - m = 3 благоприятных исходов A. (1;3), (2; 2), (3; 1). - m = 3 благоприятных исходов A.Вероятность события А: 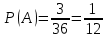 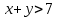 (2;6), (3; 6), (4; 6), (5; 6), (6; 6), (3; 5), (4; 5), (4; 4), (5; 5), (5; 4), (5; 3), (6; 5), (6; 4), (6; 3), (6; 2) - m = 15 благоприятных исходов B. Вероятность события В: 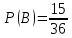 Ответ: Ответ: 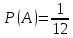 ; ; 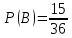 . .2. Из имеющихся 20 телевизоров 14 готовы к продаже, а 6 требуют дополнительной регулировки. Найти вероятности событий: А – из случайно отобранных 4 телевизоров все хорошие, В – три хорошие и один нет, С – один хороший и три нет, D – хороших нет. 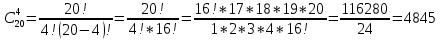 1) Вероятность события А: 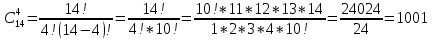 Искомая вероятность: 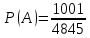 2) Вероятность события В: 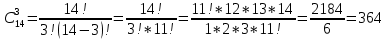 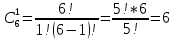 По правилу произведения, всего таких способов: 364*6 = 2184 Искомая вероятность: 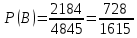 3) Вероятность события C: 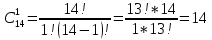 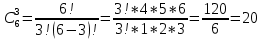 По правилу произведения, таких способов 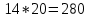 Искомая вероятность: 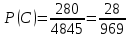 4) Вероятность события D: 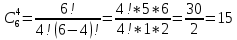 Искомая вероятность: 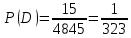 Ответ: 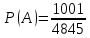 , , 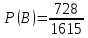 , , 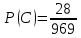 , , 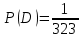 . .3. Туристическая группа состоит из 11 юношей и 5 девушек. По жребию (случайным образом) выбирают 3 дежурных. Найти вероятность того, что будут выбраны 2 девушки и 1 юноша. 11+ 5=16 -всего человек. 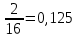 - вероятность, что будет выбраны две девушка. - вероятность, что будет выбраны две девушка. 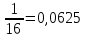 - вероятность, что будет выбран 1 юноша. - вероятность, что будет выбран 1 юноша. Тула – 2023 |
