лаба 7.2 вариант 24. Программирование алгоритмов вложенных циклических структур
 Скачать 137.81 Kb. Скачать 137.81 Kb.
|
|
Федеральное агентство связи Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» Кафедра информатики ЛАБОРАТОРНАЯ РАБОТА № 7.2 по дисциплине “Информатика” на тему «Программирование алгоритмов вложенных циклических структур» Выполнил: студент гр. Проверил: Москва 2021 г. Оглавление Задание на разработку проекта и вариант задани ….…………….……....3 Схемы алгоритмов…………………………………………………………...4 Программный код ………………………………….………………………..6 Результаты выполнения проектов……………….…….……………...…...9 Доказательство правильности……………………………………………..9 1.Задание на разработку проекта и вариант задания Создать приложение (решение), состоящее из трех проектов с именем Lab7 в соответствии с общим заданием для вычисления функции с условием l=f(a,x )(Рисунок 1)  Рисунок 1 – Задание 2. Схемы алгоритмов Схема Main()(Рисунок 2) 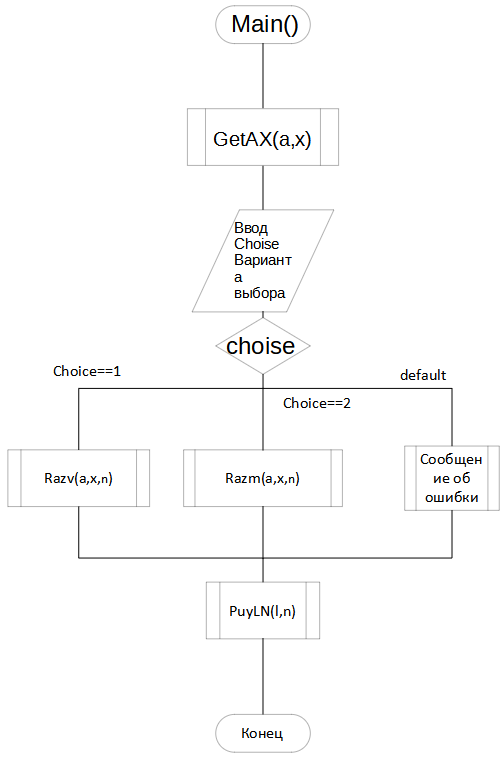 Рисунок 2- Схема алгоритма главной функции main() Схема Ввода и вывода (Рисунок 3) 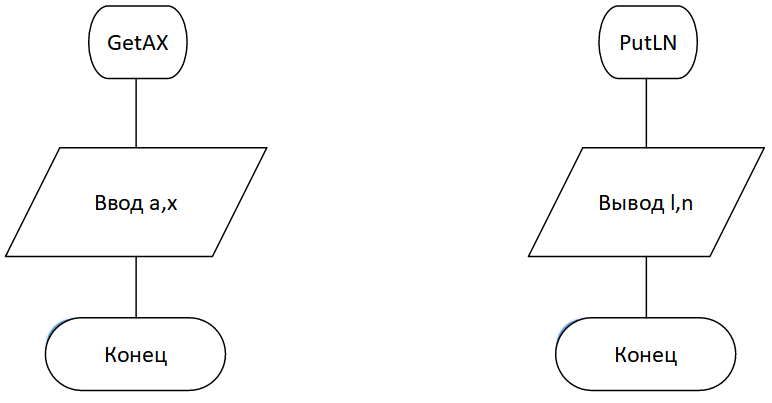 Рисунок 3 - Схемы алгоритмов функций GetABXY и PutPN Схема Razv() (Рисунок 4 ) 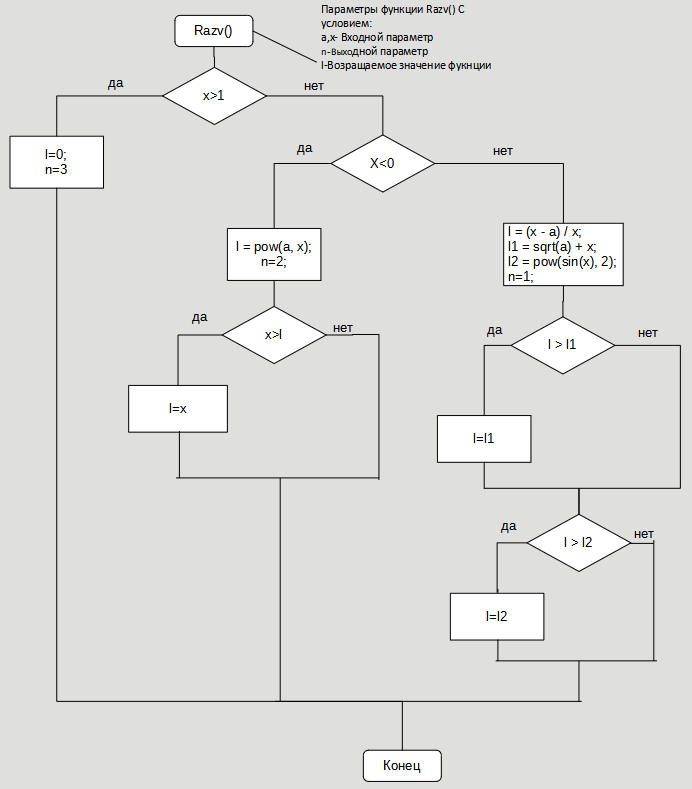 Рисунок 4-схема функции Razv() Схема Razv2() (Рисунок 5) 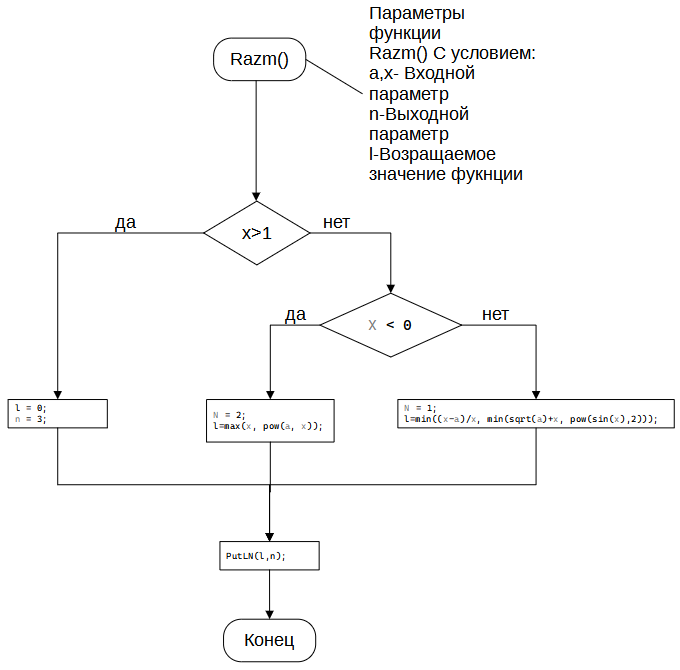 Рисунок 5-схема функции Razm() 3. Код программы Главный файл: // Файл main1.cpp #include #include using namespace std; void GetAX(double& a, double& x); void PutLN(double, int); double Razv(double a, double x, int& n); double Razm(double a, double x, int& n); int main() { double a, x, l; int n; // Номер ветки GetAX(a, x); // Вызов функции ввода исходных данных int choice; // Вариант выбора решения cout << " Каким способом решать задачу?\n"; cout << " 1 - с вложенными разветвлениями "; cout << " без библиотечных функций max и min \n "; cout << " 2 - со своими функциями minMy и maxMy \n "; cout << " Что выбираете 1 или 2 ?\n "; cin >> choice; switch (choice) { case 1: l = Razv(a, x, n); break; case 2: l = Razm(a, x, n); break; default: cout << "Ввод выполнен неправильно! "; cout << endl; system("PAUSE"); return 0; } PutLN(l, n); // Вызов функции вывода результатов system("PAUSE"); return 0; } Файл с вводом и выводом: // Файл GetPut.cpp с функциями ввода и вывода #include using namespace std; // Определение функции ввода void GetAX(double& a, double& x) { setlocale(LC_ALL, "rus"); cout << " Введите a, x\n "; cin >> a >> x; } // Определение функции вывода void PutLN(double l, int n) { setlocale(LC_ALL, "rus"); cout << " Вычислено значение сложной функции д = " << l << endl; cout << " Номер ветки разветвления n = " << n << endl; } Файл без доп. функций мин. и макс и c доп. функций мин. и макс: // Файл Raz с функциями Razv, Razm #include #include using namespace std; // Определение ф-ции с вложенными разветвлениями и без функций max и min double Razv(double a, double x, int& n) { double l; // Локальная переменная ФУНКЦИИ if (x >1) { l = 0; n = 3; } else if (x < 0) { l = pow(a, x); if (x > l) l =x; n = 2; } else { l = (x-a)/x; double l1 = sqrt(a)+x; double l2 = pow(sin(x),2); if (l > l1) l = l1; if (l > l2) l = l2; n = 1; } return l; } // Описания (прототипы) ф-ций maxMy и minMy double max(double x, double y); double min(double x, double y); //Определение ф-ции с вложенными разветвлениями, использующей maxMy и minMy double Razm(double a, double x, int& n) { if (x > 1) { n = 3; return 0; } else if (x < 0) { n = 2; return max(x, pow(a, x)); } else { n = 1; return min((x - a) / x, min(sqrt(a) + x, pow(sin(x), 2))); } } // Определение функций maxMy double max(double x, double y) { double f; if (x > y) f = x; else f = y; return f; } // Определение функций minMy double min(double x, double y) { double f; if (x < y) f = x; else f = y; return f; } 4. Результат выполнения проектов Консольная отладка для 3 проекта (Рисунок 6) 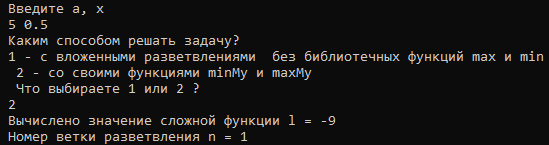 Рисунок 6- Консольная отладка для 3 проекта 5.Доказательство правильности работы программы Таблица 1 – таблица данных
Доказательство по веткам разветвления(для подcчёта берутся значения из таблицы 1): Для первой строки x∈[0;1],тогда вычисления идут по первой ветви и находится l=min((x - a) / x, sqrt(a) + x, (sin(x))^2)= min((0.5 - 5) / 0.5, sqrt(5) + 0.5, (sin(0.5))^2)=min(-9,2.23607+0.5,0.22985), l=-9 – верно Для второй строки x<0 ,тогда вычисления идут по второй ветви и находится вычисления l= max(x,a^x)=max(5,5^(-5)), l=0.00032- верно Для третий строки ,заданы вычисления третьей ветви и находится вычисления l=0,l=0-верно Вывод: при тестовых данных результаты ручного расчёта и вычисления на компьютере совпадают. | ||||||||||||||||||||||||
