Математика_Контрольная_Интегральное исчисление. Решение_Математика_Интегралы_1_7_11. Простейшие дроби Данко, Попов (ч. 1) стр. 218
 Скачать 1.08 Mb.
|
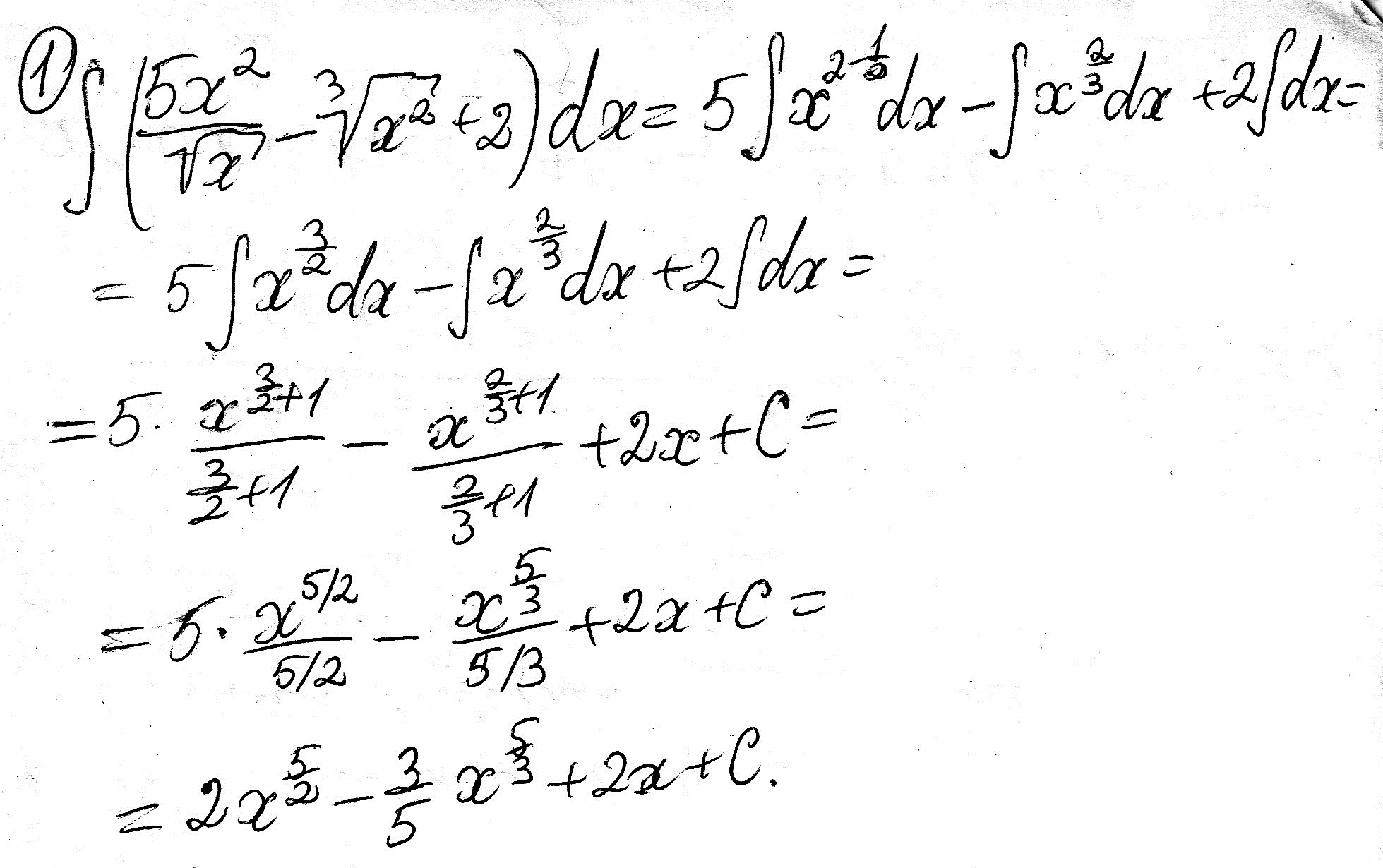  11.  . Простейшие дроби: Данко, Попов (ч.1) – стр. 218. Подынтегральная функция – рациональная дробь. Интегрируем с помощью разложения на простейшие дроби. Множителю  соответствует сумма простейших дробей: , а множителю  – простейшая дробь  . Итак,  .Освободимся от знаменателя:  .Действительными корнями знаменателя являются числа 0 и -2. Полагая  , получаем  , т.е. .При  имеем:  , т.е.  .Сравним теперь коэффициенты при старшей степени , т.е. при  . В левой части коэффициент при равен 1, в правой части коэффициент при равен  . Итак, . Откуда  .Для определения коэффициента  придадим значение  . Получаем уравнение: . Отсюда  Для проверки придадим значение  . Имеем:  .Получили верное равенство. Значит, вычисления числителей простейших дробей выполнены правильно. Окончательное разложение подынтегральной дроби на простейшие имеет вид:  .Таким образом, получим  17.  19. 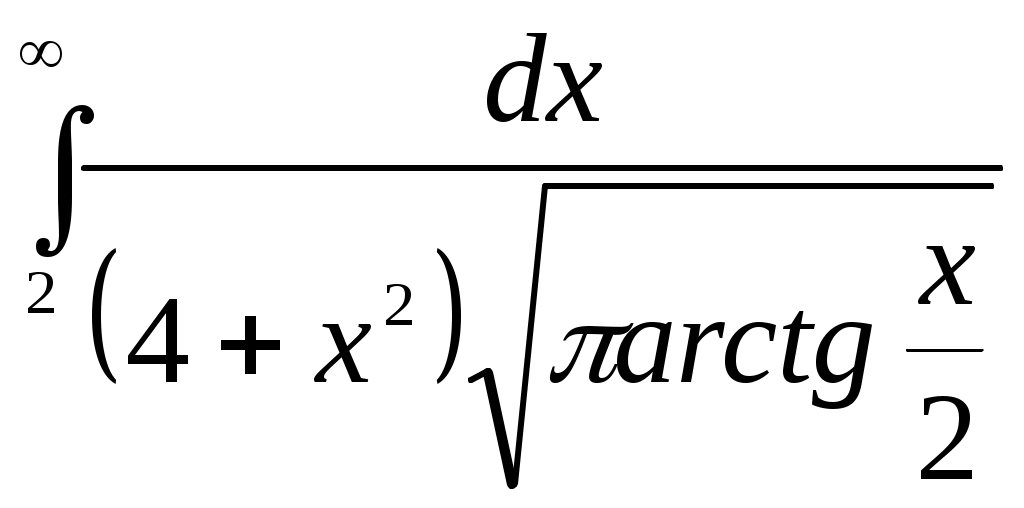 |