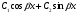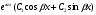Шифр навчального
елементу
|
Базове тестове завдання
|
Правильна
відповідь
| Шифр базового
тестового завдання
| бали |
ХХ..01.01
Визначники. Елементи теорії матриць.
|
Знайти суму матриць 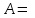 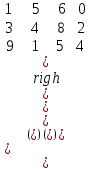 і і 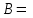 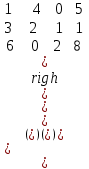 . .
А.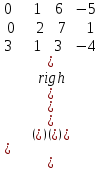
B.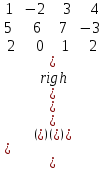
С. 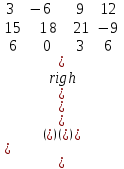
D.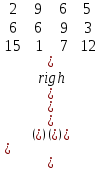 . .
|
D
|
ХХ..01.01.А.ПА 01
|
2
|
ХХ..01.01
|
Знайти різницю матриць 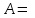 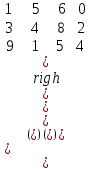 і і 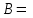 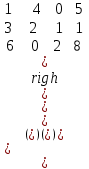 . .
А. .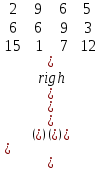
B. 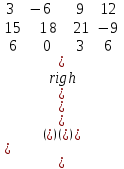
С. 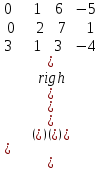
D. 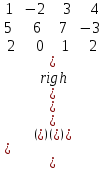
|
C
|
ХХ..01.01.А.ПА 02
|
2
|
ХХ..01.01
|
Знайти добуток матриць:
а) 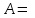 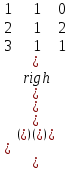 ; ;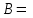 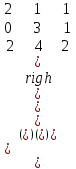 ; ;
А. 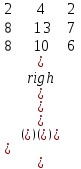
B. 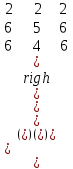
С. 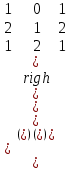
D. 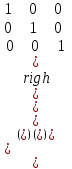
|
A
|
ХХ..01.01.А.ПА 03
|
2
|
ХХ..01.01
|
Обчислити визначник третього порядку:
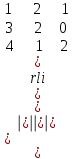 . .
А. 10
B. –13
С. 4
D. -7
|
B
|
ХХ..01.01.А.ПА 04
|
2
|
ХХ..01.01
|
Обчислити визначник третього порядку:
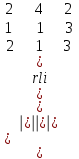 . .
А. 10
B. 43
С. 32
D. 0
|
A
|
ХХ..01.01.А.ПА 05
|
2
|
ХХ..01.03
Елементи векторної алгебри.
|
Задано точки А(1,3,1), В(-1,4,6), С(-2,-3,4). Знайти скалярний добуток векторів 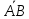 і і 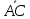
A.3
B.27
C.15
D.-12
|
С
|
ХХ..01.03.А.ПА.01
|
2
|
ХХ..01.03
|
Задано точки А(6,1,1), В(4,6,6), С(4,2,0). Знайти скалярний добуток векторів 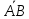 і і 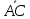
A.-14
B.4
C.6
D.5
|
В
|
ХХ..01.03.А.ПА.02
|
2
|
ХХ..01.03
|
Задано точки А(1,-3,1), В(-1,-2,3), С(2,3,4). Знайти скалярний добуток векторів 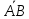 і і 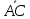
A.13
B.4
C.11
D.10
|
D
|
ХХ..01.03.А.ПА.03
|
2
|
ХХ..01.03
|
Задано точки А(-1,1,3), В(1,-2,2), С(1,4,2). Знайти скалярний добуток векторів 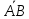 і і 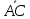
A.4
B.-4
C.10
D.-10
|
В
|
ХХ..01.03.А.ПА.04
|
2
|
ХХ..01.03
|
Задано точки А(-5,-3,-4), В(1,4,6), С(3,2,-2). Знайти скалярний добуток векторів 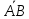 і і 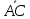
A.103
B.97
C.25
D.108
|
А
|
ХХ..01.03.А.ПА.05
|
2
|
ХХ..01.04
|
Векторним добутком векторів називається:
число, що дорівнює 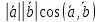
вектор, що задовольняє умовам:
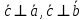
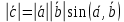
Вектори утворюють праву трійку.
вектор, що задовольняє умовам:
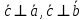
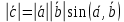
Вектори утворюють ліву трійку.
вектор, що задовольняє умовам:
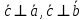
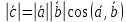
Вектори утворюють праву трійку.
|
B
|
ХХ..01.04.А.ПА.01
|
2
|
ХХ..01.04
|
Скалярним добутком векторів називається:
число, що дорівнює 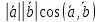
вектор 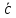 , що , що 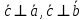
число, що дорівнює 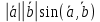
нульовий вектор.
|
A
|
ХХ..01.04.А.ПА.02
|
2
|
ХХ..01.04
|
Два вектори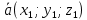 і і 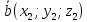 взаємно перпендикулярні, якщо: взаємно перпендикулярні, якщо:
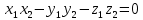
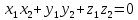
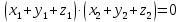
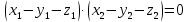
|
B
|
ХХ..01.04.А.ПА.03
|
2
|
ХХ..01.04
|
Два вектори колінеарні, якщо:
A.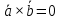
B.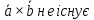
C.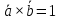
D. інша відповідь.
|
|
ХХ..01.04.А.ПА.04
|
2
|
ХХ..01.04
|
Скалярний добуток векторів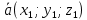 і і 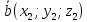 можна обчислити за формулою: можна обчислити за формулою:
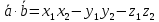
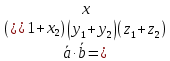
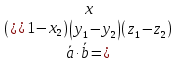
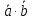 = = 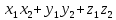
|
D
|
ХХ..01.04.А.ПА.05
|
2
|
ХХ..01.05 Елементи аналітичної геометрії на площині і в просторі.
|
Дано координати точок А(-2,4) і В(3,1). Скласти рівняння прямої АВ.
A.3x-5y+11=0
B.5x-3y+12=0
C.3x+5y-14=0
D.5x+3y+14=0
|
C
|
ХХ..01.05.А.ПА.01
|
2
|
ХХ..01.05
|
Дано координати точок А(1,4) і В(-2,1). Скласти рівняння прямої АВ.
A. x-y+3=0
B. x+y-3=0
C. –x+y-5=0
D. x+y+5=0
|
A
|
ХХ..01.05.А.ПА.02
|
2
|
ХХ..01.05
|
Дано координати точок А(2,4) і В(-3,-1). Скласти рівняння прямої АВ.
A. x-y+5=0
B.y-x+5=0
C.y-x+2=0
D. x-y+2=0
|
D
|
ХХ..01.05.А.ПА.03
|
2
|
ХХ..01.05
|
Дано координати точок А(1,-1) і В(3,5). Скласти рівняння прямої АВ.
A.3x-y+6=0
B. x-3y+5=0
C.3x-y-4=0
D. x-3y+2=0
|
C
|
ХХ..01.05.А.ПА.04
|
2
|
ХХ..01.05
|
Дано координати точок А(-4,1) і В(2,6). Скласти рівняння прямої АВ.
A. 5x-6y+6=0
B. 5x-6y+26=0
C. 5x+6y+2=0
D. 5x+6y+16=0
|
B
|
ХХ..01.05.А.ПА.05
|
2
|
Диференціальне числення функції однієї змінної. Похідна функції. Диференціал функції однієї змінної. Основні теореми диференціального числення.
ХХ..01.07
|
Рівняння дотичної до графіка функції 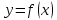 в точці в точці 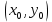 має вид: має вид:
A.
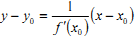
B.
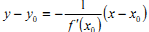
C. 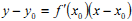
D. 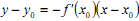
|
C
|
ХХ..01.07.А.ПА.01
|
2
|
ХХ..01.07
|
Рівняння нормалі до графіка функції 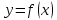 в точці в точці 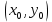 має вид: має вид:
A.
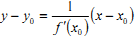
B.
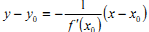
C. 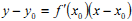
D. 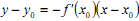
|
B
|
ХХ..01.07.А.ПА.02
|
2
|
ХХ..01.07
|
Які з наступних рівностей є правильними?
1.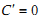
2.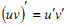
3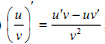
4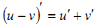
1 i 3
2 i 4
1 i 4
3 i 4
|
A
|
ХХ..01.07.А.ПА.03
|
2
|
ХХ..01.07
|
Які з наступних рівностей є правильними?
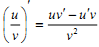
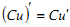
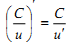
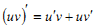
1, 2, 4.
2, 3, 4.
1, 2, 3.
1, 3, 4.
|
A
|
ХХ..01.07.А.ПА.04
|
2
|
ХХ..01.07
|
Які з наступних рівностей є правильними?
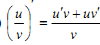
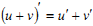
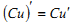
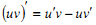
2,4.
3, 4.
2, 3.
1, 4.
|
C
|
ХХ..01.07.А.ПА.05
|
2
|
Функції двох змінних. ХХ..01.10
|
Функція двох змінних має у точці 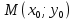 екстремум, якщо виконується умова: екстремум, якщо виконується умова:
A. A. 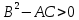
B.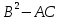 =0 =0
C.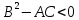
D.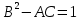
|
C
|
ХХ..01.10.А.ПА.01
|
2
|
ХХ..01.10
|
Функція двох змінних має у точці 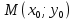 максимум якщо виконується умова: максимум якщо виконується умова:
A. 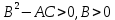
B.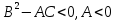
C.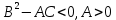
D.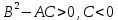
|
B
|
ХХ..01.10.А.ПА.02
|
2
|
ХХ..01.10
|
Функція двох змінних має у точці 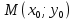 мінімум, якщо виконується умова: мінімум, якщо виконується умова:
A. 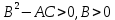
B.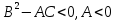
C.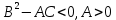
D.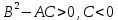 . .
|
C
|
ХХ..01.10.А.ПА.03
|
2
|
ХХ..01.10
|
Функція двох змінних має у точці 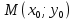 максимум, якщо виконується умова: максимум, якщо виконується умова:
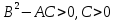
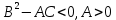
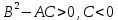 . .
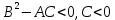
|
D
|
ХХ..01.10.А.ПА.04
|
2
|
ХХ..01.10
|
Функція двох змінних має у точці 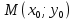 не має екстремуму, якщо виконується умова: не має екстремуму, якщо виконується умова:
A. 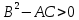
B.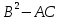 =0 =0
C.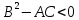
D.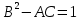
|
A
|
ХХ..01.10.А.ПА.05
|
2
|
Визначений інтеграл. Його властивості
ХХ..02.03
|
Якщо поміняти місцями межі інтегрування у визначеному інтегралі, то:
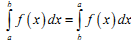
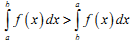
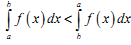
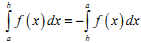
|
B
|
ХХ..02.03.А.ПА.01
|
|
ХХ..02.03
|
Для будь-яких чисел a, b, c має місце рівність:
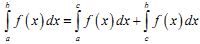
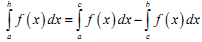
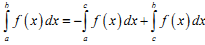
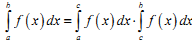
|
A
|
ХХ..02.03.А.ПА.02
|
2
|
ХХ..02.03
|
Формула Ньютона-Лейбніца має вид:
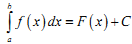
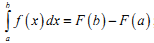
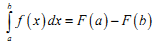
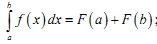
|
B
|
ХХ..02.03.А.ПА.03
|
2
|
ХХ..02.03
|
Якщо m M - відповідно найменше і найбільше значення функції y=f(x) на відрізку [ a,b]; , то:
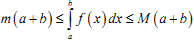
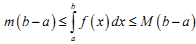
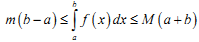
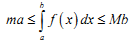
|
B
|
ХХ..02.03.А.ПА.04
|
2
|
ХХ..02.03
|
Теорема про середнє. Якщо функція y=f(x) неперервна на відрізку [ a,b], то знайдеться точка c∈[ a,b] така, що:
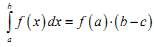
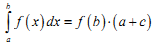
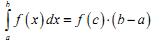
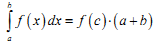
|
C
|
ХХ..02.03.А.ПА.05
|
2
|
ХХ..02.05
|
Порядком диференціального рівняння називається:
найвищий степінь невідомої функції
найвищий порядок похідної невідомої функції
найвищий степінь вільної змінної
інша відповідь
|
B
|
ХХ..02.05.А.ПА.01
|
2
|
ХХ..02.05
|
Яке з наведених нижче рівнянь є рівнянням з відокремлюваними змінними ?
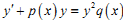
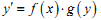
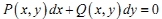
інша відповідь
|
В
|
ХХ..02.05.А.ПА.02
|
2
|
ХХ..02.05
|
Рівняння y`=f(x,y) є однорідним, якщо функція y=f(x,y) задовольняє умові:
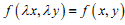
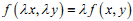
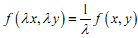
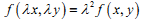
|
A
|
ХХ..02.05.А.ПА.03
|
2
|
ХХ..02.05
|
Вставити пропущений термін. Рівняння виду 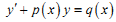 називається рівнянням ________. називається рівнянням ________.
Бернуллі
Однорідним
Лінійним
в повних диференціалах
|
C
|
ХХ..02.05.А.ПА.04
|
2
|
ХХ..02.05
|
Яка із замін використовується при розв’язуванні лінійного диференціального рівняння першого порядку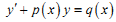 ? ?
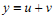
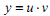
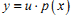
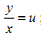
|
B
|
ХХ..02.05.А.ПА.05
|
2
|
Диференціальні рівняння ІІ порядку. Диференціальні рівняння ІІ порядку, що допускають зниження порядку.
ХХ..02.06
|
Якщо характеристичне рівняння ЛОДР ІІ порядку 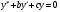 має два однакові корені має два однакові корені 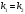 , то його загальний розв'язок має вигляд: , то його загальний розв'язок має вигляд:
А. 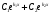
B. 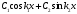
С. 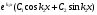
D. 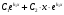
|
D
|
ХХ..02.06.А.ПА.01
|
2
|
ХХ..02.06
|
ЛОДР ІІ порядку з постійними коефіцієнтами 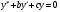 має характеристичне рівняння виду: має характеристичне рівняння виду:
А. 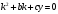
B. 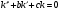
С. 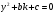
D. 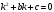
|
D
|
ХХ..02.06.А.ПА.02
|
2
|
ХХ..02.06
|
Якщо характеристичне рівняння ЛОДР ІІ порядку 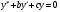 має два різні дійсні корені має два різні дійсні корені 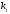 і і 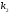 , то його загальний розв'язок має вигляд: , то його загальний розв'язок має вигляд:
А. 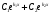
B. 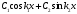
С. 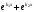
D. 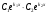
|
A
|
ХХ..02.06.А.ПА.03
|
2
|
ХХ..02.06
|
Якщо характеристичне рівняння ЛОДР ІІ порядку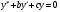 має комплексні корені має комплексні корені 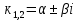 , то його загальний розв'язок має вигляд: , то його загальний розв'язок має вигляд:
А. 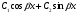
B. 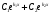
С. 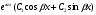
D. Інша відповідь
|
С
|
ХХ..02.06.А. ПА.04
|
2
|
ХХ..02.06
|
Які корені має характеристичне рівняння ЛОДР ІІ порядку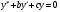 , якщо його загальний розв'язок має вигляд , якщо його загальний розв'язок має вигляд 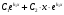
А. дійсні корені 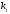 ≠ ≠ 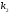 , ,
B. дійсні корені 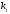 = = 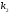 , ,
С. комплексні корені
D. інша відповідь
|
В
|
ХХ..02.06.А.ПА.05
|
2
|
 Скачать 222.33 Kb.
Скачать 222.33 Kb.
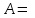
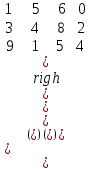 і
і 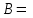
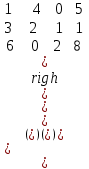 .
.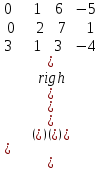
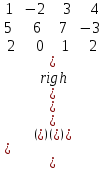
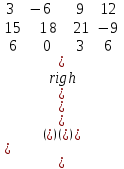
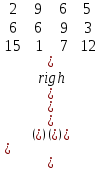 .
.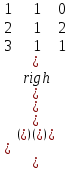 ;
;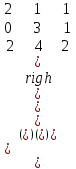 ;
; 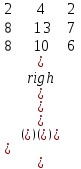
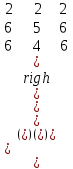
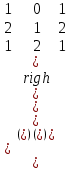
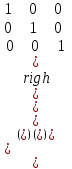
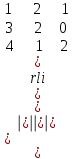 .
.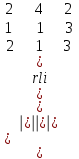 .
. 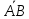 і
і 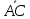
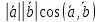
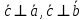
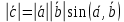
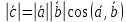
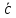 , що
, що 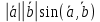
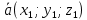 і
і 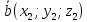 взаємно перпендикулярні, якщо:
взаємно перпендикулярні, якщо: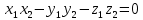
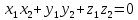
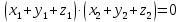
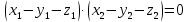
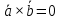
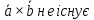
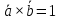
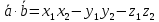
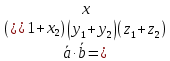
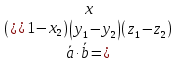
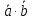 =
= 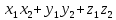
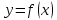 в точці
в точці 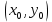 має вид:
має вид: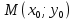 екстремум, якщо виконується умова:
екстремум, якщо виконується умова: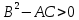
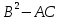 =0
=0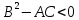
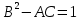
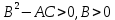
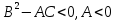
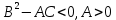
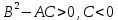
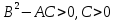
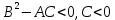
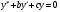 має два однакові корені
має два однакові корені 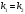 , то його загальний розв'язок має вигляд:
, то його загальний розв'язок має вигляд: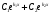
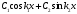
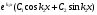
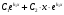
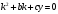
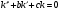
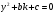
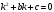
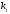 і
і 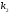 , то його загальний розв'язок має вигляд:
, то його загальний розв'язок має вигляд: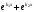
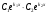
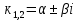 , то його загальний розв'язок має вигляд:
, то його загальний розв'язок має вигляд: