20 билет на ТАУ. 20 билет. Протокол 6 от 19 мая 2021 года Модель системы в виде дифференциального уравнения
 Скачать 78.17 Kb.
|
1. Дифференциальные уравнения являются наиболее эффективным инструментом при моделировании динамических систем. Модели в виде дифференциальных уравнений находят применение в системах автоматического управления (станки с ЧПУ, самонаводящиеся системы, электронные схемы, блоки управления оборудованием и прочее), а также применяют при моделировании социальных и биологических процессов. Математические модели элементов и системы в целом в теории автоматизированного управления (ТАУ) часто представляют обыкновенными дифференциальными уравнениями записанными в операторной (символической) форме, основанное на использовании условного (символического) обозначения производных и интеграла:  , где  =1,2,3…;  .При записи дифференциальных уравнений в операторной форме оператор  следует рассматривать как алгебраический сомножитель, а выражение  – как произведение, не обладающее свойством коммутативности: нельзя вместо рy писать  .Дифференциальные уравнения в ТАУ обычно приводят к стандартной форме, для чего делят все члены уравнения на коэффициент слагаемого при выходной координате, не содержащего оператор. Если коэффициент равен нулю, деление выполняют на первый, отличный от нуля, коэффициент при самой младшей производной от выходной координаты. При записи линейных уравнений в ТАУ принято выходную величину и ее производные записывать в левой части уравнения, а все остальные члены переносить в правую часть. Все перечисленные правила делают запись дифференциальных уравнений более компактной и удобной для практического применения. Пусть объект описывается следующим уравнением  .Вводя оператор (символ) дифференцирования  , получим: ,или в более компактной форме  .Запишем последнее уравнение в стандартной форме:  .Широко пользуются следующими обозначениями:    .Коэффициенты  и  имеют размерность времени и называются постоянными времени. Коэффициент передачи  характеризует передаточное отношение элемента (системы) в установившемся режиме. Размерность определяется размерностями переменных  и  .С учетом принятых обозначений исходное дифференциальное уравнение приводим к стандартной форме:  Решить уравнение, т.е. найти реакцию элемента  на изменение  , можно, если задан закон изменения  и определены начальные условия ;  ;  .В ТАУ широко пользуются нулевыми начальными условиями, полагая:    .В более общем случае модель вида «вход–выход» описывается скалярным обыкновенным линейным дифференциальным уравнением  –порядка с постоянными коэффициентами, которые, используя операторные полиномы  и  или А(р) и В(р), можно записать в компактной форме , (1)где  – собственный оператор; – оператор воздействия.Передаточная функция – это способ математического описания динамической системы. Передаточная функция линейной системы определяется как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной при условии, что все начальные условия равны нулю. Преобразование Лапласа – это интегральное преобразование, которое связывает между собой функцию комплексного переменного с функцией вещественного переменного. Передаточная функция системы (или элемента) однозначно описывает динамическую связь между этими переменными. Передаточная функция существует только для линейных стационарных (с постоянными параметрами) систем. В нестационарных системах один или несколько параметров зависят от времени, поэтому преобразованием Лапласа воспользоваться нельзя. Передаточная функция описывает поведение системы в терминах вход-выход и не несет никакой информации о внутренних переменных и характере их изменения. Уравнение (1) часто представляют в следующем виде  . (2)Отношение оператора воздействия к собственному оператору звена называют операторной передаточной функцией W(p), которую записывают не производя возможных сокращений. Запись (2) является чисто символической и не дает решения уравнения (1). Для рассматриваемого примера:  .Передаточная функция не зависит от закона изменения внешнего воздействия и определяется только свойствами элемента относительно выбранного воздействия. При одной выходной координате число  , характеризующих динамику элемента, определяется числом входных переменных.Более строгое определение передаточной функции как наиболее компактной формы описания динамических свойств элементов и систем основано на применении преобразования Лапласа. При этом считается, что рассматриваемой функции времени , которую называют оригиналом, можно найти «лапласово изображение»  : ,где  – комплексная переменная.Преобразование Лапласа возможно, если:  при  ; при  растет не быстрее некоторой показательной функции  , где  и   постоянные; на любом конечном отрезке времени однозначна, конечна и кусочно–непрерывна.Составлены таблицы (примеры даны в табл.1), позволяющие определять изображение по оригиналу и выполнять обратное преобразование Лапласа, т.е. находить оригинал по изображению. В основе этого способа перехода от дифференциальных уравнений к передаточным функциям лежат следующие правила:  ;  ,справедливые при нулевых начальных условиях. Здесь  – символ интеграла Лапласа (читается Лапласиан). Обратное преобразование Лапласа, позволяющее найти оригинал по изображению, обозначают  .Применим приведенные правила к дифференциальному уравнению второго порядка  ,получим алгебраическое уравнение  ,где – комплексная переменная.Отношение изображения по Лапласу выходной величины к изображению входной величины при нулевых начальных условиях называют передаточной функцией  .Совпадение по форме выражений для передаточных функций, полученных с использованием операционного исчисления (преобразования Лапласа) и символической (операторной) записи дифференциального уравнения, позволяет определять по дифференциальному уравнению без преобразования его по Лапласу. Следует подчеркнуть, что сходство между этими чисто внешнее и имеет место лишь для стационарных систем, т.е. для случая, когда коэффициенты уравнения постоянны.Таблица 1 Изображение простейших функций времени по Лапласу
2. Передаточную функцию формально можно получить из линейного дифференциального уравнения при нулевых начальных условиях, путем замены в нем символа дифференцирования оператором и деления образующегося при этом коэффициента или многочлена правой части (оператора воздействия) уравнения на многочлен левой части (собственный оператор). При таком переходе следует избегать сокращения общих делителей полиномов числителей и знаменателей (диполей рациональных функций). Такое сокращение приводит к потере составляющих свободных движений, вызванных ненулевыми предначальными условиями. Оператор W(p), связывающий вход звена с выходом, характеризуется структурой и параметрами. Параметрами оператора являются коэффициенты полиномов А(р) и В(р), а структура определяется заданием степеней n и m (1), где n – определяет порядок дифференциального уравнения. Наряду с полиноминальной формой (2) передаточная функция может быть задана в факторизованном виде  , (3)где  – множество нулей, т.е. корней уравнения В(р)=0; – множество полюсов, т.е. корней уравнения А(р)=0.Передаточные функции, все нули и полюсы которых находятся в левой полуплоскости, называют минимально-фазовыми. 3. Примеры передаточных функций различных элементов. Элемент системы, обладающий определенными свойствами в динамическом отношении, называется ее Звеном. Звенья систем регулирования могут иметь разную физическую природу (электрические, пневматические, механические и др. звенья), но описываться одинаковыми ДУ, а соотношение входных и выходных сигналов в звеньях описываться одинаковыми передаточными функциями. В ТАУ выделяют группу простейших звеньев, которые принято называть типовыми. Статические и динамические характеристики типовых звеньев изучены достаточно полно. Типовые звенья широко используются при определении динамических характеристик объектов управления. Например, зная переходную характеристику, построенную с помощью самопишущего прибора, часто можно определить, к какому типу звеньев относится объект управления, а следовательно, его передаточную функцию, дифференциальное уравнение и т.д., т.е. модель объекта. Типовые звенья Любое сложное звено может быть представлено как соединение простейших звеньев. К простейшим типовым звеньям относятся: · усилительное, · инерционное (апериодическое 1-го порядка), · интегрирующие (реальное и идеальное), · дифференцирующие (реальное и идеальное), · апериодическое 2-го порядка, · колебательное, · запаздывающее. Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета системы автоматического регулирования (САР) сводится к определению ее передаточной функции. При расчете настроек регуляторов широко используются достаточно простые динамические модели промышленных обьектов управления. В частности, использование моделей инерционных звеньев первого или второго порядка с запаздыванием для расчета настроек регуляторов обеспечивает в большинстве случаев качественную работу реальной системы управления. В зависимости от вида переходной характеристики (кривой разгона) задаются чаще всего одним из трех видов передаточной функции обьекта управления: В виде передаточной функции инерционного звена первого порядка: 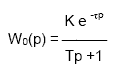 где: К - коэффициент усиления, Т - постоянная времени,  - запаздывание,которые должны быть определены в окрестности номинального режима работы обьекта.Для обьекта управления без самовыравнивания передаточная функция имеет вид: 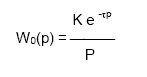 Более точнее динамику обьекта описывает модель второго порядка с запаздыванием:  | |||||||||||||||||||||||||||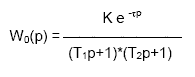
