Занятие 7. Практическое занятие 7 (1). Проверка статистических гипотез. Критерий Фишера. Непараметрические критерии Статистическая проверка гипотез
 Скачать 170.31 Kb. Скачать 170.31 Kb.
|
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7 Тема: Проверка статистических гипотез. Критерий Фишера. Непараметрические критерии Статистическая проверка гипотез. Проверка гипотез для дисперсий. Критерий Фишера. Непараметрические критерии. Критерий знаков. Статистическая проверка гипотез Терминология Статистические методы используют для описания данных и для оценки статистической значимости результатов опыта. Ни одно исследование не обходится без сравнений. Сравнивают данные опыта с контролем и т.п. Методы оценки статистической значимости различий называют критериями. Критерий – это и сам метод и та величина, которая получается в результате его применения. Методов существует множество, но все они построены по одному принципу. Итак, обратимся ко второму направлению математической статистики—проверке статистических гипотез. Статистическая гипотеза – это любое предположение о виде неизвестного распределения или о параметрах известных распределений. Статистическая гипотеза - это всякое высказывание о генеральной совокупности, проверяемое по выборке. Гипотезы будем обозначать буквой H с индексами. Будем предполагать, что у нас имеется 2 непересекающиеся гипотезы 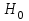 и и 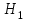 . . 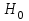 – нулевая гипотеза (или основная). – нулевая гипотеза (или основная). 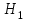 - альтернативная или конкурирующая гипотеза. - альтернативная или конкурирующая гипотеза.Сначала формулируют нулевую гипотезу, то есть предполагают, что исследуемые факторы не оказывают никакого влияния на исследуемую величину и полученные различия случайны. Нулевая гипотеза (H0) всегда отвергает эффект. Например, разность средних равна нулю. Нулевая гипотеза формулируется всегда относительно генеральной совокупности (популяции) – она более интересна, чем выборка. Затем формулируют альтернативную гипотезу (H1), которая принимается, если нулевая гипотеза неверна. Она относится к той теории, которую собираются исследовать. Проверка гипотез – это определение аргументов против гипотезы. Задача проверки статистических гипотез состоит в том, чтоб на основе выборки 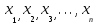 принять (т.е. считать справедливой) либо нулевую гипотезу принять (т.е. считать справедливой) либо нулевую гипотезу 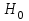 , либо конкурирующую гипотезу , либо конкурирующую гипотезу 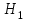 . .Для проверки принятой гипотезы используют статистический критерий – это правило, позволяющее, основываясь только на выборке 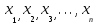 , принять либо отвергнуть нулевую гипотезу , принять либо отвергнуть нулевую гипотезу 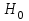 . Величина рассчитываемого критерия количественно отражает аргументы в наборе данных против нулевой гипотезы. Обычно чем больше по модулю значение критерия, тем сильнее эти аргументы. . Величина рассчитываемого критерия количественно отражает аргументы в наборе данных против нулевой гипотезы. Обычно чем больше по модулю значение критерия, тем сильнее эти аргументы.Значение критерия, полученное из выборки, связывают с уже известным распределением (теоретическим или табличным), которому оно подчиняется, чтобы определить достигнутый уровень значимости (). Значение - это максимально приемлемая вероятность, отвергающая нулевую гипотезу, если она верна, и тогда можно сказать, что результаты значимы на 5% уровне. Чем меньше значение , тем сильнее аргументы против нулевой гипотезы. Обычно полагают, что 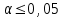 . Это значит, что аргументов достаточно, чтобы отвергнуть нулевую гипотезу, хотя есть небольшой шанс, что она справедлива (рис. 7.1). Значение - это площадь обоих ″хвостов на графике распределения вероятностей. . Это значит, что аргументов достаточно, чтобы отвергнуть нулевую гипотезу, хотя есть небольшой шанс, что она справедлива (рис. 7.1). Значение - это площадь обоих ″хвостов на графике распределения вероятностей. Рис.7.1. Достигнутый уровень значимости 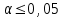 Когда отвергают нулевую гипотезу, то говорят, что результаты эксперимента статистически значимы на уровне 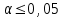 (5%). (5%).Если 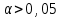 , то аргументов недостаточно, чтобы отвергнуть Н0. В этом случае говорят, что результаты статистически незначимы на уровне , то аргументов недостаточно, чтобы отвергнуть Н0. В этом случае говорят, что результаты статистически незначимы на уровне 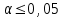 . Это не означает, что нулевая гипотеза истинна. Просто недостаточно аргументов, чтобы ее отвергнуть. . Это не означает, что нулевая гипотеза истинна. Просто недостаточно аргументов, чтобы ее отвергнуть.Различают два вида критериев: параметрические и непараметрические. Параметрические критерии представляют собой функции параметров данной совокупности и используются, если совокупности, из которых взяты выборки, подчиняются нормальному закону распределения. Часто данные не подчиняются предположениям, которые лежат в основе этих методов. В этом случае можно использовать непараметрические критерии. Непараметрические критерии применяются, если нет подчинения распределения нормальному закону. Эти критерии обычно заменяют данные выборок знаками (плюс или минус) рангами (т.е. числами 1; 2; 3; …, описывающими их положение в упорядоченном наборе данных), категориями и т.п. Непараметрический критерий можно использовать, если объем выборки небольшой настолько, что невозможно оценить закон распределения данных. Но непараметрические критерии обладают меньшей мощностью в обнаружении реального эффекта, чем аналогичный параметрический критерий. Общая постановка задачи проверки гипотез 1. Формулируют (выдвигают) нулевую гипотезу 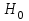 об отсутствии различий между группами, об отсутствии существенно отличия фактического распределения от некоторого заданного, например, нормального, экспоненциального и др. об отсутствии различий между группами, об отсутствии существенно отличия фактического распределения от некоторого заданного, например, нормального, экспоненциального и др.Сущность нулевой гипотезы 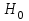 : разница между сравниваемыми генеральными параметрами равна нулю, и различия, наблюдаемые между выборочными характеристиками, носят случайный характер, т.е. эти выборки принадлежат одной генеральной совокупности. : разница между сравниваемыми генеральными параметрами равна нулю, и различия, наблюдаемые между выборочными характеристиками, носят случайный характер, т.е. эти выборки принадлежат одной генеральной совокупности.2. Формулируют альтернативную гипотезу 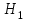 . .Задают уровень значимости 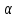 . Уровень значимости . Уровень значимости 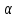 - это вероятность ошибки отвергнуть нулевую гипотезу Н0, если на самом деле эта гипотеза верна. При - это вероятность ошибки отвергнуть нулевую гипотезу Н0, если на самом деле эта гипотеза верна. При 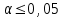 ошибка возможна в 5% случаев. ошибка возможна в 5% случаев.Для проверки нулевой гипотезы используют критерии. Критерий – это случайная величина 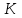 , которая служит для проверки Н0. Эти функции распределения известны и табулированы. Критерий зависит от двух параметров: от числа степеней свободы и от уровня значимости a. , которая служит для проверки Н0. Эти функции распределения известны и табулированы. Критерий зависит от двух параметров: от числа степеней свободы и от уровня значимости a.Фактическую величину критерия получают по данным наблюдения 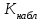 . .5. По таблице определяют критическое значение, превышение которого при справедливости гипотезы маловероятно 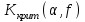 . .6. Сравнивают 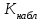 и и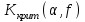 . .Если 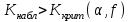 , то отвергают , то отвергают 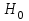 и принимают и принимают 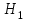 . .Если 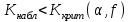 , то принимают , то принимают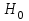 . .Это для параметрических критериев. Если использованы непараметрические критерии, то наоборот: если 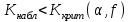 , то принимают , то принимают 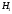 . .Вывод: различие статистически значимо  или незначимо. или незначимо.Проверка гипотез для дисперсий Пусть генеральные совокупности 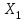 и и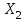 распределены нормально. По независимым выборкам объемов распределены нормально. По независимым выборкам объемов 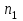 и и 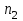 , извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии , извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии 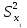 и и 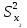 . Требуется сравнить эти дисперсии. При заданном уровне значимости . Требуется сравнить эти дисперсии. При заданном уровне значимости 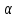 , надо проверить нулевую гипотезу о равенстве генеральных дисперсий нормальных совокупностей. , надо проверить нулевую гипотезу о равенстве генеральных дисперсий нормальных совокупностей.1. 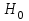 : : 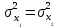 . .2. Н1 : 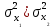 . .В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий используем случайную величину F, равную отношению большей исправленной выборочной дисперсии к меньшей 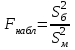 . .4. Величина F, при условии справедливости нулевой гипотезы, имеет распределения Фишера-Снедекора со степенями свободы 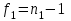 и и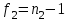 , где , где 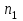 – объем выборки, по которой вычислена большая выборочная дисперсия, – объем выборки, по которой вычислена большая выборочная дисперсия, 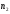 – объем выборки, по которой вычислена меньшая выборочная дисперсия. – объем выборки, по которой вычислена меньшая выборочная дисперсия.Из таблиц находим 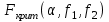 . .5. Сравниваем 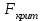 и и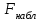 : :Если 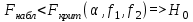 , генеральные дисперсии различаются незначимо. , генеральные дисперсии различаются незначимо.Пример 7.2. По двум независимым выборкам объемов 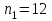 и и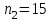 , извлеченным из нормальных генеральных совокупностей , извлеченным из нормальных генеральных совокупностей 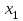 и и 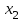 найдены исправленные выборочные дисперсии найдены исправленные выборочные дисперсии 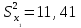 и и 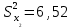 . При уровне значимости . При уровне значимости 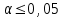 проверить нулевую гипотезу о равенстве генеральных дисперсий проверить нулевую гипотезу о равенстве генеральных дисперсий 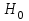 : : 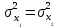 . .Решение. Конкурирующая гипотеза: 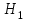 : : 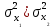 ; ;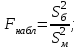 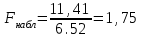 ; ;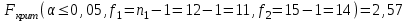 ; ;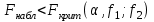 => =>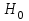 – нет оснований отвергать нулевую гипотезу о равенстве генеральных дисперсий. Значит, можно применять и критерий Стьюдента для сравнения средних. – нет оснований отвергать нулевую гипотезу о равенстве генеральных дисперсий. Значит, можно применять и критерий Стьюдента для сравнения средних.Пример 7.3. По двум независимым малым выборкам объемов 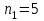 и и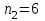 , извлеченным из нормальных генеральных совокупностей , извлеченным из нормальных генеральных совокупностей 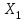 и и 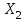 , найдены выборочные средние , найдены выборочные средние 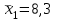 и и 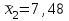 и выборочные дисперсии и выборочные дисперсии 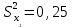 и и 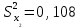 . При уровне значимости . При уровне значимости 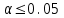 проверить нулевую гипотезу проверить нулевую гипотезу 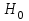 : :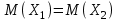 . .Решение. Так как выборочные дисперсии различны, проверим предварительно нулевую гипотезу о равенстве генеральных дисперсий, пользуясь критерием Фишера-Снедекора. Найдем отношение большей исправленной дисперсии к меньшей: 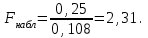 По таблице при 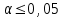 и числам степеней свободы и числам степеней свободы 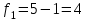 и и 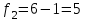 , находим критическую точку , находим критическую точку 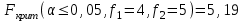 . .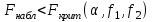 => =>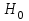 – нет оснований отвергать нулевую гипотезу о равенстве генеральных дисперсий. Теперь можно сравнить средние. – нет оснований отвергать нулевую гипотезу о равенстве генеральных дисперсий. Теперь можно сравнить средние.Вычислим наблюдаемое значение критерия Стъюдента: 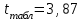 . .По таблице находим критическую точку: 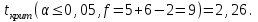 Так как 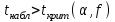 => =>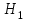 – выборочные средние различаются значимо. – выборочные средние различаются значимо.Непараметрические критерии Это функции, зависящие непосредственно от вариант данной совокупности с их частотами. Служат для проверки рабочих гипотез независимо от формы распределения совокупностей, из которых взяты сравниваемые выборки. Непараметрические критерии рассматривают не только количественные, но и качественные признаки, многие из которых выражаются порядковыми номерами, рангами, индексами и пр. Например, критерий знаков, критерий Уилкоксона-Манна-Уитни. Критерий знаков Рассмотрим критерий знаков. Требования: 1) законы распределения X и Y предполагаются неизвестными, но одинаковыми; 2) объем выборок 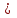 100 и больше и одинаков. 100 и больше и одинаков.Критерий знаков применяют для проверки нулевой гипотезы 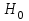 : совокупности, из которых взяты сравниваемые выборки, имеют одну и ту же или одинаковые функции распределения : совокупности, из которых взяты сравниваемые выборки, имеют одну и ту же или одинаковые функции распределенияВводится величина 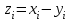 . Значения этой разности меняются от опыта к опыту по величине и знаку. Если влияние фактора незначимо, то вероятно появление как положительных . Значения этой разности меняются от опыта к опыту по величине и знаку. Если влияние фактора незначимо, то вероятно появление как положительных 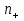 , так и отрицательных , так и отрицательных 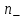 . Из этих величин выбирают наименьшее . Из этих величин выбирают наименьшее 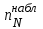 , которое станет наблюдаемым значением критерия. , которое станет наблюдаемым значением критерия.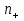 и и 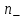 => =>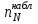 (min) – это наименьшее число из однозначных разностей. (min) – это наименьшее число из однозначных разностей.Значение 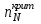 находят по формуле или из таблиц. Если по формуле, то это целая часть числа А. находят по формуле или из таблиц. Если по формуле, то это целая часть числа А.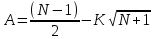 , где , гдеN – объем выборки. К = 0,98 при 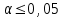 . .Сравниваем. Если 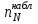 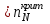 => =>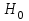 , то принимается нулевая гипотеза. Различие недостоверно. Действие фактора незначимо. , то принимается нулевая гипотеза. Различие недостоверно. Действие фактора незначимо.Пример 7.5. Проведено 100 опытов по изучению влияния фактора на артериальное давление. При 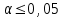 оценить значимость различия в действии данного фактора на группы животных, если положительная разность давлений оценить значимость различия в действии данного фактора на группы животных, если положительная разность давлений 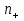 наблюдалась 48 раз, а отрицательная n – 44 раза. наблюдалась 48 раз, а отрицательная n – 44 раза.Решение. Из чисел 48 и 44 выбираем наименьшее – это 44: 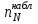 = 44. = 44.Найдем 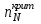 по формуле: по формуле: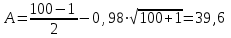 . .Целая часть числа – 39: 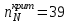 . .44 > 39, 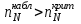 => =>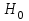 . .Принимаем 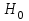 . Влияние фактора незначимо. . Влияние фактора незначимо. |
