Проверочная работа. Задания дифференцированы по вариантам (вариант 1 более простой уровень)
 Скачать 17.97 Kb. Скачать 17.97 Kb.
|
|
Проверочная работа. Задания дифференцированы по вариантам (вариант 1- более простой уровень). Вариант 1
а) f (х) = 3 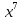 + 4 + 4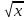 ; б) f (х) = ; б) f (х) = 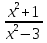 . .2. Вычислите производную функции f (х) = 2 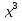 + + 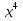 в точках 2; 3. в точках 2; 3.3. Решите неравенство f ′ (х) ≤ 0, если f (х) = 4х + 2 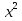 . .Вариант 2 1.Найдите производную функции: а) f (х) = 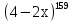 ; б) g (х) = ; б) g (х) = 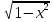 . .2. Решите уравнение f ′(х) = 0 неравенство f ′(х) > 0 для функции f (х) = 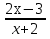 . . 3. Даны функции f (х) = 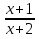 и g (х) = и g (х) = 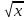 . .Задайте с помощью формул функции f (g(х)) и g (f(х)). Вариант 3 1.Найдите производную функции: а) f (х) = 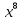 - 4 - 4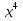 - - 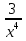 + 3 ; б) f (х) = + 3 ; б) f (х) = 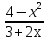 . .2. Вычислите производную функции f (х) = (х + 1) 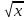 в точках 2; 3. в точках 2; 3.3.Дана функция f (х) = х + 4. Найдите такую функцию g, чтобы выполнялось равенство f(g(х)) = х. Вариант 4 1.Найдите производную функции: а) f (х) = 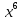 - 2 - 2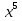 + + 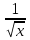 - 3 ; б) g (х) = (х + 5) - 3 ; б) g (х) = (х + 5)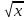 . .2.Вычислите производную функции f(х) = 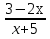 в точках -3, в точках -3, 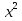 - 5. - 5.3.Решите неравенство f ′ (х) ≥ 0, если f(х) = х + 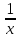 . .Вариант 5 1.Найдите производную функции у = 100 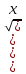 - 10 - 10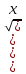 в точке 1. в точке 1.2.Решите уравнение f′ (х) = 0 и неравенство f ′(х) > 0 для функции f(х) = 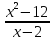 . .3.Даны функции f (х) = 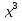 + 2х и g (х) = + 2х и g (х) =  . Задайте с помощью формул функции f(g(х)) и g(f(х)). . Задайте с помощью формул функции f(g(х)) и g(f(х)). |
