Прямоугольный треугольник (стр. 70) - это…
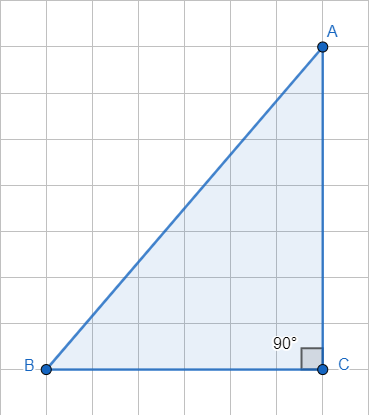
Подписать название сторон:
AB -
AC -
BC -
Записать свойство острых углов (стр. 75):
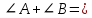 ... ...
|
|
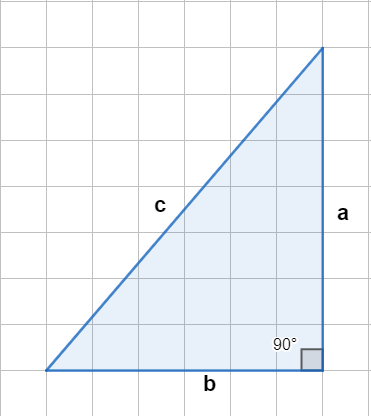
Теорема Пифагора (стр. 128):..............................
c - гипотенуза
a - ...
b - ...
Записать формулы:
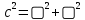
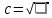
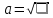
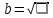
|
|
Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.
Например, прямоугольный треугольник со сторонами 3, 4, 5. Так как 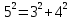 . .
|
Запишите 4 примера пифагоровых треугольников:
1)..............................................................
2)..............................................................
3)..............................................................
4)..............................................................
|
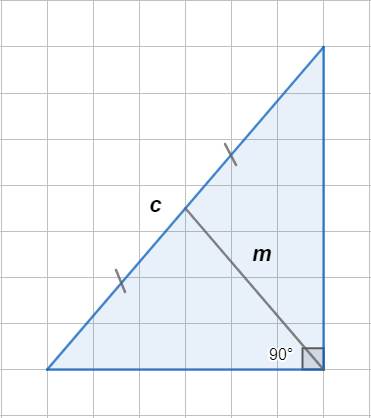
Свойство медианы, проведенной из прямого угла:....
m - медиана
c - гипотенуза
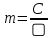
|
|
Прямоугольный равнобедренный треугольник - это…
…………………………………………………………………
|
Сделать чертёж, обозначить равные углы, равные стороны.
|
Свойство катета, лежащего против угла в 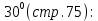 ………………………………………………………………... ………………………………………………………………...
………………………………………………………………...
AB обозначим как c
BC обозначим как a
AC обозначим как b
Записать обозначения для сторон прямоугольного треугольника через другие стороны:
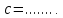
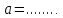
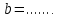
|
|
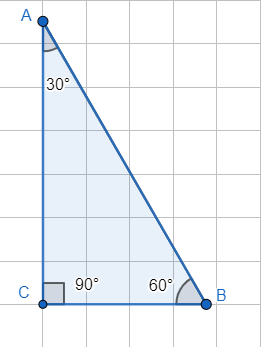
Подписать названия сторон, записать формулы (стр. 154-155):
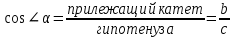

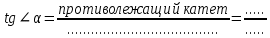

|
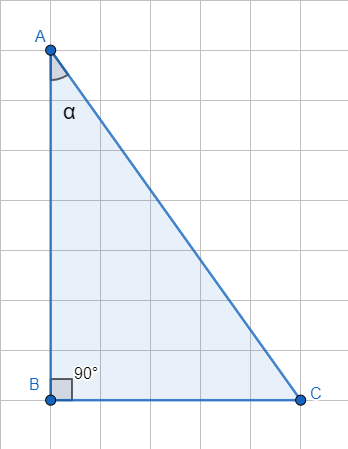
|
Выучить таблицу:
|
Заполнить пропуски:
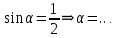
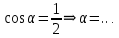
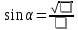
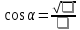
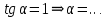
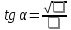
|
Основное тригонометрическое тождество (стр. 156):........
Формула тангенса (стр. 155):
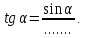
|
Из основного тригонометрического тождества выразить:
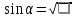
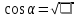
|
 Скачать 60.9 Kb.
Скачать 60.9 Kb.