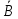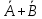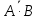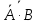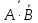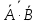Р. С. Кударов Задание для контрольной работы по дисциплине математика
 Скачать 50.48 Kb. Скачать 50.48 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего образования “петербургский государственный университет путей сообщения ИМПЕРАТОРА АЛЕКСАНДРА I” Кафедра «Высшая математика» Р.С. Кударов Задание для контрольной работы по дисциплине «МАТЕМАТИКА» (Б1.О.7) для специальности (23.05.04) «Эксплуатация железных дорог» по специализациям «Магистральный транспорт» «Грузовая и коммерческая работа» «Пассажирский комплекс железнодорожного транспорта» «Транспортный бизнес и логистика» КОНТРОЛЬНАЯ РАБОТА 7 – ВЕРОЯТНОСТИ СОБЫТИЙ И ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Санкт-Петербург 2020 (1-10) Вероятности четырех независимых в совокупности событий A1, A2, A3, A4 соответственно равны P( A1 ) 0,1; P( A2 ) 0,2; P( A3 ) 0,3 и P( A4 ) 0,4 . События B1 и B2 заданы с помощью словесного описания. Используя операции алгебры событий, выразите события B1 и B2 через A1, A2, A3, A4. Найдите вероятности событий B1 и B2.
(11–20) По вероятности P(A) и P(B) найти следующие вероятности Р(С) и Р(А|С) при условии, что А и В независимы.
(21-30) Из урны, содержащей mбелых и nчерных шаров случайным образом вынимают 4 шара. Найти вероятности следующих событий: a. шары одного цвета; b. два шара черных и два шара белых; c. три шара одного цвета, а четвертый другого цвета.
(31-40) Вероятность попадания стрелком в мишень равна P(n m). Найти вероятность того, что спортсмен поразит мишень ровно m раз в n выстрелах, если вероятность попадания при одном выстреле равна p.
(41-50) В последовательности испытаний по схеме Бернулли известна вероятность успеха P( A) p. Найти следующие вероятности P(n m) , P(n m) , P(m1 n m2 ) , где n – число успехов в последовательности из nиспытаний.
 (51-60) Дискретная случайная величина , принимающая значения xi (51-60) Дискретная случайная величина , принимающая значения xiтаблицей распределения. ( i 1,5 ), задана
Постройте функцию распределения F( x) случайной величины , найдите математи- ческое ожидание M , дисперсию D , вероятность события P( M ) .
|

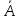 + В
+ В