Әлемді сандарсыз елестетуге бола ма. р трлі екі блгіші бар сандар жай сандар деп аталады
 Скачать 21.6 Kb. Скачать 21.6 Kb.
|
|
Әлемді сандарсыз елестетуге бола ма? Сандар түсінігінің пайда болуының өзі – адамзат ақыл-ойының жарқын жемісі. Шынымен де, сандар көмегімен өлшейді, салыстырады, есептейді, ал тағы сурет салады, сызба жасайды, ойнайды, тұжырымдайды, қорытынды жасайды. Сан — математиканың негізгі ұғымдарының бірі. Қарапайым түрде алғашқы қоғамдарда-ақ пайда болған, кейін бірте-бірте қолданыс аясы кеңейіп әрі жалпыланды. Кейбір заттарды санауға байланысты бүтін оң (натурал) сандар ұғымы, кейіннен сандардың натурал қатарының (1, 2, 3, 4, …) шексіздігі туралы идея пайда болды. Сан ұғымының алғашқы кеңеюі — натурал сандарға бөлшек сандардың қосылуы болды. Ол ұзындықты өлшеу, ауданды табу, сондай-ақ, атаулы шамалардың үлесін бөліп шығару қажеттілігіне байланысты қолданысқа енгізілді. Теріс сандар арифметикалық есептерді шешудің жалпы тәсілдерін беретін алгебраның ғылым ретінде дамуына байланысты шықты. Бүтін, бөлшек (оң және теріс) және нөл сандары рационал сан деп аталды. Айнымалы шамалардың шексіз өзгеруін зерттеу үшін сан ұғымы кеңейтіліп, нақты сандар жиынтығы пайда болды. Шамалардың қатынасын өрнектеу қажеттігі иррационал сандар ұғымын енгізуге себепші болды. ХҮІ ғасырда квадрат және куб теңдеулерді шешуге байланысты жорамал сандар ұғымы енгізілді. Пайда болу уақыты бойынша ең ежелгісі-натурал сандар. Натурал сандар нәрселерді санауда қолданады. Бастауыш сыныпта біз тақ және жұп сандармен таныстық, ал 5 сыныптың математика сабағында жай және құрама сандар пайда болады. Сонымен қатар натурал сандардың арасында кемел сандар, достас сандар, палиндромдар тағы басқа сандар түрі болады екен, бірақ біздер ол туралы мектепте оқымайды екенбіз. Ең бірінші жай сандардан бастайық. Егер жай сандарды барлық натурал сандар тұрғызылатын «кірпіштер» десек, онда оларды «қалау» арқылы таңғажайып «сандар қамалын» алуға болады. Бұл жай сандар деген соншалықты «жай ма»? Әр түрлі екі бөлгіші бар сандар жай сандар деп аталады. Мысалы, 5=1∙5, 29=1∙29, 37=1∙37 және т.б. Ең кіші жай сан – 2. Бұл жалғыз ғана жұп жай сан. Кішігірім зерттеу жүргізейік. Натурал сандарды екі жай санның көбейтіндісі күйінде қарастырайық, Мысалы: 12=2∙2∙3; 18=2∙3∙3; 140=2∙2∙5∙7 және т. б. Енді математикадағы жай сандардың ролін жеңіл түсіндіруге болады: олар көбейтудің көмегімен қалған басқа барлық сандар тұрғызылатын сол «кірпіштер» екен. Барлық жай сандарды санауға бола ма? Ертеде-ақ ежелгі грек математигі Евклид ең үлкен жай санның табылмайтынын тұжырымдаған. Барлық қалған сандарды оқып-үйренуде жай сан маңызды роль атқаратын болса, олардың тізімін жасау керек қой! Әрине, ең үлкен жай санның жоқ екенін білгеннен кейін, барлық жай санның тізімін жасауға үміттенуге болмайды. Бірақ 1000-ға дейінгі жай сандардың тізімін жасауға болатын шығар. Бұл жөнінде, яғни жалпы жай сандардың тізімін қалай жасау керектігі туралы біздің жыл санауымызға дейінгі ІІІ ғасырда өмір сүрген александриялық ғалым Эратосфен ойға қалды. Эратосфен өте жан-жақты адам болды: ол сандар теориясымен де, жұлдыздарды зерттеумен де айналысты. Бірақ оның есімі ғылымда жай сандарды іздеу әдісімен мәңгіге қалды. Ол математикамен қатар астрономия, география, тарихты да жақсы білген. Сол кездегі белгілі әлем картасы мен аспан денелерінің картасын жасаған, сондай-ақ кібісе (високосный) жылды еңгізудің қажеттілігін негіздеген. Оның негізгі жетістігі – Жердің көлемін адамдар оның шар тәріздес екенін білгенге дейін есептеп шығаруы. Эратосфен жай сандардың кестесін жасауға арналған өзінің тәсілін ұсынды. Эратосфен балауыздан жасалған тақтайшада натурал сандарды алып тастап отырған. Сонда алғашқы кесте елек тәрізденіп, онда тек қана жай сандар қалған. Сондықтан оны Эратосфен елегі деп атаған. Сонымен, бірінші жай сан – 2. Оны қалдыра отырып, екіге еселік болатын сандарды сызып тастаймыз. Келесі жай сан – 3. Оны қалдырып үшке еселік сандарды сызамыз және т.с.с. Нәтижесінде жай сандар тізбесін аламыз. Жай сандарды өте ұзақ еңбекті қажет ететін есептеулер арқылы алуға болады. Жақында 25692 цифрдан тұратын жай сан табылды! Оның жай сан екенін дәлелдеу үшін тез әрекет ететін компьютердің өзіне бірнеше апта қажет болды. Көріп отырғанымыздай, жай сандарды оңай табу мүмкін болмағандықтан, оларды құпия шифрлар үшін қолданатын болды, ал біз жай сандарды басқа таңғажайып сандарды табу үшін қолданатын боламыз. Натурал сандарды 2-ден бастап 6 бағанға орналастырамыз. Жай сандарды табу үшін сүзіп алатын Эратосфен «торының» бір моделін аламыз. Дөңгелекпен қоршалғандардың бәрі-жай сандар. Құрама сандардың үсті сызылған. 5-тен басталатын барлық жай сандар тек қана екі бағанда: 4 пен 6-шы бағанда. 4-ші және 6-шы бағандардың қайсыбір жолында екі жай сан кездессе, онда бұл жай сандар «егіз» сандар жұбы деп аталады: (5;7), (11;13), (17;19), (29;31), (41;43) және т.с.с. 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 Енді кемел сан деген қандай сан? Натурал санның бөлгіші деп берілген сан қалдықсыз бөлінетін санды айтатыны белгілі. п натурал санның өзінен басқа бөлгіштерінің қосындысы п натурал санның өзіне тең болса, онда п саны кемел сан деп аталады Қазірге дейін мынандай сұрақтардың жауабы табылмаған: 1) Ең үлкен кемел сан бар ма? 2) Тақ сандардың ішінде кемел сан бар ма? Ежелгі Грецияның математиктері алғашқы кемел сан ретінде «6» санын таныды. Тіпті шақырылған қонақта 6-орында ең құрметті қонақ отырған. 6 санының бөлгіштері 1, 2, 3 және 6-ның өзі. Егер 6-дан басқа бөлгіштерді 1 + 2 + 3 қоссақ, онда біз 6 санын аламыз. Сондықтан, 6 саны алғашқы кемел сан болып табылады. Ертеден белгілі келесі кемел сан "28". Шынымен де, 28 санының бөлгіштері 1, 2, 4, 7, 14 сандары. 1+2+4+7+14=28. Ежелгі грек математигі Евклидке дейін тек қана осы екі кемел сан белгілі болды және ешкім де басқа кемел сандардың бар екенін, тіпті қанша болуы мүмкін екенін де білмеді. Евклид тағы екі кемел санды таба алды: 496 и 8128. Бір жарым мың жылға жуық адамдар тек қана осы төрт санды білді. Кемел сандар мынандай қасиеттерге ие: - Барлық кемел сандар үшбұрышты. Бұл дегеніміз, кемел санды шарларды алсақ, олардан әрқашан да тең қабырғалы үшбұрыштарды құрастыруға болады деген сөз. - Кемел сандардың өзін қоса алғандағы бөлгіштеріне кері сандардың қосындысы әр уақытта 2-ге тең болады. 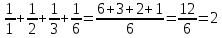  Әлемде кемел сандар сирек кездеседі. Қазіргі кезде 30-дан астам ғана кемел сан табылған. Егер бір натурал санның өзінен басқа бөлгіштерінің қосындысы екінші натурал санға тең болса немесе керісінше болса, онда мұндай екі натурал сан достас сандар деп аталады. Осы сандарға алғаш назар аударған ежелгі грек ойшылы Самостық Пифагор (б.з.б. 570 - 500) болған. Сондықтан бұл сандар Пифагордың жұп сандары деп аталған. IX ғасырда өмір сүрген араб математигі ибн Курра Сабит (836 - 901) достас сандарды анықтауға арналған тәсіл тапқан. Мысалмен түсіндірейік. 220 мен 284 сандарының бөлгіштерін табайық. 220 санының бөлгіштері: 1; 2; 4; 5; 10; 11; 20; 22; 44; 55; 110. 284 санының бөлгіштері: 1; 2; 4; 71; 142. 220 санының бөлгіштерінің қосындысын табайық: 1+2+4+5+10+11+20+22+44+55+110=284. 284 санының бөлгіштерінің қосындысын табайық: 1+2+4+71+142= 220 Қорытынды: 220 санының бөлгіштерінің қосындысы 284 санына, ал 284 санының бөлгіштерінің қосындысы 220 санына тең болды, сонда 220 және 284 сандары достас сандар болды. Күні бүгінге дейін достас сандар жиынтығы 1000 жұптан асты, оның ішінде тіпті 25 таңбалы достас сандар жұбы бар. Бұл жиынтықтың 13 жұбы 1 мен 100000-ның арасында орналасқан.
«Қарақұм жалпы білім беретін мектеп» КММ «Сандар арасындағы заңдылықтар» Дайындаған: Оңғалиева Дана 2022-2023 оқу жылы |
