|
|
Рабочая тетрадь 1 СоколоваАС. Рабочая тетрадь 1
3. Задания
|
1.
|
Задача:
|
|
Используя кодирование с избытком, закодируйте следующее сообщение: 00111011, троированием битов.
|
Решение:
|
|
000 000 111 111 111 000 111 111
|
Ответ:
|
|
000 000 111 111 111 000 111 111
|
2.
|
Задача:
|
|
В предположении, что в трех идущих подряд битах не может быть более одной ошибки, восстановите следующее сообщение: 001011010110011010001111 .
|
Решение:
|
|
до
|
101
|
011
|
111
|
001
|
111
|
101
|
001
|
111
|
после
|
111
|
000
|
111
|
000
|
111
|
111
|
000
|
111
|
результат
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
|
Ответ:
|
|
10101101
|
3.
|
Задача:
|
|
В сообщении троировались байты (символы таблицы ASCII). Было получено следующее сообщение:
CCzoYomdmppSuRutptweeQrr__*RssacciBieeenn%Fccjee .
Восстановите исходное сообщение.
|
|
Решение:
|
|
C o m p u t e r _ s c i e n c e
|
Ответ:
|
|
Computer_science
|
1. Теоретический материал
|
Определим расстояние между символами кода. Пусть каждый символ кодируется последовательностью из N битов 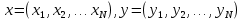 . Расстояние . Расстояние 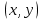 определим следующей формулой [1]: определим следующей формулой [1]:
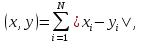
где 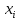 и и 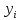 принимают значения ноль или единица. Представленная формула позволяет определить расстояние между представлениями символов в виде кода. Тогда n количество ошибок, которые можно исправить, если определить наименьшее из расстояний d определяется по следующей формуле: принимают значения ноль или единица. Представленная формула позволяет определить расстояние между представлениями символов в виде кода. Тогда n количество ошибок, которые можно исправить, если определить наименьшее из расстояний d определяется по следующей формуле:
d ≥ 2n + 1.
Обобщим, идея метода состоит в определении количество отличных битов в кодовом представлении символов. Далее из всех выбирается наименьшее значение – это значение с использованием формулы d ≥ 2n + 1, позволяет найти количество ошибок, которые можно исправить. То есть, чтобы исправлять 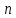 ошибок, необходимо учитывать расстояние между любыми символами, которое должно быть не меньше ошибок, необходимо учитывать расстояние между любыми символами, которое должно быть не меньше 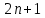 . .
|
2. Пример
|
1.
|
Задача:
|
|
Даны следующие коды:
|
буква
|
A
|
B
|
C
|
код
|
00000
|
11100
|
00111
|
|
Найти расстояние между кодами для B и C.
|
Решение:
|
|
Посчитаем количество различных бит в кодах для B и C . Четыре бита различны.
|
|
|
|
Ответ:
|
|
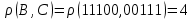
|
2.
|
Задача:
|
|
Сколько ошибок можно исправить при использовании кодов из предыдущего примера?
|
Решение:
|
|
Найдём минимальное расстояние 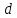 между кодами. между кодами.
A
|
0
|
0
|
0
|
0
|
0
|
|
B
|
1
|
1
|
1
|
0
|
0
|
|
C
|
0
|
0
|
1
|
1
|
1
|
B
|
1
|
1
|
1
|
0
|
0
|
|
C
|
0
|
0
|
1
|
1
|
1
|
|
A
|
0
|
0
|
0
|
0
|
0
|
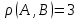
|
|
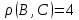
|
|
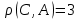
|
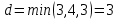
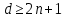 → → 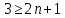
Из этого условия найдем 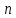 . Получим . Получим 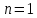 . Таким образом, всегда можно исправить 1 ошибку. . Таким образом, всегда можно исправить 1 ошибку.
|
Ответ:
|
|
Можно гарантированно исправить 1 ошибку
|
3. Задания
|
1.
|
Задача:
|
|
Даны следующие коды:
|
буква
|
A
|
B
|
C
|
код
|
0101010
|
1010100
|
0011110
|
|
Найти расстояние между кодами для B и C.
|
Решение:
|
|
1010100
0011110
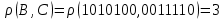
|
Ответ:
|
|
3
|
2.
|
Задача:
|
|
Верны ли следующие утверждения:
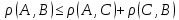 , ,
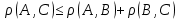 , ,
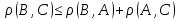 ? ?
|
Решение:
|
|
Да, утверждения верны
|
Ответ:
|
|
Да, утверждения верны
|
3.
|
Задача:
|
|
Сколько ошибок можно гарантированно исправить при использовании кодов из задачи1?
|
Решение:
|
|
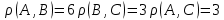
d = min(6, 3, 3) = 3
3 >= 2n + 1
n <= 1
|
Ответ:
|
|
1
| |
|
|
 Скачать 359.49 Kb.
Скачать 359.49 Kb.