|
|
ОТУ_5_лабораторная_работа. Работа 5 Построение логарифмических частотных характеристик систем автоматического регулирования
Работа № 5
Продолжительность работы – 4 часов.
Цель работы
Получение навыков расчета частотных характеристик элементарных линейных звеньев. Исследование особенностей построения частотных характеристик (вещественных, мнимых, амплитудно-частотных, фазовых) и реальных и идеальных (асимптотических) логарифмических частотных характеристик элементарных линейных звеньев, построение характеристик с применением пакета символьной математики Mathcad.
Теоретическое обоснование
При практических расчетах СУ удобно использовать частотные характеристики, построенные в логарифмических координатах. Такие характеристики называют логарифмическими. Они имеют наименьшую кривизну и могут быть приближенно заменены ломанными линиями, составленными из нескольких отрезков. Причем эти отрезки в большинстве случаев удается построить без громоздких вычислений, при помощи некоторых простых правил. Кроме того в логарифмической системе координат легко находятся характеристики различных соединительных элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.
 Логарифмическая частотная характеристика (ЛАЧХ) – частотная характеристика в логарифмическом масштабе. Логарифмическая частотная характеристика (ЛАЧХ) – частотная характеристика в логарифмическом масштабе.
L( ), ДБ Октава ), ДБ Октава
20
10
-1 0 1 2 lg
0,1 0,5 1 2 5 10 100 
-10 Декада
-20
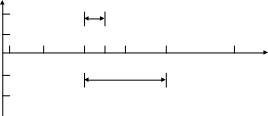
За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервалы частоты, заключенный между произвольным значением ωi и его десятикратным значением 10ωi. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1.
Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)
L(ω)=20lg{W(ω)}
Ординаты которой измеряют в логарифмических единицах – Белах или децибелах(дБ).
1 Бел = 10 дБ
1 Бел – единица измерения мощностей двух сигналов.
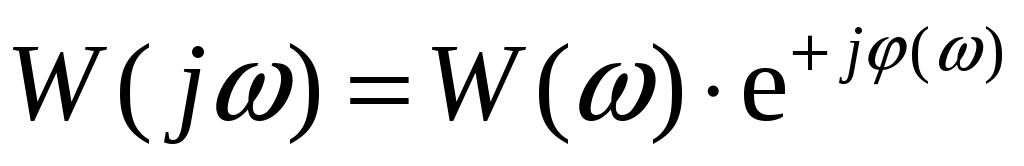
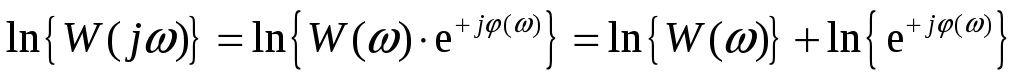
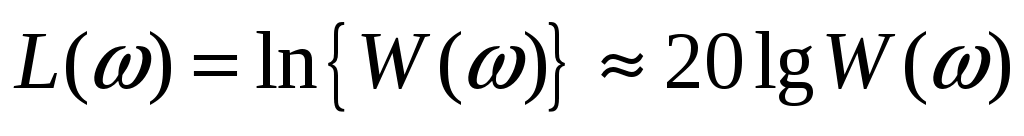
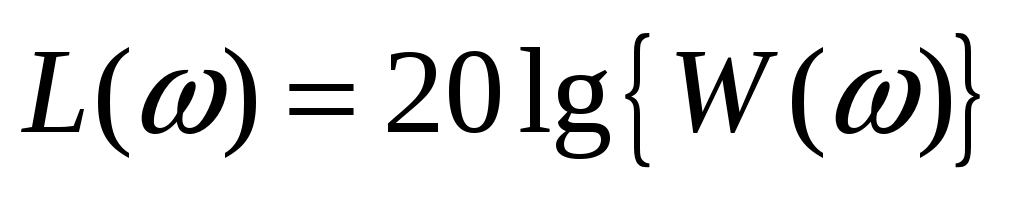 - ЛАЧХ - ЛАЧХ
из передаточной функции 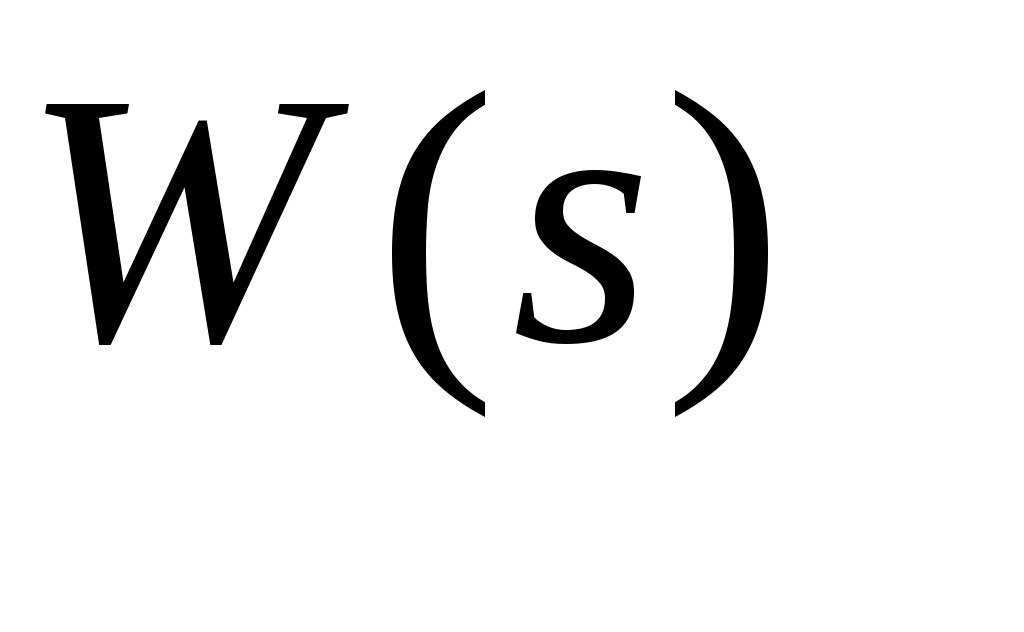 системы заменой комплексной переменной s на системы заменой комплексной переменной s на 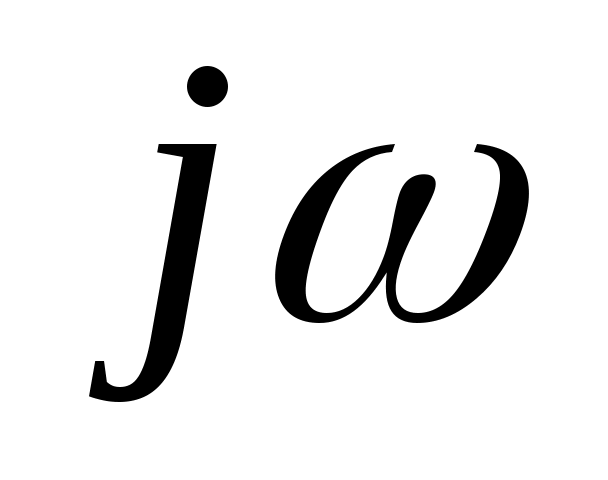 может быть получена функция, называемая комплексным коэффициентом передачи системы может быть получена функция, называемая комплексным коэффициентом передачи системы
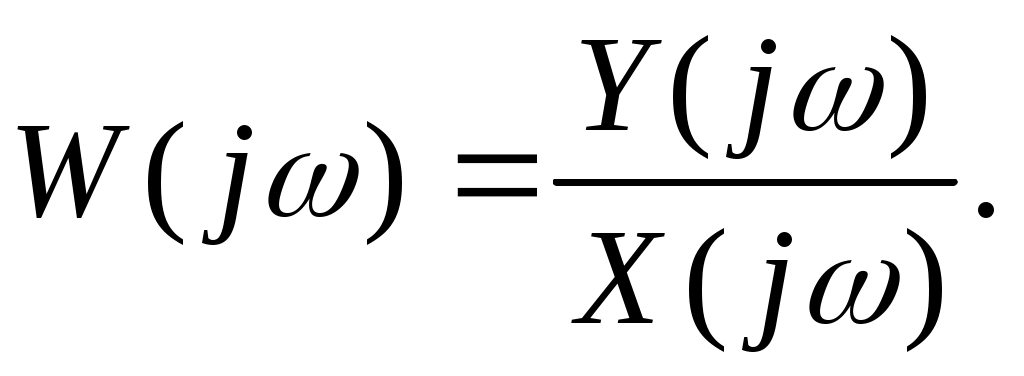
комплексный коэффициент передачи может быть представлен в двух видах:
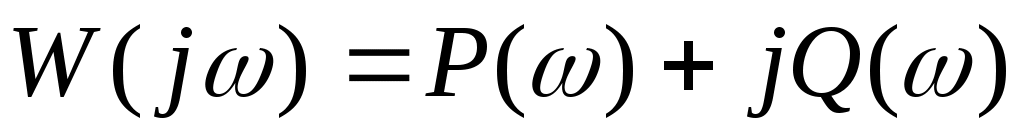 , ,
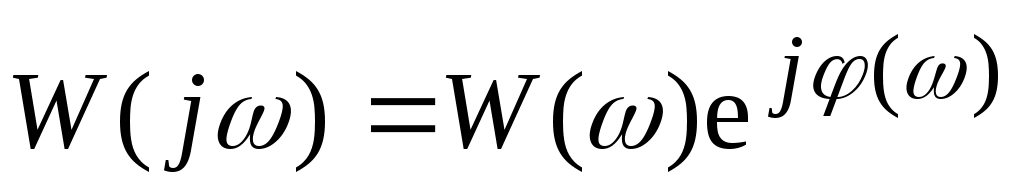 , ,
где 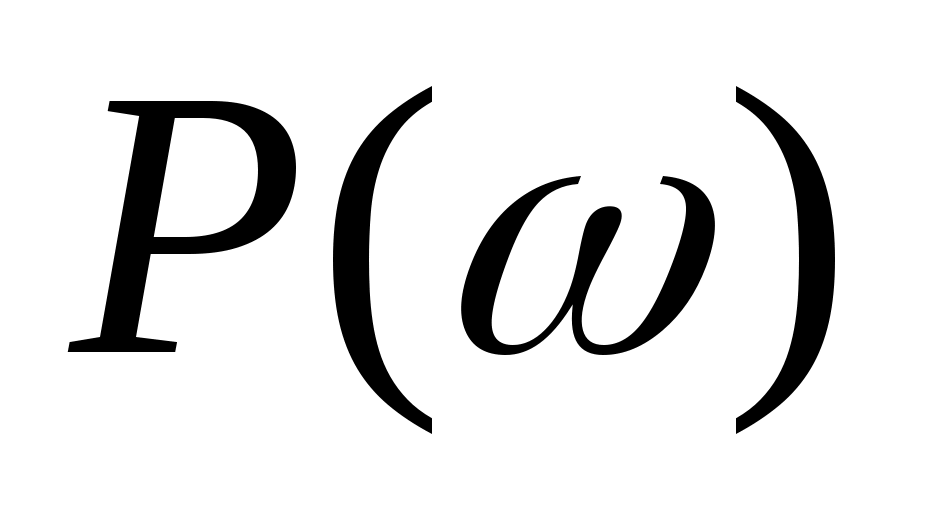 и и 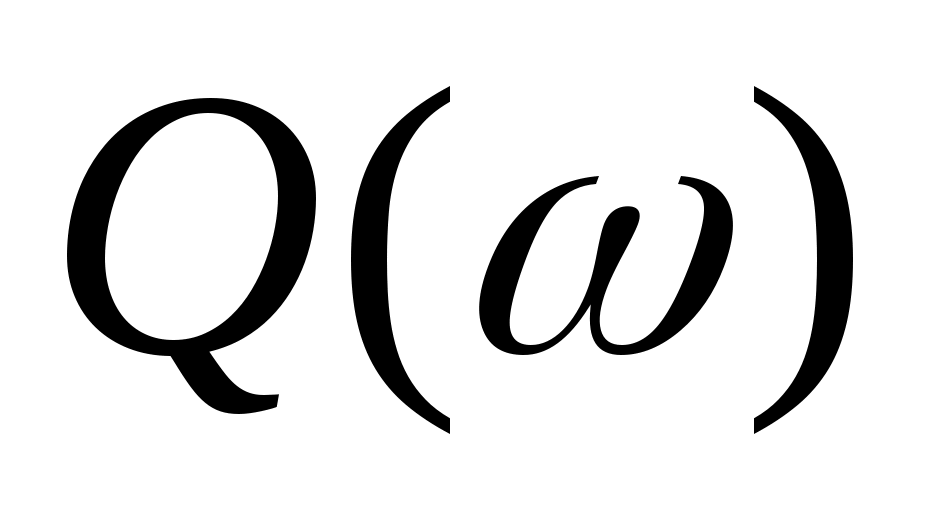 - вещественная и мнимая частотные характеристики системы, - вещественная и мнимая частотные характеристики системы,
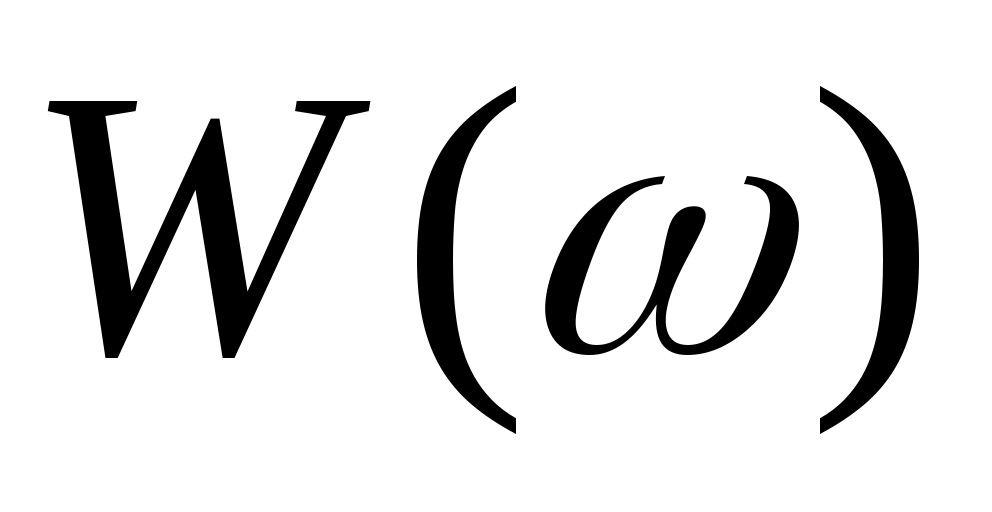 и и 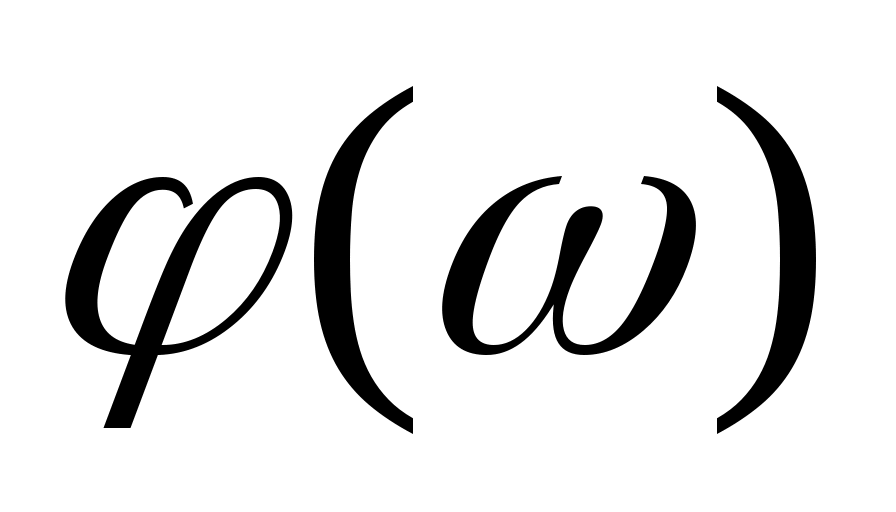 - амплитудно-частотная и фазово-частотная характеристики системы. - амплитудно-частотная и фазово-частотная характеристики системы.
Связь между этими частотными характеристиками определяется формулами
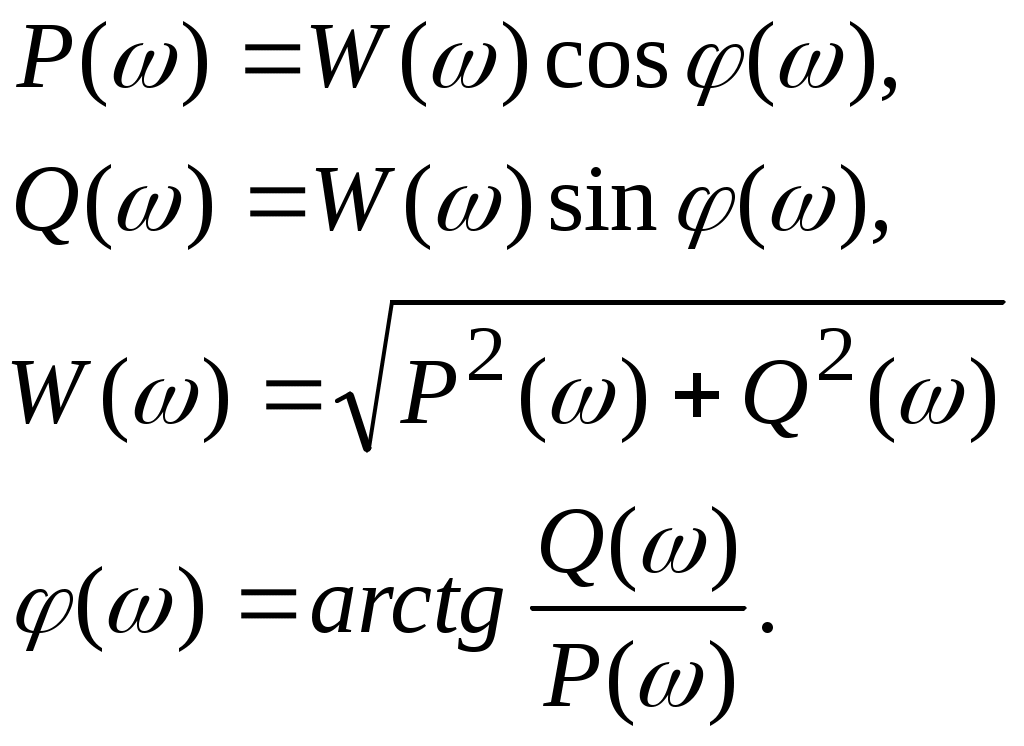
Амплитудно-частотная характеристика системы является модулем комплексного коэффициента передачи 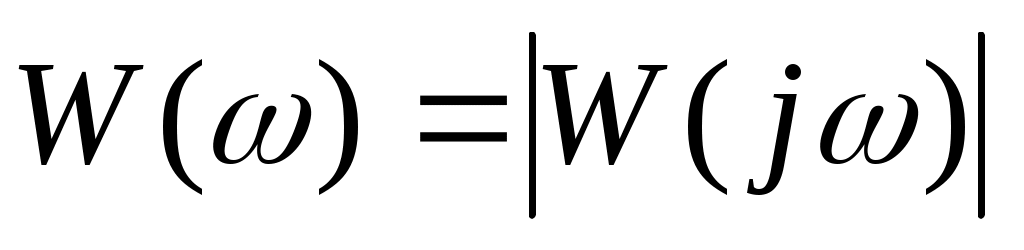 , а фазовая частотная характеристика - его аргументом , а фазовая частотная характеристика - его аргументом 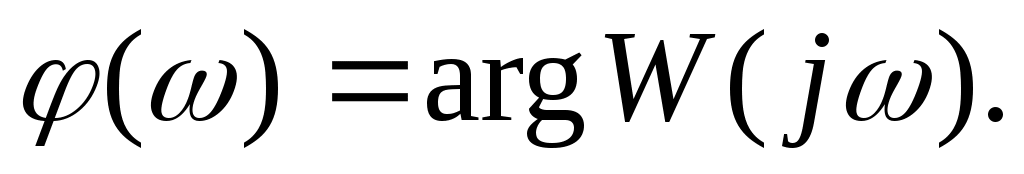
В частотной области динамические свойства линейных звеньев характеризуются амплитудно-частотной 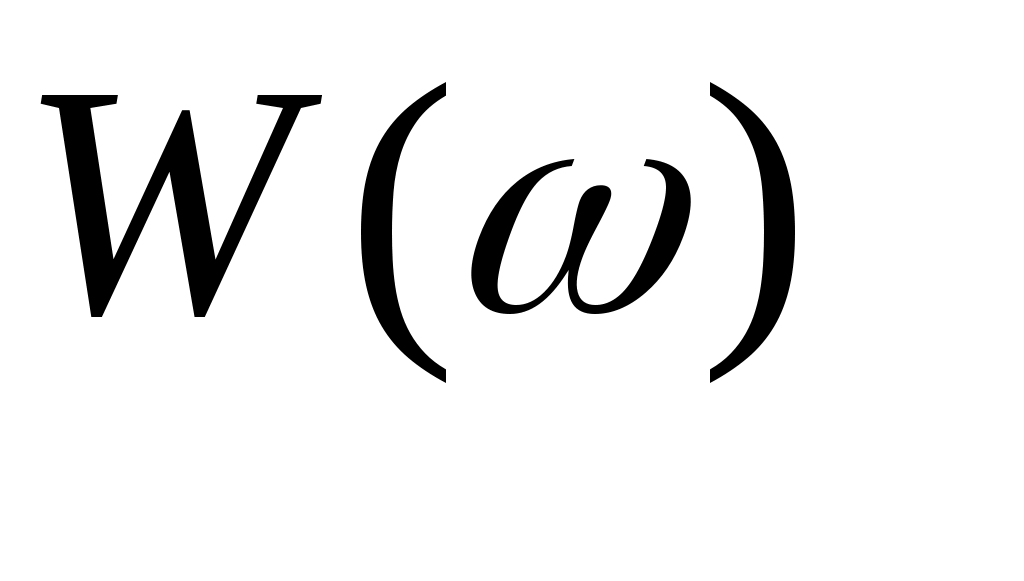 (АЧХ) и фазочастотной (АЧХ) и фазочастотной 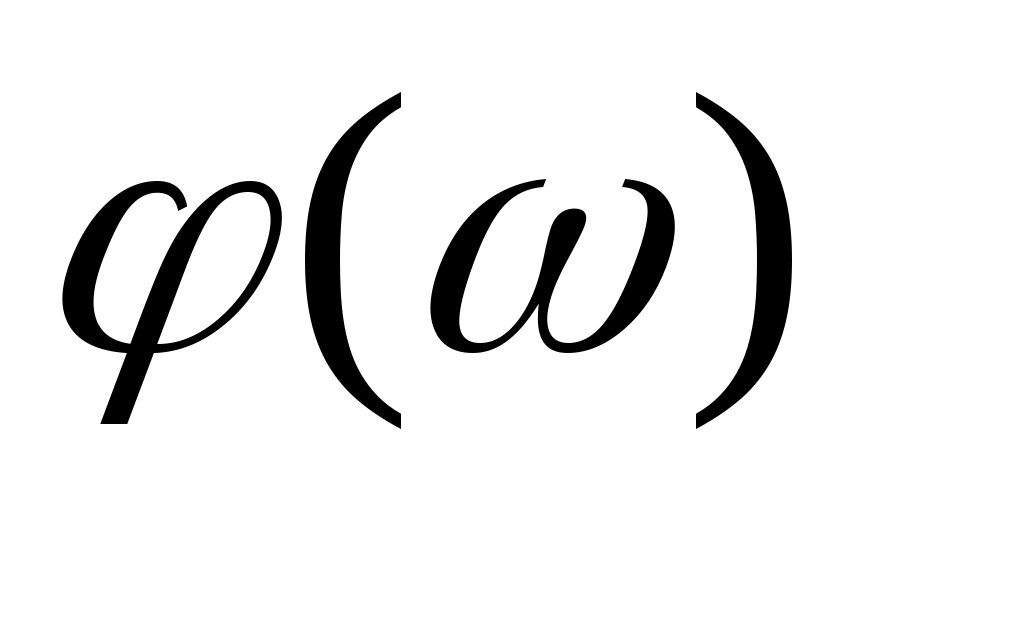 (ФЧХ) характеристиками. Эти характеристики связаны с передаточной функцией (ФЧХ) характеристиками. Эти характеристики связаны с передаточной функцией 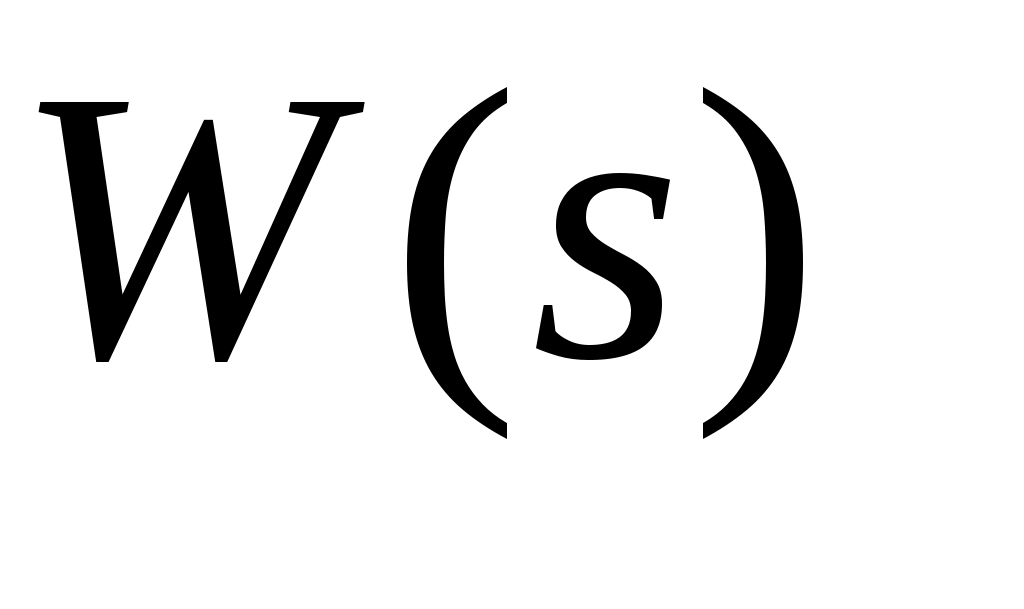 соотношениями соотношениями

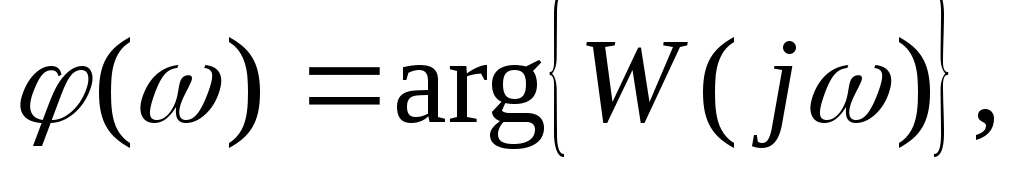
где 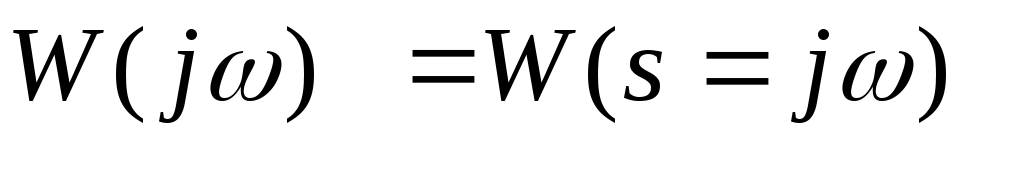 - комплексный коэффициент передачи, - комплексный коэффициент передачи,
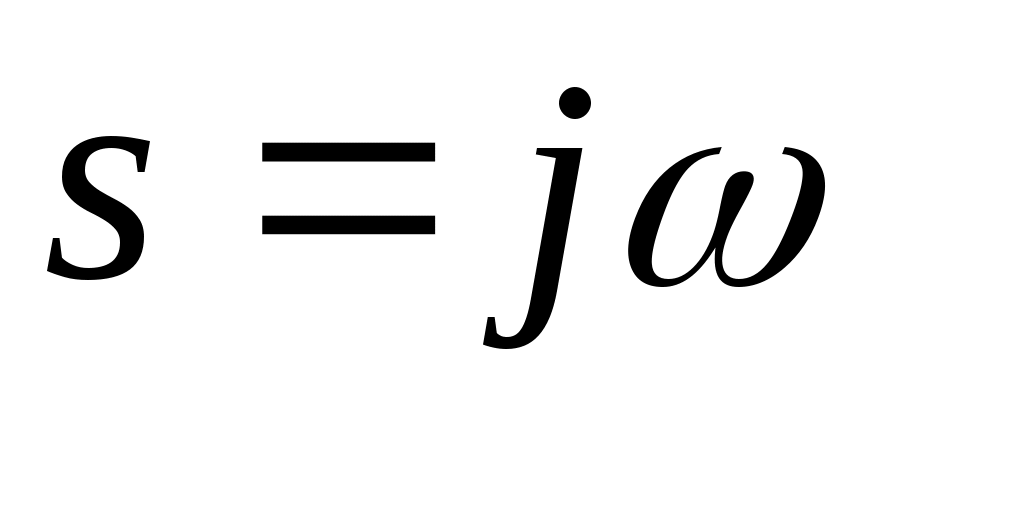 - комплексная переменная - комплексная переменная
При анализе и синтезе систем управления используются логарифмические частотные характеристики (ЛАЧХ).
Функция 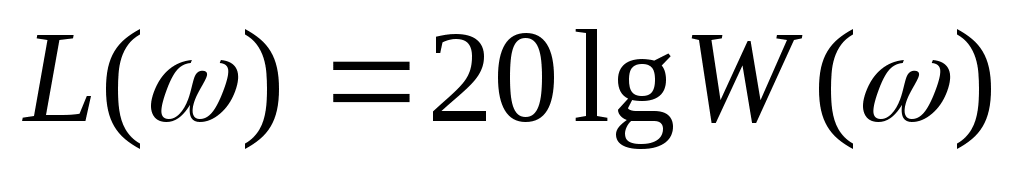 называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ). По оси абсцисс ЛАЧХ строится в десятичном масштабе частот называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ). По оси абсцисс ЛАЧХ строится в десятичном масштабе частот 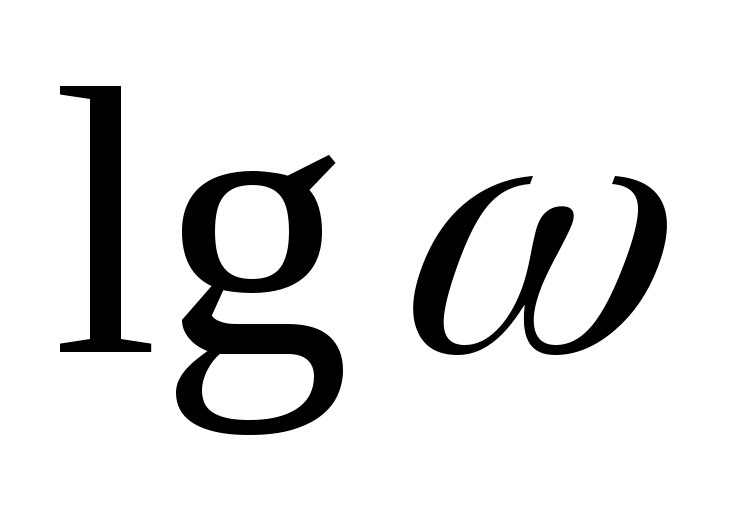 , а по оси ординат - , а по оси ординат - 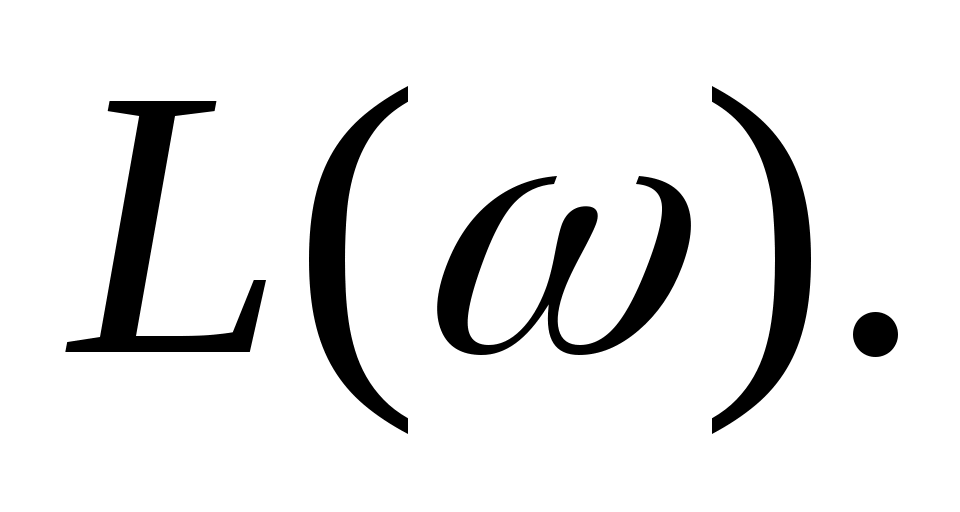 Единицей измерения Единицей измерения 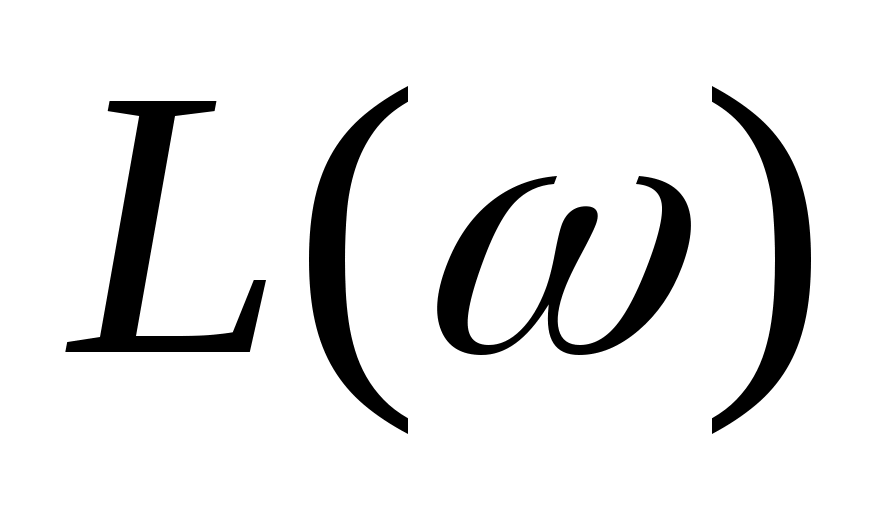 является децибел (дБ), а единицей измерения интервала частоты - декада. Декада - интервал частоты, на котором она изменяется в десять раз. является децибел (дБ), а единицей измерения интервала частоты - декада. Декада - интервал частоты, на котором она изменяется в десять раз.
Логарифмической фазочастотной характеристикой (ЛФЧХ) называется фазовая частотная характеристика 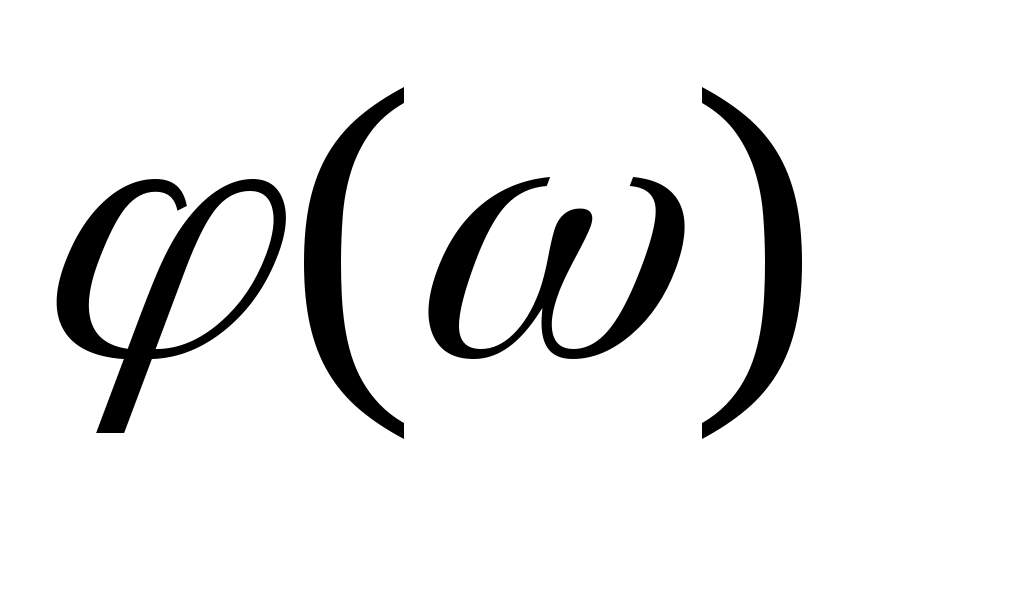 , построенная в десятичном масштабе частот lg ω. Логарифмическая фазовая частотная характеристика (ЛФЧХ) измеряется в радианах или градусах. , построенная в десятичном масштабе частот lg ω. Логарифмическая фазовая частотная характеристика (ЛФЧХ) измеряется в радианах или градусах.
Низкочастотная асимптота ЛАЧХ 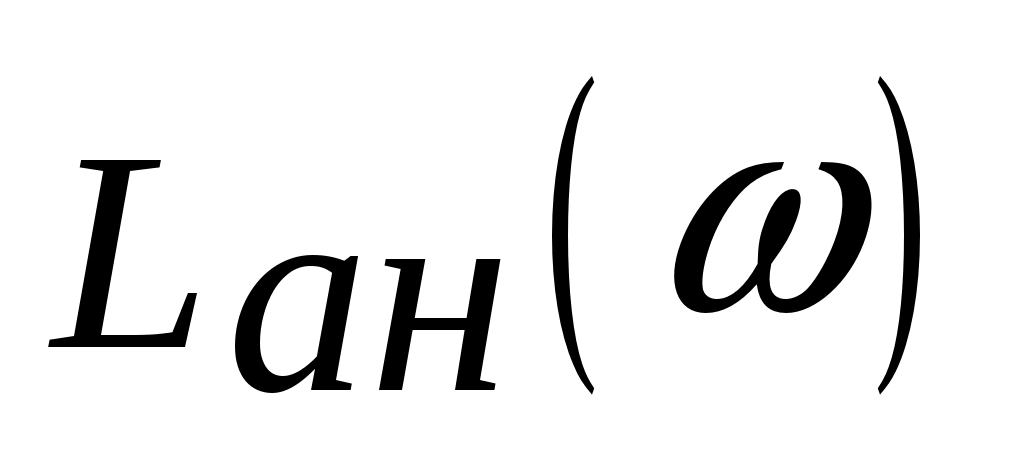 представляет собой предел представляет собой предел
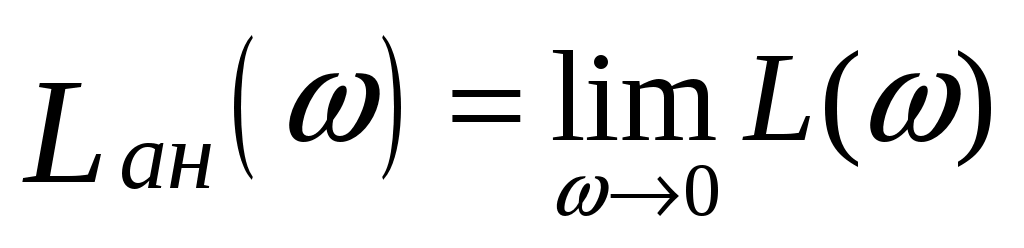
Высокочастотная асимптота ЛАЧХ 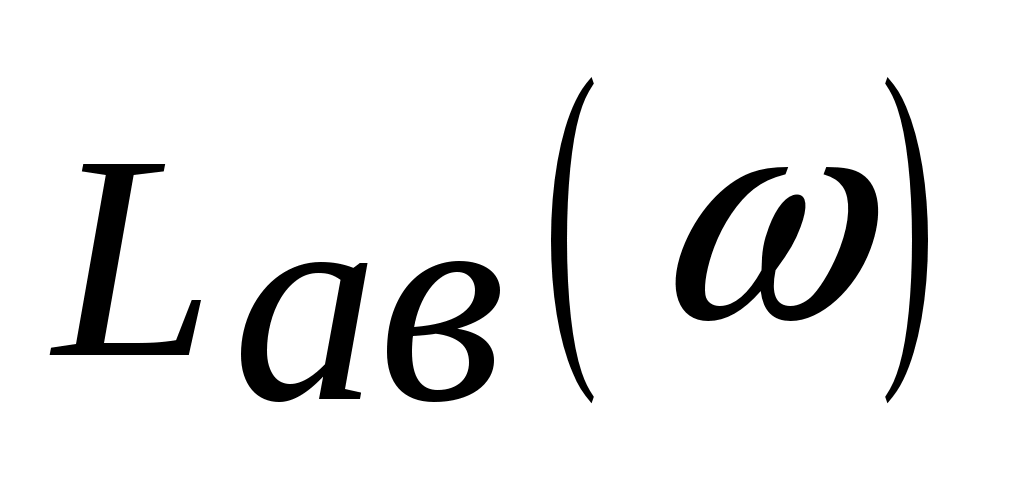 есть предел логарифмической АЧХ есть предел логарифмической АЧХ
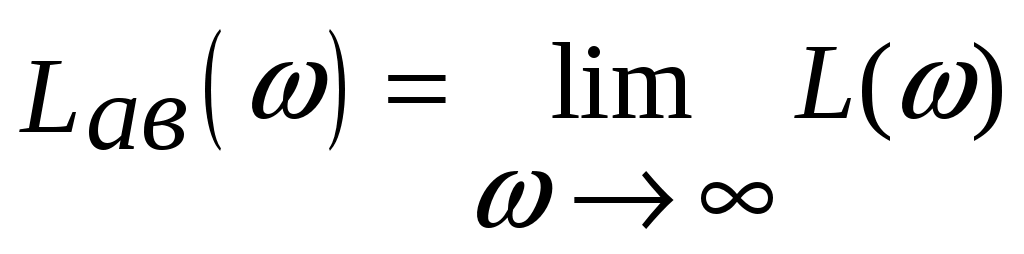
Асимптотической ЛАЧХ является характеристика, составленная из асимптот.
Разность между действительной 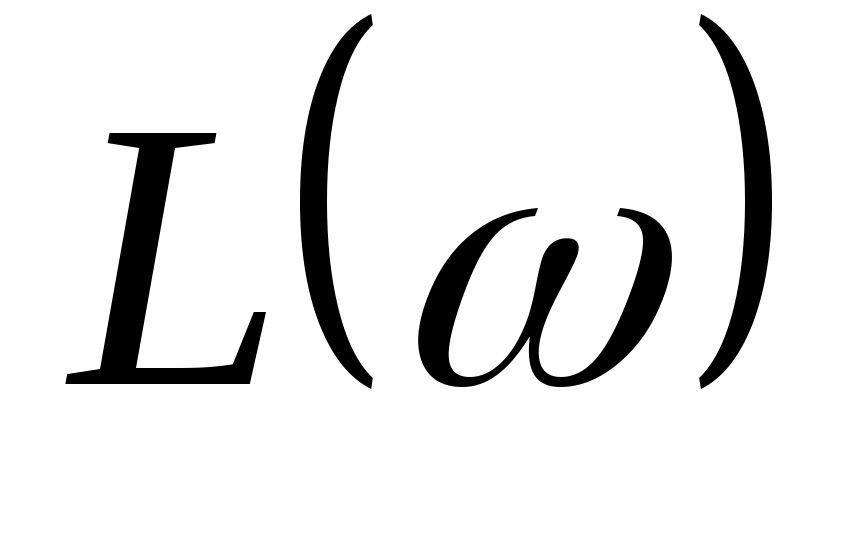 и асимптотической и асимптотической 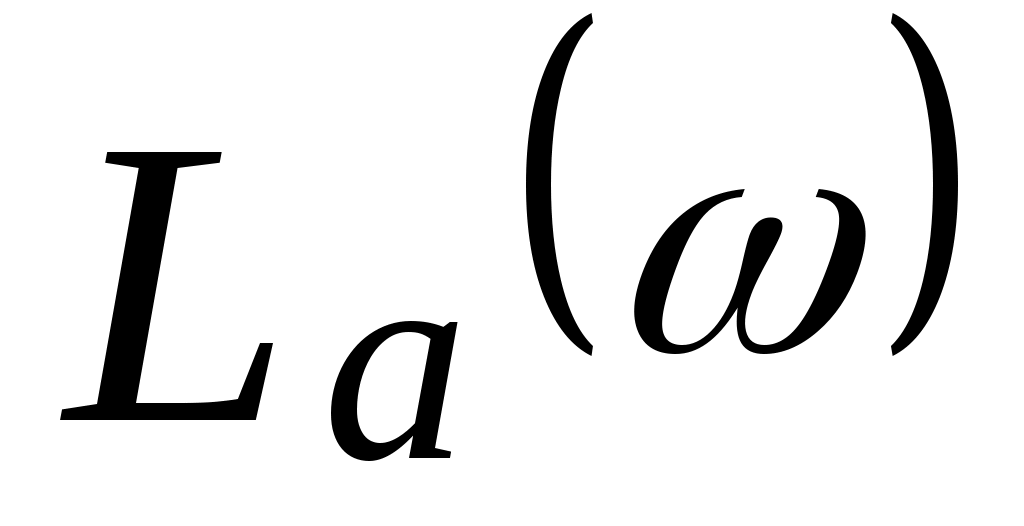 ЛАЧХ есть поправка ЛАЧХ есть поправка 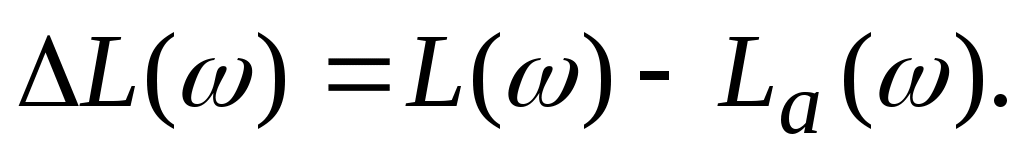
Частота 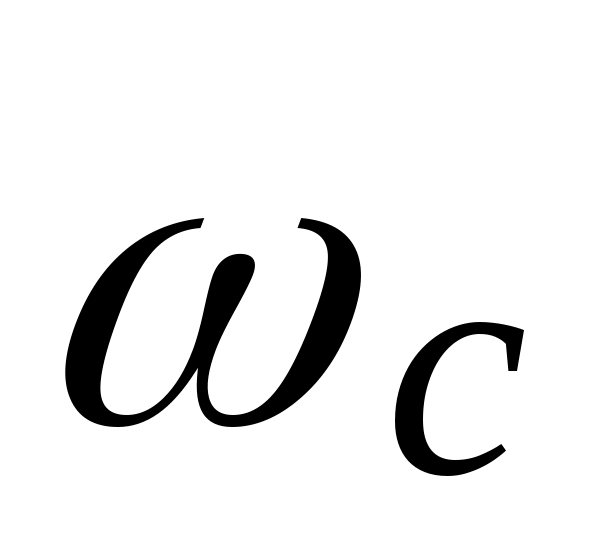 , на которой сопрягаются различные асимптоты, называются частотой сопряжения. , на которой сопрягаются различные асимптоты, называются частотой сопряжения.
Для ЛАЧХ, составленных из трех и более участков асимптот, существует несколько частот сопряжения ωс1, ωс2, ωс3, и т.д. Обычно частоты сопряжения нумеруются в порядке возрастания, т.е. ωс1<ωс2<ωс3<… Наибольшая разность 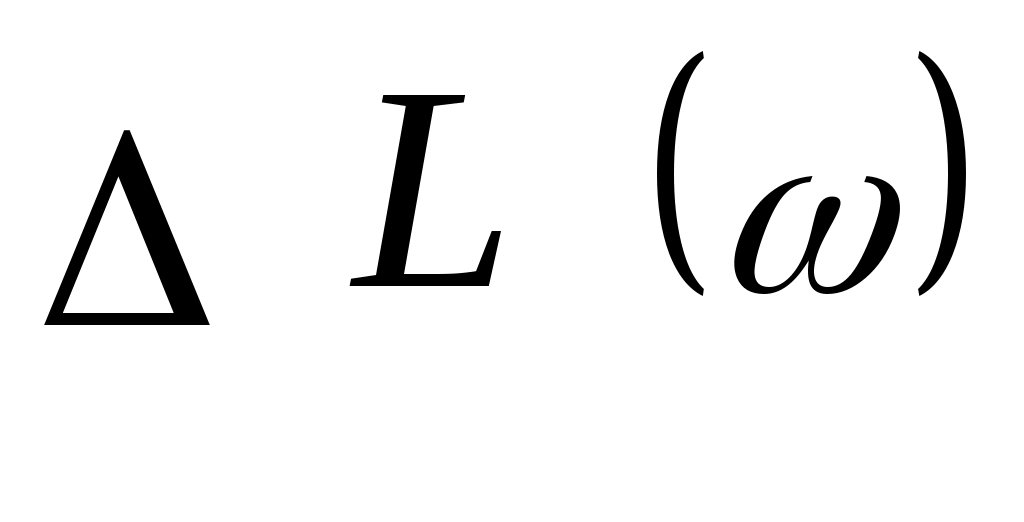 имеет место на частоте спряжения ωсi. Поэтому именно в ее окрестностях следует учитывать поправку. имеет место на частоте спряжения ωсi. Поэтому именно в ее окрестностях следует учитывать поправку.
Построение логарифмических частотных характеристик сложных систем
Методика построения ЛАЧХ сводится к следующим этапам:
ЛАЧХ строится по W(s) разомкнутой части системы.
Определить коэффициент пропорциональности системы К и 20lgК ;
Определить частоты сопряжения элементарных звеньев и определить lgwс, где wс- соответствующие частоты сопряжения;
Расположить элементарные звенья по возрастанию частот сопряжения wс и lgwс;
Задаться наклоном +20дБ/дек или -20дБ/дек и кратным им наклонам в масштабе координатной плоскости;
Если передаточная функция разомкнутой части системы содержит n одинаковых звеньев, то наклон ЛАЧХ будет увеличен в n раз.
Методику построения ЛАЧХ системы можно разделить на четыре типа по особенностям системы управления:
Ниже представлены частотные характеристики и асимптотические ЛАЧХ и методика их расчета для типовых звеньев.
Пропорциональное звено
Передаточная функция пропорционального звена может быть представлена выражением
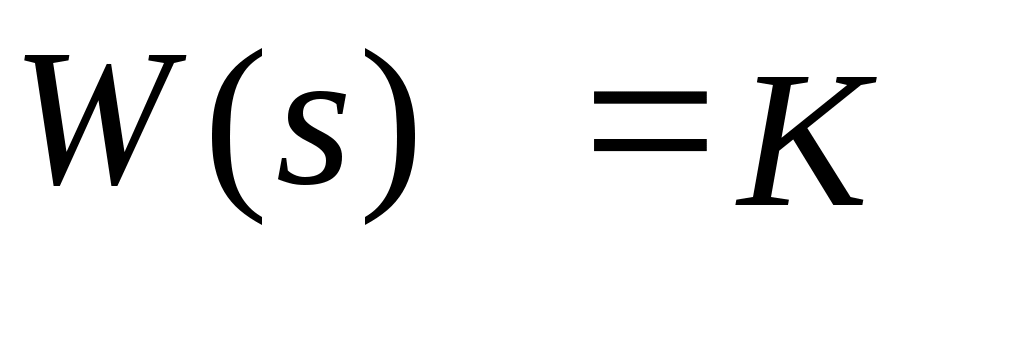 (4.1.) (4.1.)
Из формулы (4.1.), выполнив замену 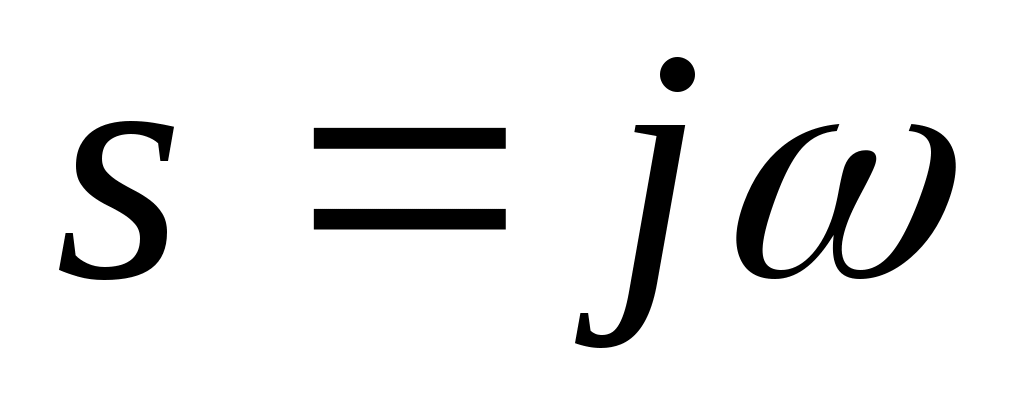 , можно найти комплексный коэффициент передачи пропорционального звена , можно найти комплексный коэффициент передачи пропорционального звена 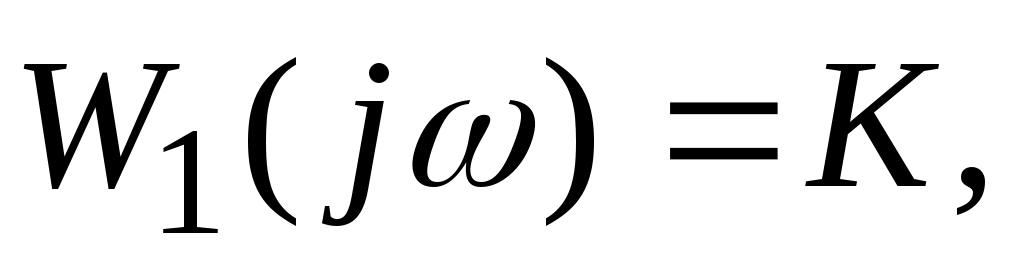 вещественную частотную характеристику вещественную частотную характеристику 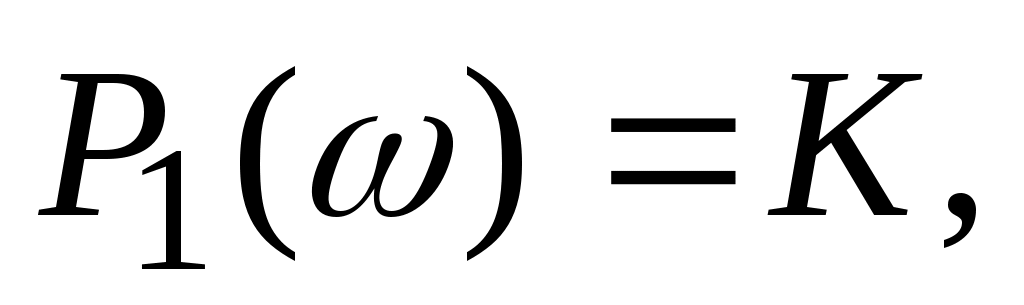 мнимую частотную характеристику мнимую частотную характеристику 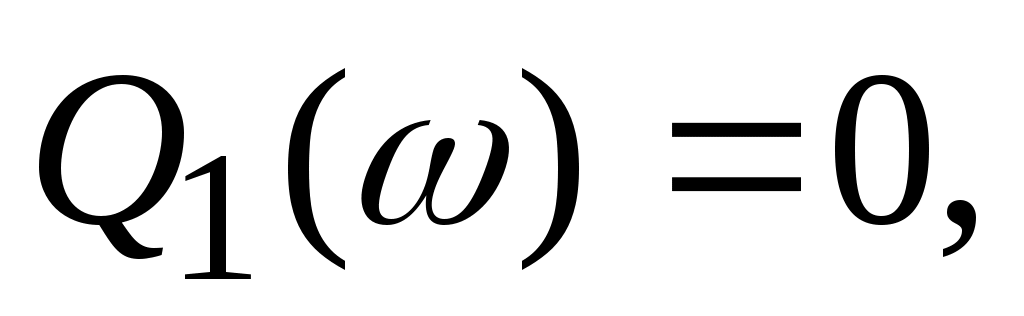 амплитудно-частотную характеристику амплитудно-частотную характеристику 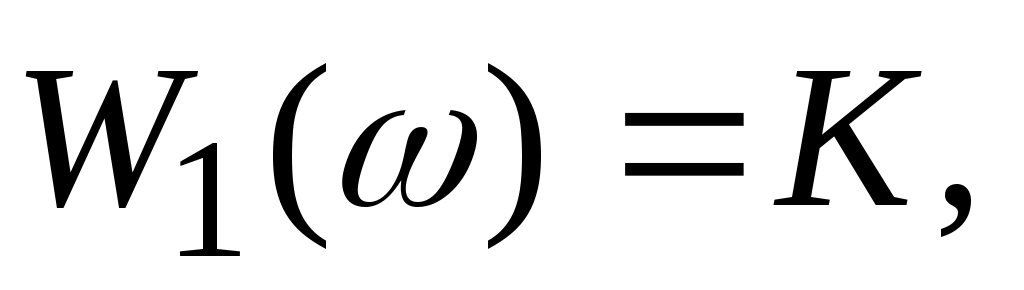 и фазовую частотную характеристику и фазовую частотную характеристику 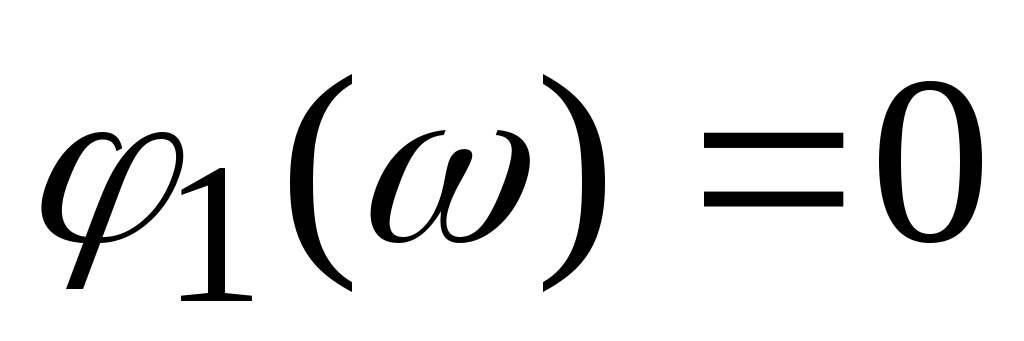 . .
Действительная 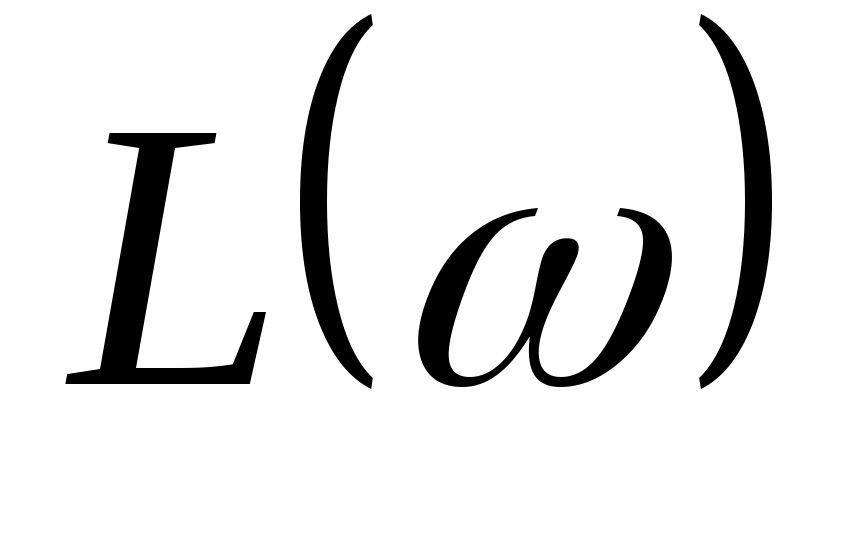 логарифмическая амплитудно-частотная характеристика пропорционального звена будет равна логарифмическая амплитудно-частотная характеристика пропорционального звена будет равна 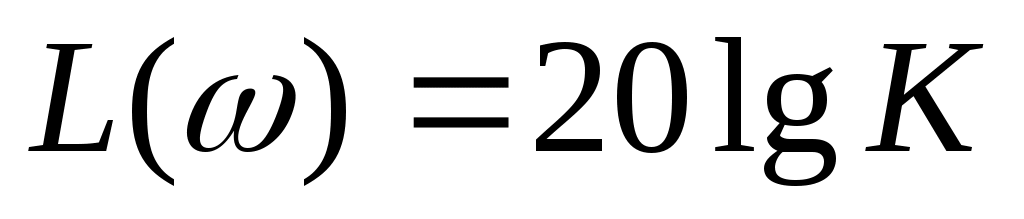 . .
Она совпадает с асимптотической логарифмической амплитудно-частотной характеристикой пропорционального звена равна
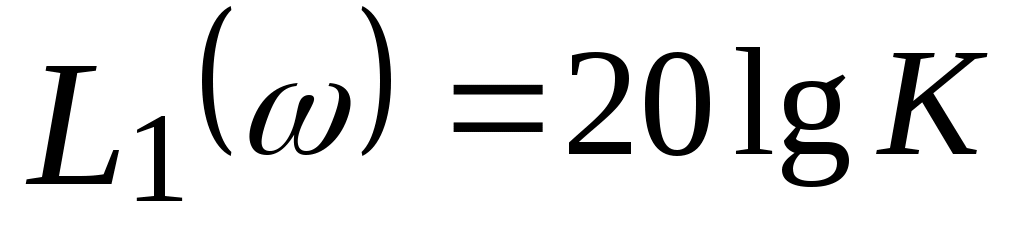 , ,
Логарифмическая фазочастотная характеристика пропорционального звена равна
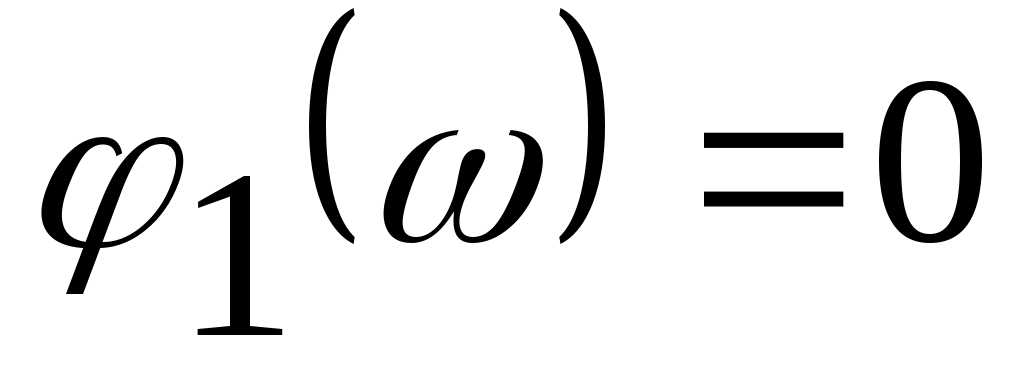 . .
График 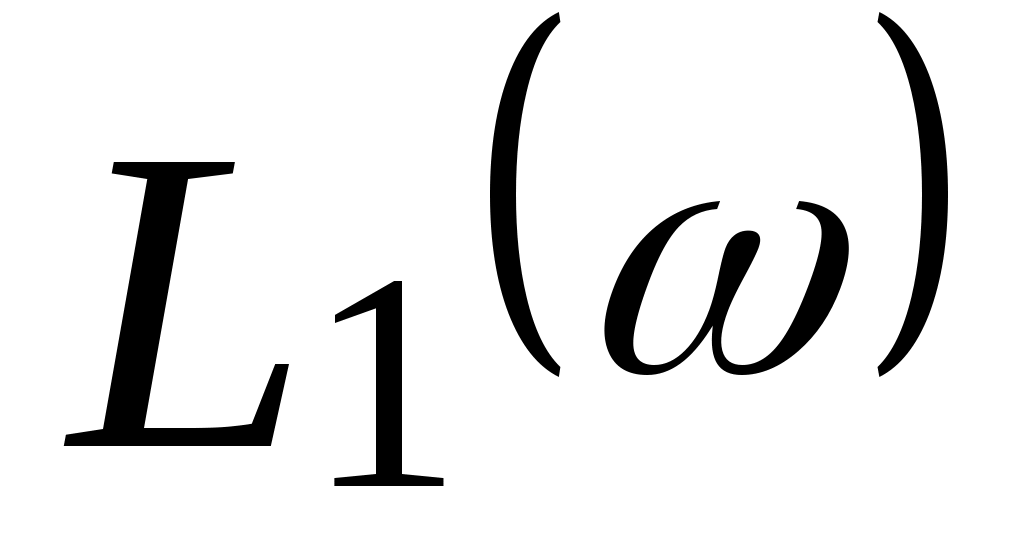 показан на рис. 5.1. Для этого звена асимптотическая ЛАЧХ показан на рис. 5.1. Для этого звена асимптотическая ЛАЧХ 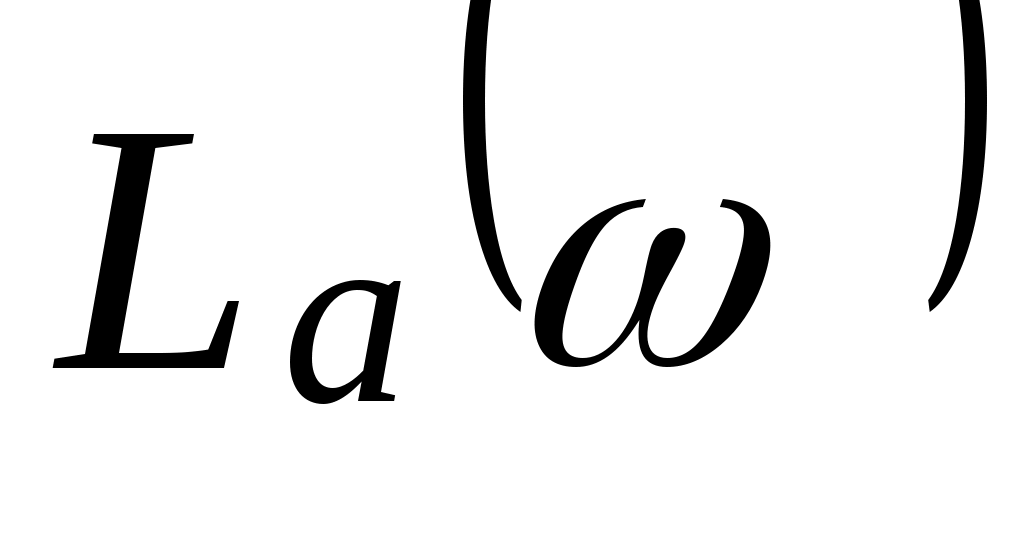 совпадает с истинным совпадает с истинным 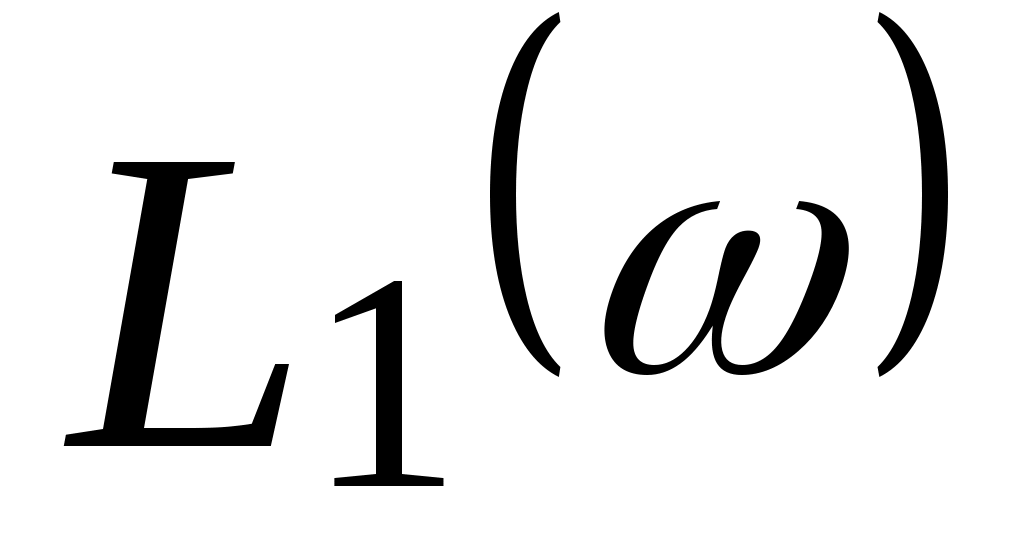 во всем диапазоне частот ω. во всем диапазоне частот ω.
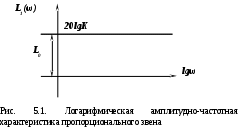
Для определения коэффициента усиления нужно измерить значение 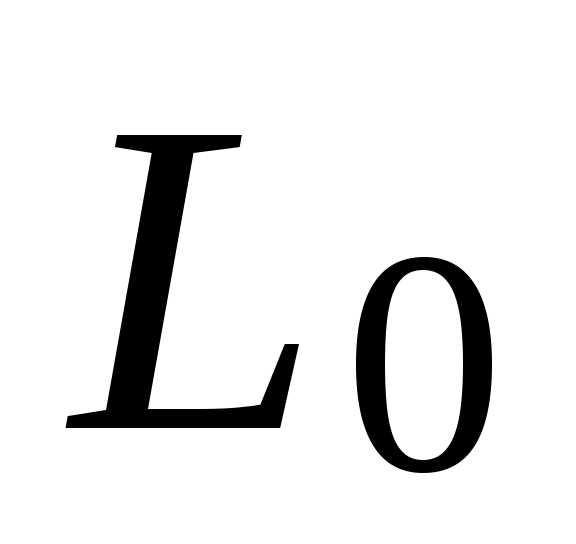 в децибелах (дБ) и записать соотношение в децибелах (дБ) и записать соотношение 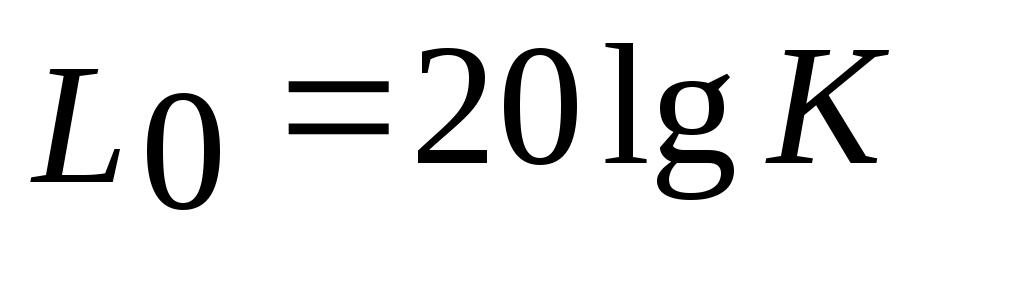 , из которого можно найти значение коэффициента пропорциональности , из которого можно найти значение коэффициента пропорциональности 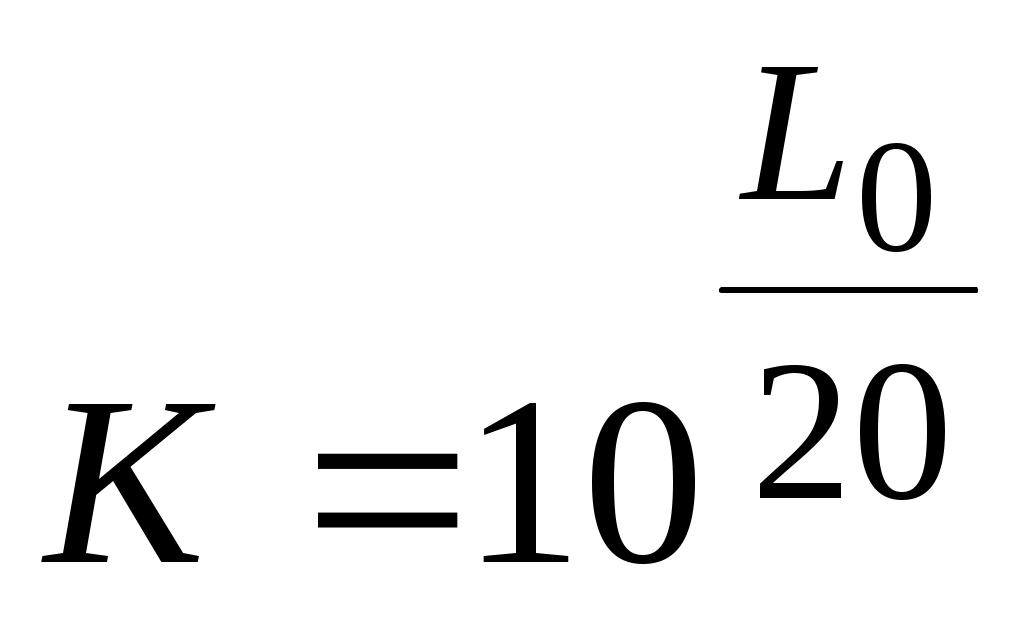 . .
Логарифмическая фазочастотная характеристика пропорционального звена совпадает с осью абсцисс (рис.5.2).

Интегрирующее звено
Передаточная функция интегрирующего звена равна
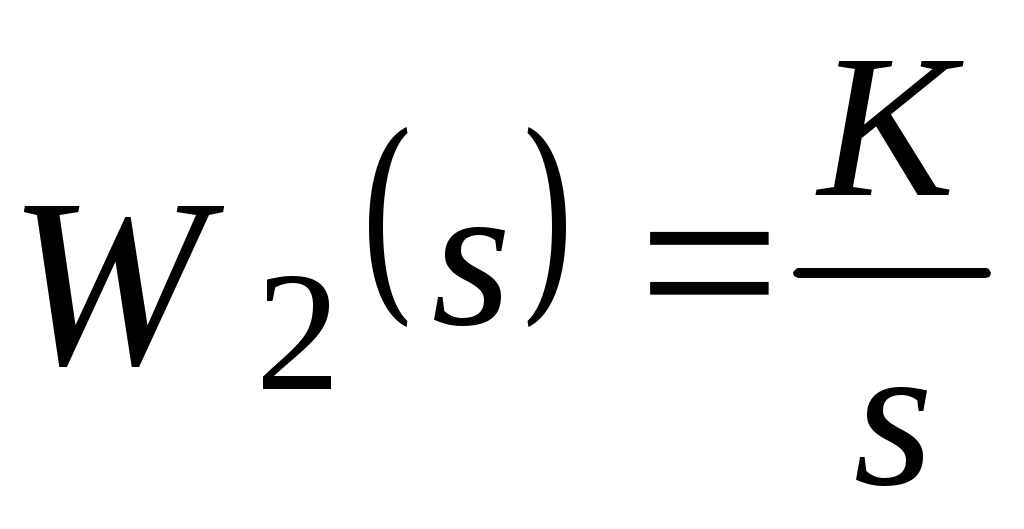 . .
Из формулы передаточной функции интегрирующего звена, выполнив замену 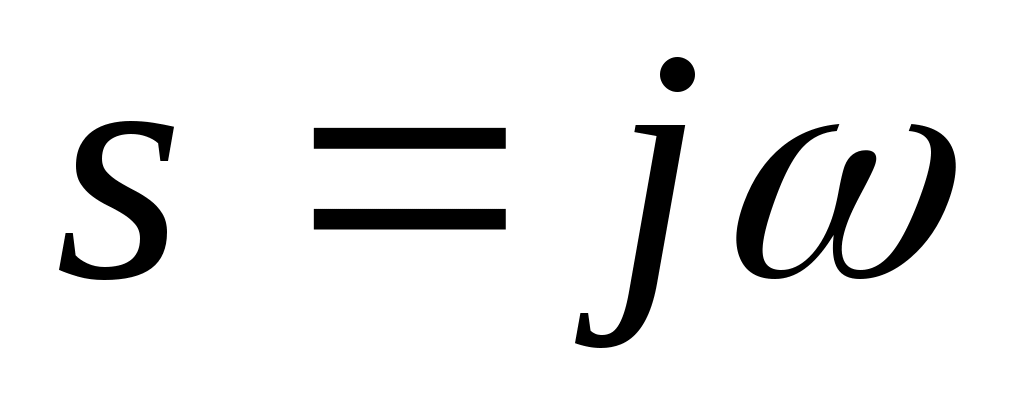 , можно найти , можно найти
комплексный коэффициент передачи
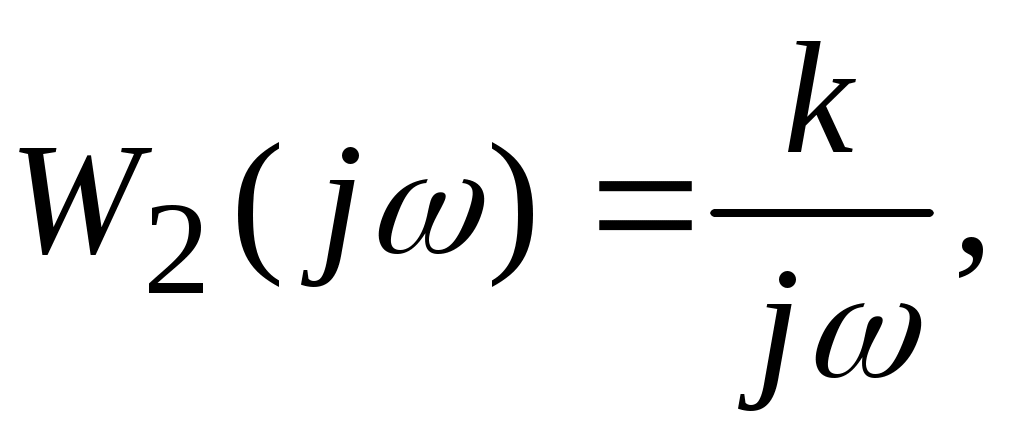
вещественную частотную характеристику
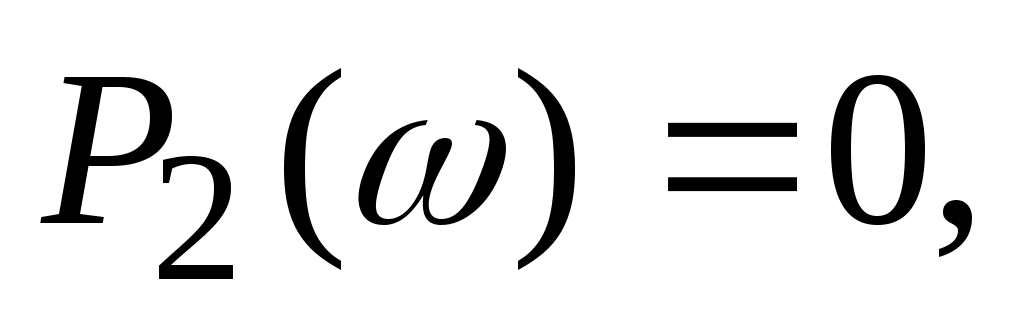
мнимую частотную характеристику
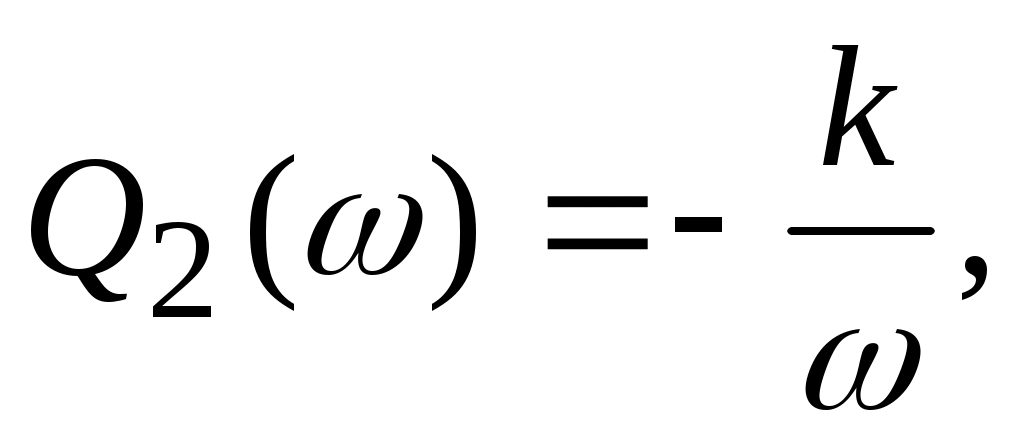
амплитудно-частотную характеристику
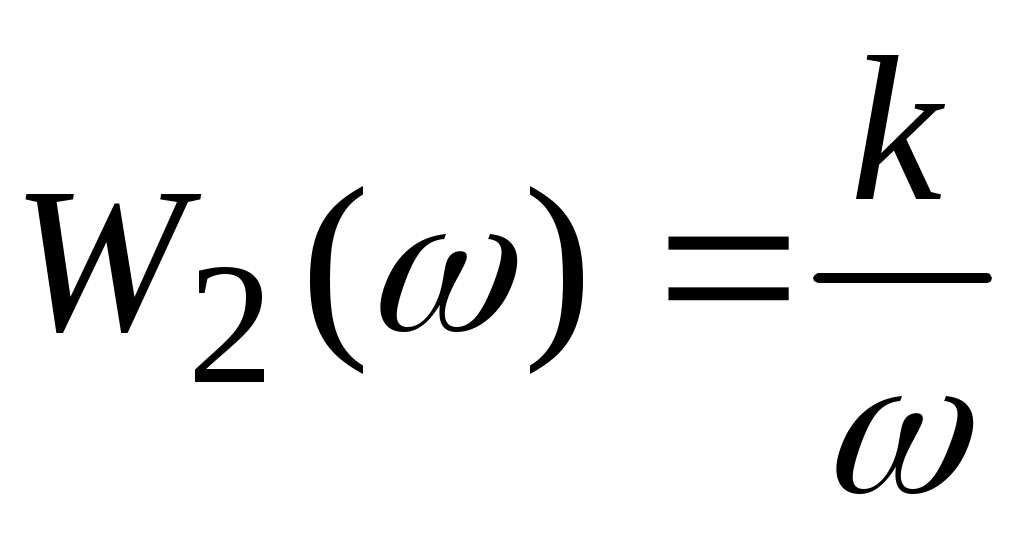
и фазовую частотную характеристику
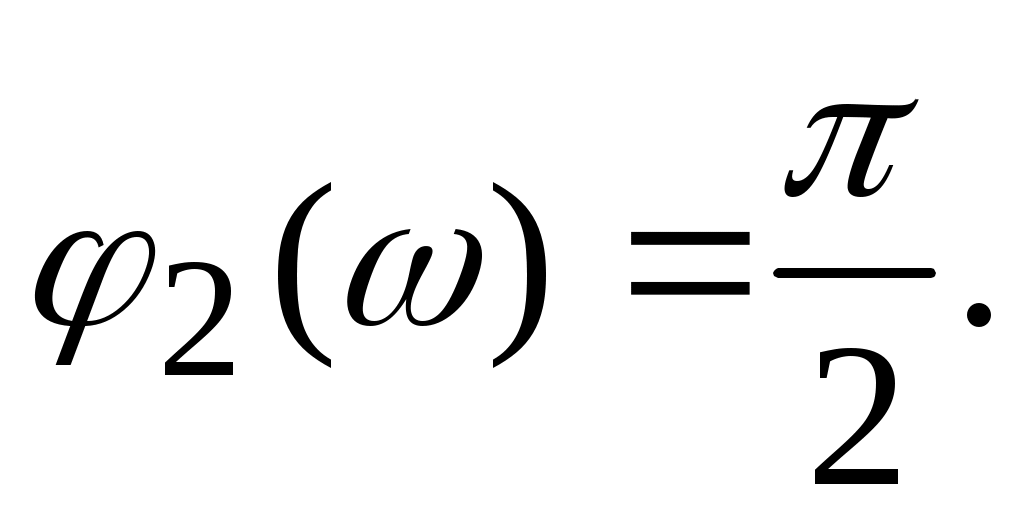
Годограф амплитудно-фазовой частотной характеристики (АФЧХ) интегрирующего звена, зависимость Q() от P(), представляет собой прямую линию, совпадающую с мнимой осью.
Логарифмическая амплитудно-частотная характеристика интегрирующего звена равна
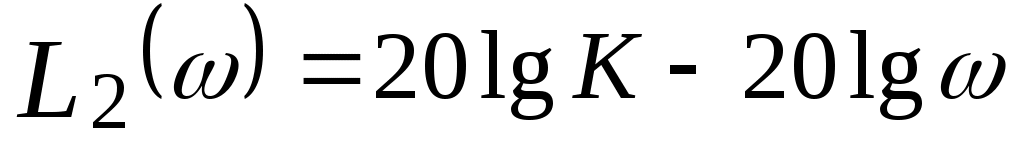 . .
Логарифмическая фазочастотная характеристика интегрирующего звена равна
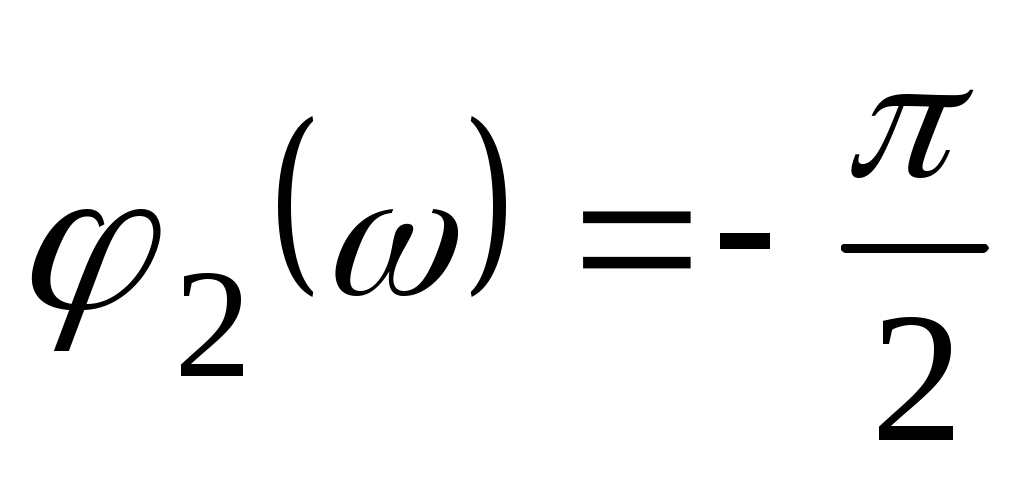
На рис. 5.3. представлен график 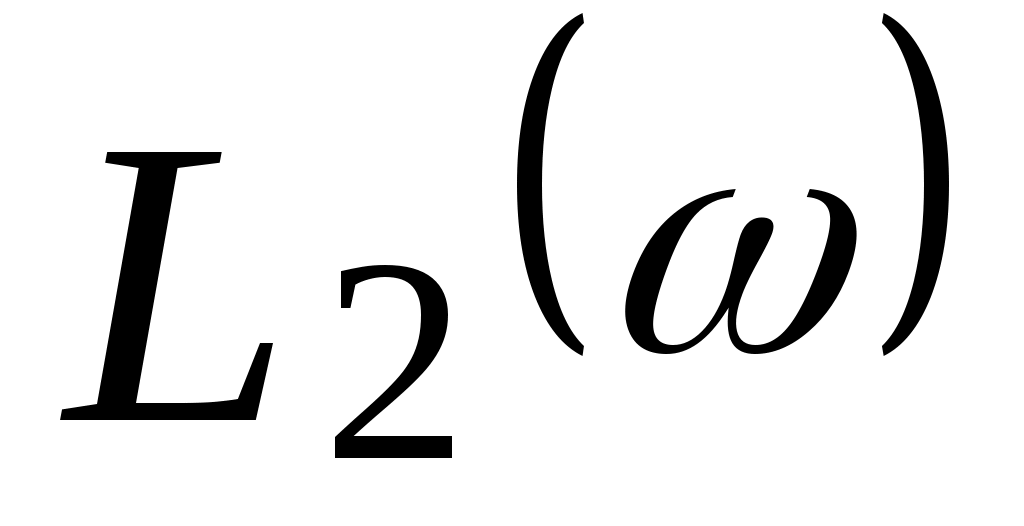 . Эта характеристика имеет следующие особенности: . Эта характеристика имеет следующие особенности:
наклон 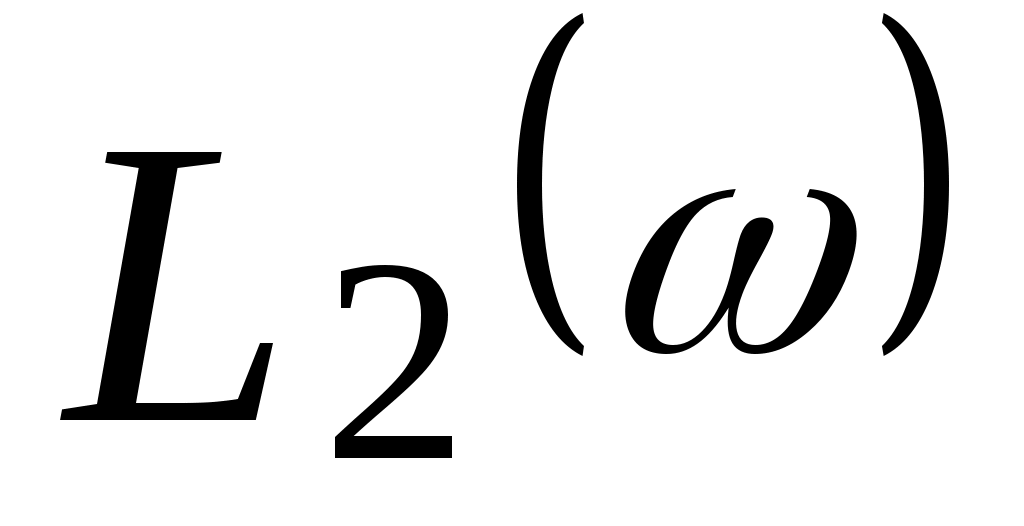 равен -20 дБ/дек во всем диапазоне частот, равен -20 дБ/дек во всем диапазоне частот,
н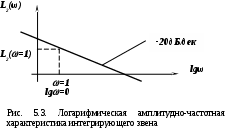
а частоте =1 значение 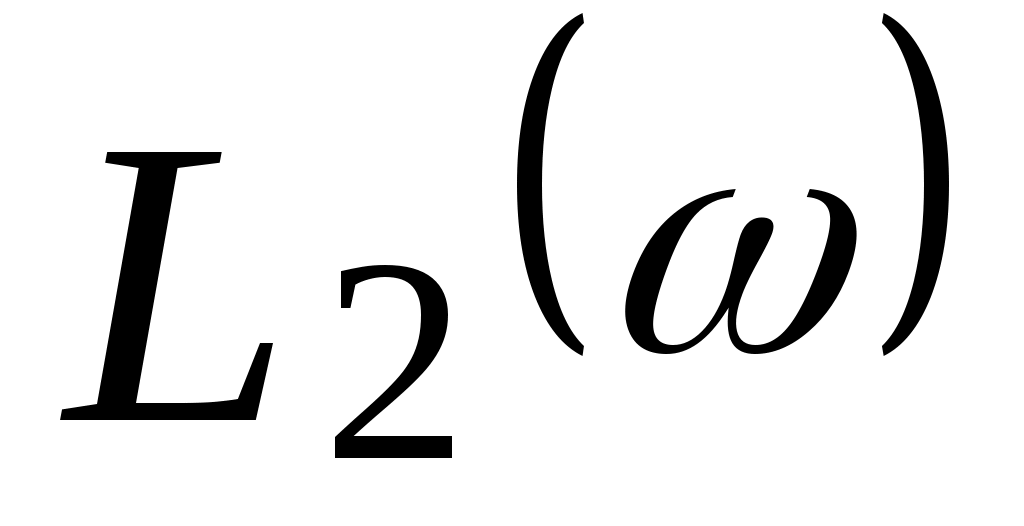 равно равно 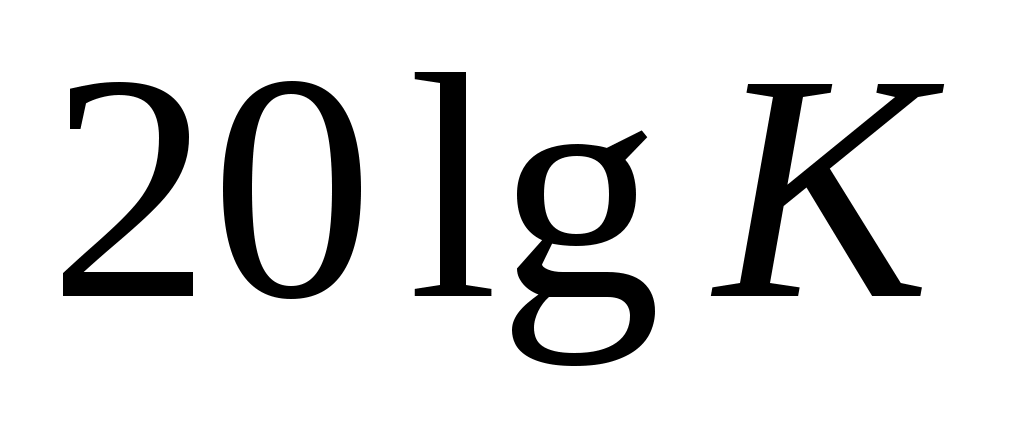 , т.е. , т.е. 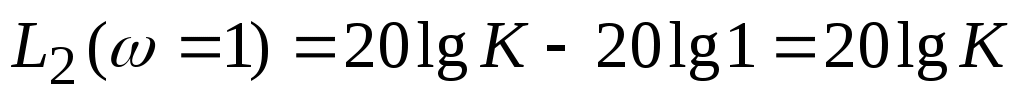 . .
Ф
азочастотная характеристика 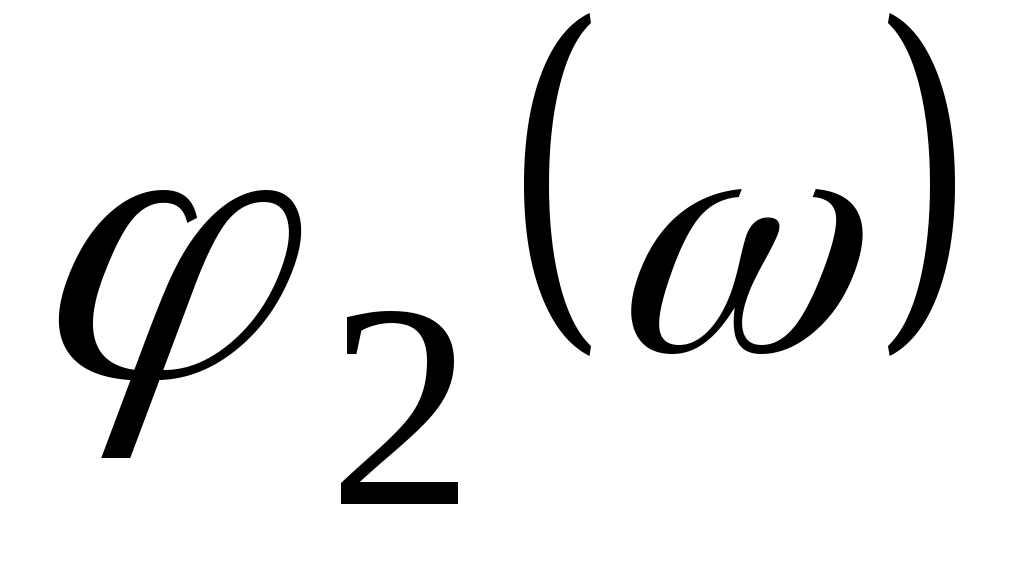 постоянна во всем диапазоне частот постоянна во всем диапазоне частот 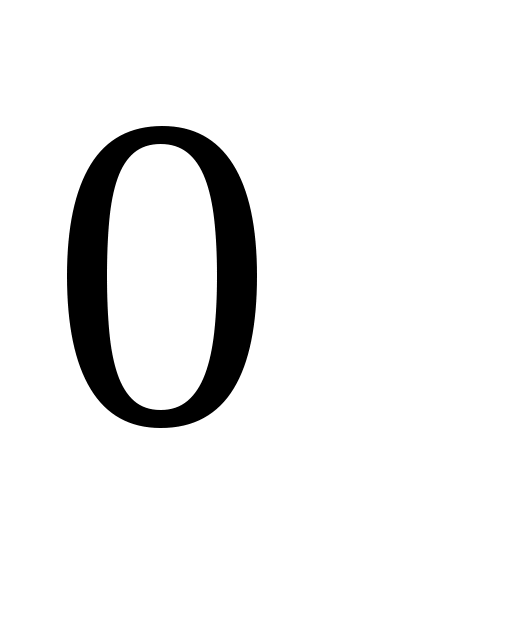 < < < <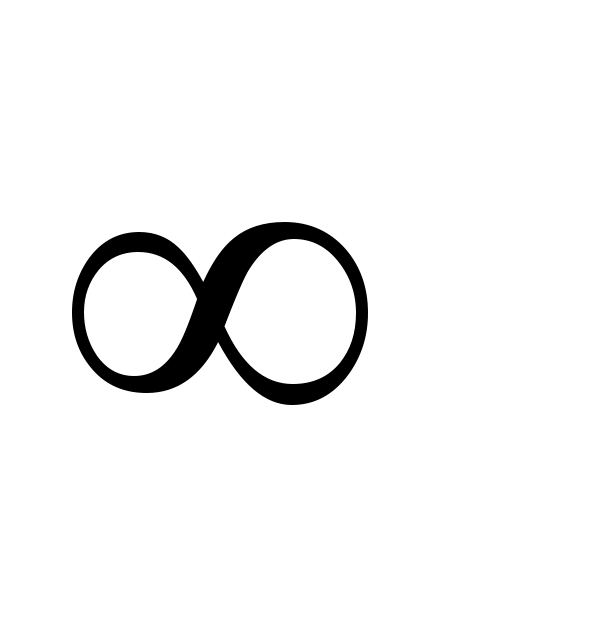 и равна и равна 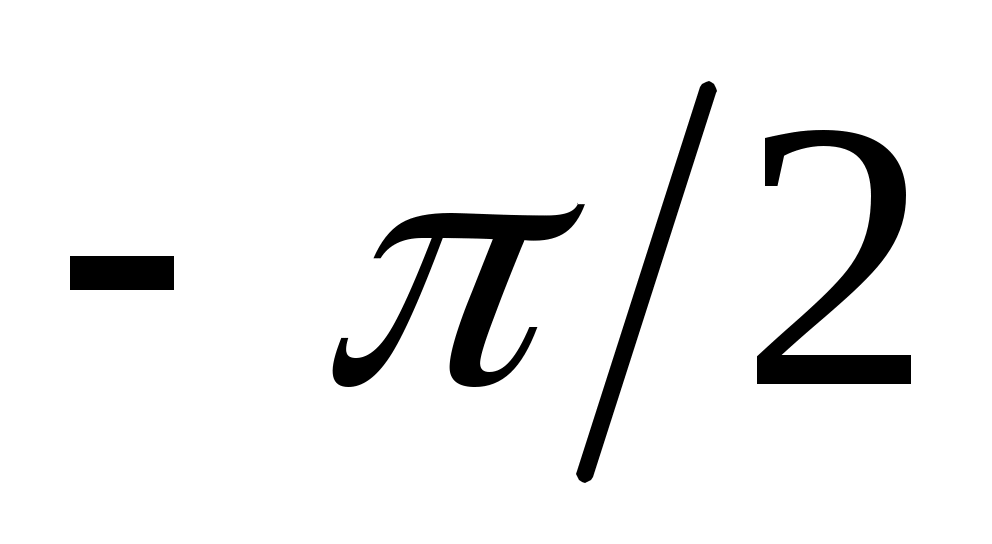 (рис.4.4.) (рис.4.4.)
Для оценки коэффициента 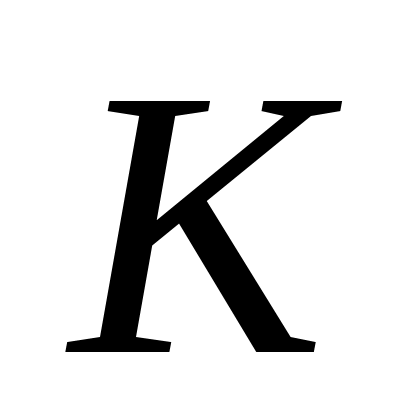 по по 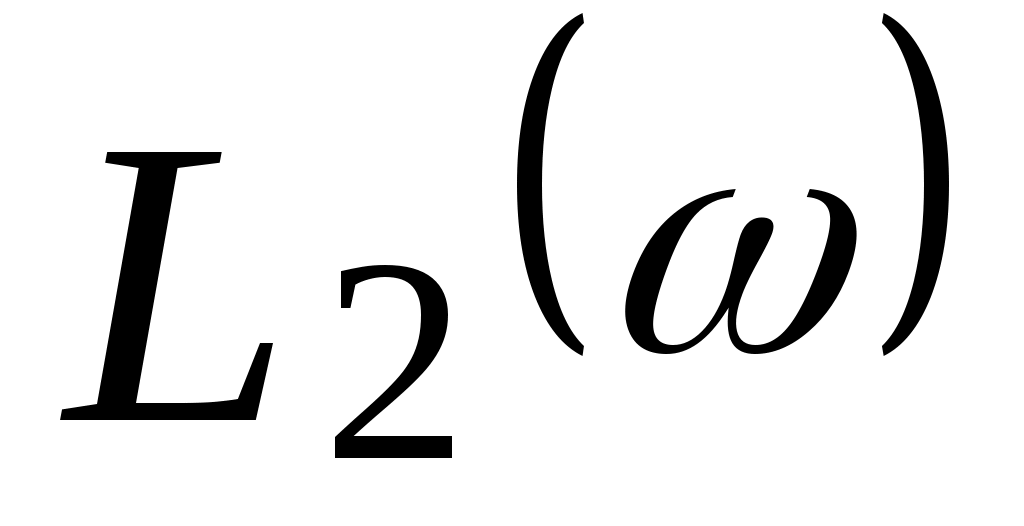 следует воспользоваться соотношением следует воспользоваться соотношением 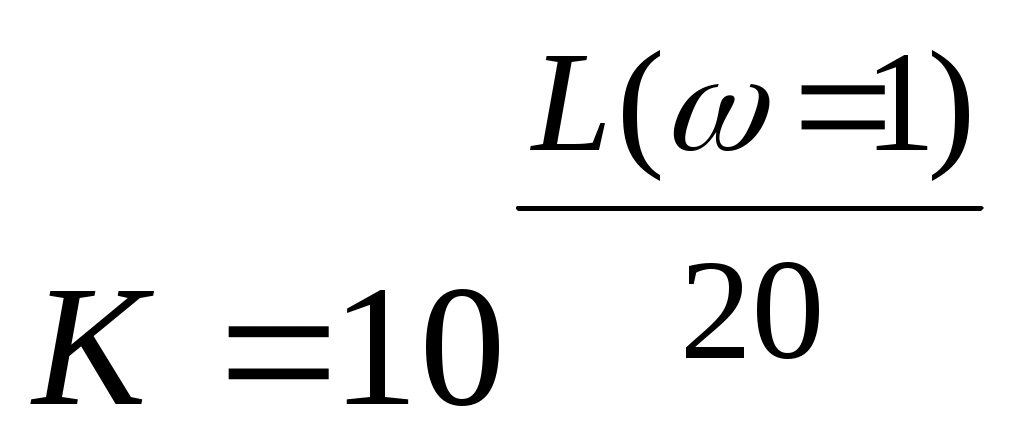 . .
Дифференцирующее звено
Уравнение работы дифференцирующего звена имеет следующий вид:
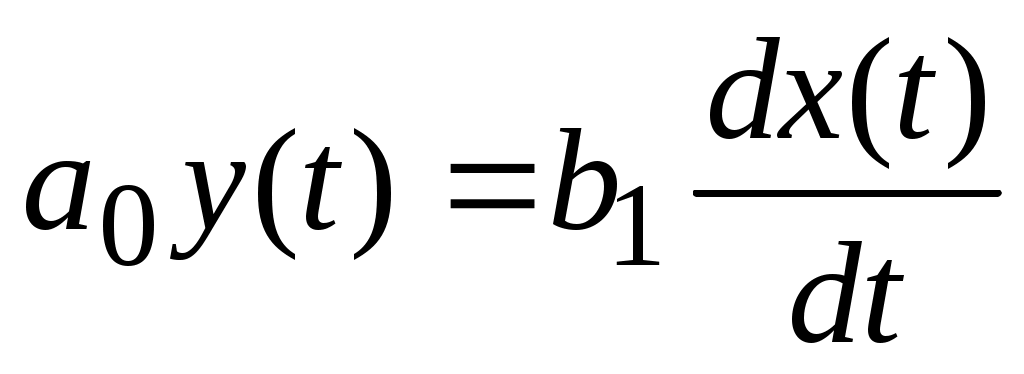 . .
Дифференцирующим звеном является конденсатор, ток в котором i(t) определяется соотношением 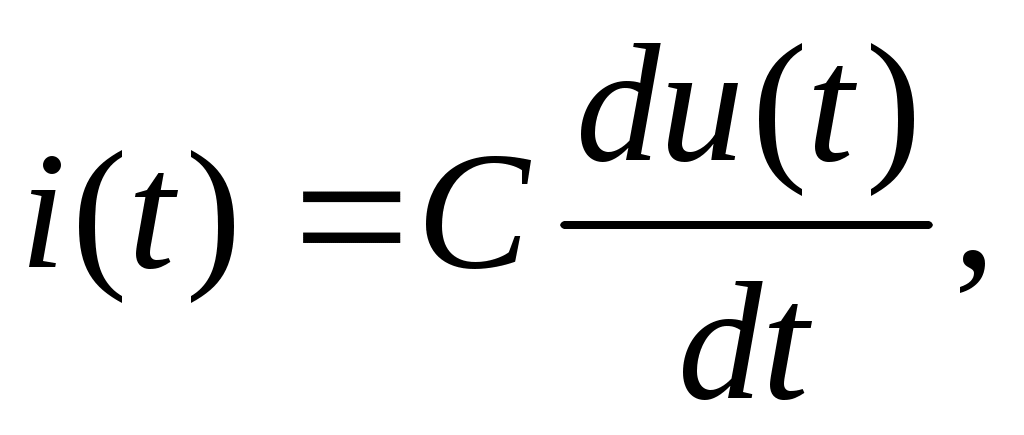 а также тахогенератор постоянного тока, вырабатывающий напряжение а также тахогенератор постоянного тока, вырабатывающий напряжение 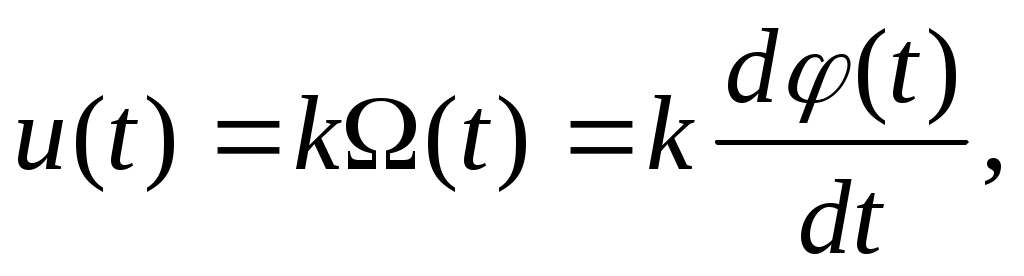 пропорциональное производной от угла поворота (t). пропорциональное производной от угла поворота (t).
Преобразуя уравнение динамики по Лапласу, получаем 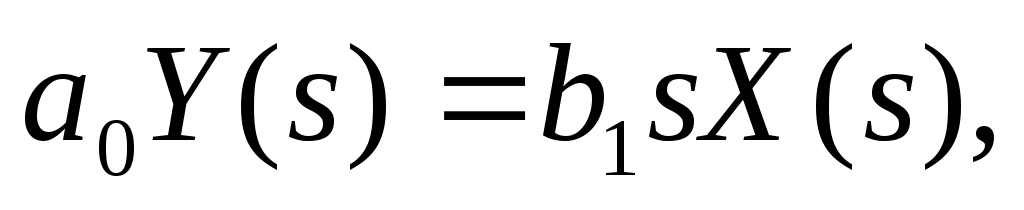 откуда найдем передаточную функцию звена: откуда найдем передаточную функцию звена:
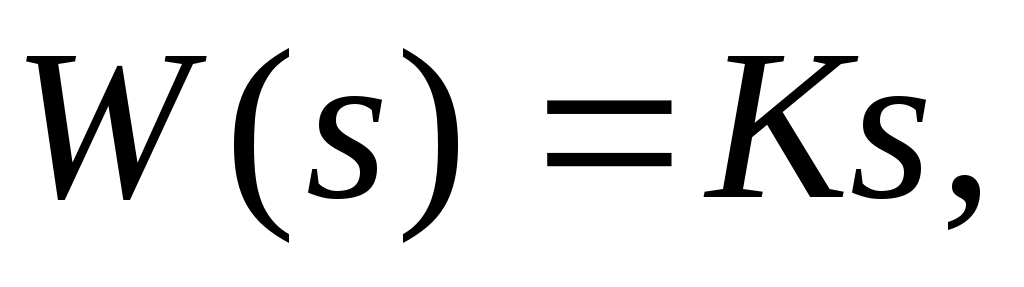
где 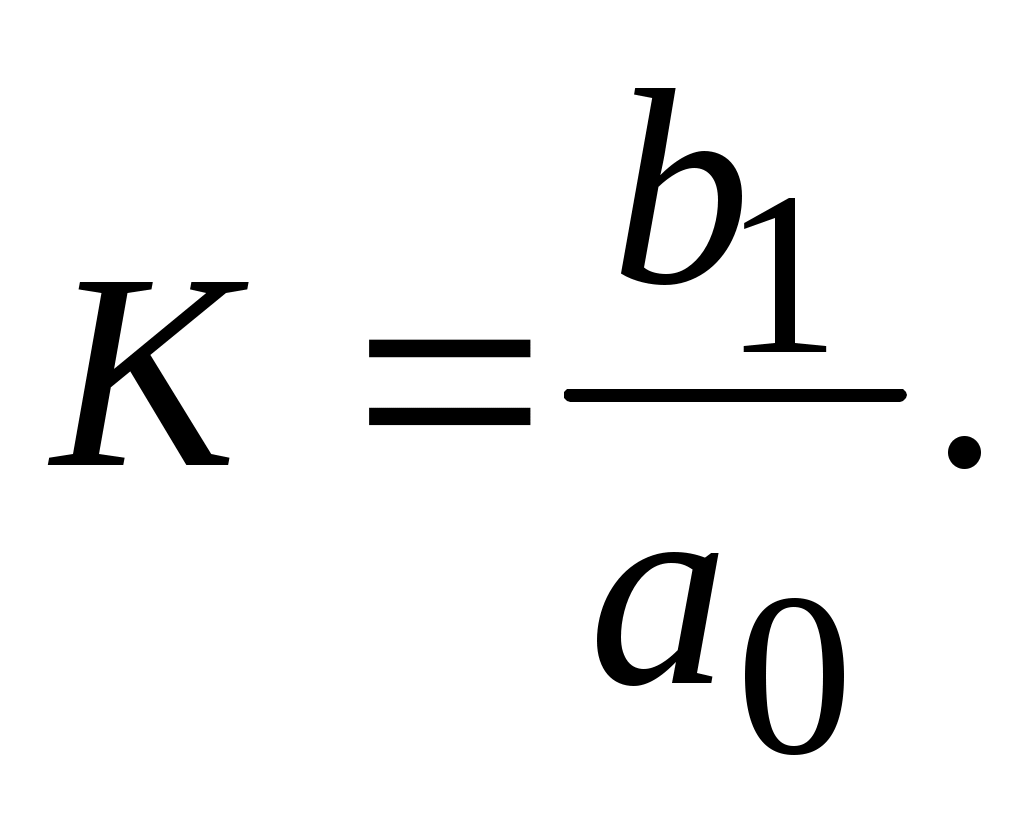
Итак, передаточная функция дифференцирующего звена равна
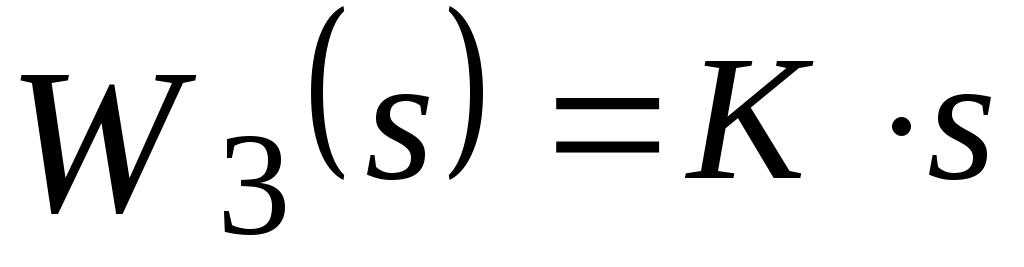 . .
Из передаточной функции дифференцирующего звена могут быть найдены все его частотные характеристики:
комплексный коэффициент передачи
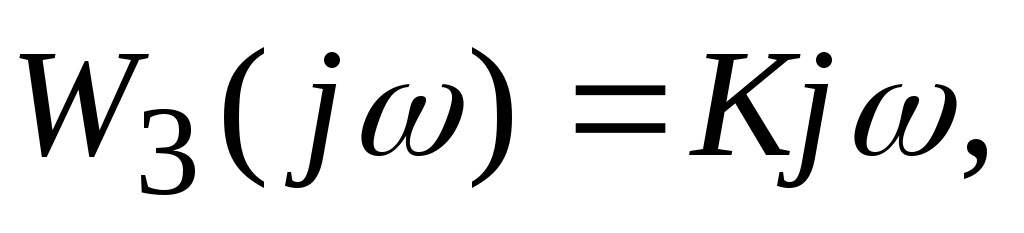
вещественная частотная характеристика
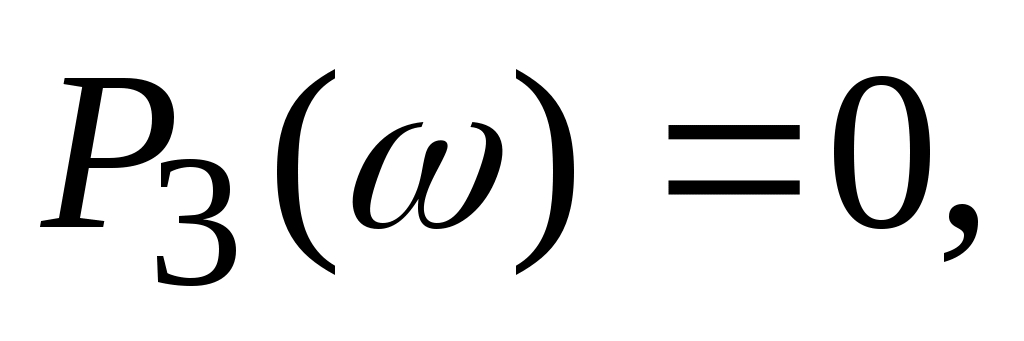
мнимая частотная характеристика
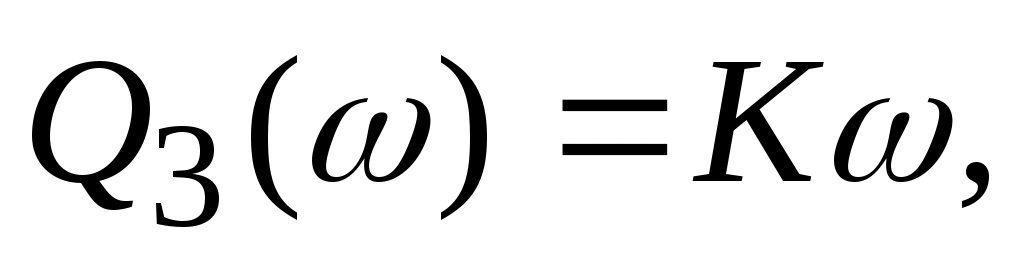
амплитудно-частотная характеристика
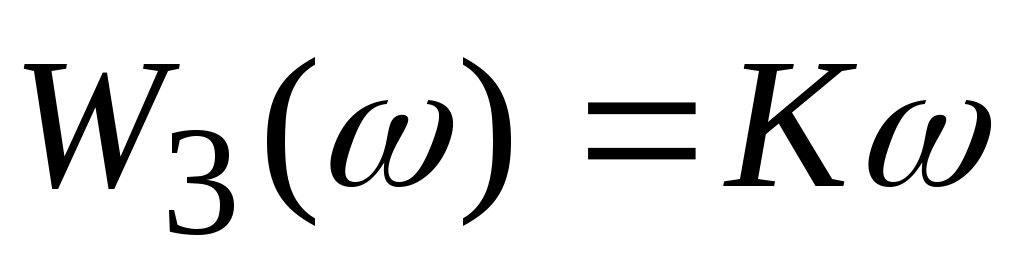
и фазовая частотная характеристика
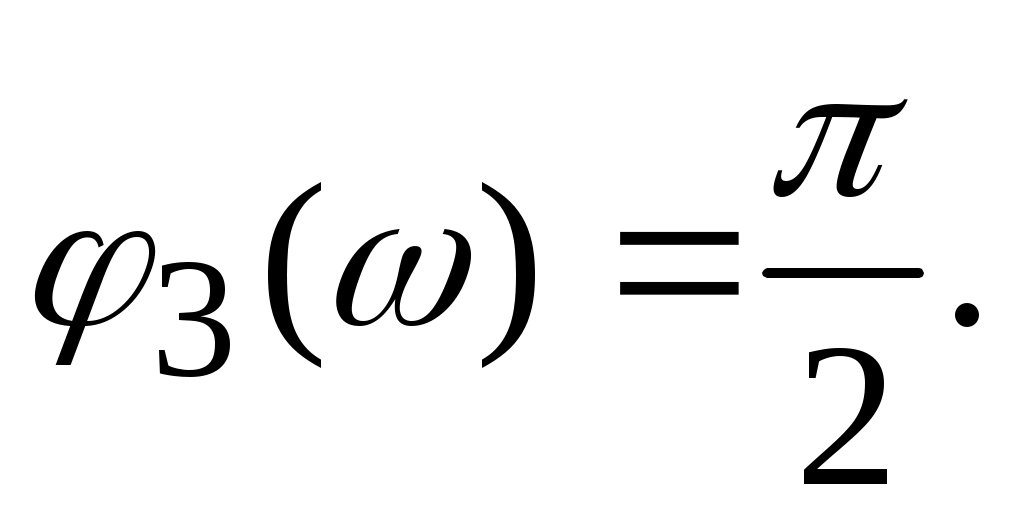
Годограф амплитудно-фазовой частотной характеристики (АФЧХ) дифференцирующего звена, зависимость Q() от P(), представляет собой прямую линию, совпадающую с положительным направлением мнимой оси (от 0 до  ). ).
Для нахождения действительной ЛАЧХ прологарифмируем амплитудно-частотную характеристику:
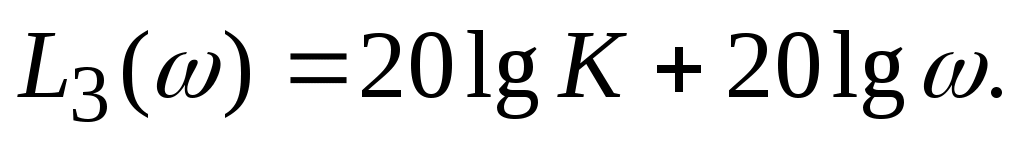
О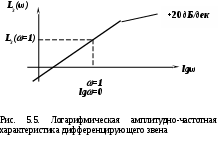
тсюда следует, что логарифмическая амплитудно-частотная характеристика дифференцирующего звена является прямой линией с наклоном +20 дБ/дек (рис.5.5).
Логарифмические частотные характеристики имеют следующие особенности.
Наклон 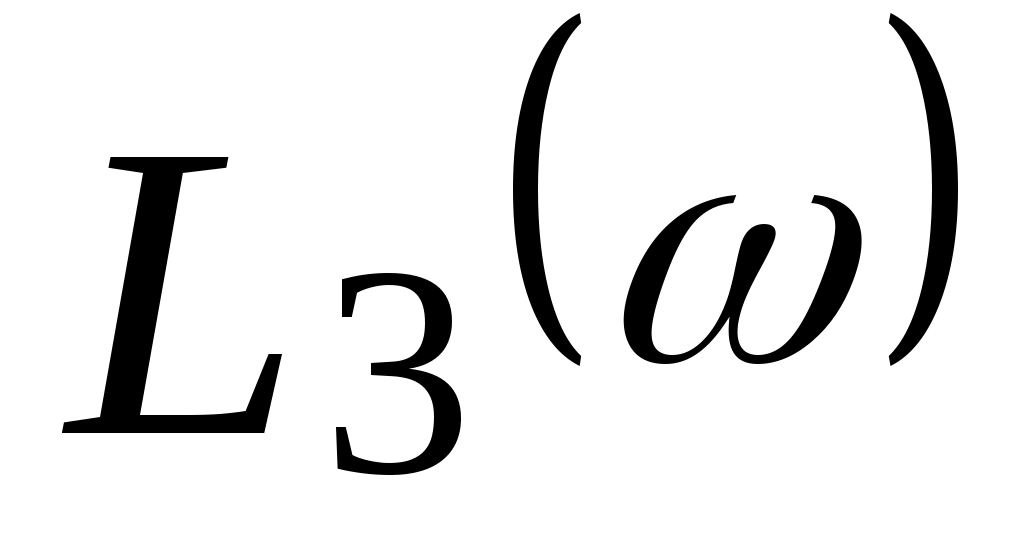 равен +20 дБ/дек во всем диапазоне частот равен +20 дБ/дек во всем диапазоне частот 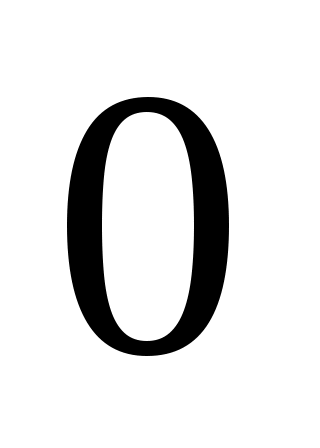 < < < <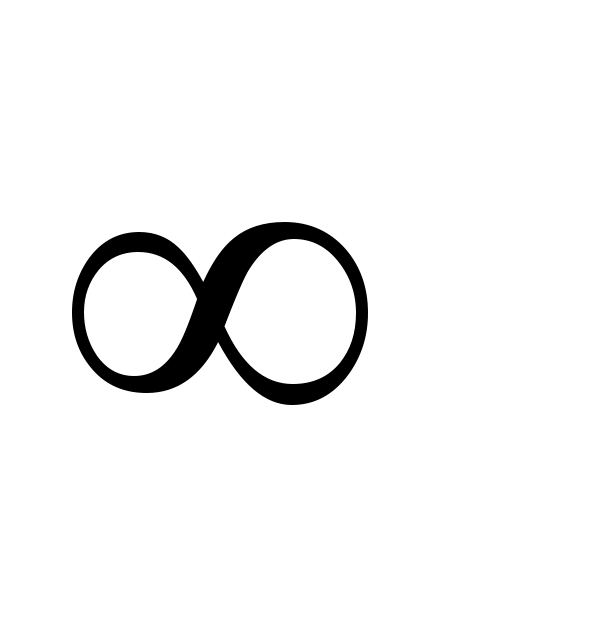 . .
на частоте 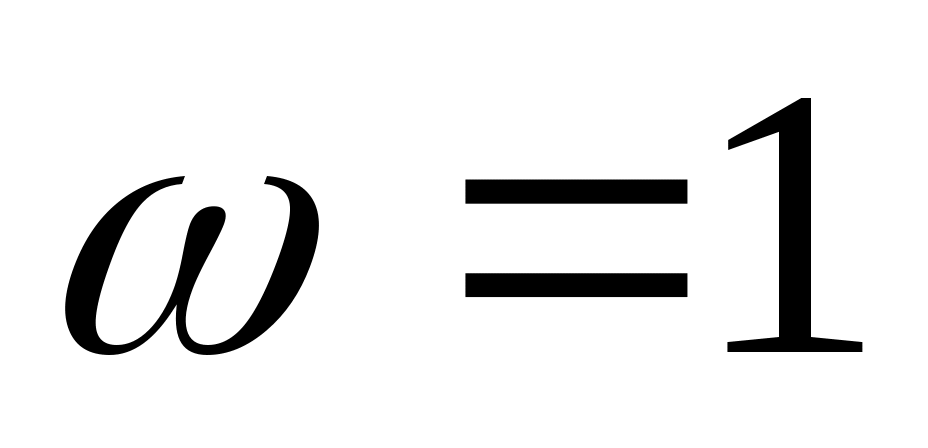 значение значение 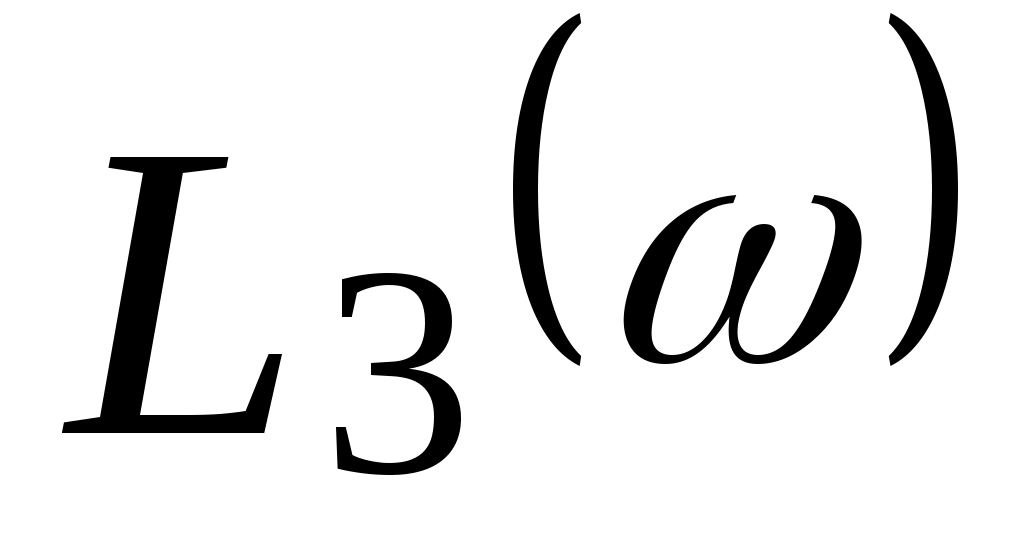 равно равно 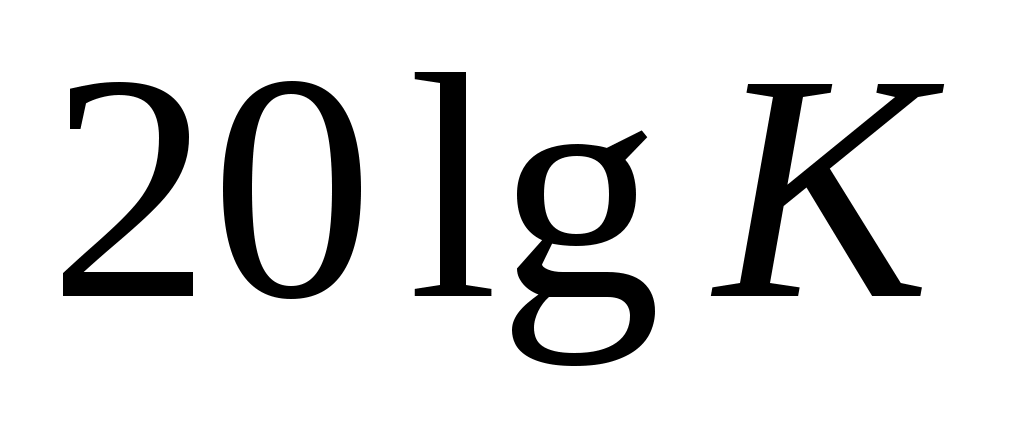 , т.е. , т.е. 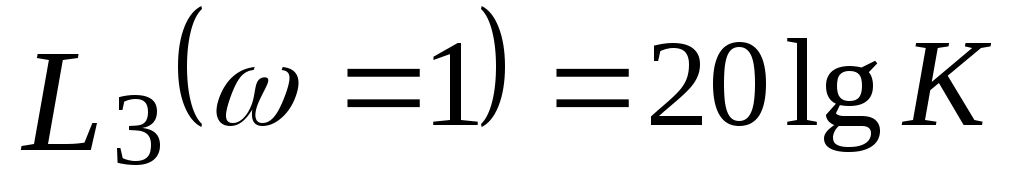
ф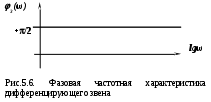
азочастотная характеристика 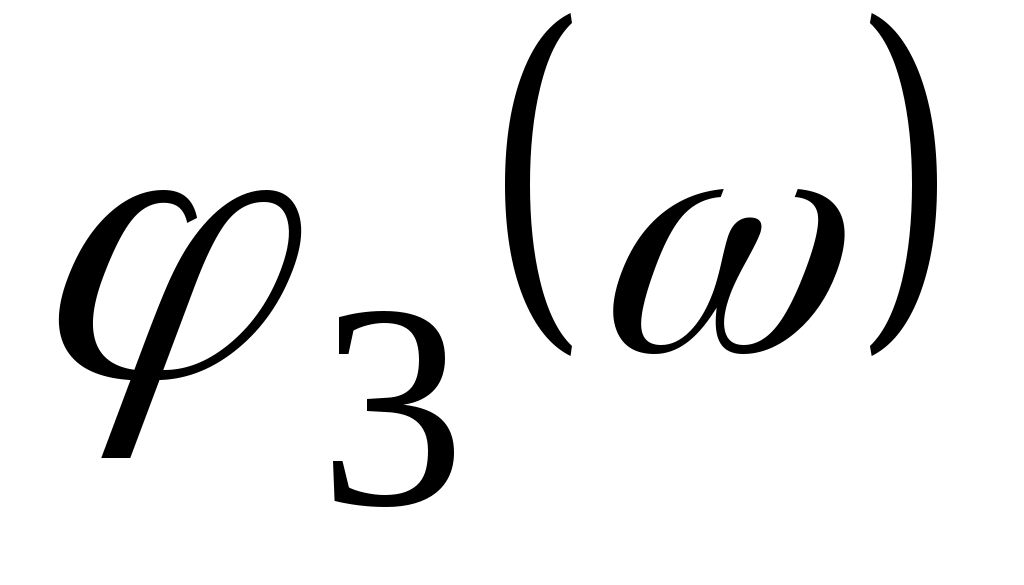 дифференцирующего звена постоянна во всем диапазоне частот дифференцирующего звена постоянна во всем диапазоне частот 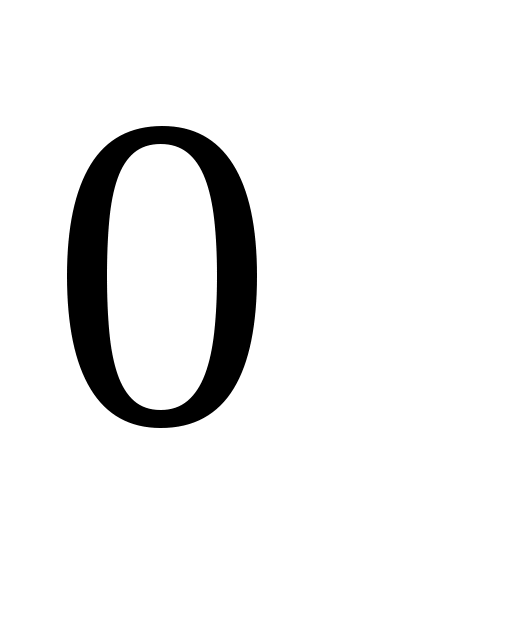 < < < <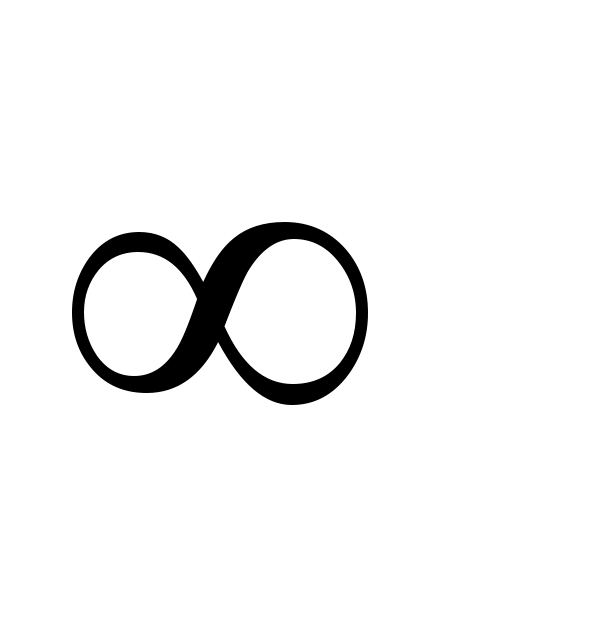 и равна и равна 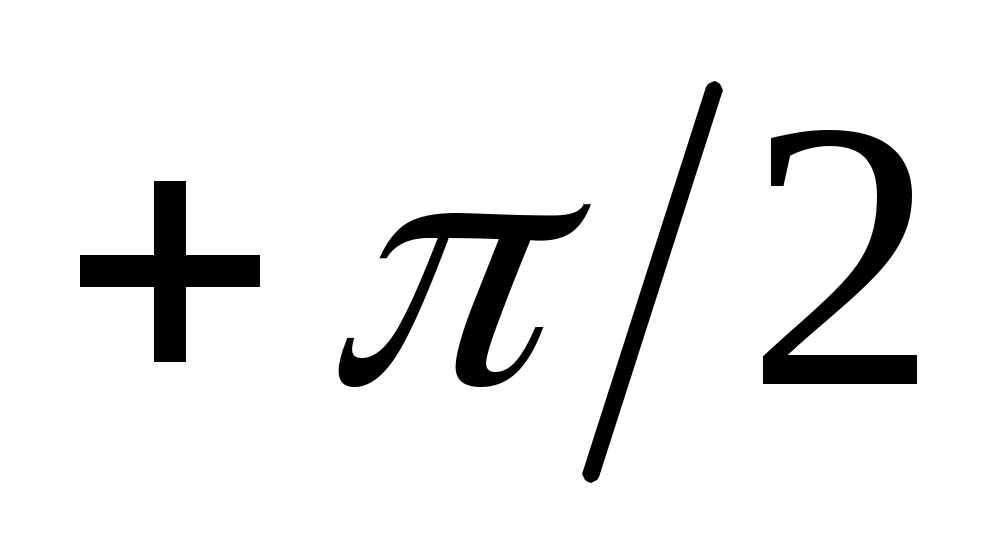 (рис.4.6.): (рис.4.6.):
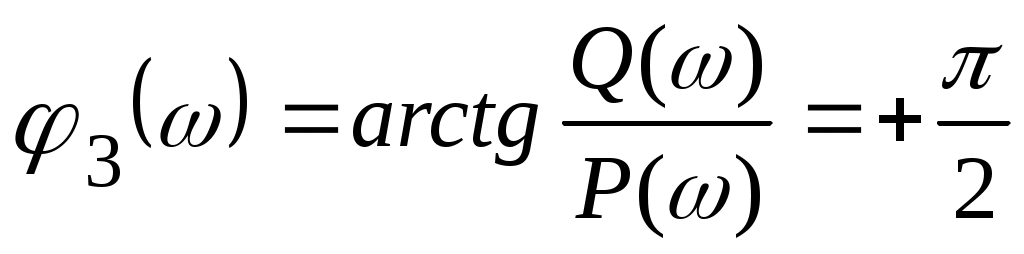 . .
Для оценки коэффициента пропорциональности 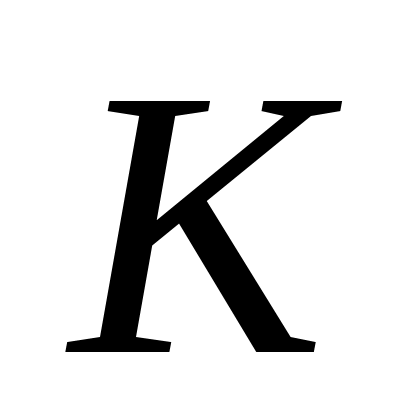 по логарифмической амплитудно-частотной характеристике по логарифмической амплитудно-частотной характеристике 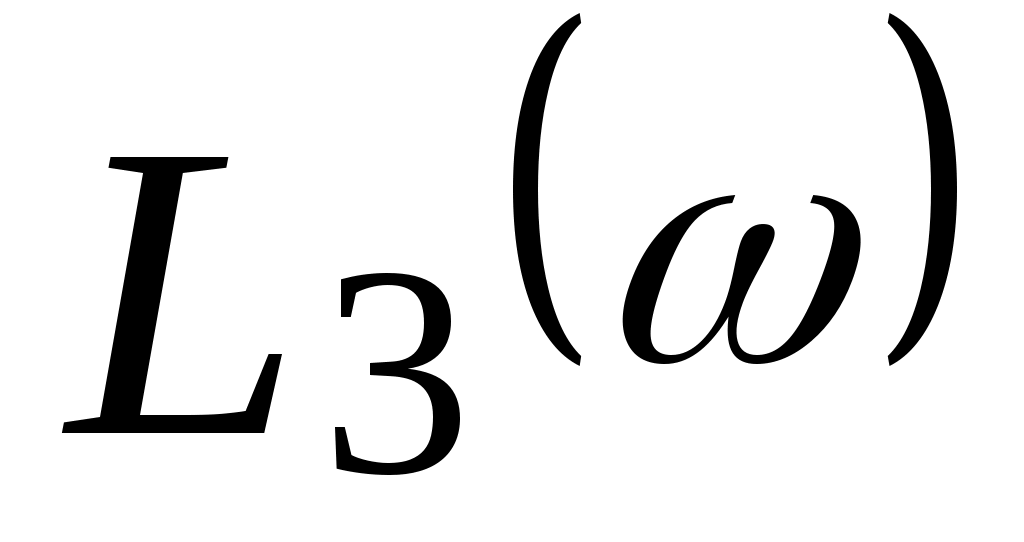 следует измерить значение следует измерить значение 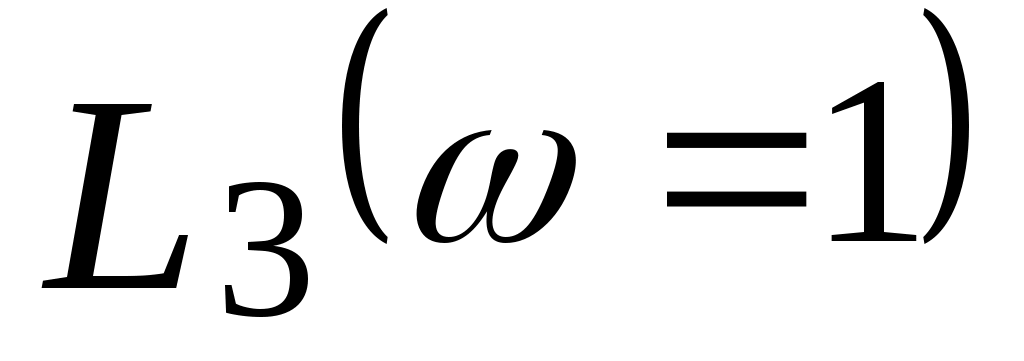 и воспользоваться соотношением и воспользоваться соотношением 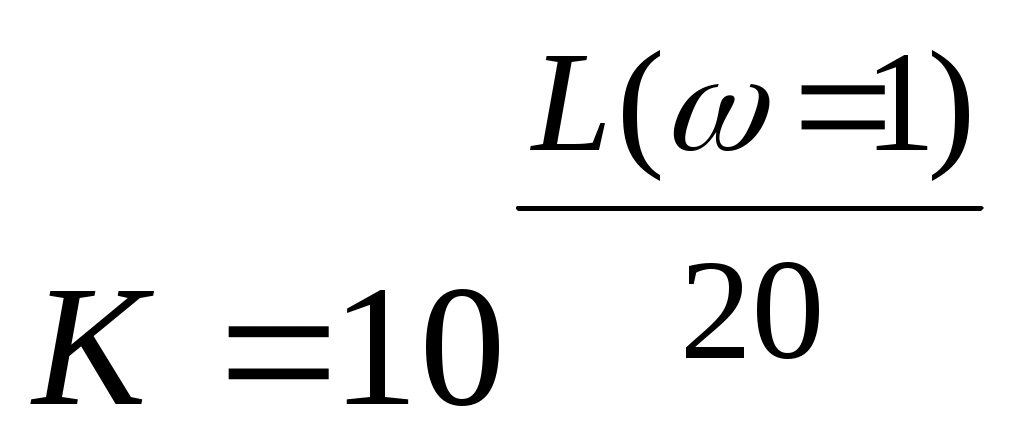 . .
Инерционное (апериодическое) звено первого порядка
Передаточная функция инерционного звена равна
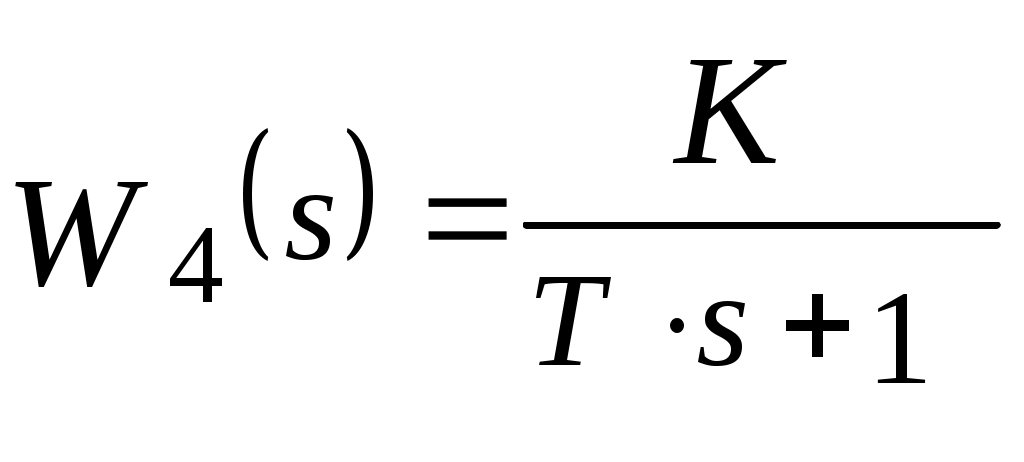 . .
Комплексный коэффициент передачи звена будет:
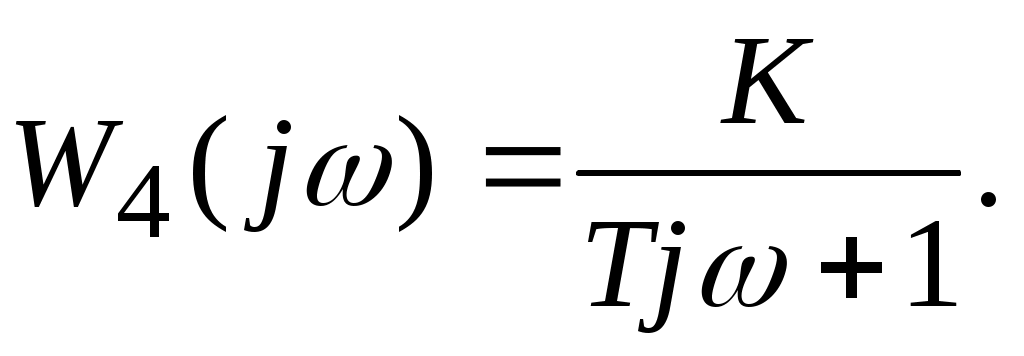
Для нахождения вещественной и мнимой частотных характеристик инерционного звена представим это выражение в следующем виде: 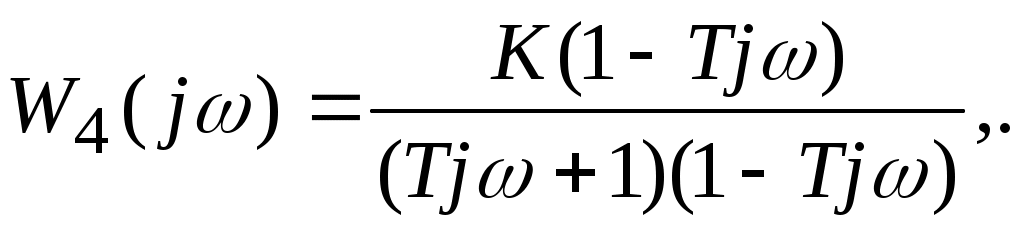 отсюда получим вещественную и мнимую частотные характеристики инерционного звена отсюда получим вещественную и мнимую частотные характеристики инерционного звена 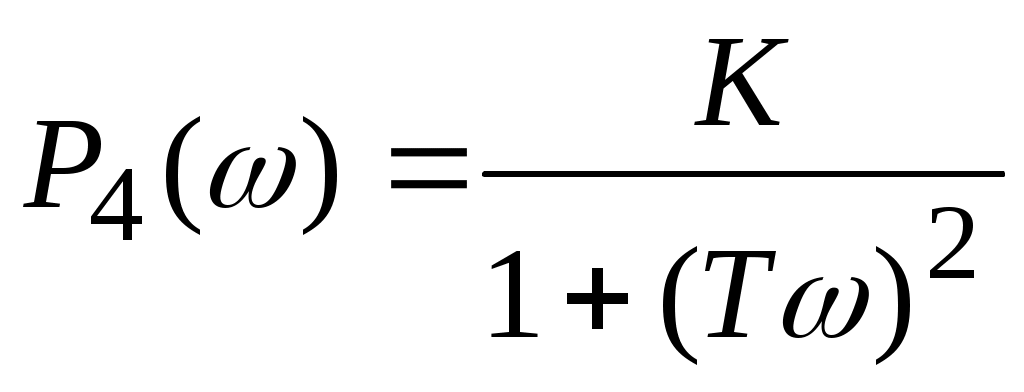 , , 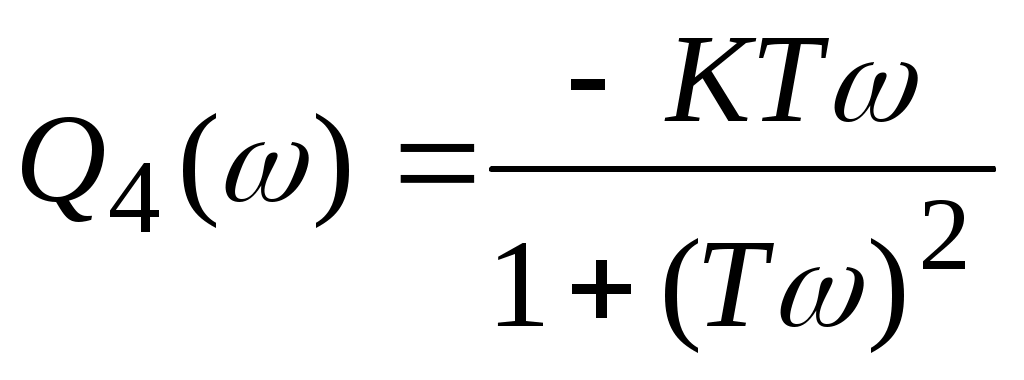 . Из полученных зависимостей следует, что функция . Из полученных зависимостей следует, что функция 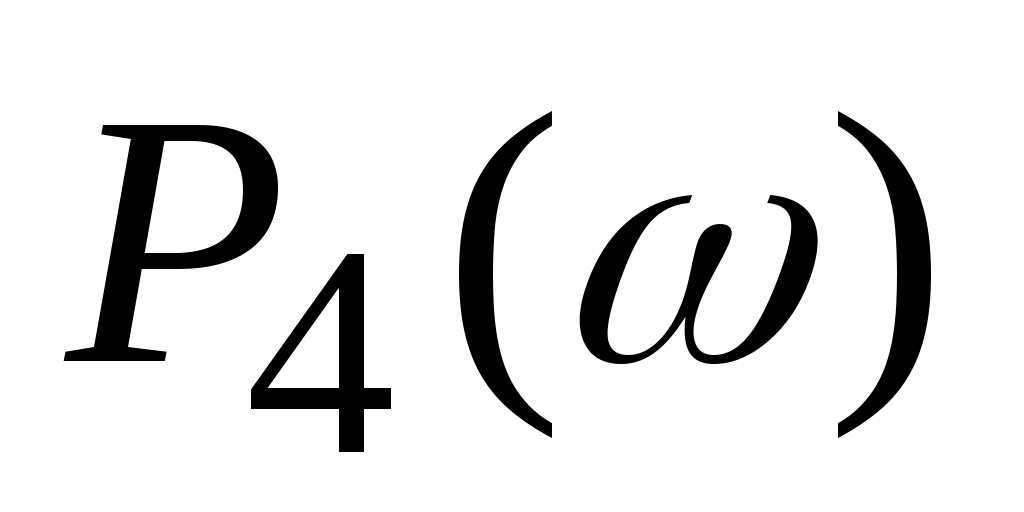 - четная, а функция - четная, а функция 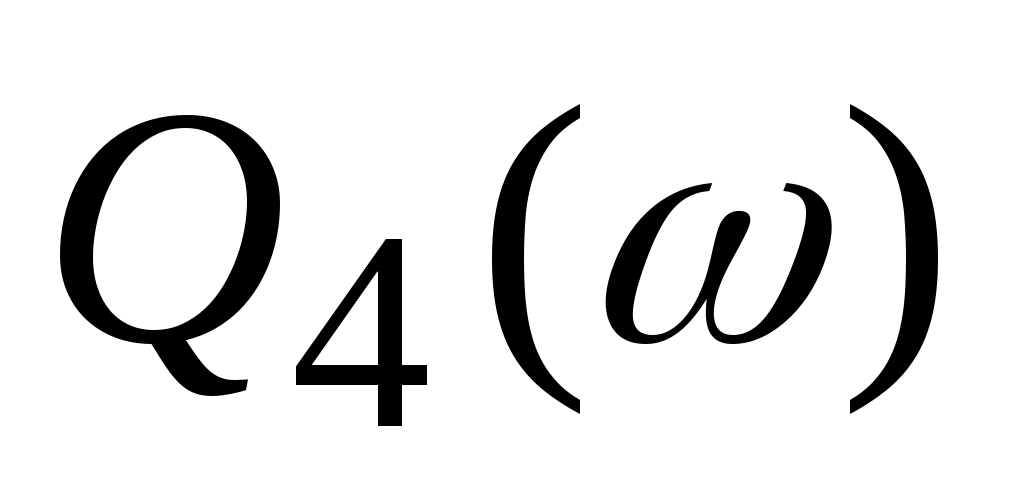 - нечетная. - нечетная.
Для нахождения годографа АФЧХ инерционного звена, зависимости Q4() от P4(), найдем уравнение в функции от переменных 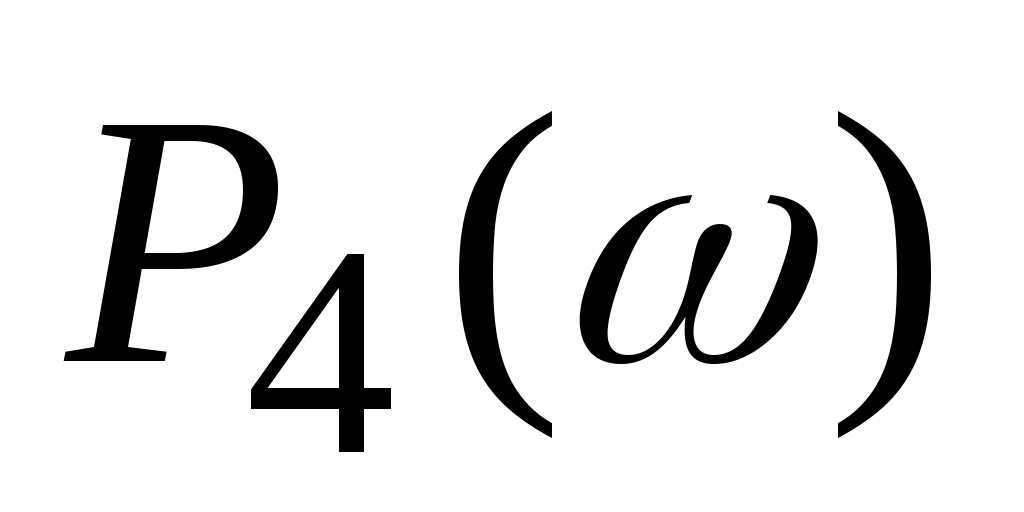 и и 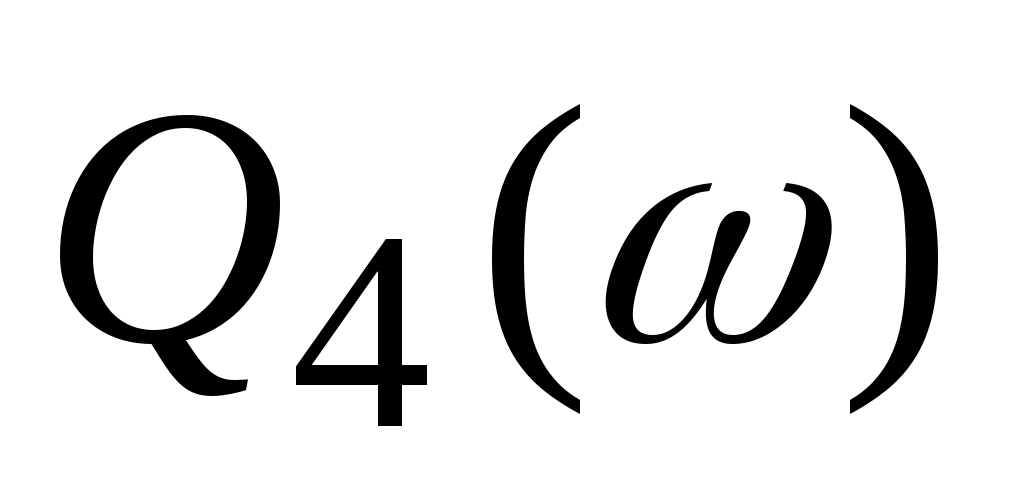 . .
Получим 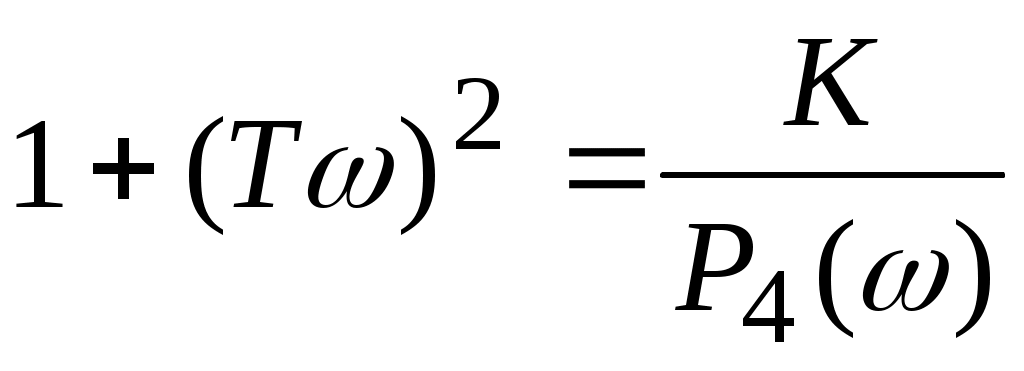 . Подставляя это выражение в формулу для Q4(), находим: . Подставляя это выражение в формулу для Q4(), находим: 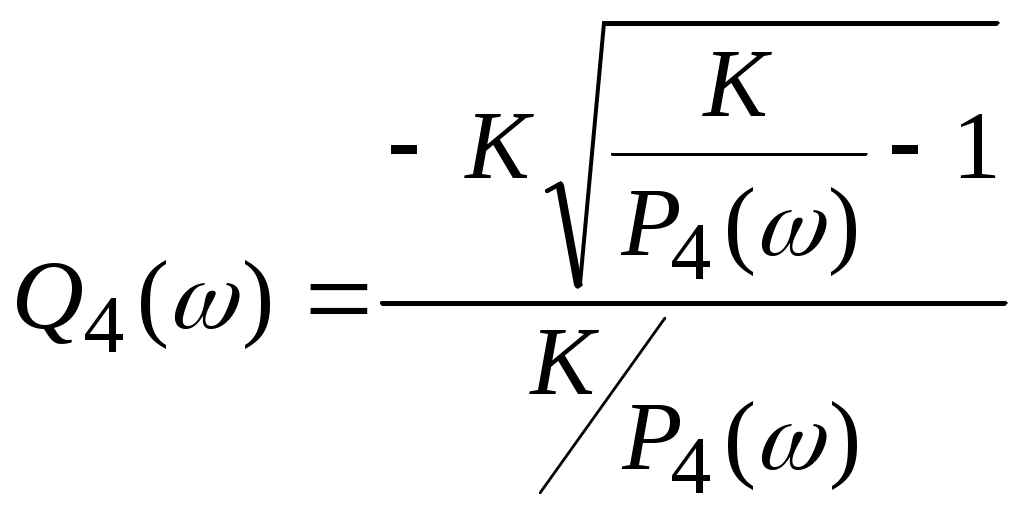 . Преобразуя эту зависимость, имеем: . Преобразуя эту зависимость, имеем: 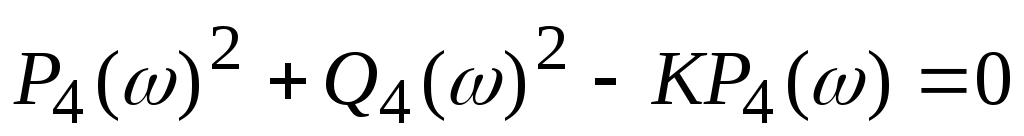 . Таким образом, годограф амплитудно-фазовой частотной характеристики (АФЧХ) инерционного звена представляет собой окружность . Таким образом, годограф амплитудно-фазовой частотной характеристики (АФЧХ) инерционного звена представляет собой окружность
Учитывая известную связь между частотными характеристиками найдем амплитудно-частотную и фазовую частотные характеристики:
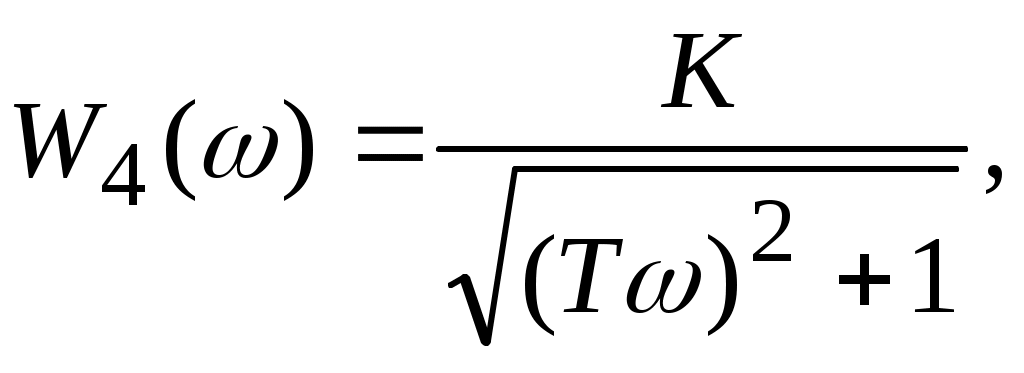
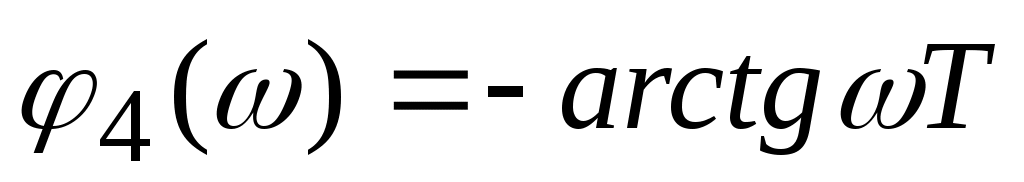 . .
Действительная логарифмическая амплитудная частотная характеристика равна
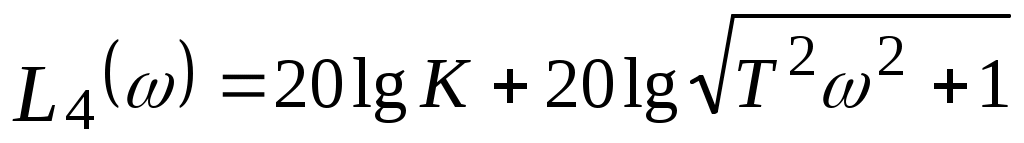
Характеристика 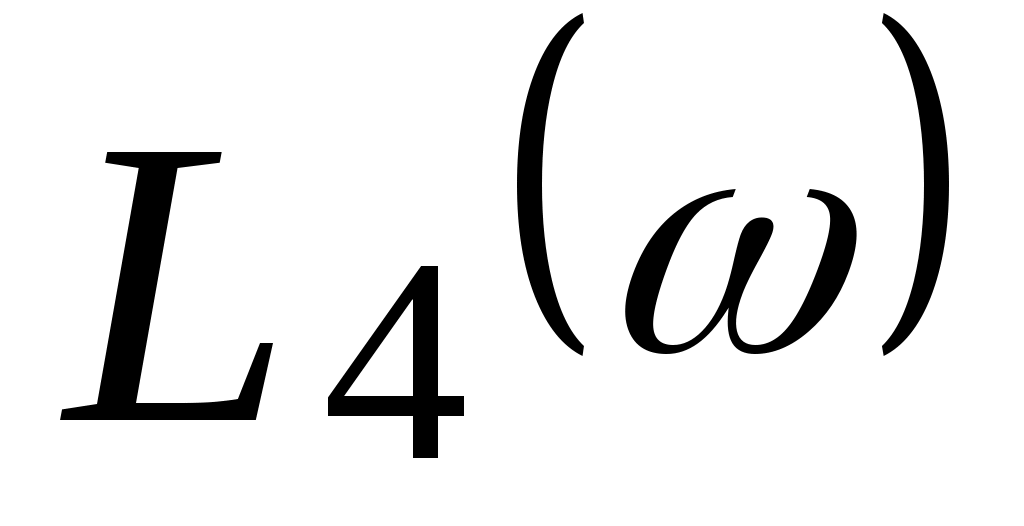 имеет низкочастотную имеет низкочастотную 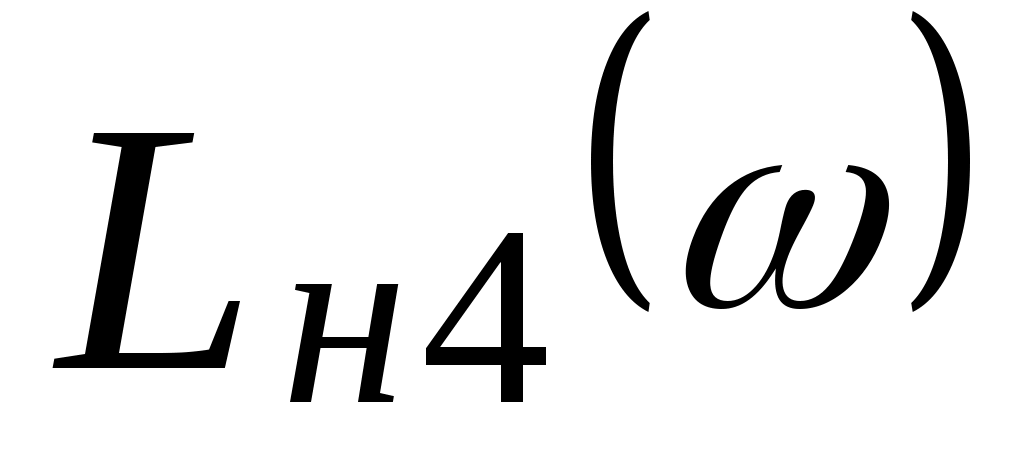 и высокочастотную и высокочастотную 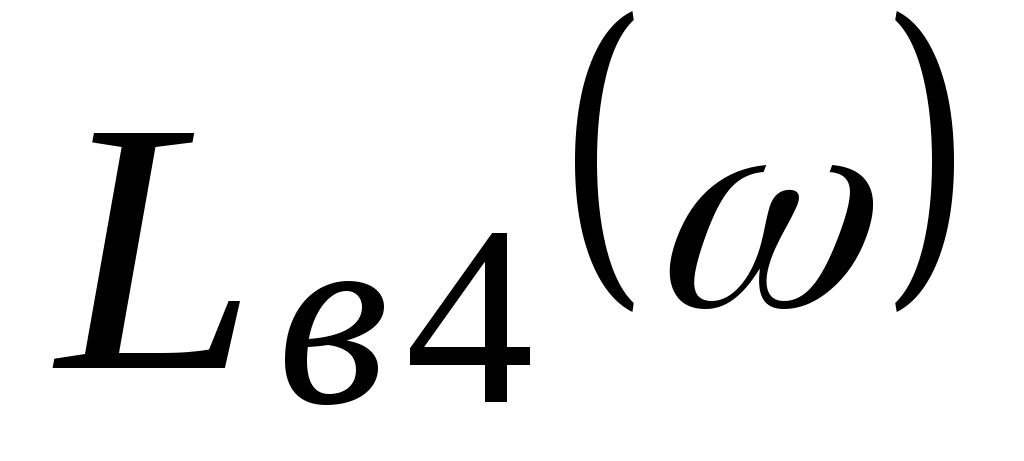 асимптоты, которые сопрягаются на частоте сопряжения асимптоты, которые сопрягаются на частоте сопряжения 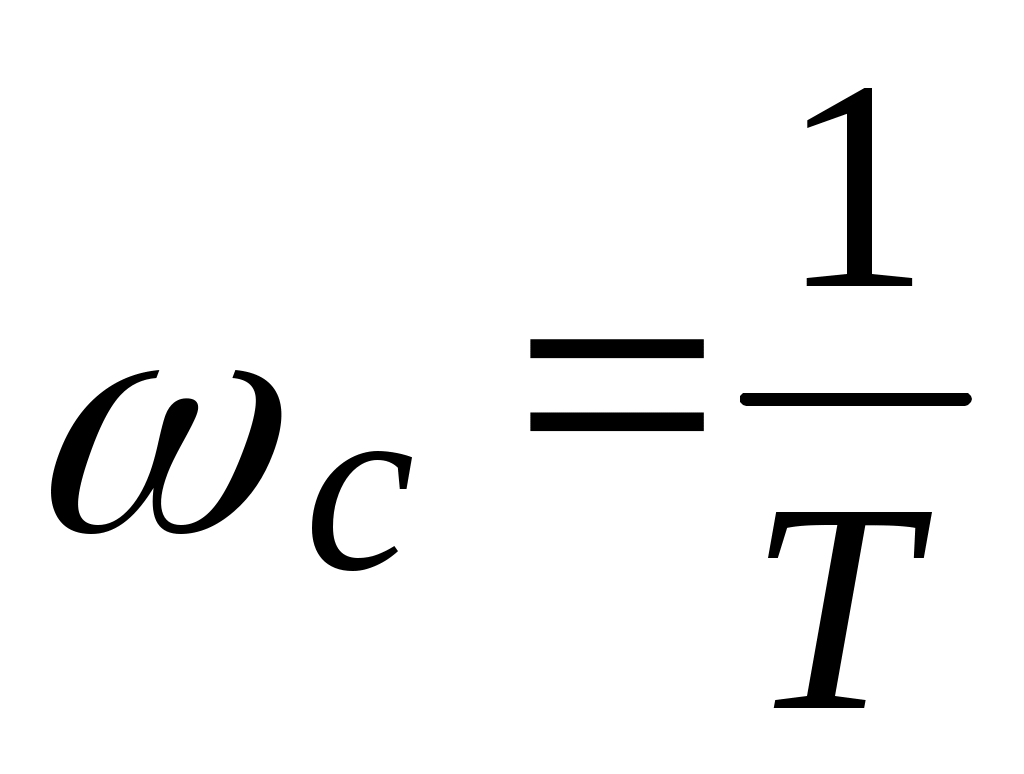 . .
Низкочастотная асимптота ЛАЧХ инерционного звена представляет собой предел, при этом 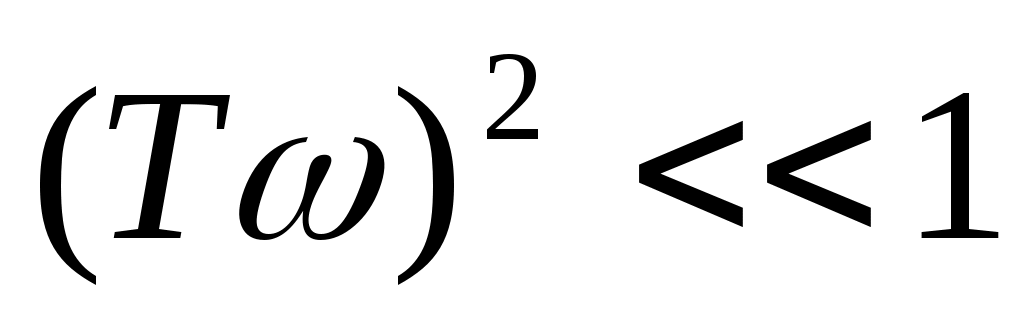 и второе слагаемое ЛАЧХ равно нулю. и второе слагаемое ЛАЧХ равно нулю.
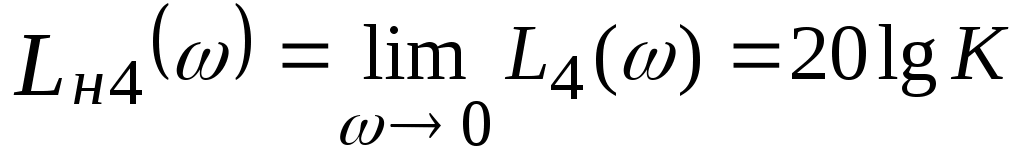
Высокочастотная асимптота ЛАЧХ находится как из условия 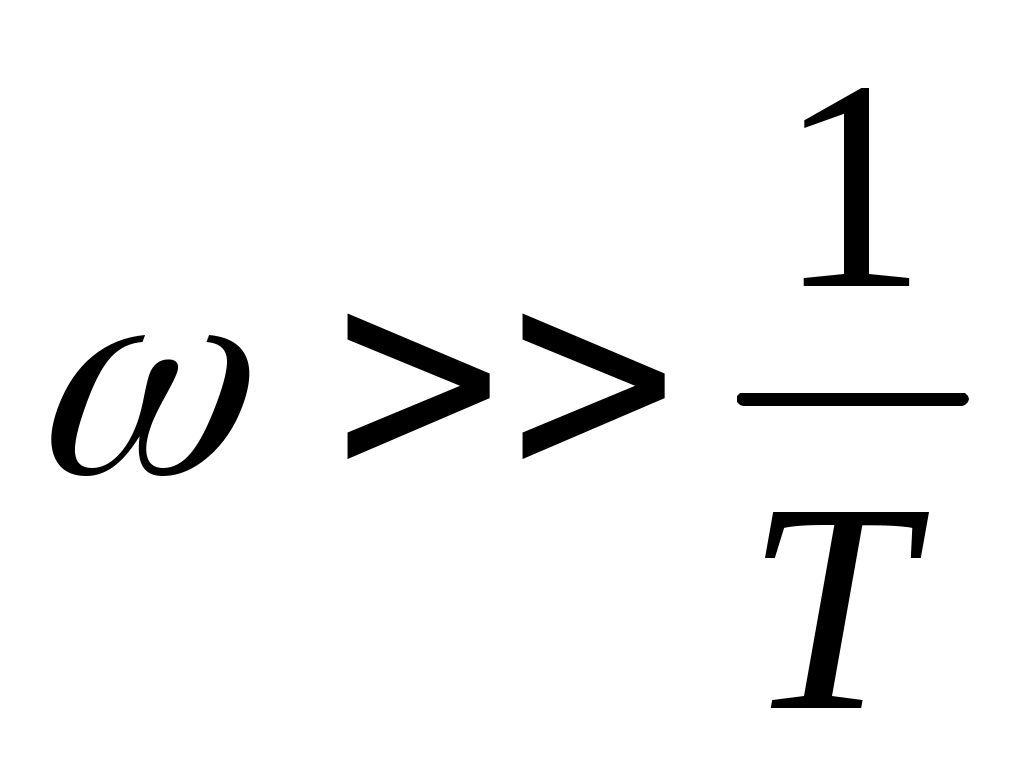 . Тогда . Тогда 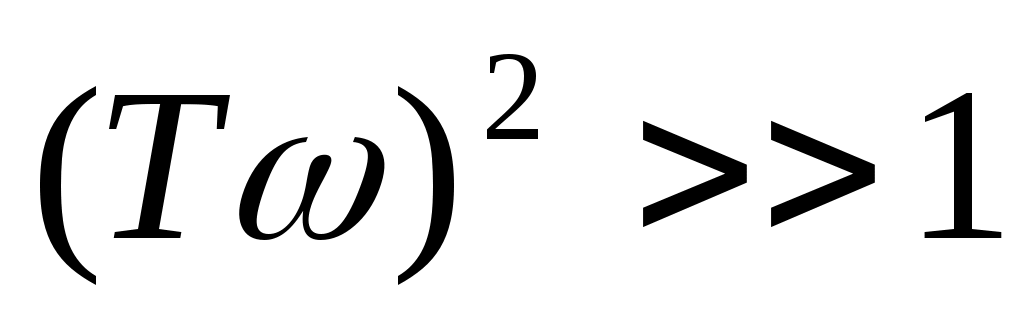 и и
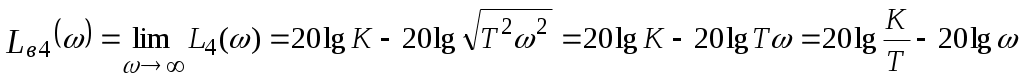 . .
Асимптотической ЛАЧХ является характеристика, составленная из асимптот - двух прямых линий: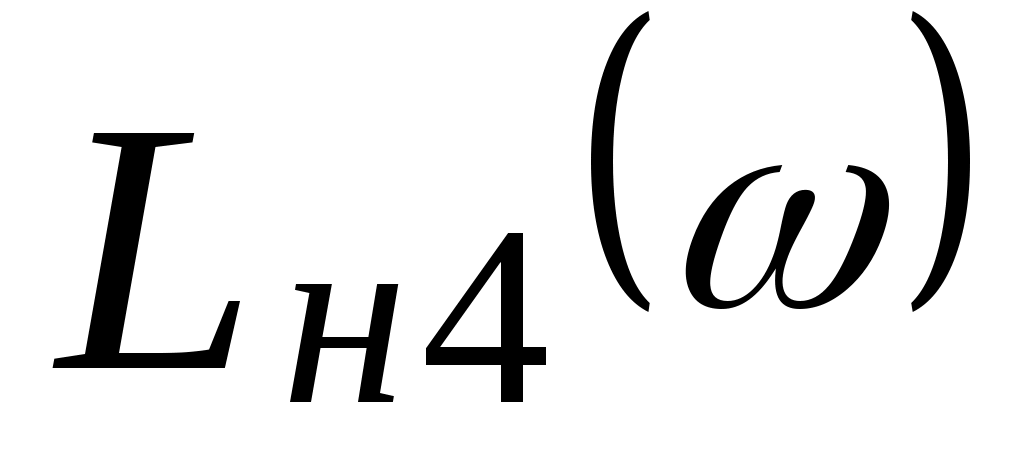 и и 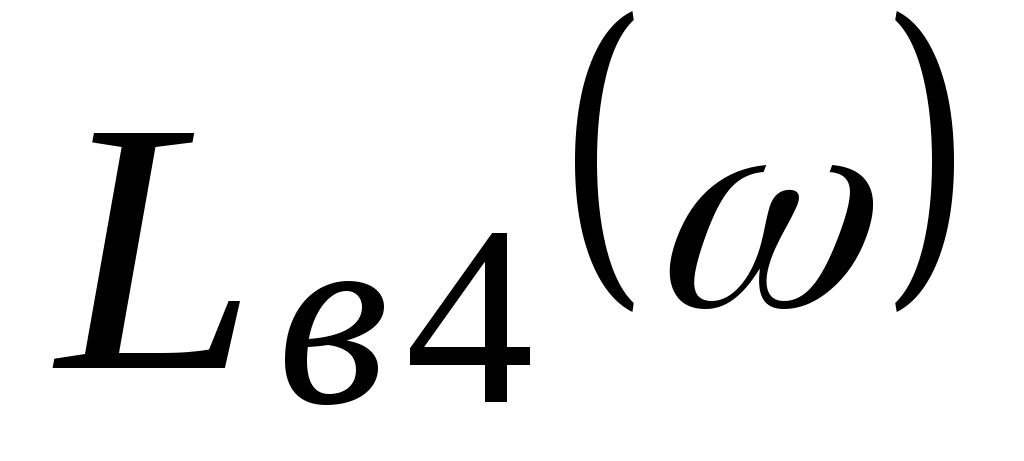
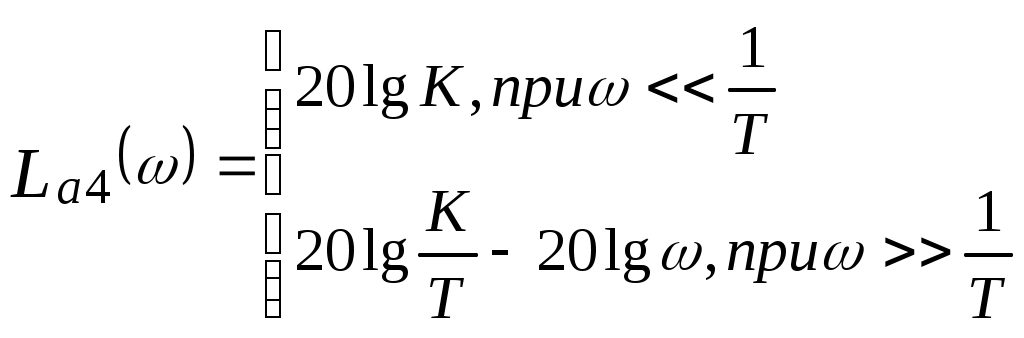
Графики 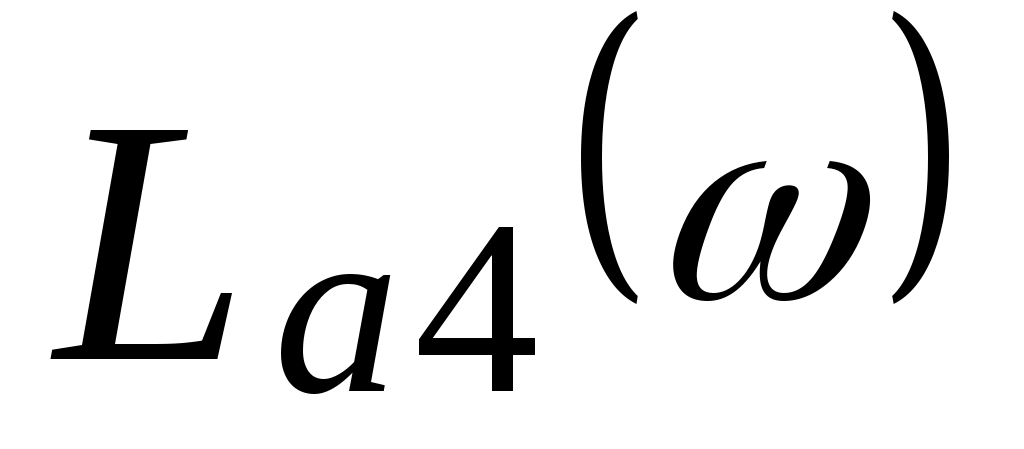 и показаны на рис. 5.7. и показаны на рис. 5.7.
Эти характеристики имеют следующие особенности:
низкочастотная асимптота 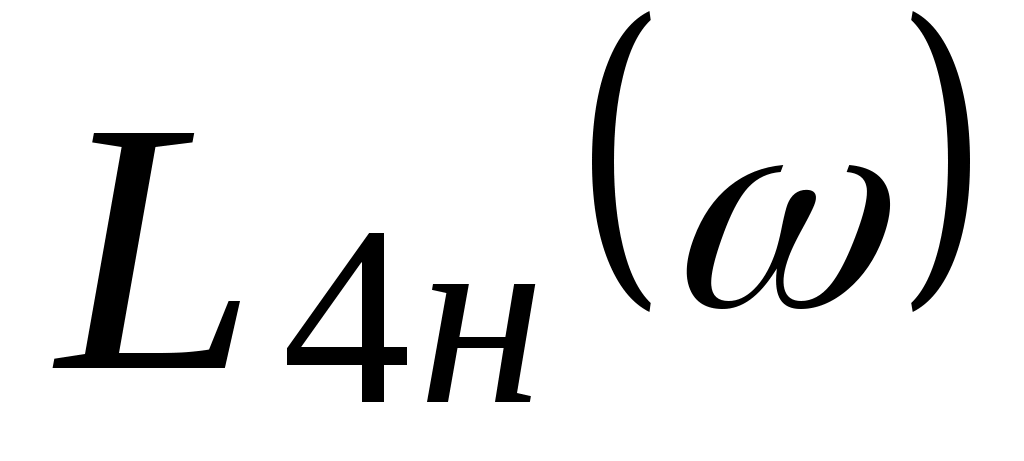 имеет 0 наклон, имеет 0 наклон,
высокочастотная асимптота 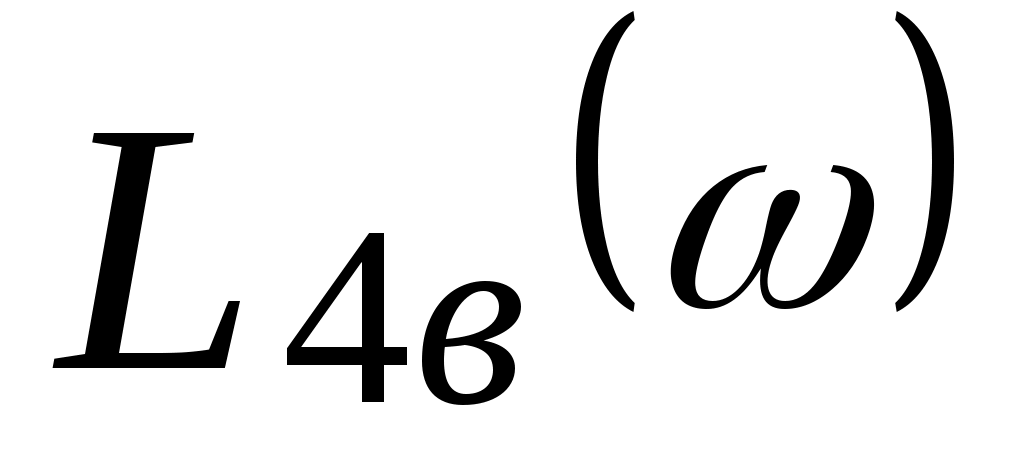 имеет наклон–20 дБ/дек, имеет наклон–20 дБ/дек,
асимптоты и сопрягаются на частоте сопряжения 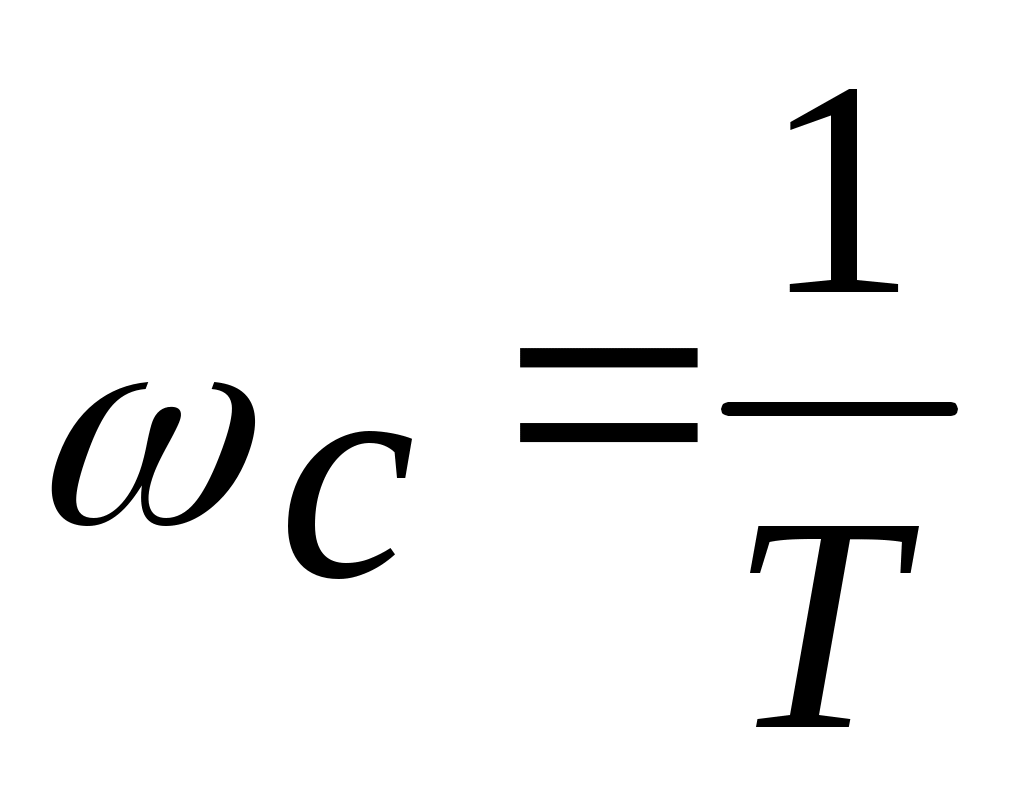 . .
фазочастотная характеристика на частоте сопряжения 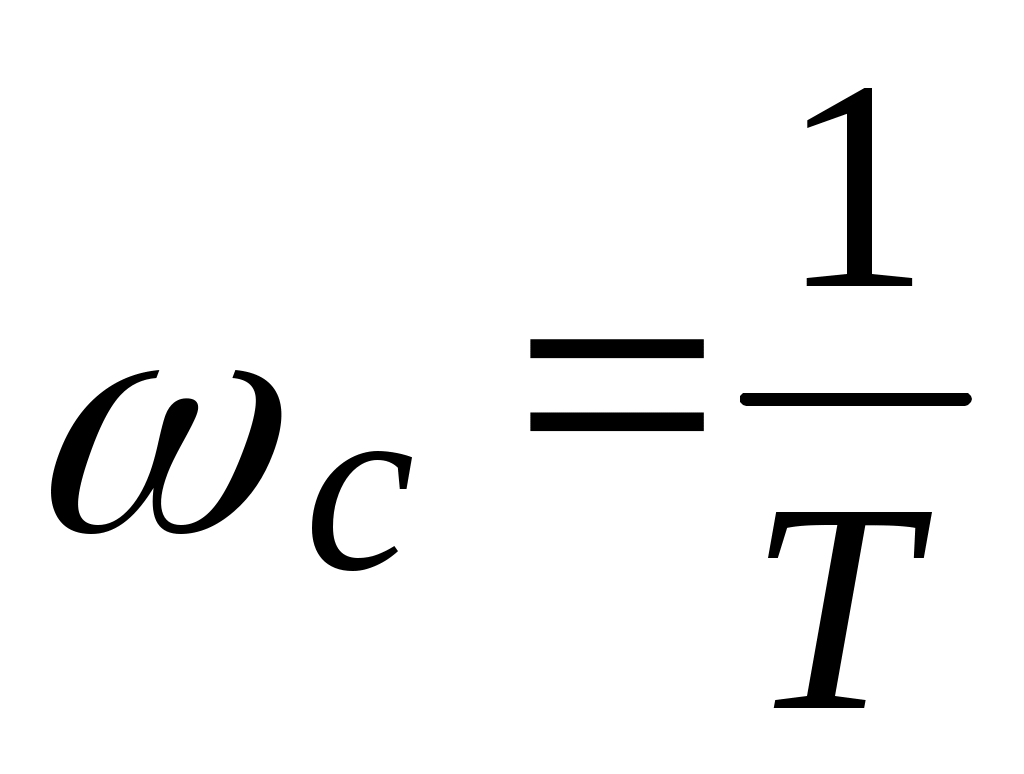 принимает значение принимает значение 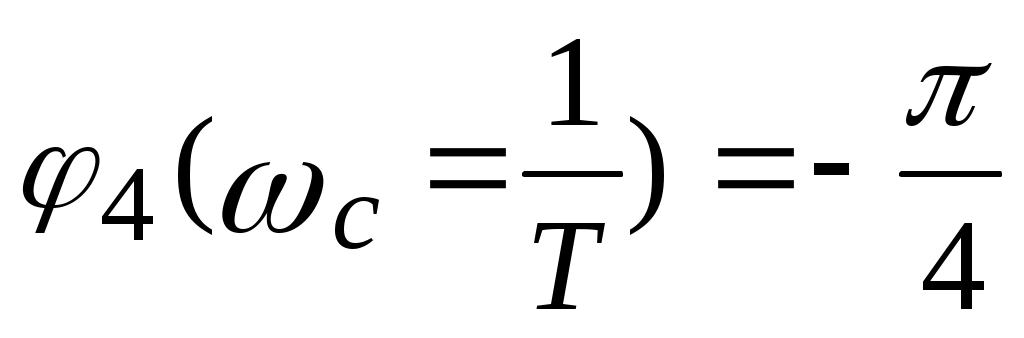
при уменьшении частоты относительно частоты сопряжения 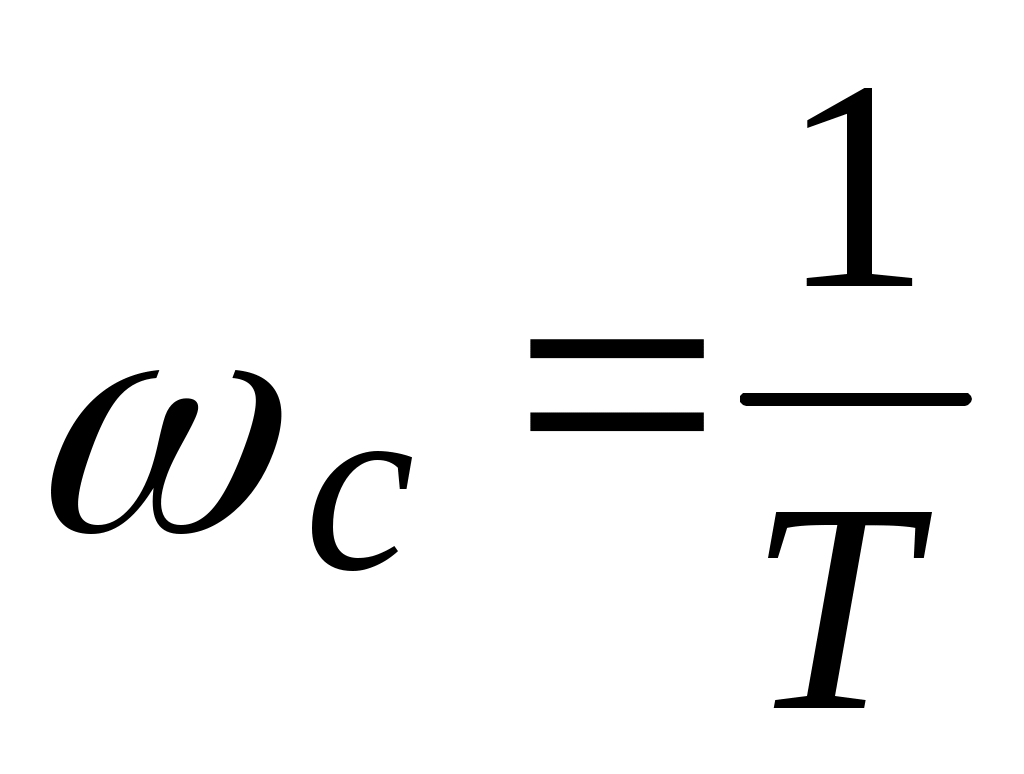 фазочастотная характеристика стремиться к нулю; фазочастотная характеристика стремиться к нулю;
при увеличении частоты относительно частоты сопряжения 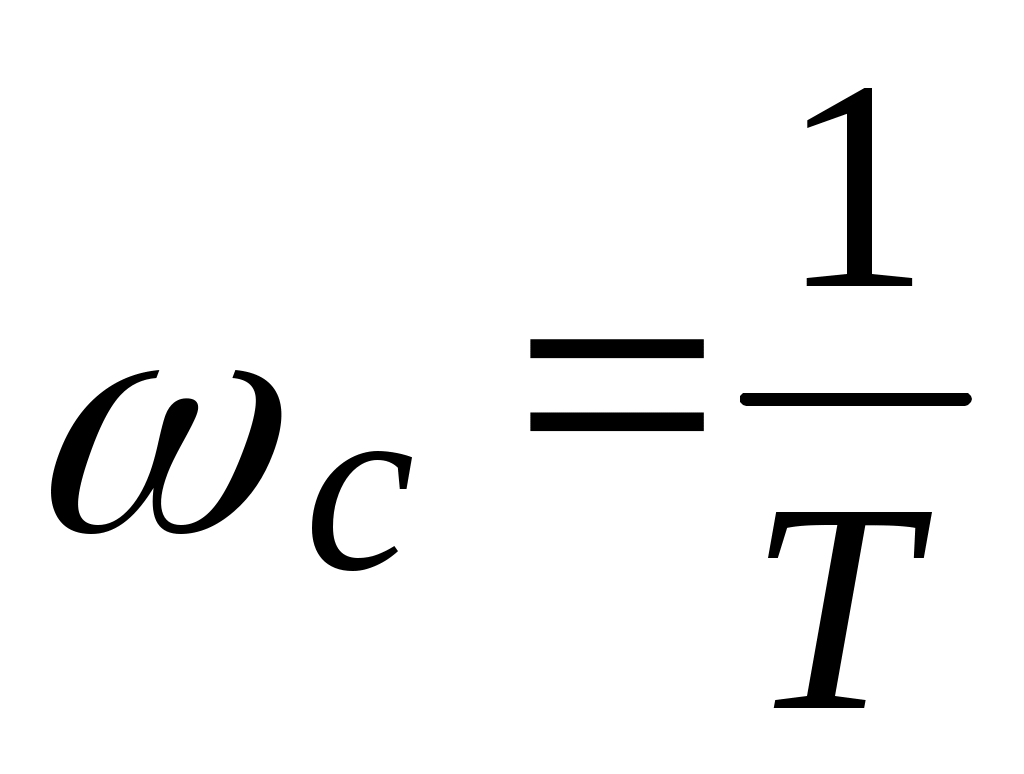 фазочастотная характеристика стремиться к значению фазочастотная характеристика стремиться к значению 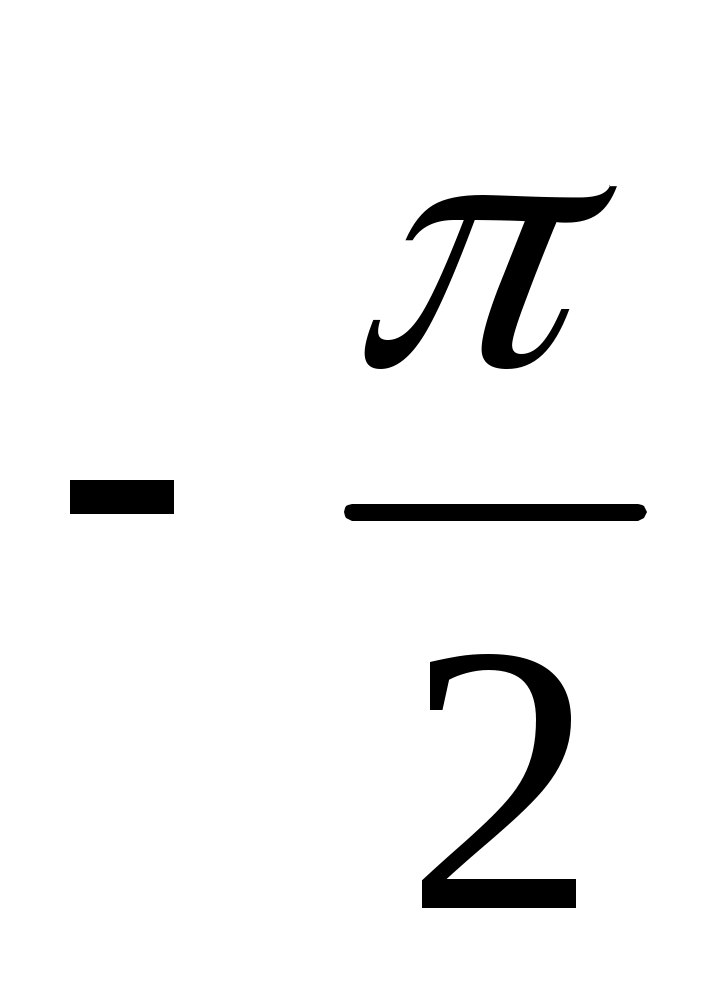 . .
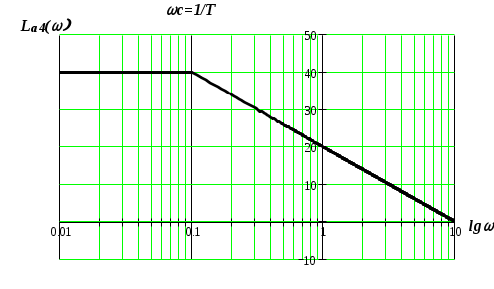
рис. 5.7. Асимптотическая логарифмическая амплитудная частотная характеристика инерционного звена
Для оценки неизвестных значений параметров K и T по ЛАЧХ необходимо построить низкочастотную асимптоту, имеющую нулевой наклон, и высокочастотную асимптоту, имеющую отрицательный наклон -20 дБ/дек. Точка пересечения этих асимптот дает частоту сопряжения 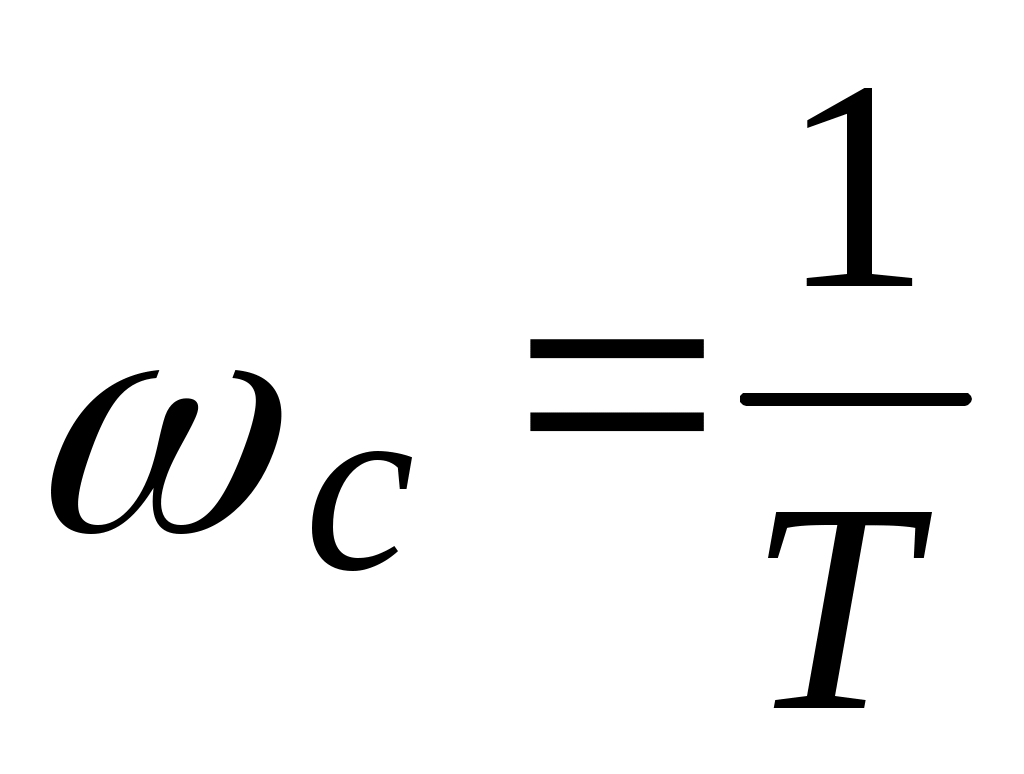 и ординату, соответствующую значению и ординату, соответствующую значению 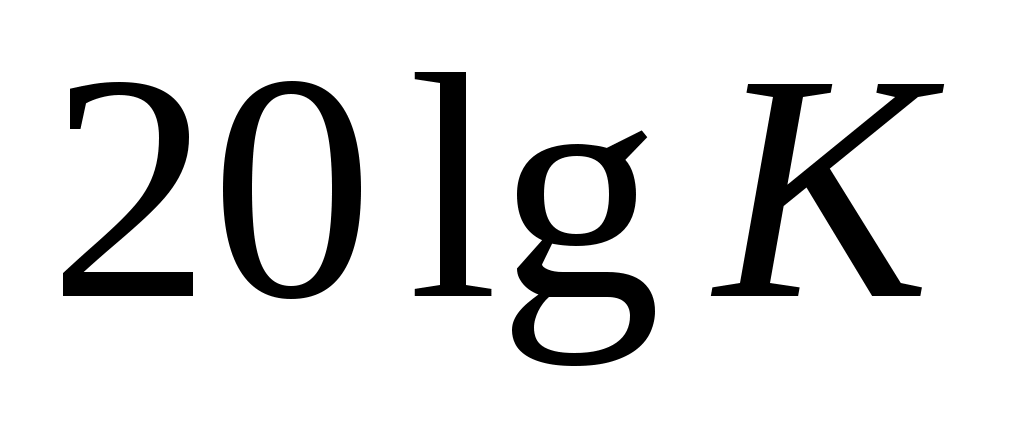 , т.е. на частоте , т.е. на частоте 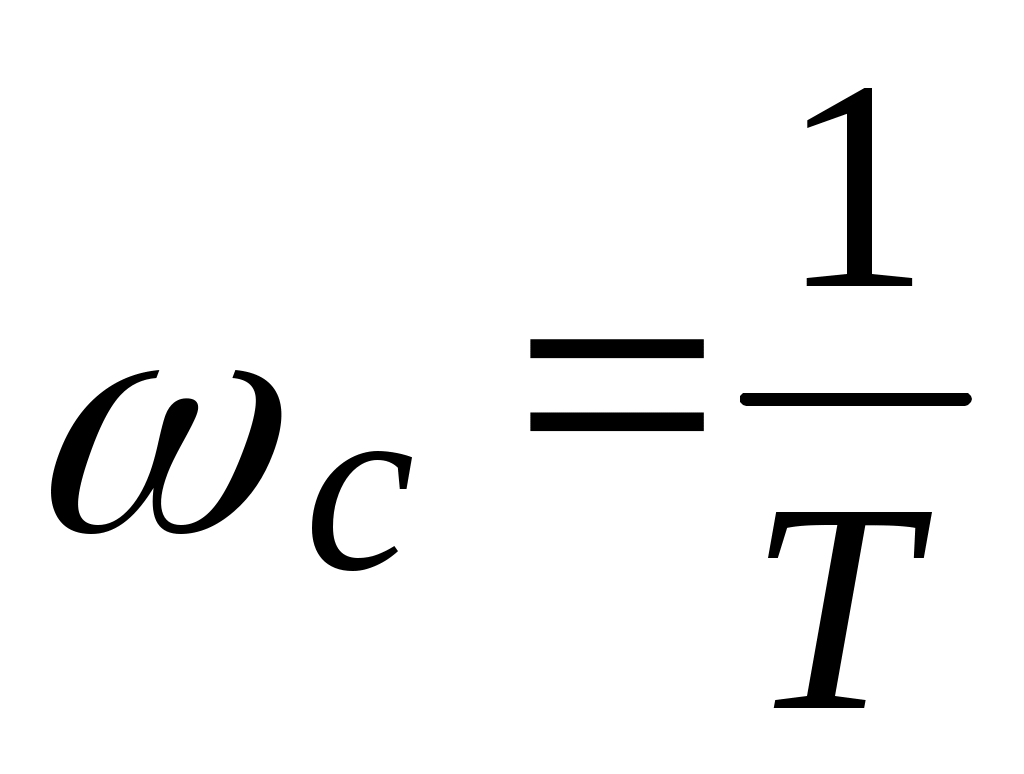 значение значение 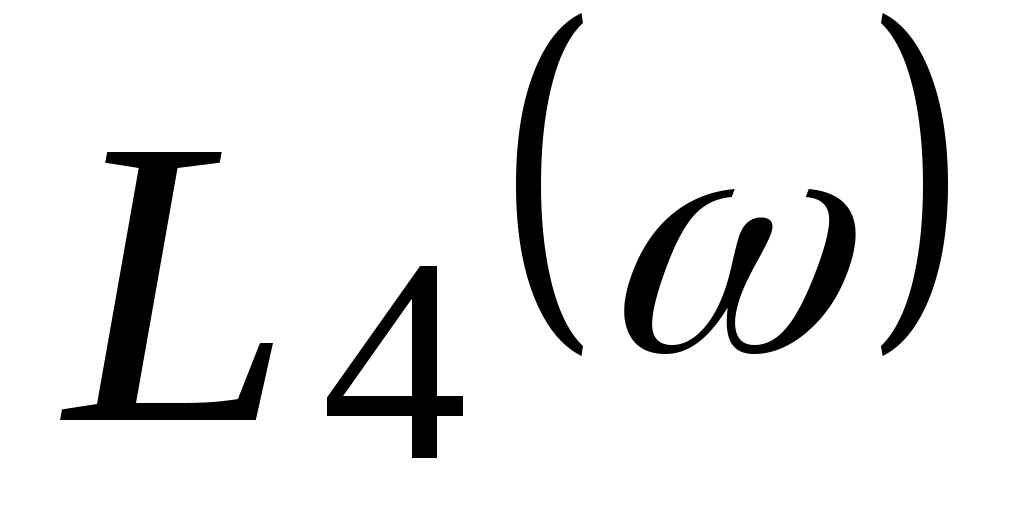 равно равно 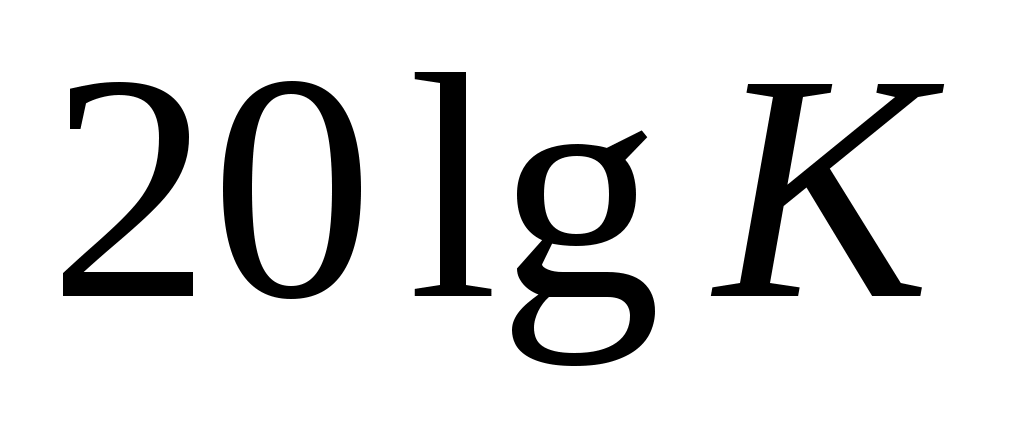 . .
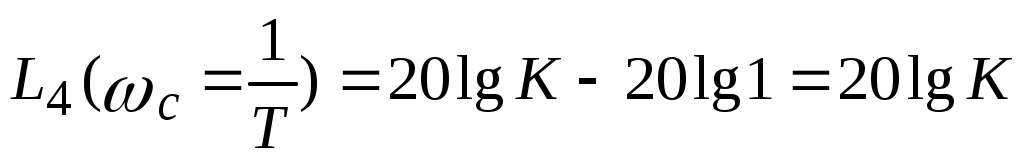
Параметр K находится по формуле 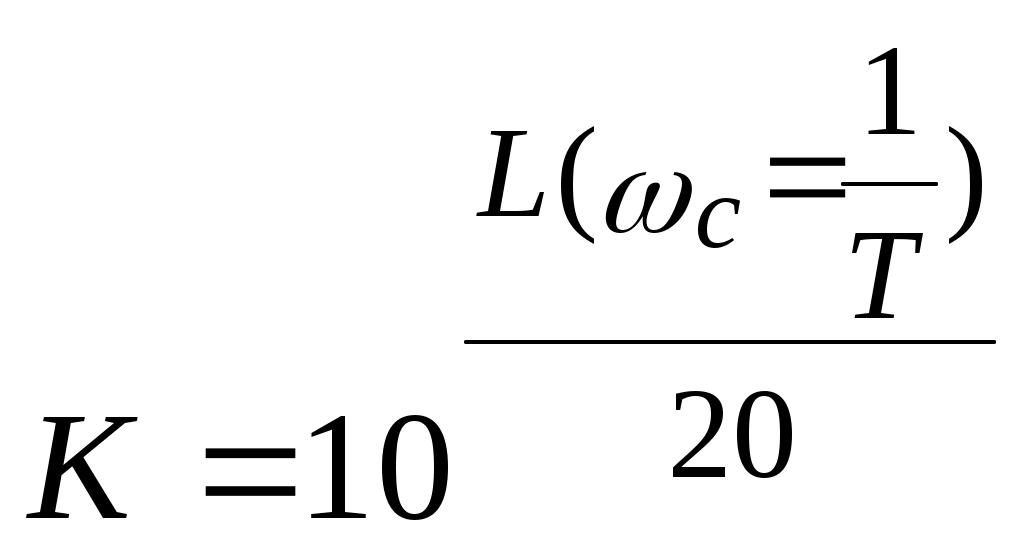 . .
для определения значения T нужно воспользоваться выражением 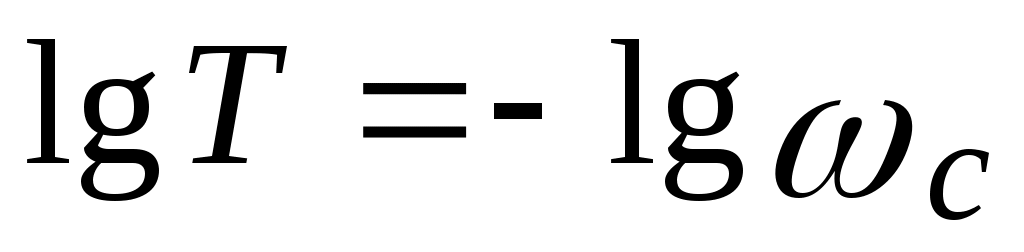 или или 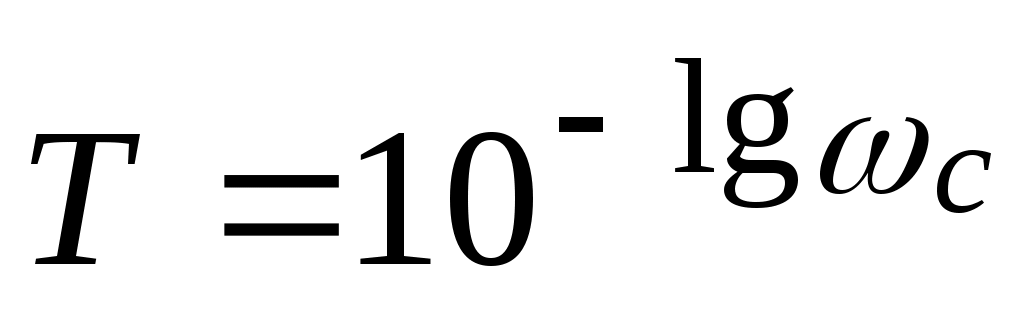 , , 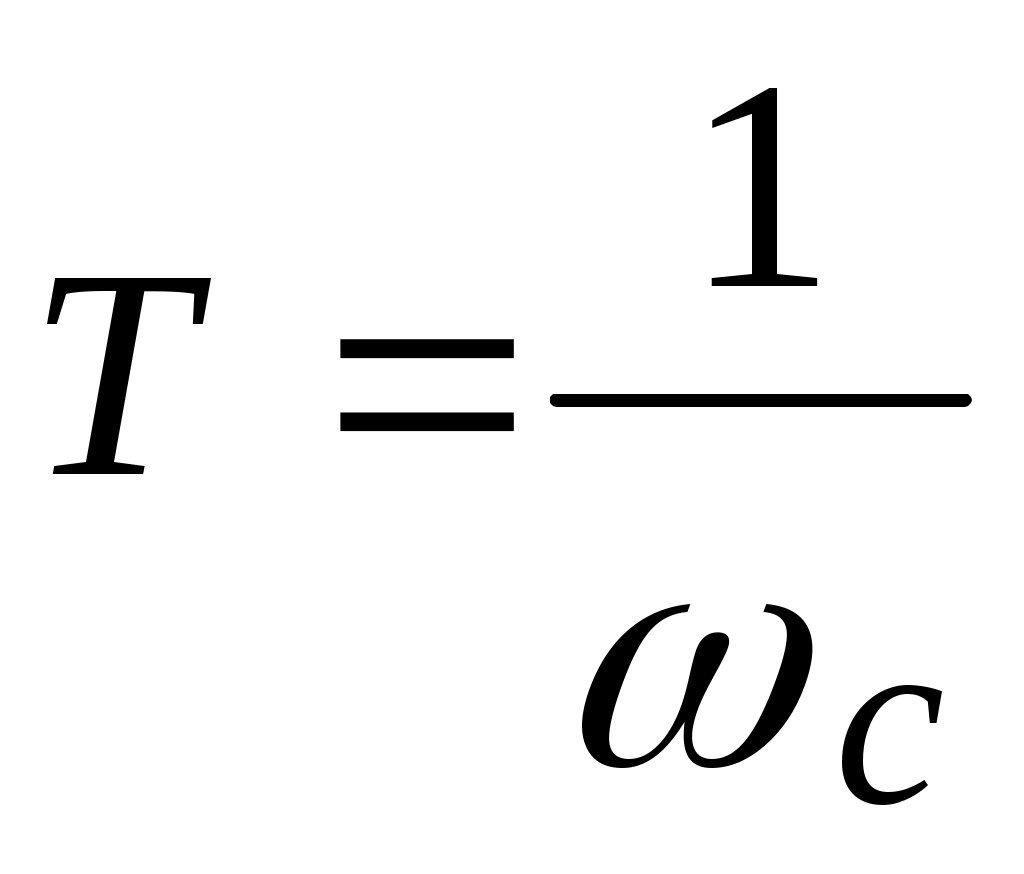 . .
Пример расчета асимптотических логарифмических частотных характеристик. Задана передаточная функция инерционного типового звена первого порядка: W(s)=k/(Ts+1), требуется рассчитать и построить асимптотическую ЛАЧХ.
Решение.
1. Заменим s на jω с учетом того, что 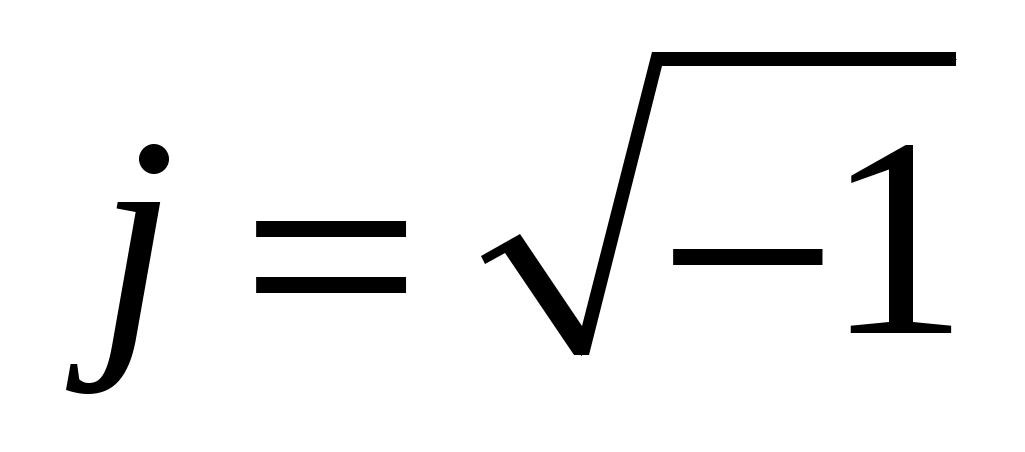 и путем несложных преобразований получим : W(jω)=k/(Tjω +1) и путем несложных преобразований получим : W(jω)=k/(Tjω +1)
2. Запишем выражение амплитуды W(ω):
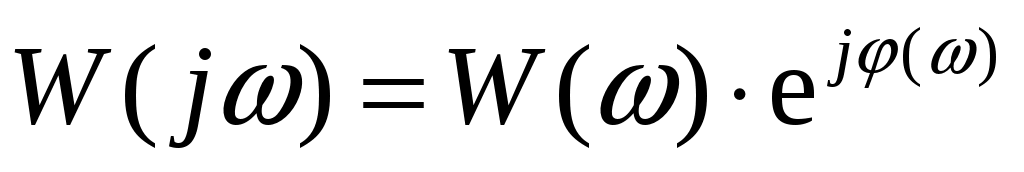
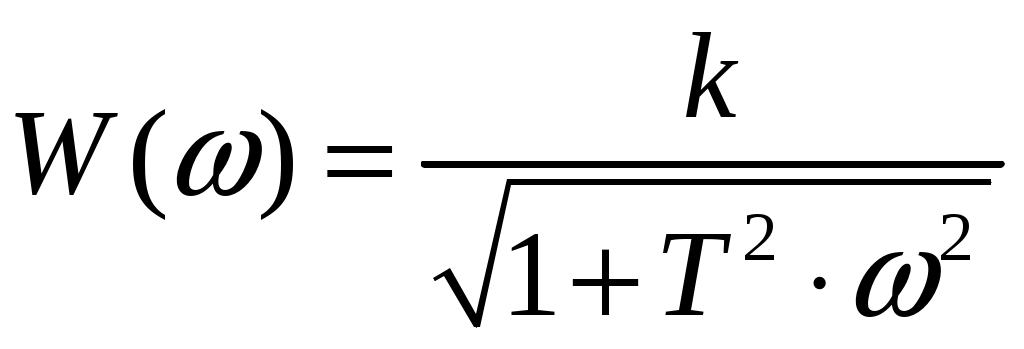
3. Запишем выражение ЛАЧХ L(ω):
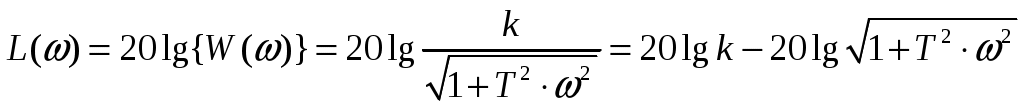
Следовательно, в низкочастотной области
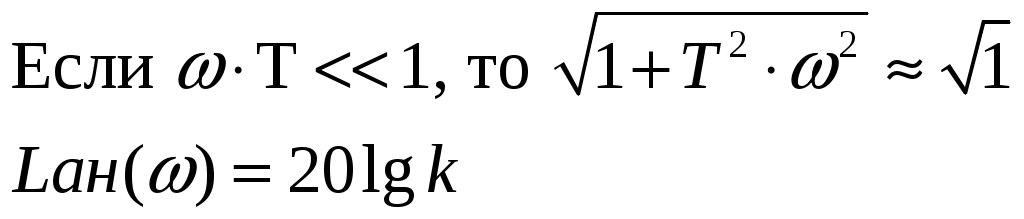
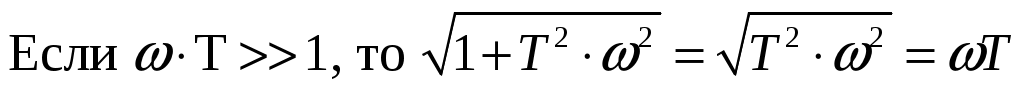
Следовательно, в области высокой частоты
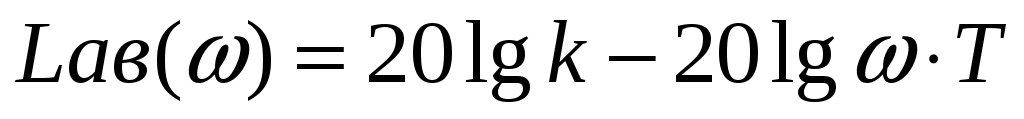
4. Частоты, соответствующие точкам сопряжения отрезков, называются сопрягающими и обозначаются ωс=1/Т
5. Строим график ЛАЧХ:
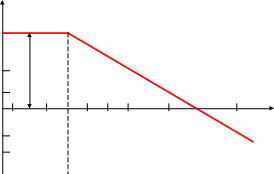 L( L( ), дБ ), дБ
20
20lgk -20дБ\дек
10
lg
0,1 0,5 ωс=1/Т 1 2 5 10 100 
-10
-20 Низкочастот- Высокочастотная область
ная область
Порядок выполнения работы
В соответствии с вариантом задания в табл.4.1. произвести построение частотных характеристик типовых звеньев первого порядка и графоаналитическим способом рассчитать их параметры.
Вычисление частотных характеристик звена или системы
Пусть задана передаточная функция звена, например:
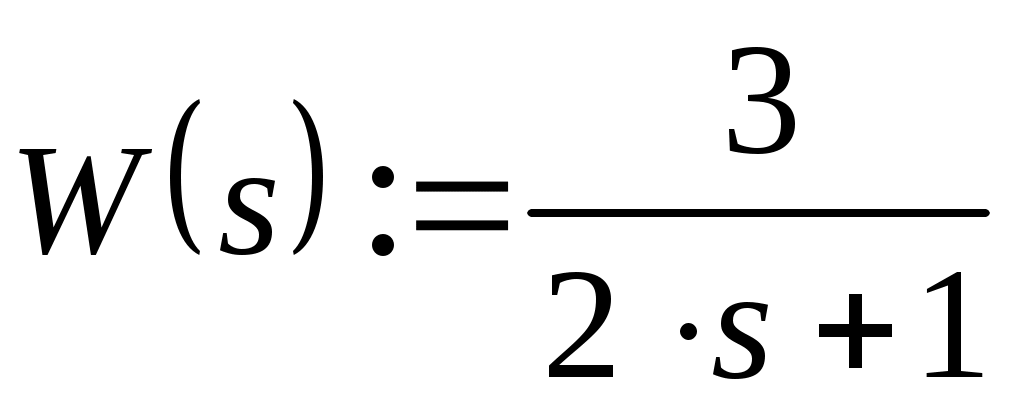
Найдём комплексный коэффициент передачи, заменив переменную s на j Для этого введём мнимую единицу 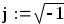 . .
Для этого заменим s (оператор Лапласа) на (jω) :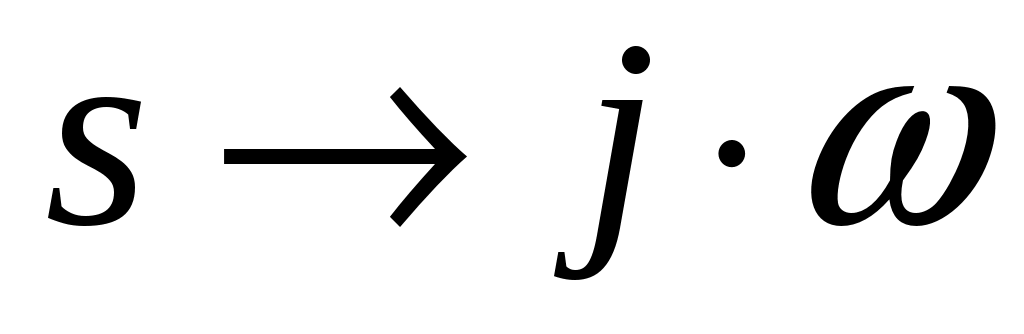 с учетом того, что с учетом того, что 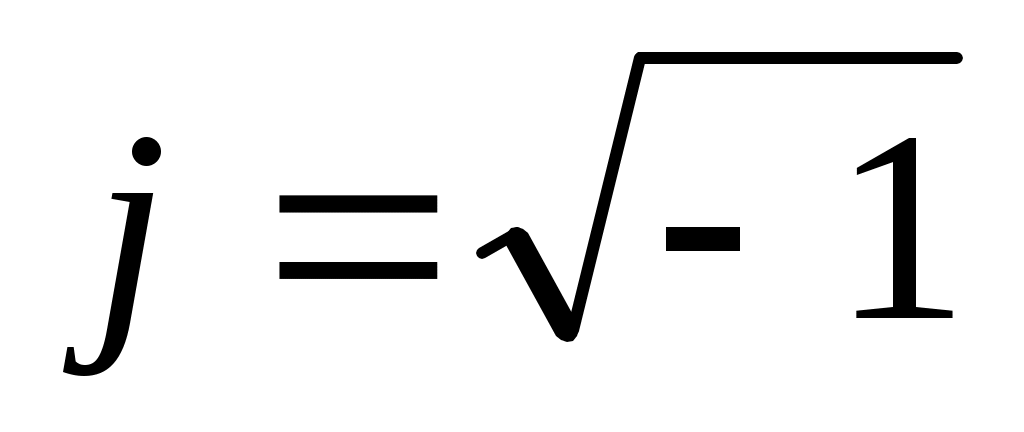 и путем несложных преобразований - подстановку комплексной переменной и перемножение числителя и знаменателя на комплексно сопряженное число получим: и путем несложных преобразований - подстановку комплексной переменной и перемножение числителя и знаменателя на комплексно сопряженное число получим:
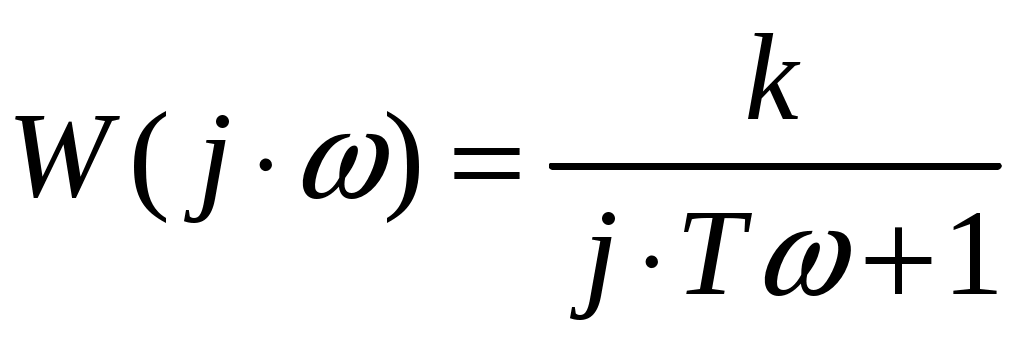 , ,
Избавляясь от мнимой единицы j в знаменателе (иррациональности), получаем комплексный коэффициент передачи в виде:
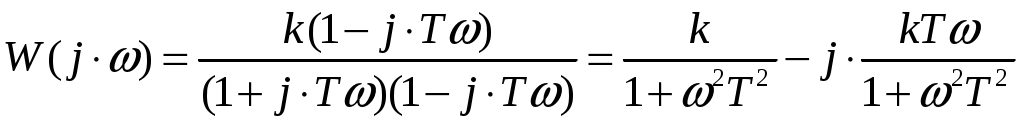 . .
Вещественная часть ККП:
|
Мнимая часть ККП:
|
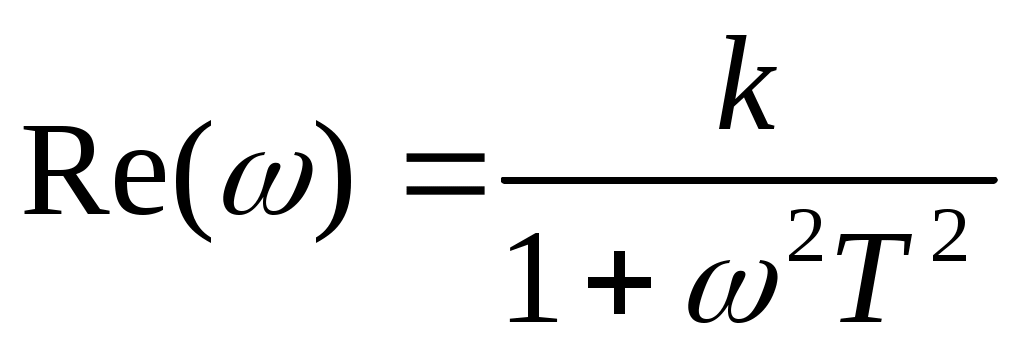 . .
|
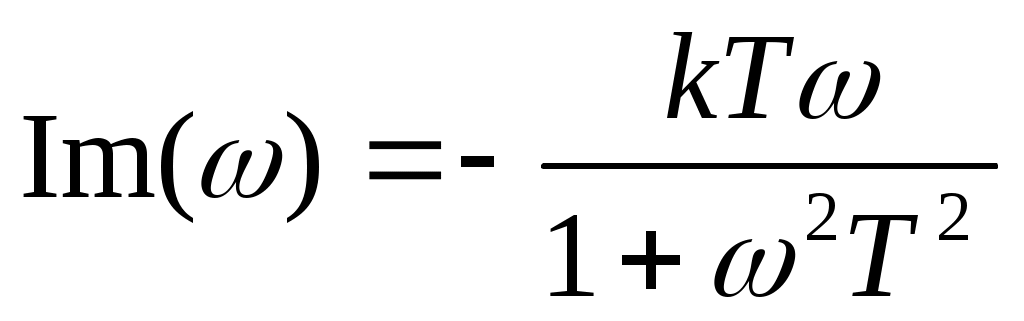 . .
|
Запишем комплексный коэффициент передачи формальной заменой s на jω в передаточной функции разомкнутой системы и выведем полученное выражение на экран с помощью «символьной стрелки», вызываемой также из палитры Символьные операторы:
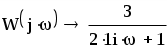
Для нахождения вещественной 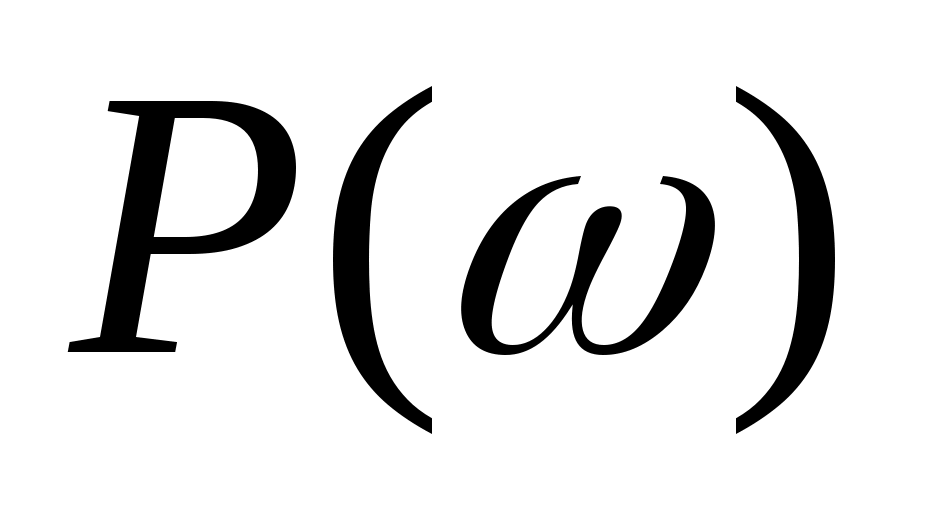 и мнимой и мнимой 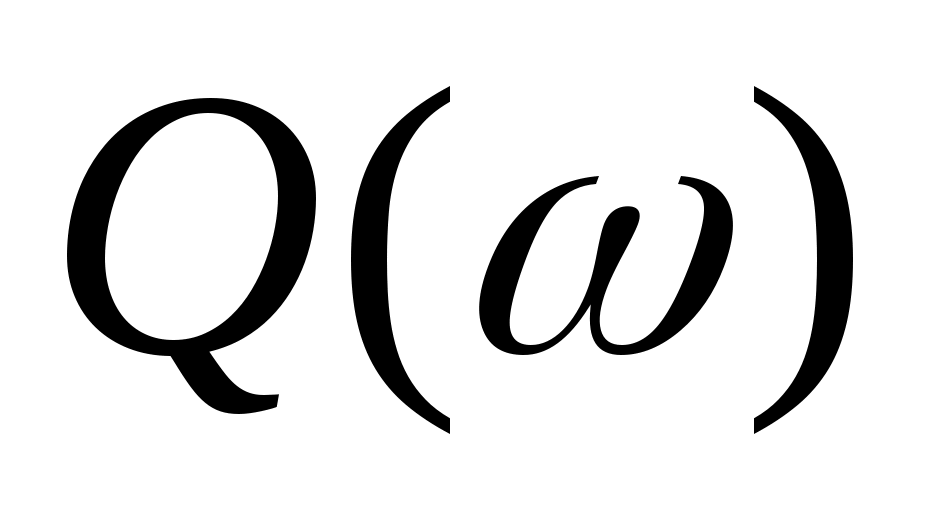 частотных характеристик звена воспользуемся стандартными функциями Mathcad: Re() и Im() соответственно: частотных характеристик звена воспользуемся стандартными функциями Mathcad: Re() и Im() соответственно:
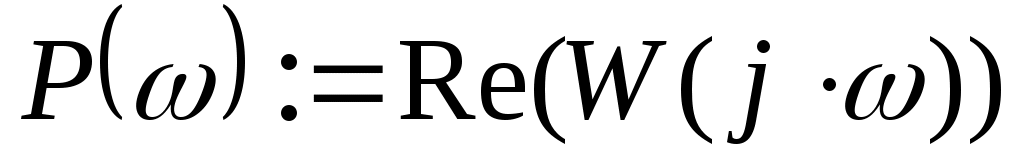 , ,
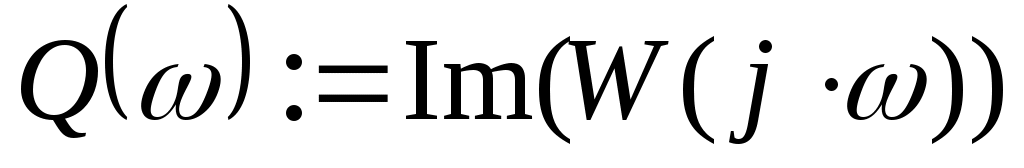
Для нахождения вещественной и мнимой частей выражения в Mathcad имеются специализированные встроенные функции:

Выбрать из командной строки опцию «вставка функции» f(x) и из предложенного списка слева – категория функции – комплексные числа (Complex Number), из предложенного списка справа – имя функции Re() или Im() – далее клик по кнопке «ОК» или «добавить».
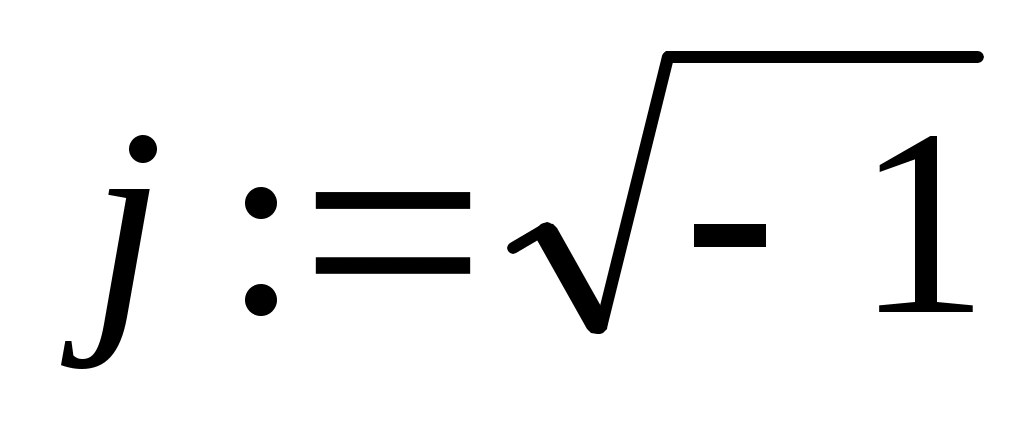
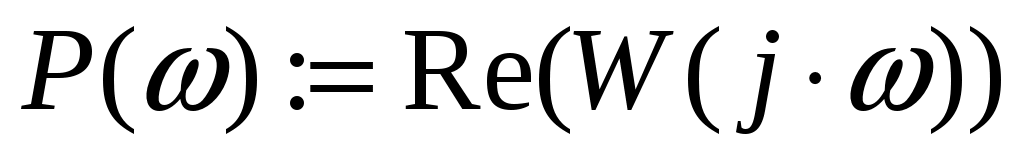
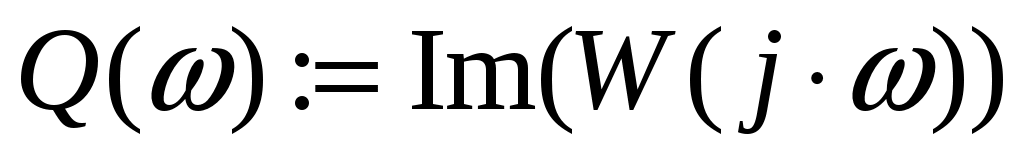
Однако возможности Mathcad не позволяют сразу получить комплексный коэффициент передачи в виде суммы вещественной и мнимой частей.
При этом следует учесть, что комплексный коэффициент передачи может быть представлен в виде
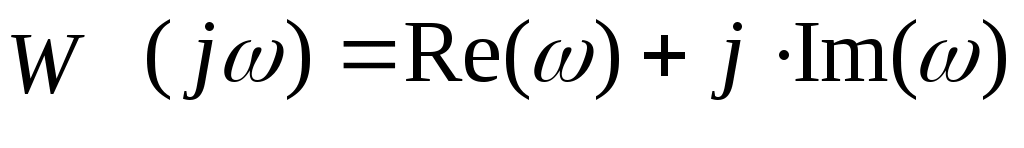 , ,
где 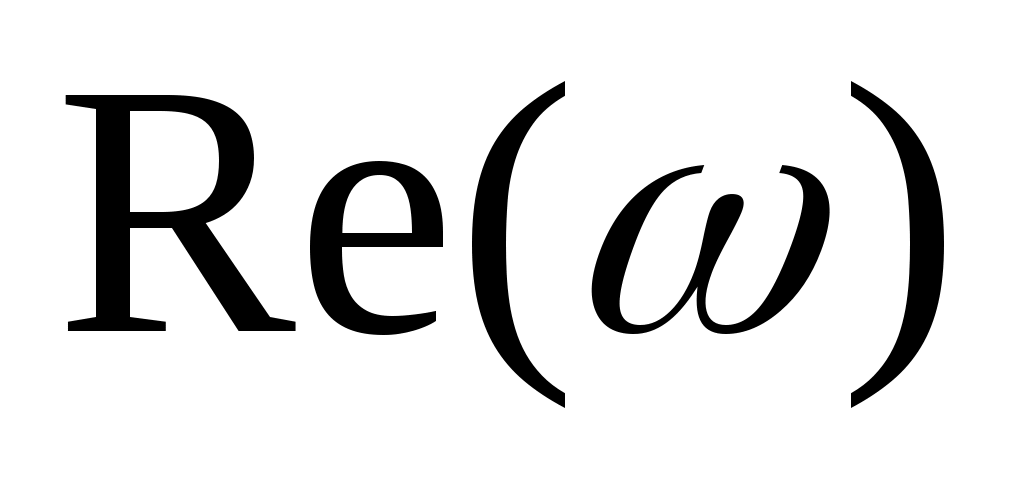 - вещественная часть комплексного коэффициента передачи, - вещественная часть комплексного коэффициента передачи,
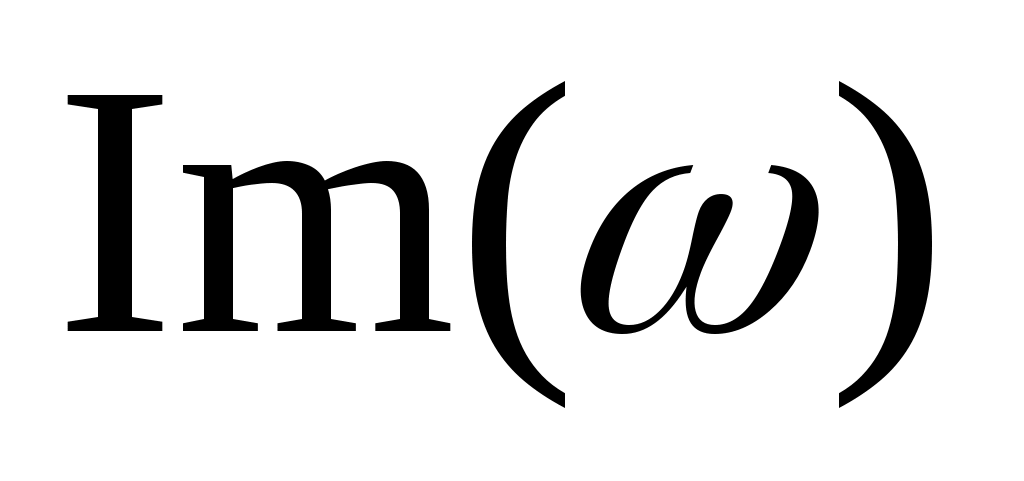 - мнимая часть комплексного коэффициента передачи. - мнимая часть комплексного коэффициента передачи.
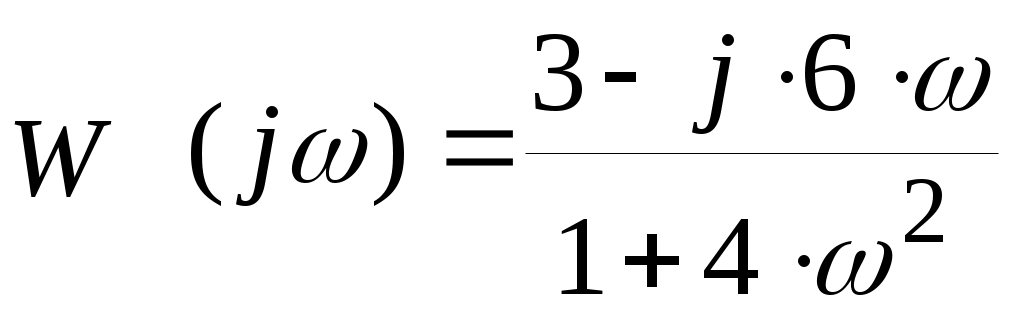
Тогда мнимая и вещественная части будут равны:
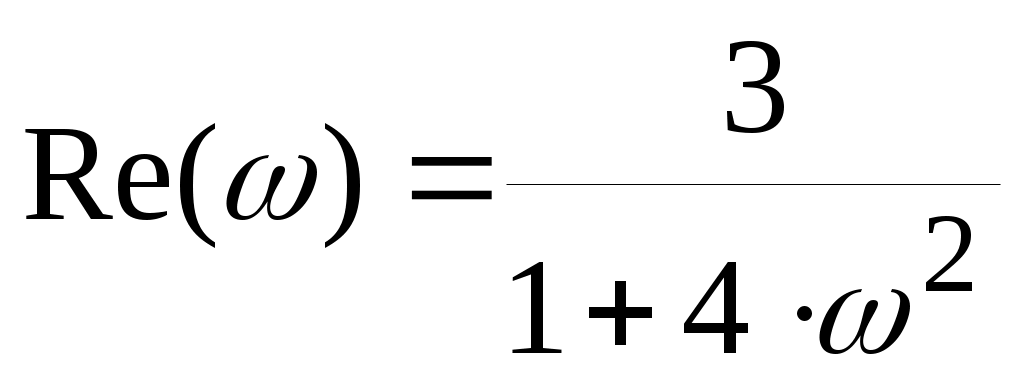
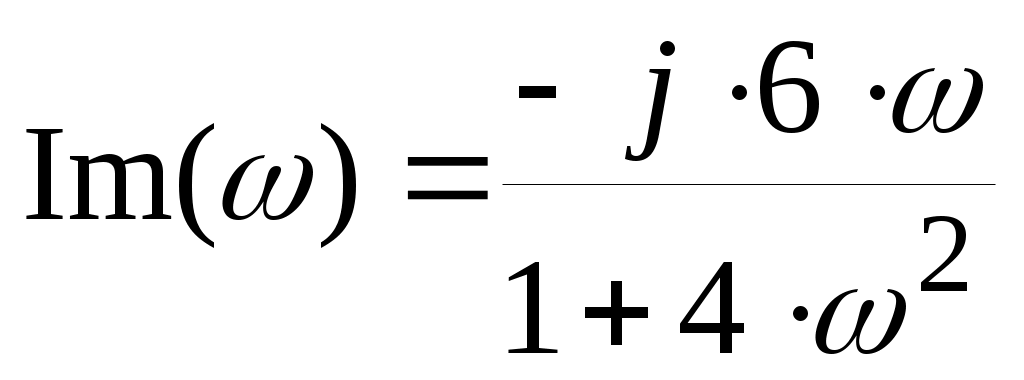
Для построения годографа АФЧХ звена зададим диапазон и шаг изменения аргумента (частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»:
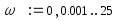
Далее из палитры Инструменты графиков вызовем поле декартовых координат (Ctrl+2), где в позиции на оси абсцисс запишем P(ω), а на оси ординат – Q(ω):
Для построения вещественной 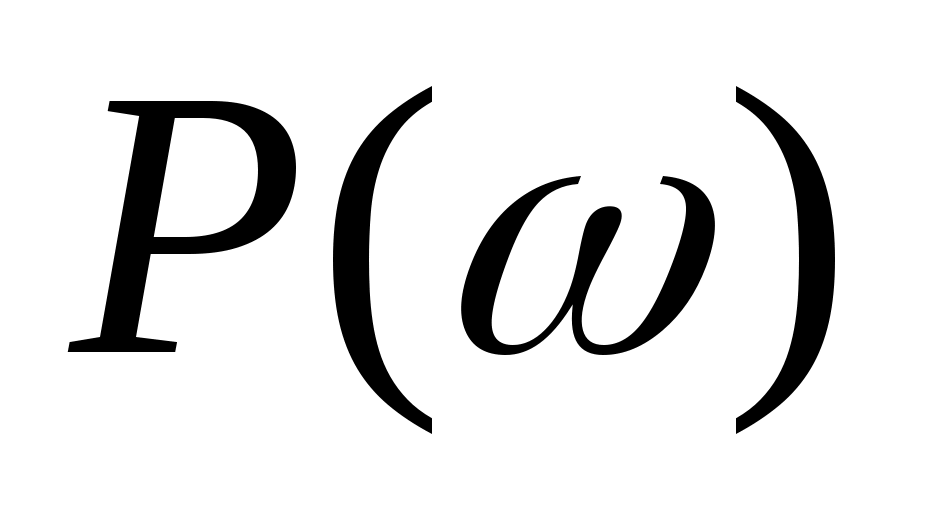 и мнимой и мнимой 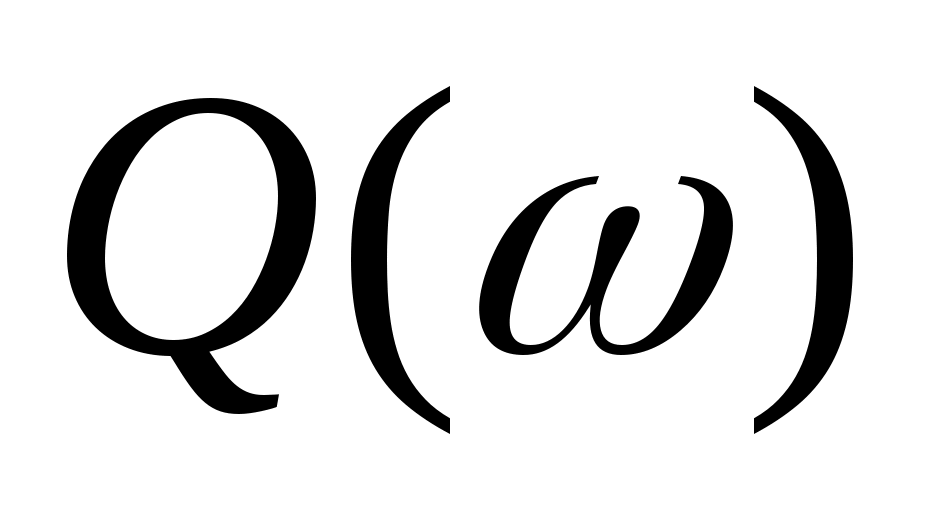 частотных характеристик звена зададим диапазон и шаг изменения аргумента (частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»: частотных характеристик звена зададим диапазон и шаг изменения аргумента (частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»:
: =0, 0.1 .. 1000
Далее из палитры Инструменты графиков вызовем поле декартовых координат (Ctrl+2), где в позиции на оси абсцисс запишем , а на оси ординат –P(ω) или Q(ω):
Теперь определим амплитудную-частотную (АЧХ) и фазовую частотную (ФЧХ) характеристики. По определению, АЧХ вычисляется как модуль комплексного коэффициента передачи, а ФЧХ - как его аргумент:
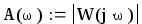 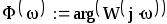
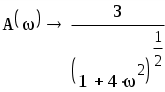
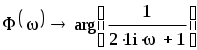
Действительная логарифмическая АЧХ в соответствии с определением вычисляется по формуле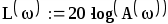 : :
Д
ля построения логарифмических частотных характеристик из палитры Инструменты графиков вызовем поле координат (Ctrl+2), где в позиции на оси ординат запишем логарифмическую АЧХL() или фазовую частотную характеристику (), а на оси абсцисс задаем логарифмический масштаб - lg.
Далее произвести построение асимптотических логарифмических частотных характеристик системы автоматического регулирования по вариантам заданий 4-ой лабораторной работы в соответствии с методикой изложенной выше в п.4.2.4.

|
|
|
 Скачать 1.02 Mb.
Скачать 1.02 Mb. Логарифмическая частотная характеристика (ЛАЧХ) – частотная характеристика в логарифмическом масштабе.
Логарифмическая частотная характеристика (ЛАЧХ) – частотная характеристика в логарифмическом масштабе.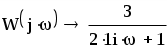

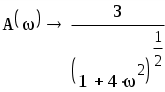



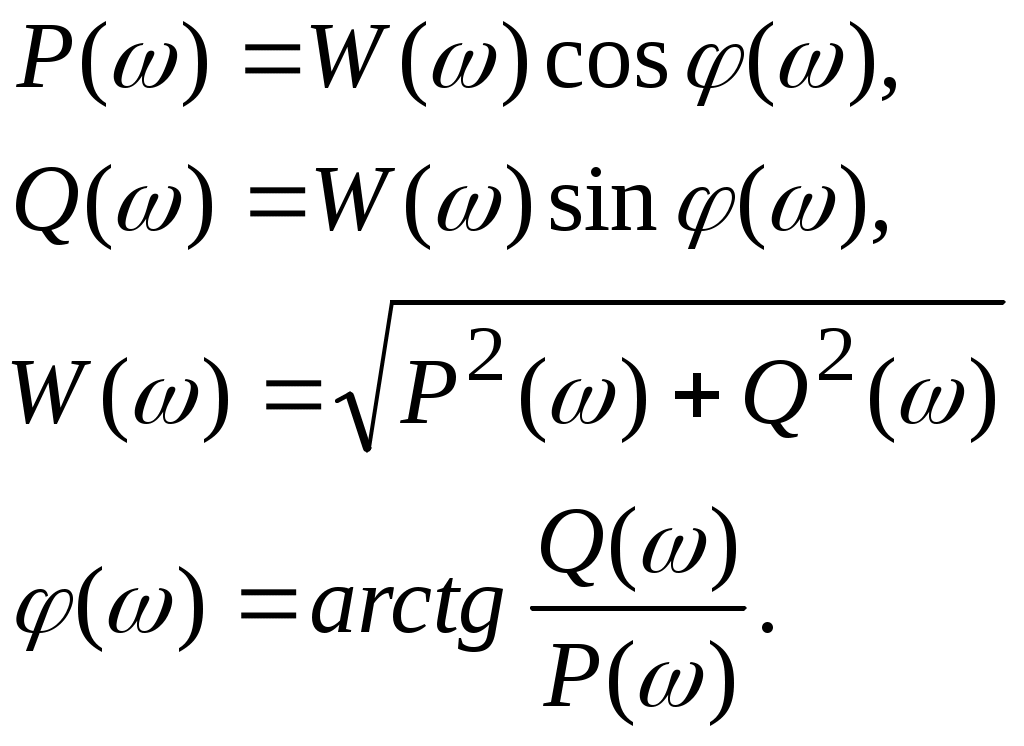
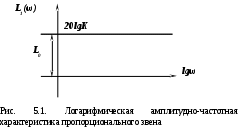




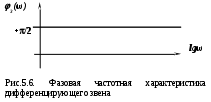
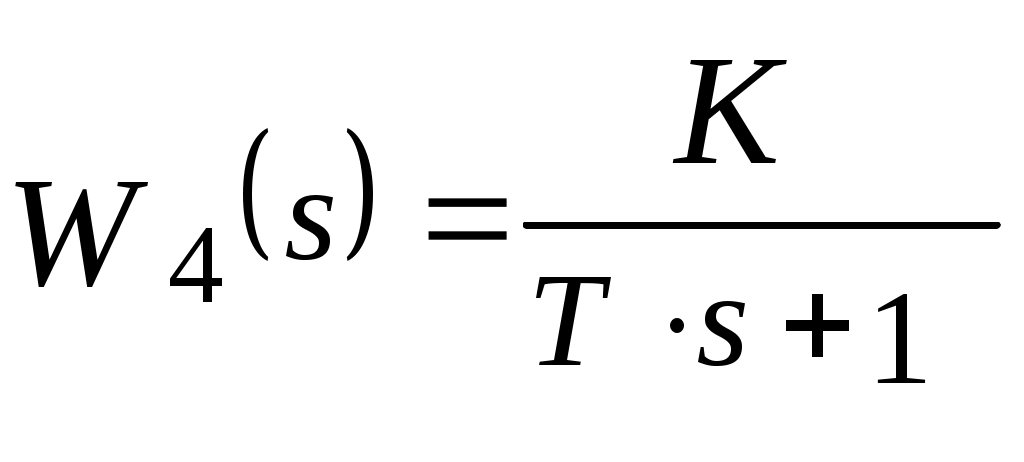 .
.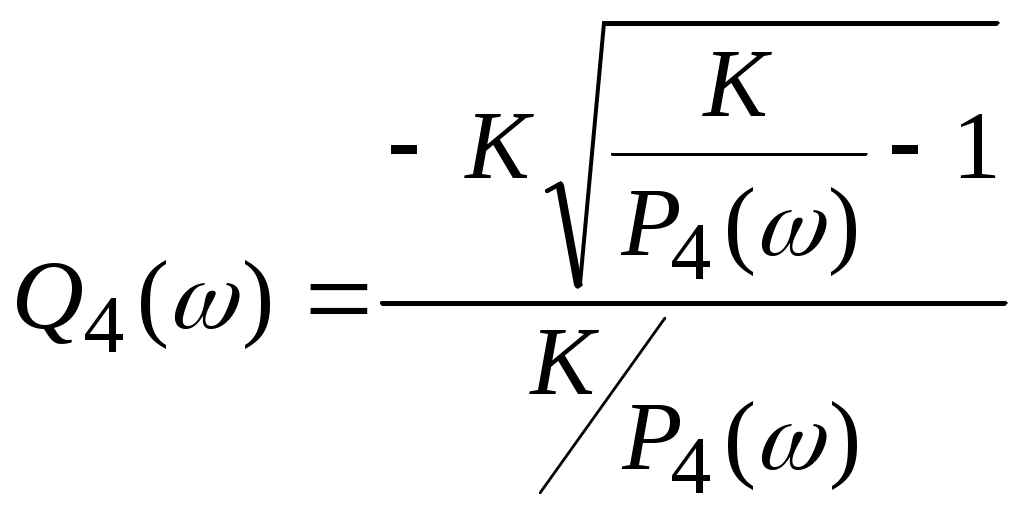 . Преобразуя эту зависимость, имеем:
. Преобразуя эту зависимость, имеем: 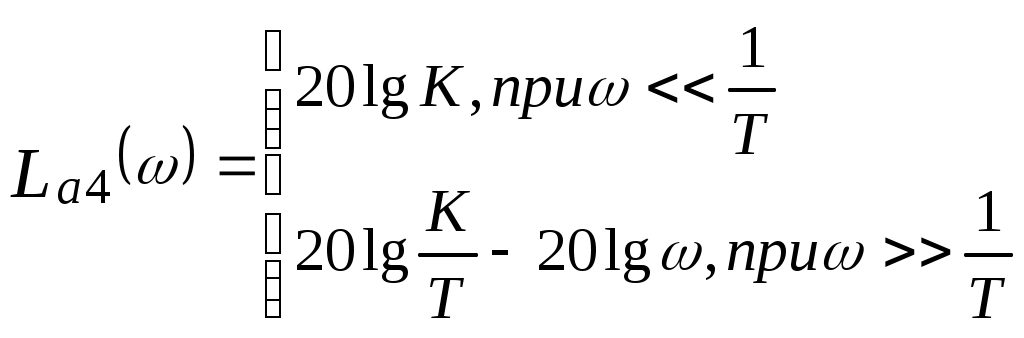

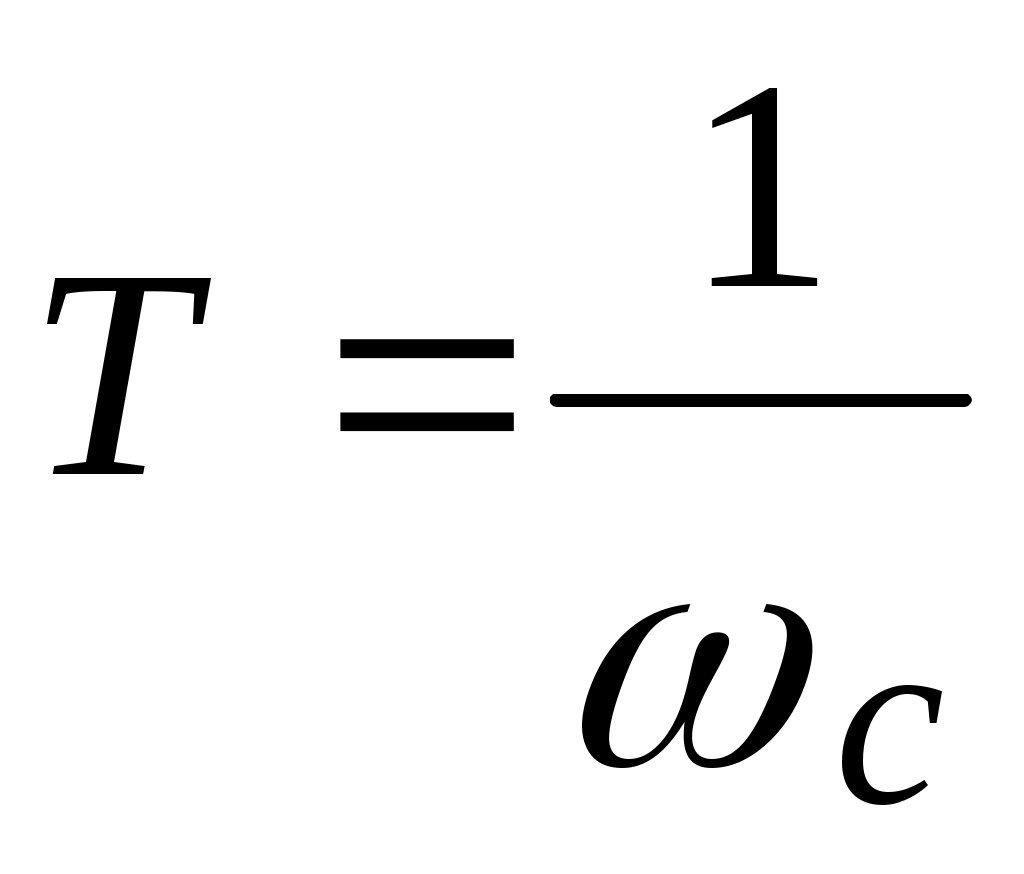 .
.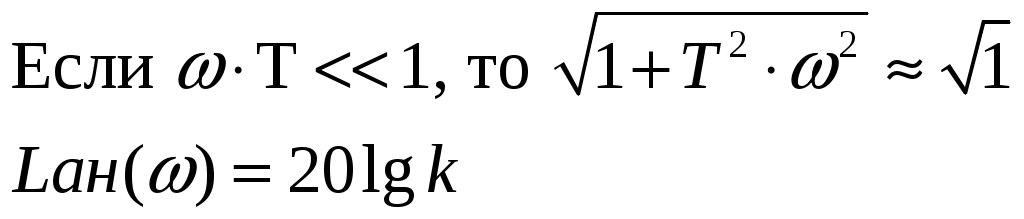
 L(
L(