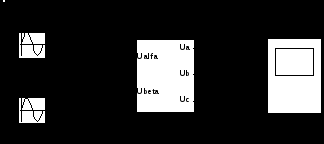диплом готово+. Рациональное использование водных и топливноэнергетических ресурсов, а также охрана окружающей среды определили направление развития систем водо и теплоснабжения
 Скачать 1.8 Mb.
|
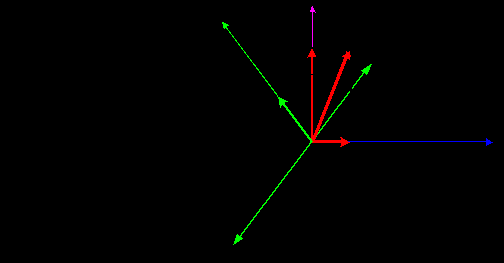
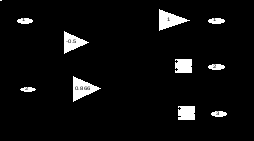
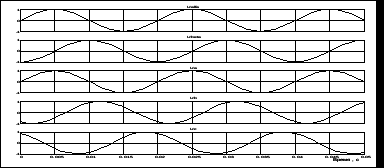
3.1.1 Преобразование трёхфазной в двухфазную систему. При построении реальных систем электропривода переменного тока, как асинхронных, так и синхронных, практически всегда в систему управления включают преобразователи фаз 3/2 и 2/3 [2].Первый (3/2) преобразовывает фазные напряжения трёхфазной системы в напряжения двухфазной системы в координатах α, β. Отметим, что как трёхосная координатная система А, В, С, так и двухосная α, β являются неподвижными системами. Пространственный вектор изображает результат совместного действия трёхфазной системы токов любой эквивалентной m – фазной и, в частности, двухфазной системы. Переход к двухфазной системе в математическом отношении эквивалентен рассмотрению пространственного вектора в новой прямоугольной системе координат α, β. Физический смысл такого преобразования координат состоит в замене реальной трёхфазной машины эквивалентной двухфазной моделью, характеризующейся тем же значением пространственного вектора. Такая замена переменных широко используется при математическом исследовании электрических машин с целью упрощения систем дифференциальных уравнений электрического равновесия статорных и роторных цепей. На рисунке 3.2 изображено преобразование координат. 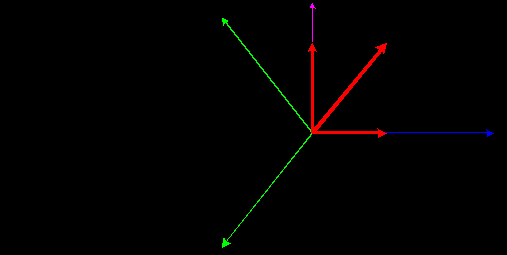 Рисунок 3.2 – Преобразование координат: а) условное графическое обозначение преобразователя; б) координаты Преобразователь (3.2) осуществляет преобразование трёхфазных напряжений UA, UB, UC (3.1) в двухфазные напряжения Uα, Uβ в соответствии с выражениями (3.2) и (3.3): 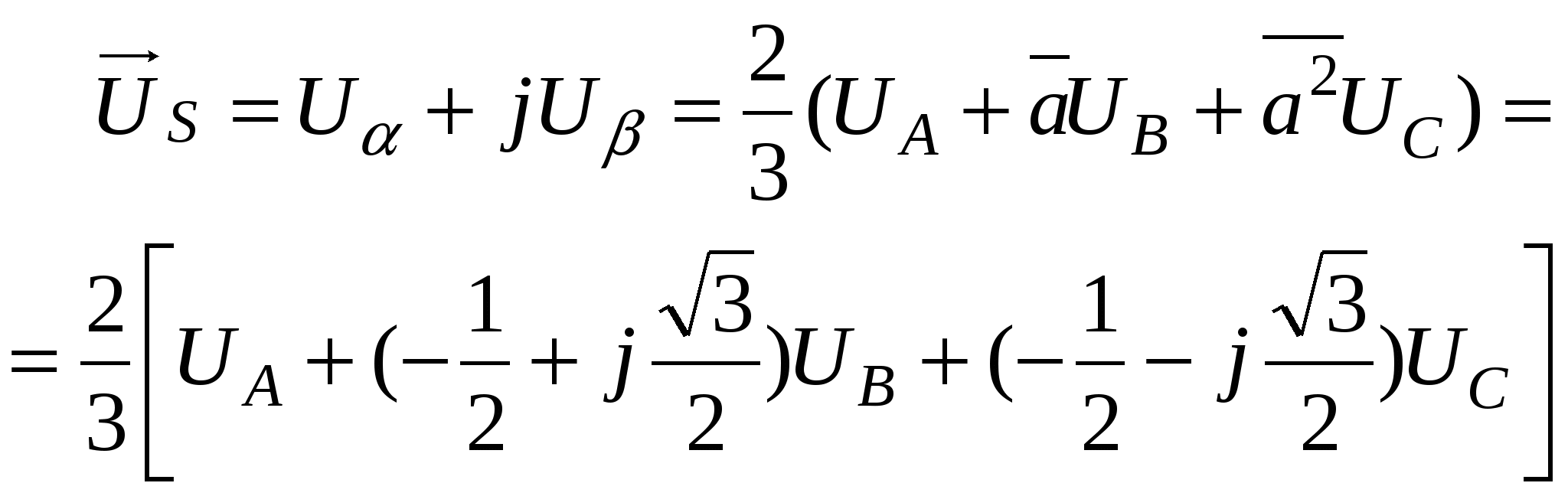 , (3.9)После преобразования (1.18) получим  , (3.10)При этом следует иметь в виду, что фазная ось α прямоугольной (двухфазной) системы совмещена с фазной осью А трёхфазной системы (рисунок 3.2,б). На рисунке 3.3 показана модель преобразователя (3/2) в Simulink (Matlab) [2]. 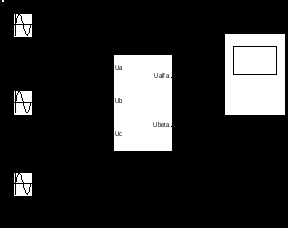 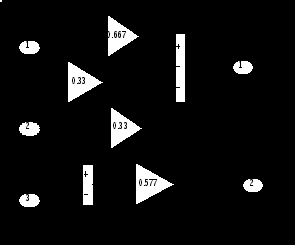 Рисунок 3.3 – Модель преобразователя На рисунке 3.4 показан результат преобразования трёхфазного напряжения в двухфазное. Амплитуда напряжения принята Um=1В, частота ω=314рад/сек (f=50Гц). Не трудно отметить, что пространственный вектор напряжения в координатах α, β описывается выражением (3.7), полученным для трёхфазной системы напряжений 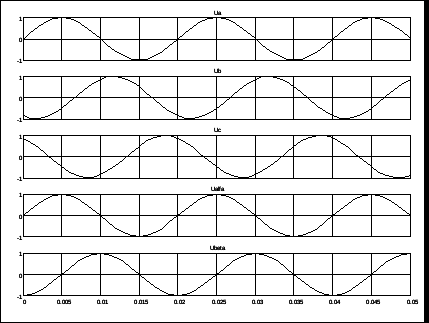 . Из (3.7) следует, что в двухфазной системе напряжения вычисляются, как  и  . Результаты расчета напряжений Uα и Uβ на модели позволяют сделать вывод, что пространственный вектор для трёхфазной и эквивалентной двухфазной систем одинаков и имеет выражение  . Рисунок 3.4 – Результаты преобразования 3-хфазной системы напряжений в двухфазное (Um=1В, f=50Гц) 3.1.2 Преобразователь двухфазной системы в трёхфазную. При разработке преобразователя (2/3) следует иметь в виду, что фазный вектор трехфазной системы |
представляет проекцию пространственного вектора 
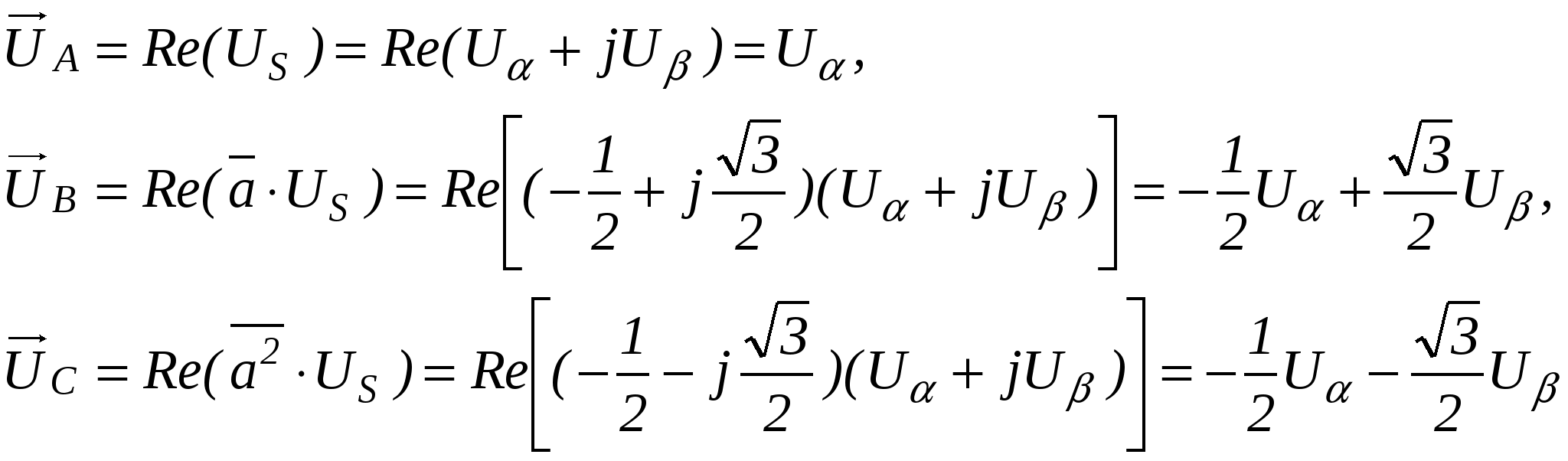(3.10)
для произвольного положения пространственного вектора 
