|
|
диплом готово+. Рациональное использование водных и топливноэнергетических ресурсов, а также охрана окружающей среды определили направление развития систем водо и теплоснабжения
3.1.3 Вращающаяся система координат. Вращающаяся система координат в общем случае может перемещаться относительно неподвижной с произвольной скоростью 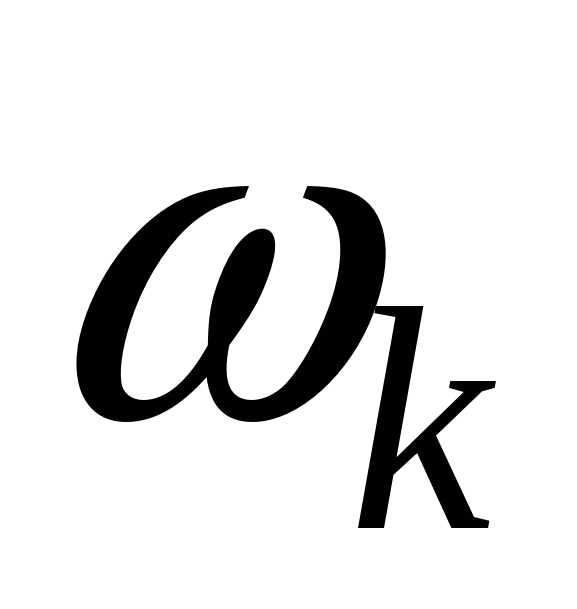 . Мгновенное положение такой системы координат относительно неподвижной определяется углом γ между вещественными осями систем координат. Положение пространственного вектора напряжения во вращающейся системе координат можно определить путем его поворота на угол γ против направления вращения. Поэтому между выражениями пространственного вектора . Мгновенное положение такой системы координат относительно неподвижной определяется углом γ между вещественными осями систем координат. Положение пространственного вектора напряжения во вращающейся системе координат можно определить путем его поворота на угол γ против направления вращения. Поэтому между выражениями пространственного вектора 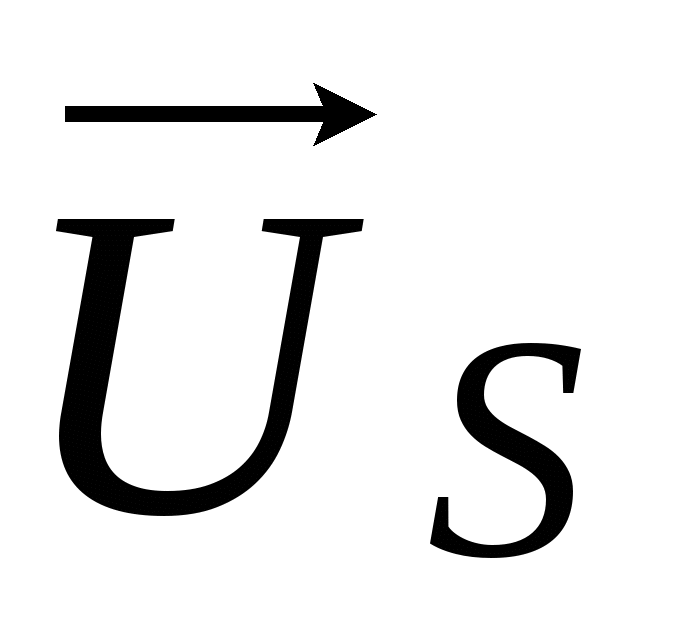 в неподвижной и в неподвижной и 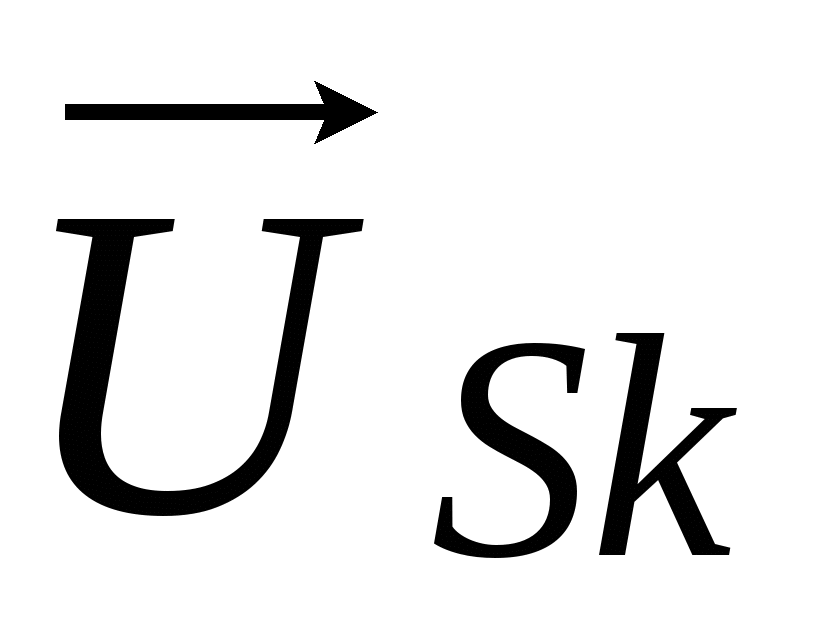 во вращающейся системах координат имеют место следующие соотношения [2]: во вращающейся системах координат имеют место следующие соотношения [2]:
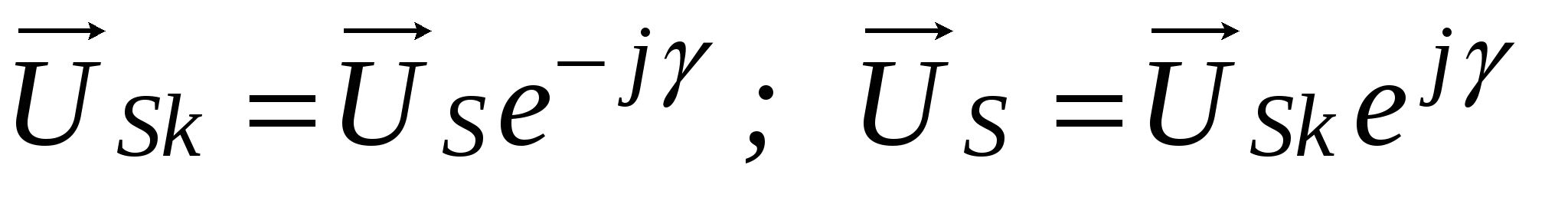 (3.11) (3.11)
Математическая основа преобразования координат поясняется на рисунке 3.8.
В неподвижной системе координат (α, β) пространственный вектор напряжения может быть представлен в алгебраической и показательной форме 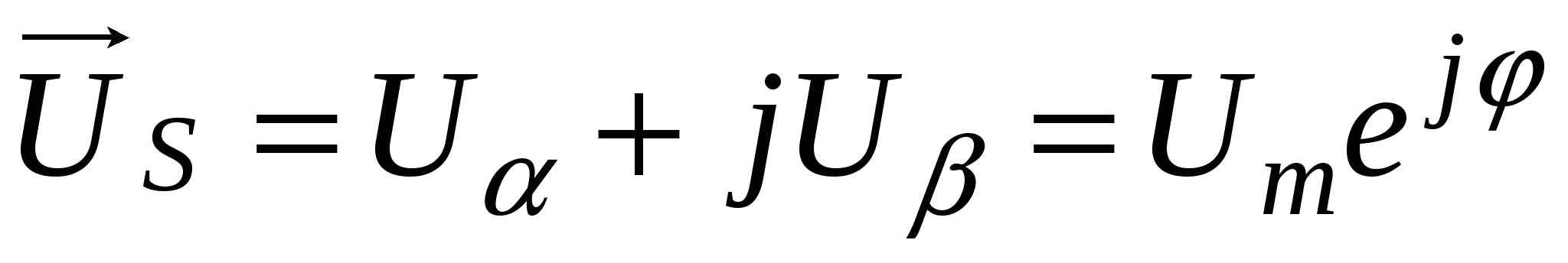 . .
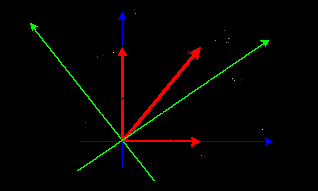
Рисунок 3.8 – Преобразование координат
Аналогично в системе вращающихся координат (х, у) тот же самый вектор может быть представлен в виде:
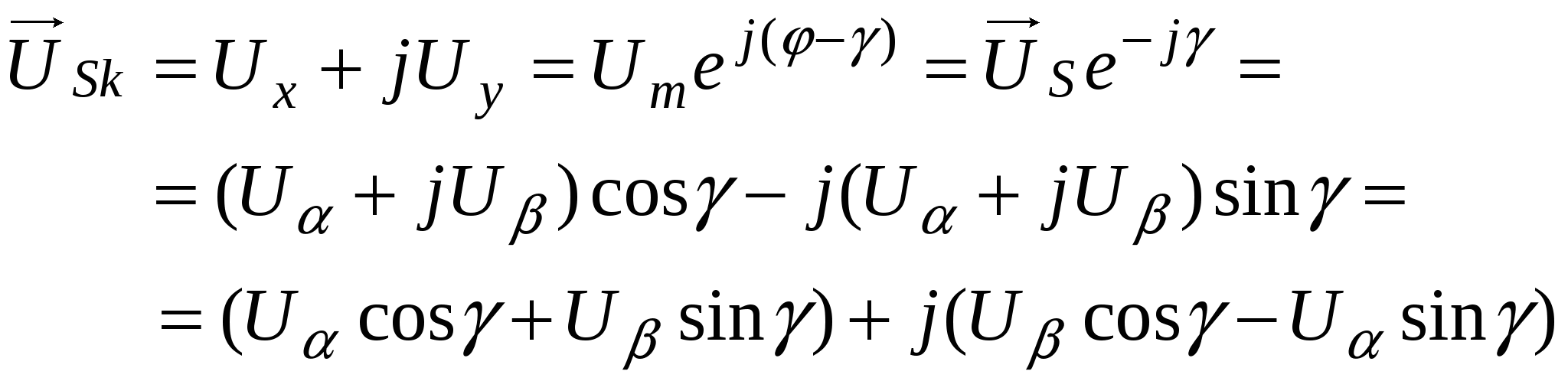 , (3.12) , (3.12)
Из выражения (3.12) получаем уравнения перехода от неподвижной системы координат к вращающейся:
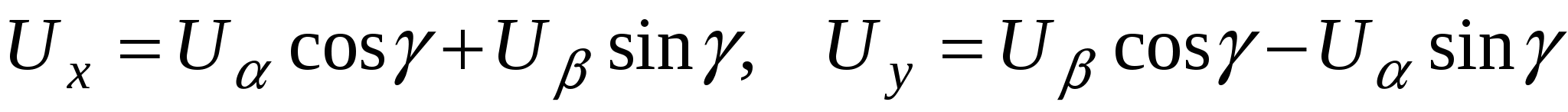 . (3.13) . (3.13)
Аналогично получаем уравнения перехода от вращающейся системы координат к неподвижной с учетом (3.11):
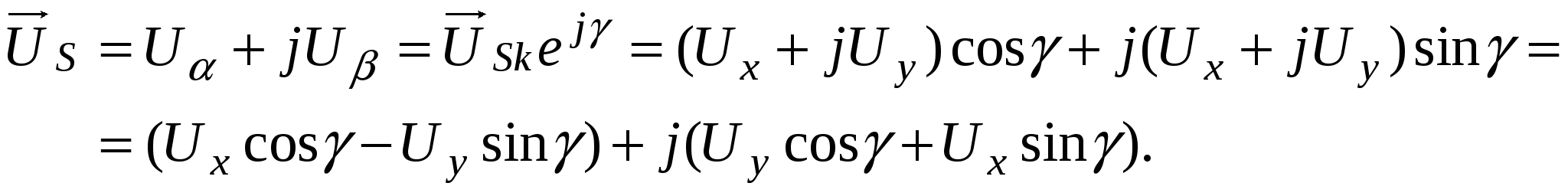
Тогда
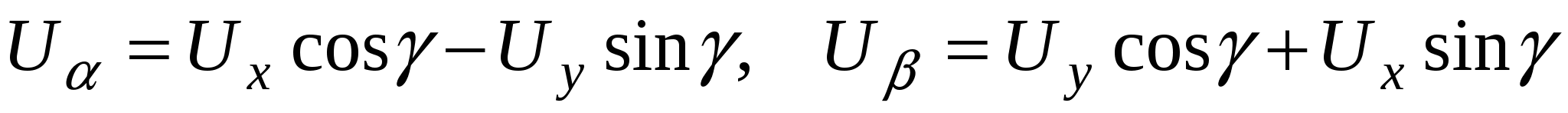 , (3.14) , (3.14)
На рисунке 3.9 представлена модель преобразователя неподвижной системы координат во вращающуюся, реализованную по уравнениям (3.13). На вход модели поданы проекции пространственного вектора напряжения на оси (α, β) в виде синусоидальных напряжений частоты 314 рад/сек и текущий угол поворота координатной оси от блока Integrator. Угол 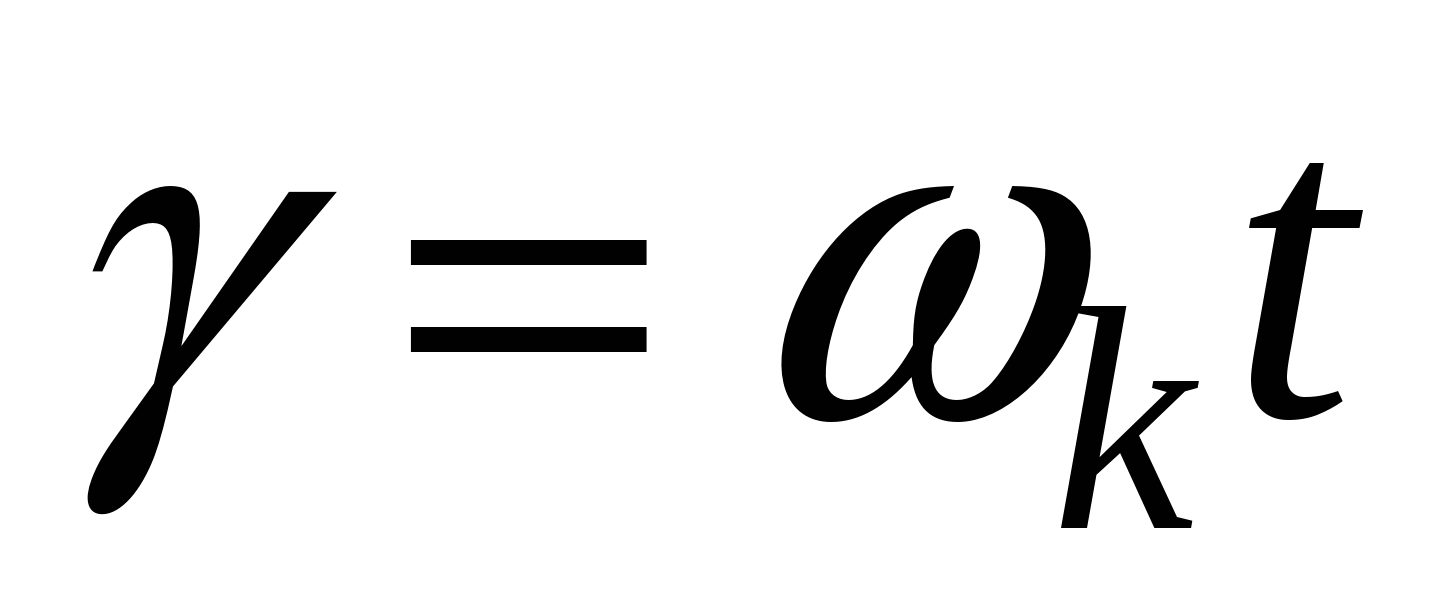 , где ωk представляет частоту вращения системы координат. Частота вращения в рад/сек задаётся константой на входе интегратора. Следует заметить, что в этом случае на вход модели подаются синусоидальные функции времени с частотой 314 рад/сек в неподвижной системе координат и задаётся вращение координат с частотой 314 рад/сек. Следовательно, на выходах Ux, Uy должны получиться неподвижные векторы, характеризуемые постоянными величинами на выходах Ux и Uy. Преобразователь координат реализован в блоке Subsystem, содержание которого представлено на рисунке 3.9. , где ωk представляет частоту вращения системы координат. Частота вращения в рад/сек задаётся константой на входе интегратора. Следует заметить, что в этом случае на вход модели подаются синусоидальные функции времени с частотой 314 рад/сек в неподвижной системе координат и задаётся вращение координат с частотой 314 рад/сек. Следовательно, на выходах Ux, Uy должны получиться неподвижные векторы, характеризуемые постоянными величинами на выходах Ux и Uy. Преобразователь координат реализован в блоке Subsystem, содержание которого представлено на рисунке 3.9.
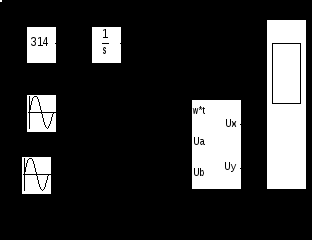 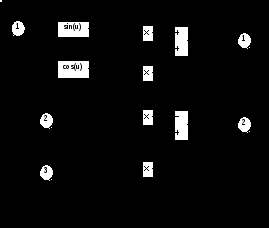
Рисунок 3.9 – Модель преобразователя из неподвижной системы координат во вращающуюся
На рисунке 3.10 представлены результаты моделирования. На экране осциллоскопа представлены синусоидальные напряжения Ua и Ub в неподвижной системе и постоянные напряжения Ux=0, Uy= –1 во вращающейся, подтверждающие предположение, сделанное выше.
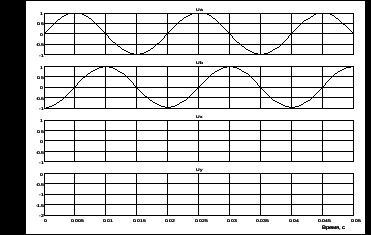
Рисунок 3.10 – Результаты моделирования
Если частоту вращения координат ωk задать отличной от частоты входного напряжения, то на выходе преобразователя появляются синусоидальные напряжения разностной частоты 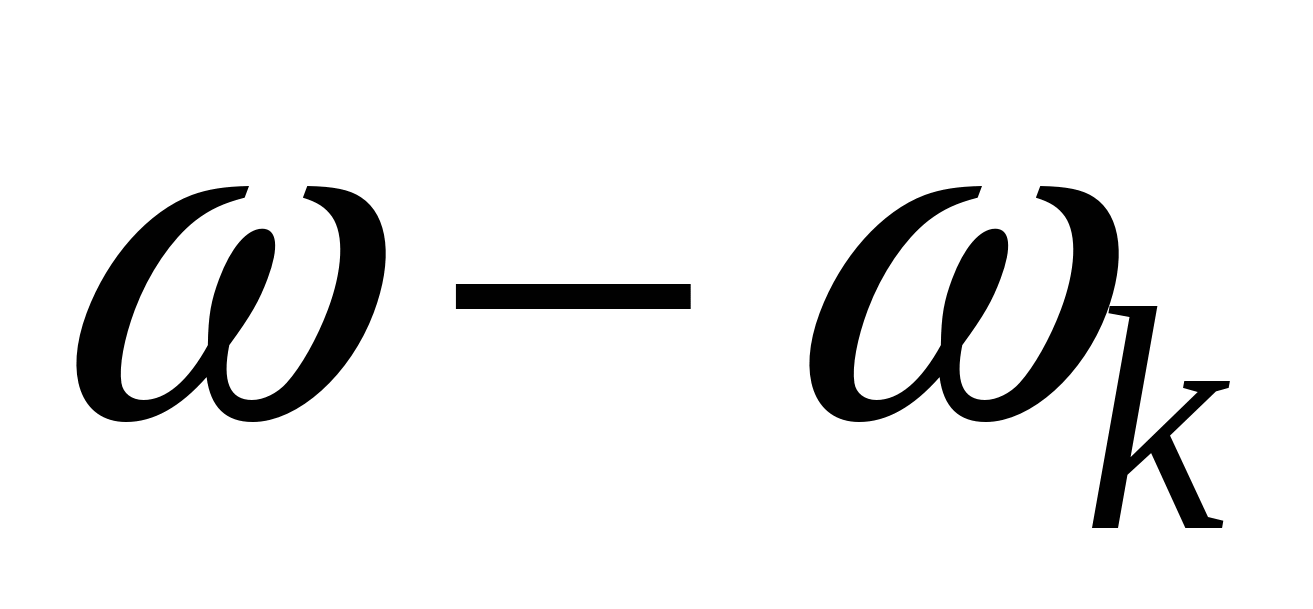 . Следовательно, пространственный вектор вращается во вращающейся системе координат с частотой . Следовательно, пространственный вектор вращается во вращающейся системе координат с частотой 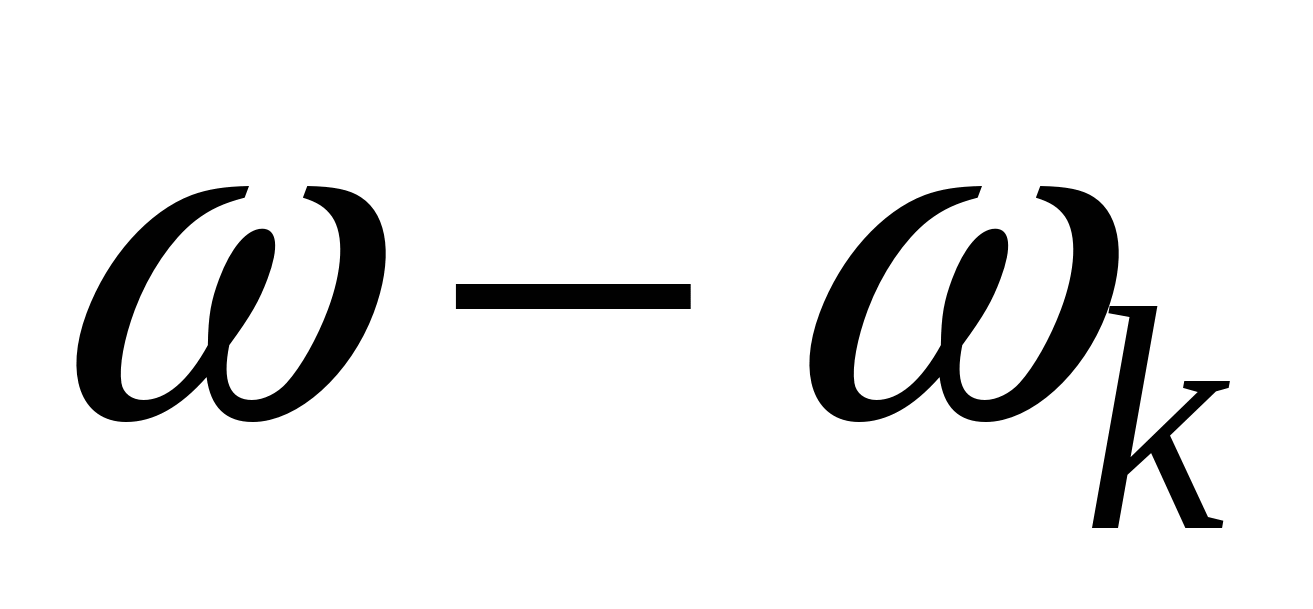 . .
Аналогичная модель строится и для преобразования переменных в вращающейся системе координат в неподвижную в соответствии с уравнениями (3.14) [2].
На рисунке 3.11 представлена модель преобразователя вращающейся системы координат в неподвижную, реализованную по уравнениям (3.14). На вход модели поданы проекции пространственного вектора напряжения на вращающиеся оси (х, у) и текущий угол поворота системы координат. На выходе модели получены составляющие пространственного вектора (Ua, Ub) в неподвижной системе координат. Преобразователь координат реализован в блоке Subsystem, содержание которого представлено на рисунке 3.11.
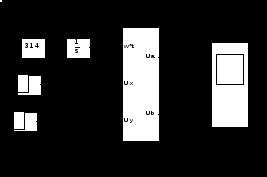 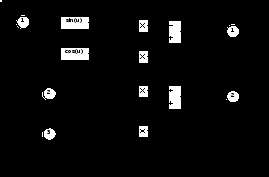
Рисунок 3.11 – Модель преобразователя вращающихся координат в неподвижные
На рисунке 3.12 представлены результаты моделирования. Напряжения Ua, Ubвидны на экране осциллоскопа. Следует заметить, что в этом случае на вход интегратора подаётся сигнал частоты вращения координат 314 !/с, и на выходе получаются синусоидальные напряжения частотой 50Гц.
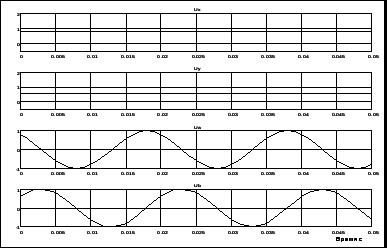
Рисунок 3.12 – Результат моделирования процесса преобразования вращающихся координат в неподвижные
3.2 Виртуальная модель асинхронного двигателя в среде MATLAB
По умолчанию модель асинхронного двигателя из раздела библиотеки SimPowerSystems даётся для фазного ротора (рисунок 3.13,а).
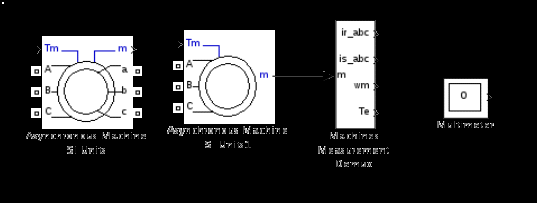
Рисунок 3.13 – Виртуальная модель асинхронной машины: а) модель в абсолютных единицах двигателя с фазным ротором; б) модель короткозамкнутого двигателя; в) измерительный инструмент
Клеммы A, B, C служат для подключения к трёхфазному напряжению, клеммы a, b, c – выходы обмотки ротора. Параметры двигателя для модификации SIUnits вводятся через диалоговое окно в абсолютных единицах, которое вызывается двойным щелчком по изображению двигателя (рисунок 3.14).
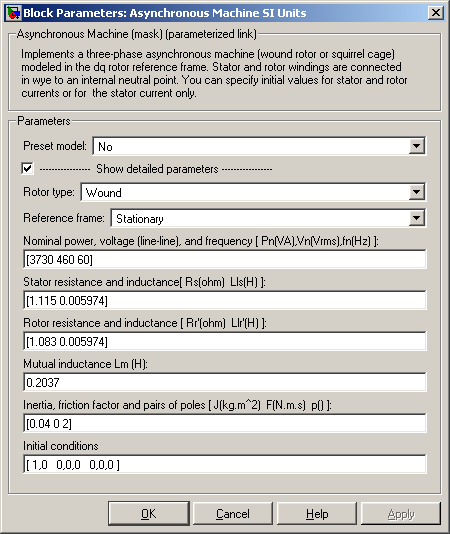
Рисунок 3.14 – Окно ввода параметров двигателя в абсолютных единицах
В строке Rotortype предлагается два варианта: Wound – двигатель с фазным ротором и Squirrel – cage – короткозамкнутый двигатель (с беличьей клеткой). В строке Referenceframe предлагается три варианта выбора системы координат:Rotor – вращающаяся с ротором с одинаковой частотой; Stationary – неподвижная, наиболее естественная для нас; Synchronous – система координат, синхронно вращающаяся с частотой сетевого напряжения. Параметры асинхронного двигателя вводятся в следующие строки в абсолютных единицах.
Чаще всего применяется короткозамкнутый двигатель (рисунок 3.13,б). К выходу m подключается специальный демультиплексор Machines Measurement Demux, находящийся в разделе SimPowerSystems в подразделе Machine.
Тип машины переменного тока отражается в строке Machinetype, открываемого двойным щелчком левой кнопки мыши (рисунок 3.15).
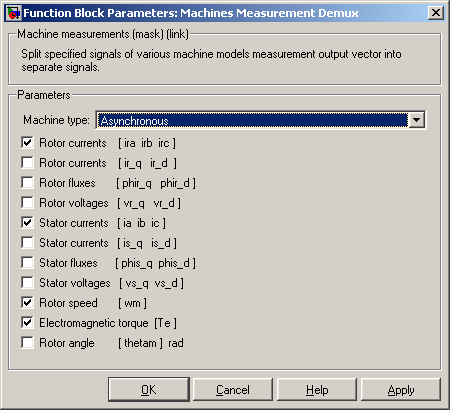
Рисунок 3.15 – Окно выбора типа машины и перечня выходных переменных
Следует иметь в виду, что эти параметры в справочниках и каталогах не приводятся, а рассчитываются с помощью различных методик, например, так, как это рассмотрено в предыдущем пункте.
По входу Tm задаётся активный момент нагрузки в Нм. По требованию программы Simulink на рабочем поле модели должен быть размещён блокMultimeter (рисунок 3.13, в), иначе процесс моделирования блокируется.
3.3 Математическое описание системы частотно – регулируемый
асинхронный электропривод – центробежный насос
Одним из наиболее эффективных путей развития энергосберегающих технологических режимов при управлении центробежными насосами является регулируемый электропривод. В настоящее время, доминирующее положение занимают частотно – регулируемые асинхронные электроприводы с системами автоматического управления, что позволяет решить не только технологические задачи насосных агрегатов, но и проблему энергосбережения [1].
Формирование требуемых статических и динамических свойств асинхронного частотно-регулируемого электропривода возможно лишь в замкнутой системе регулирования его координат, функциональная схема которого представлена на рисунке 3.16 [2].

Р – регулятор; Д – датчик переменных электропривода; ПЧ – преобразователь частоты.
Рисунок 3.16 – Функциональная схема замкнутой системы ПЧ-АД.
Для увеличения диапазона регулирования по скорости в данную систему регулирования необходимо введение отрицательной обратной связи по скорости. Поэтому в математическом описании переходных процессов электропривода учитывается обратная связь по скорости. Структурная схема системы ПЧ-АД с отрицательной обратной связью по скорости будет иметь вид [2]:
Отметим, что структурная схема, в соответствии с рисунком 3.17,
является линеаризованной системой электропривода.

Рисунок 3.17 – Структурная схема системы ПЧ-АД с обратной связью по скорости.
На схеме приняты следующие обозначения:
β – модуль жесткости механической характеристики ;
Тэ – эквивалентная электромагнитная постоянная времени цепей статора и ротора АД;
kПЧ – передаточный коэффициент функции ПЧ;
ТПЧ – постоянная времени цепи управления ПЧ;
Тм – электромеханическая постоянная времени.
Уравнение движения, согласно передаточной функции W1 структурной
схемы, можно записать в следующем виде:
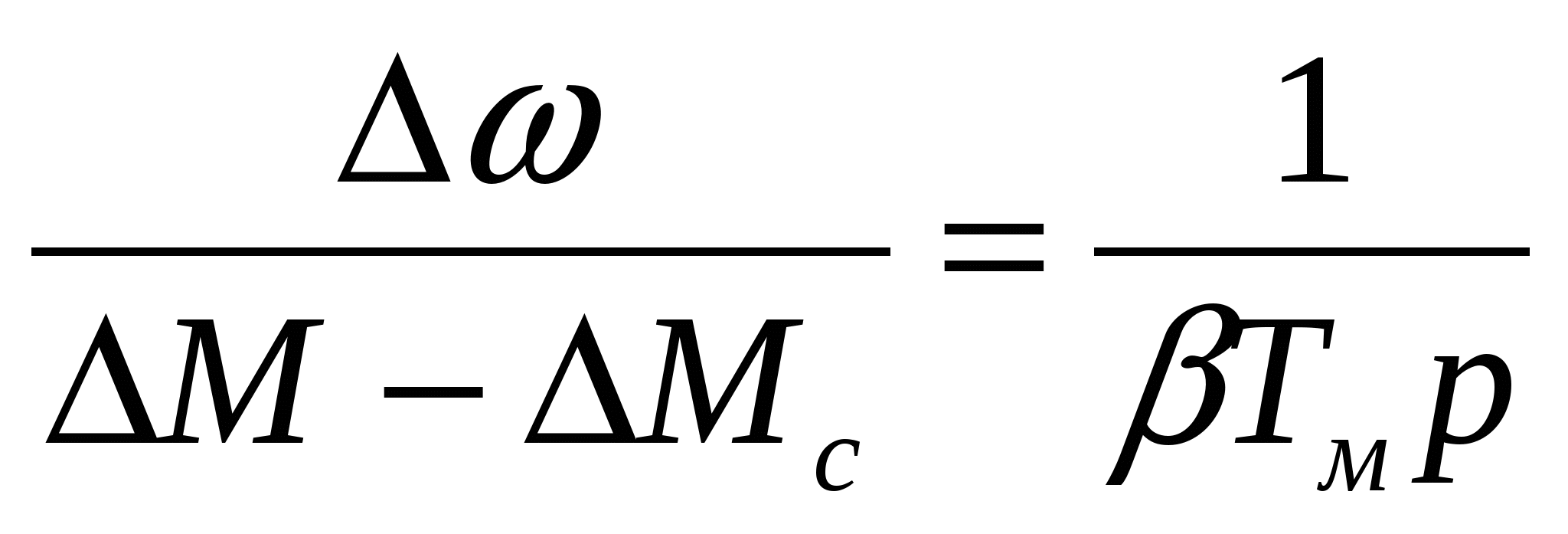 , (3.15) , (3.15)
или
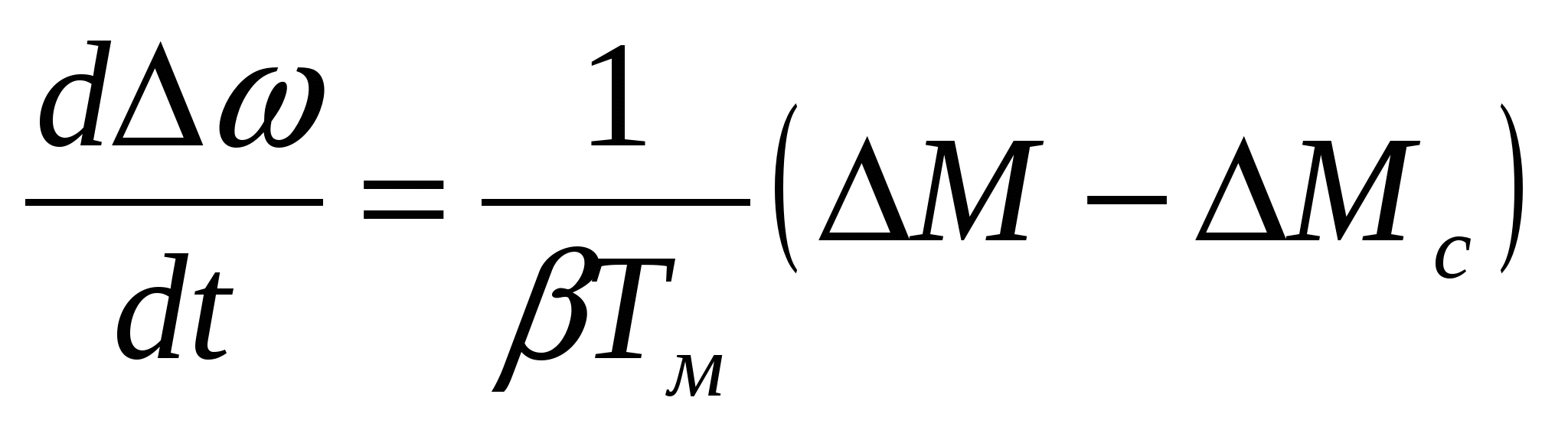 , (3.16) , (3.16)
где 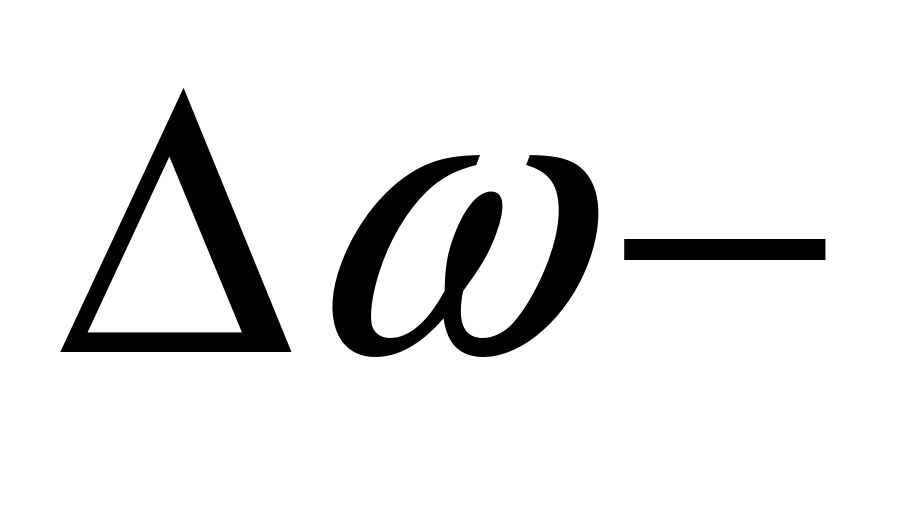 приращение скорости; приращение скорости; 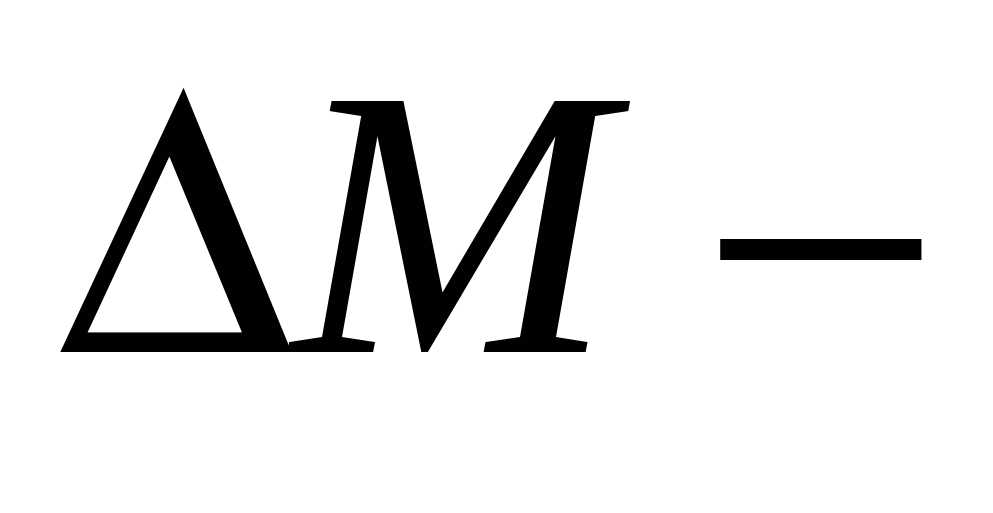 приращение момента; приращение момента;
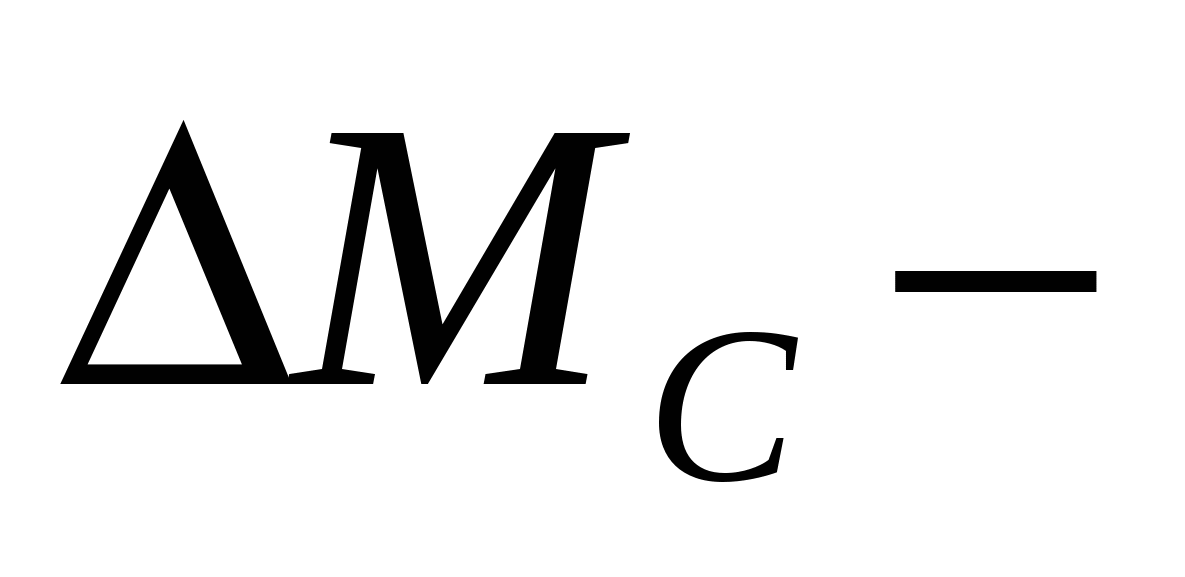 приращение статического момента нагрузки. приращение статического момента нагрузки.
Согласно передаточной функции W2 будем иметь следующее
соотношение:
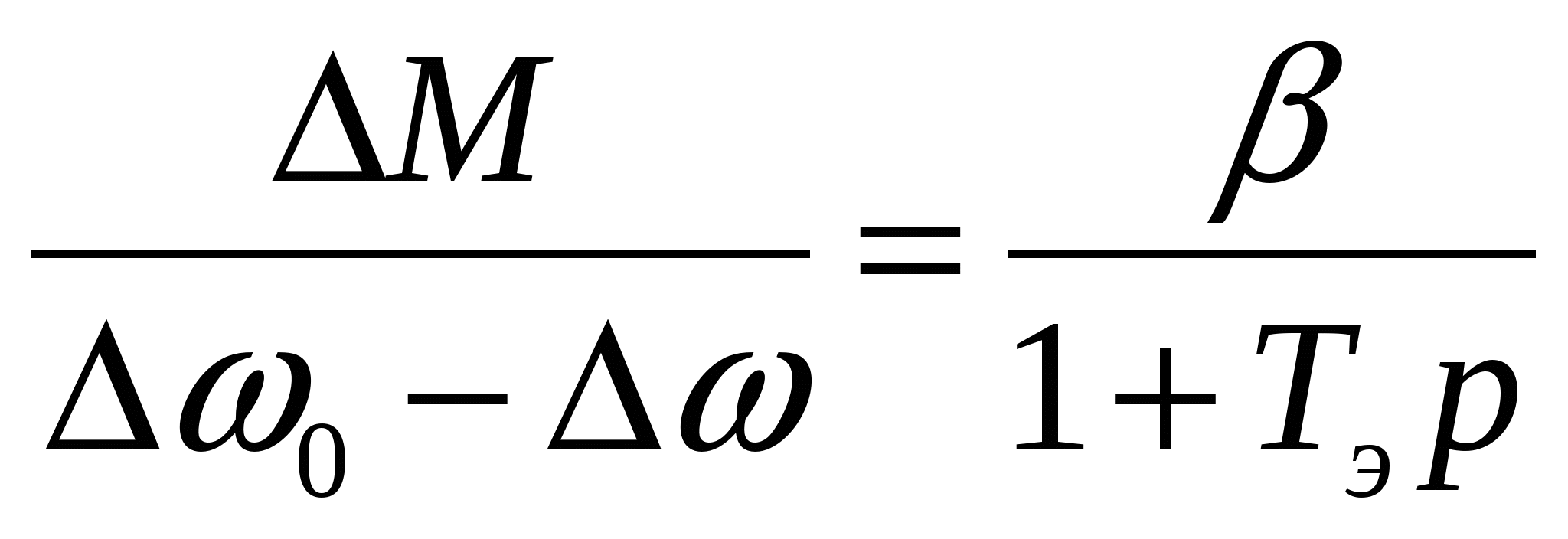 , (3.17) , (3.17)
которое можно написать в виде дифференциального уравнения:
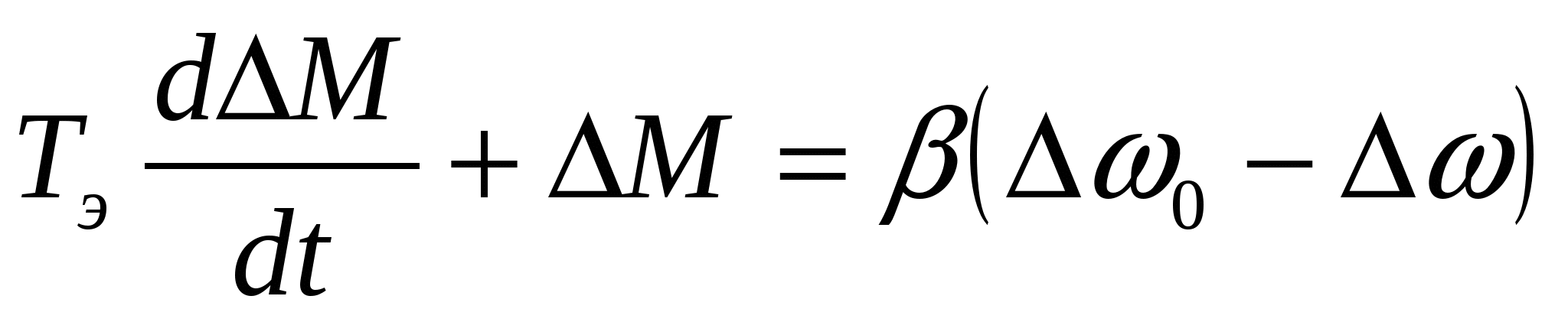 , (3.18) , (3.18)
где 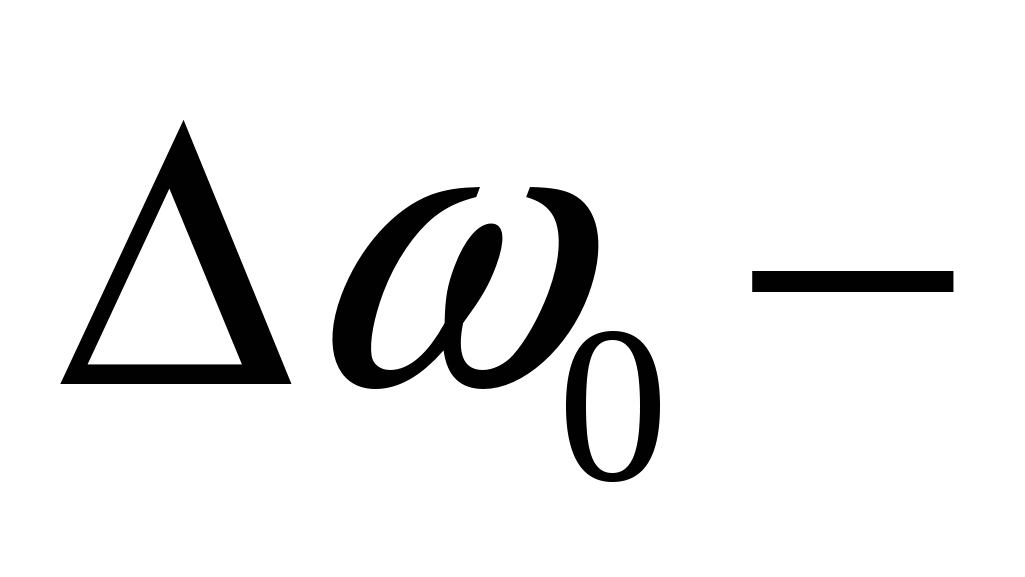 приращение угловой скорости электромагнитного поля АД. приращение угловой скорости электромагнитного поля АД.
Уравнение ПЧ, исходя из передаточной функции W3, запишем:
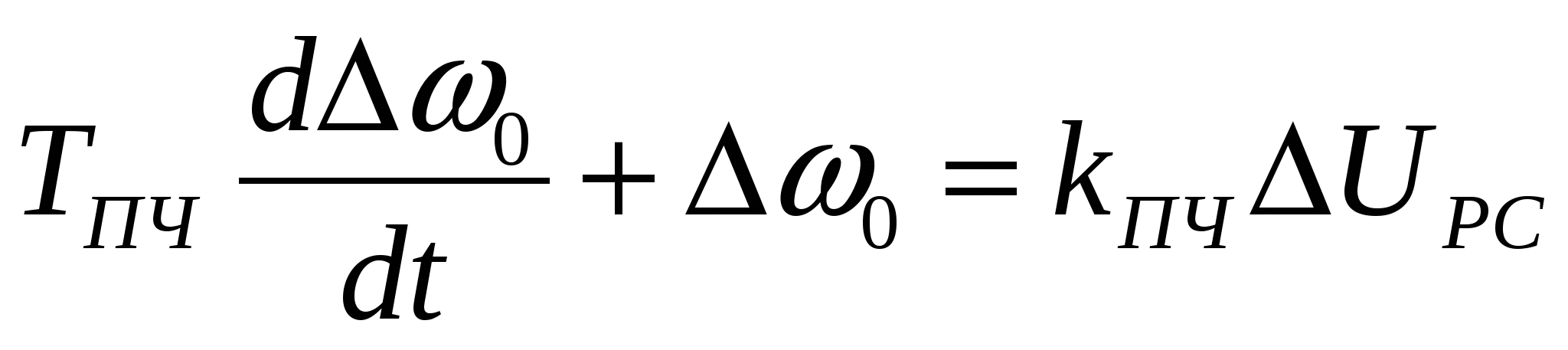 , (3.19) , (3.19)
а РС ( передаточная функция W4) представим уравнением:
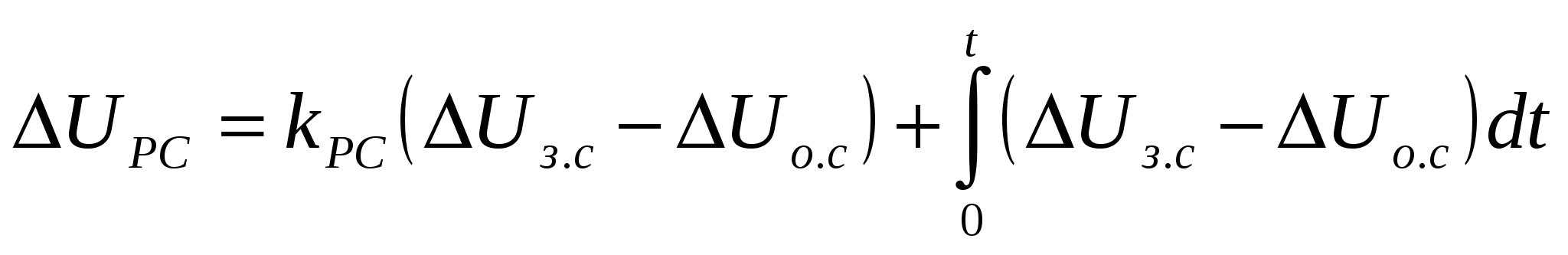 , (3.20) , (3.20)
или
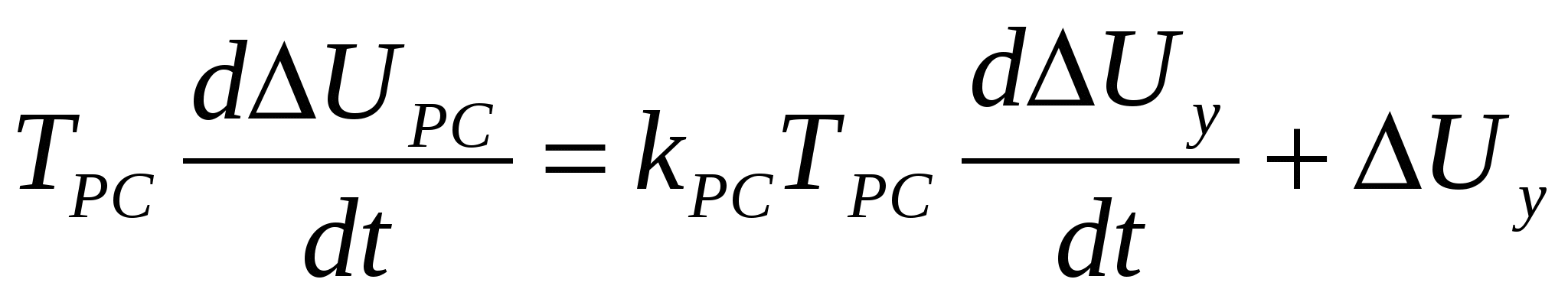 , (3.21) , (3.21)
Приращение 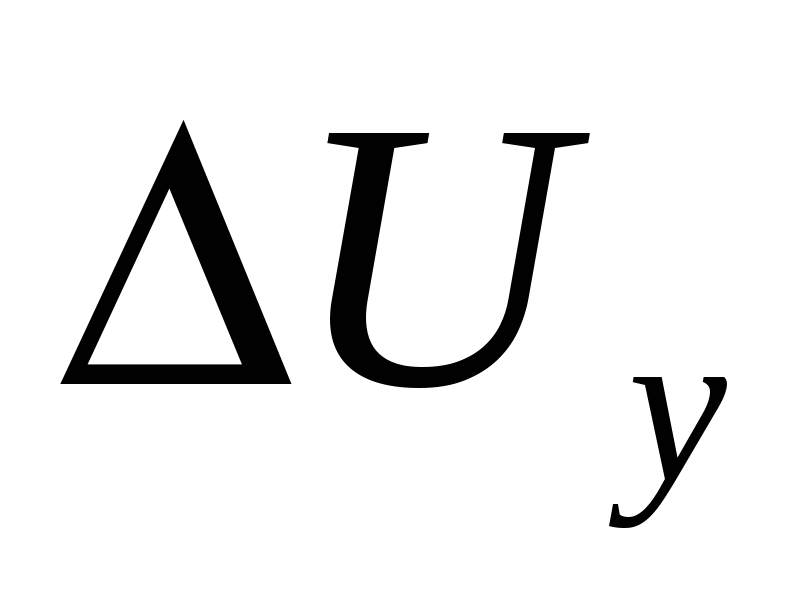 запишем в следующем виде: запишем в следующем виде:
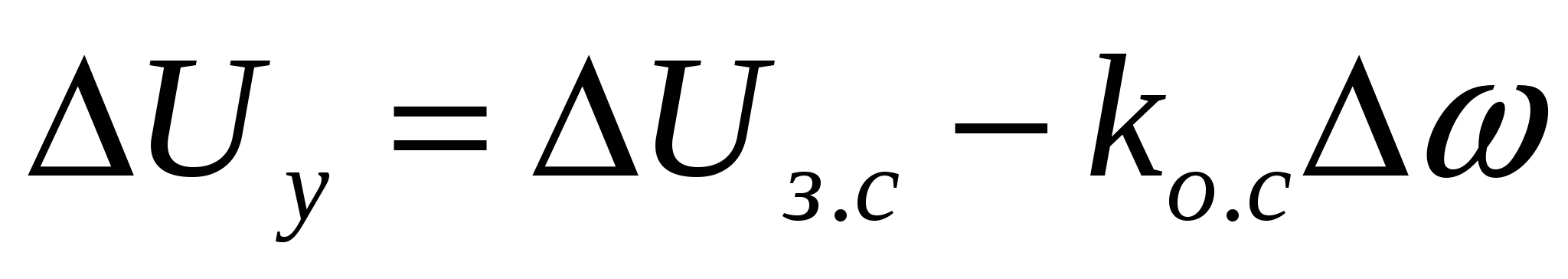 , (3.22) , (3.22)
где 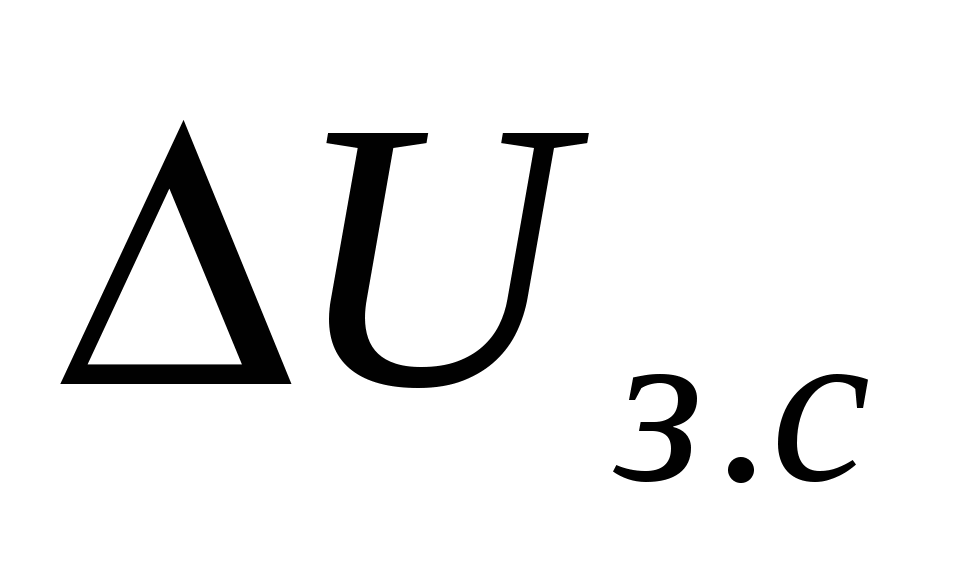 - приращение задающего сигнала; - приращение задающего сигнала;
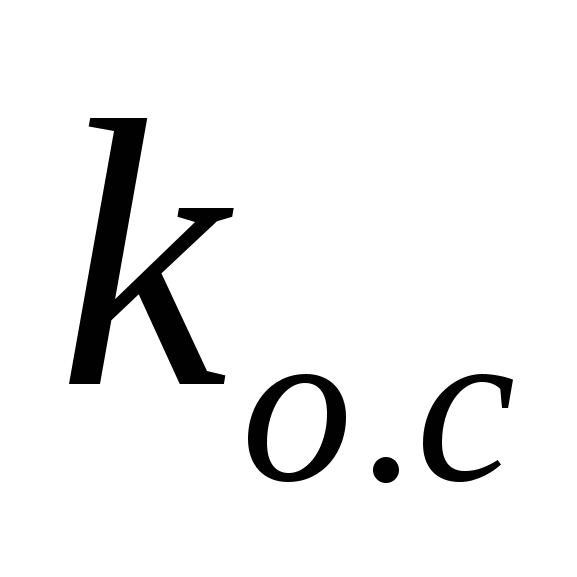 - коэффициент обратной связи по скорости. - коэффициент обратной связи по скорости.
Таким образом, математическое описание частотно – регулируемого
электропривода центробежного насоса можно представить следующей
системой уравнений:
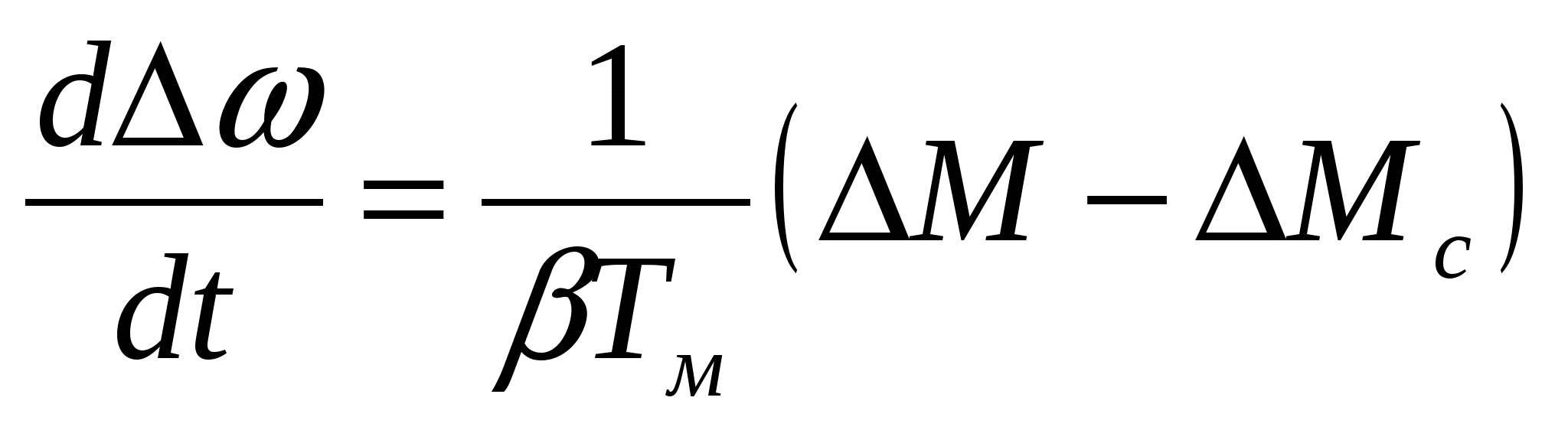 , ,
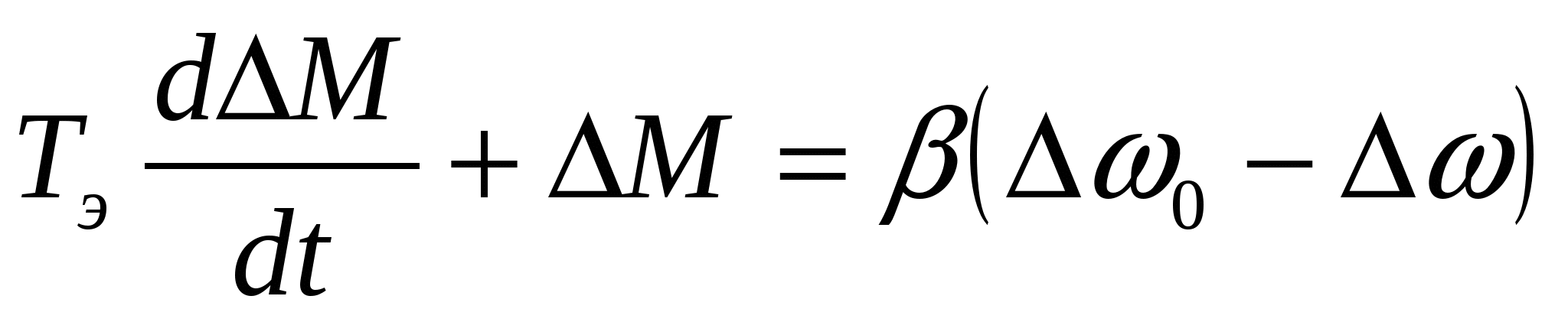 , (3.23) , (3.23)
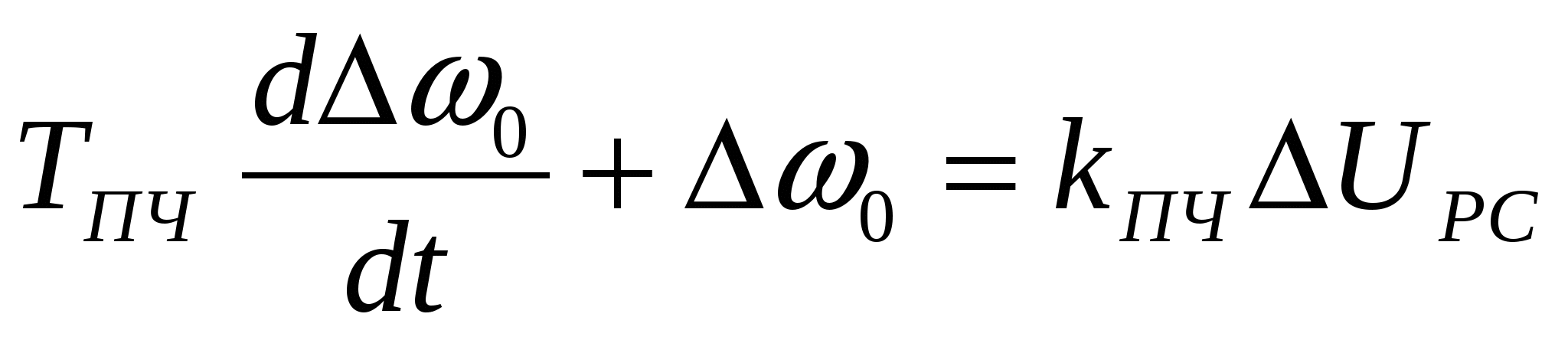 , ,
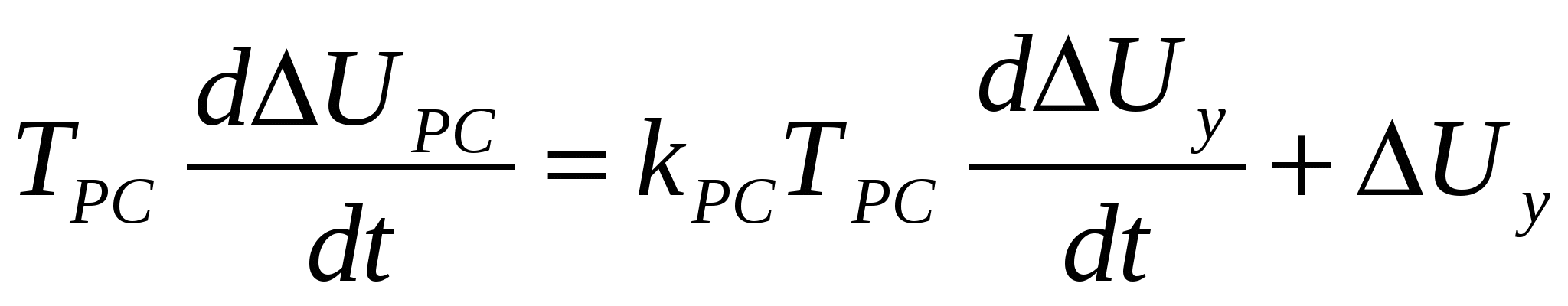 , ,
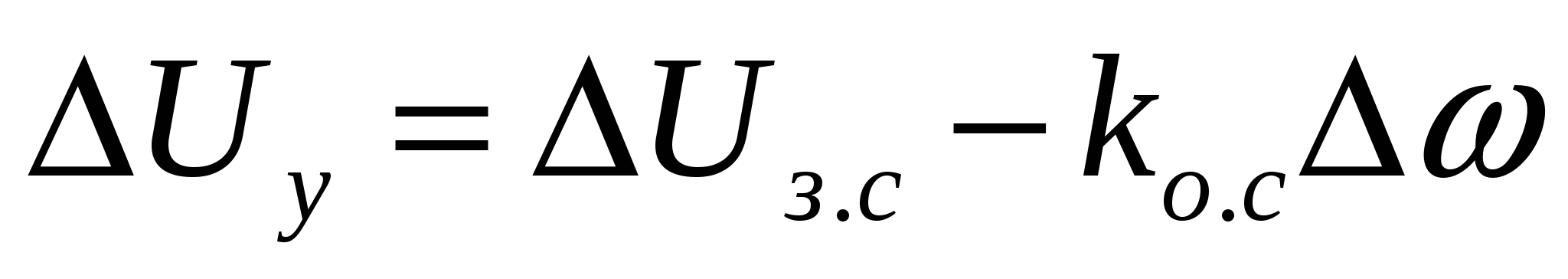 . .
3.4 Математическая модель центробежного насоса
Рассмотрим центробежный насос как объект управления и приведем математическое описание его статических и динамических режимов на основе математической модели центробежного насоса [3].
Математическое описание напорнорасходной характеристики насоса
запишется в следующем виде:
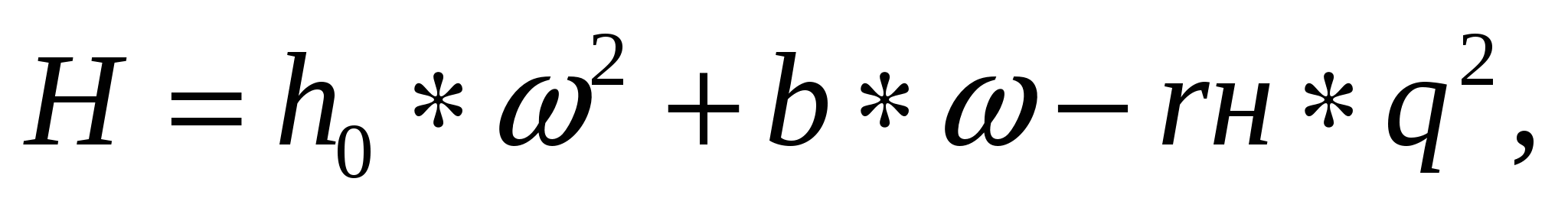 (3.24) (3.24)
где h0 – приведенный напор холостого хода насоса;
b – коэффициент, характеризующий линейную зависимость между напором и подачей насоса;
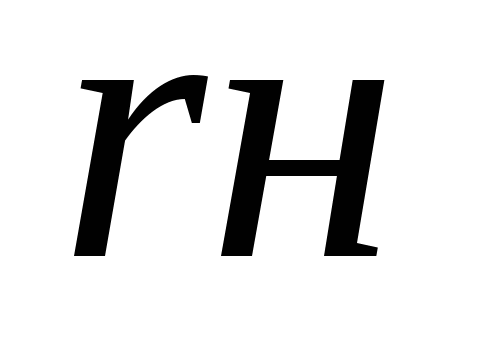 - коэффициент, характеризующий внутреннее гидравлическое - коэффициент, характеризующий внутреннее гидравлическое
сопротивление насоса.
В уравнении (3.24) два первых члена определяют процесс передачи
энергии от рабочего колеса жидкости, а третий член определяет суммарные потери центробежного насоса, пропорциональные квадрату производительности. Из этого следует, что динамические показатели и инерционность насоса определяется двумя первыми слагаемыми уравнения (3.10). Для получения зависимостей, характеризующих поведение насоса в динамике, обозначим 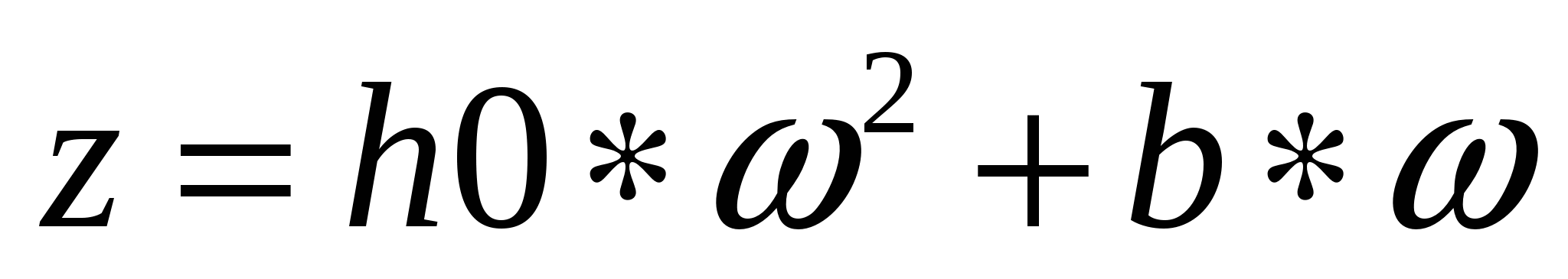 как динамическую составляющую характеристику центробежного насоса. как динамическую составляющую характеристику центробежного насоса.
Динамическую характеристику насоса с учетом переходных процессов в нем можно представить в виде:
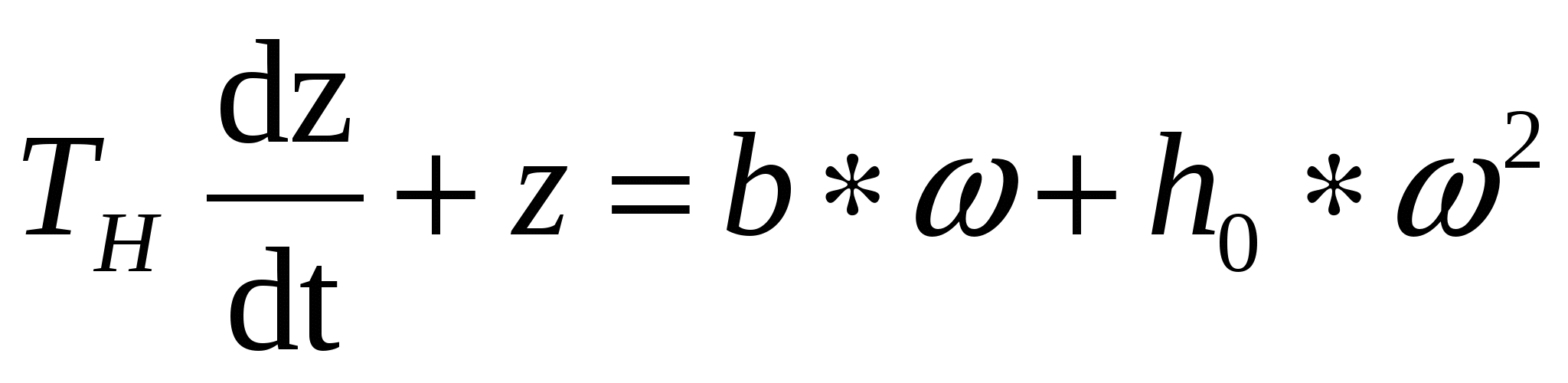 , (3.25) , (3.25)
или
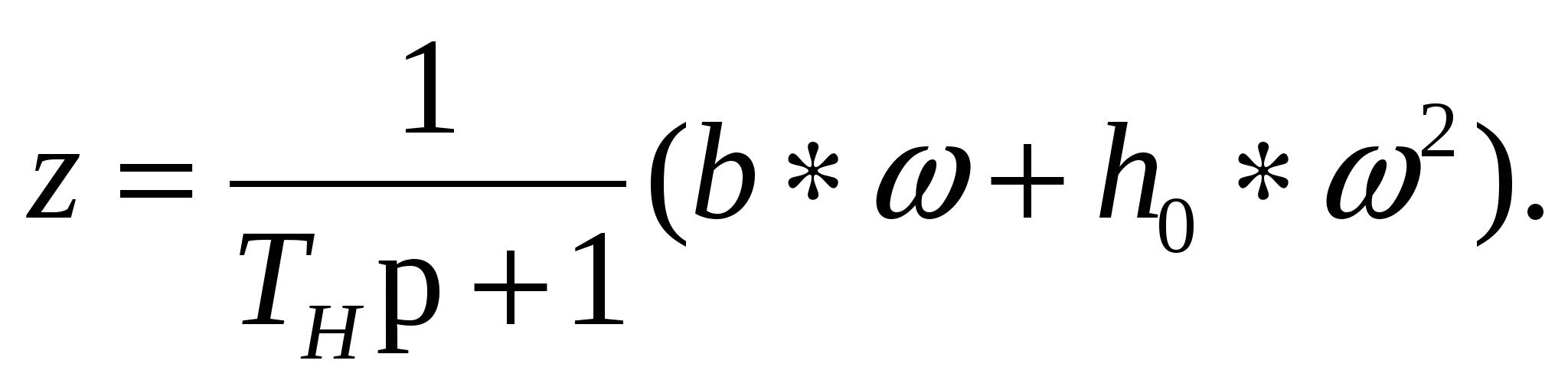 (3.26) (3.26)
Следует отметить, что насос с системой ПЧ – АД с обратной связью по скорости представляют единый механизм, который обладает маховой массой, составленной ротором электродвигателя и рабочим колесом насоса и имеет механическую постоянную времени.
3.5 Моделирование системы ПЧ – АД – центробежный насос в MATLAB
Математическая модель системы ПЧ – АД с обратной связью по скорости – центробежный насос, на основе системы уравнений (3.23) и (3.25), будет иметь следующий вид:
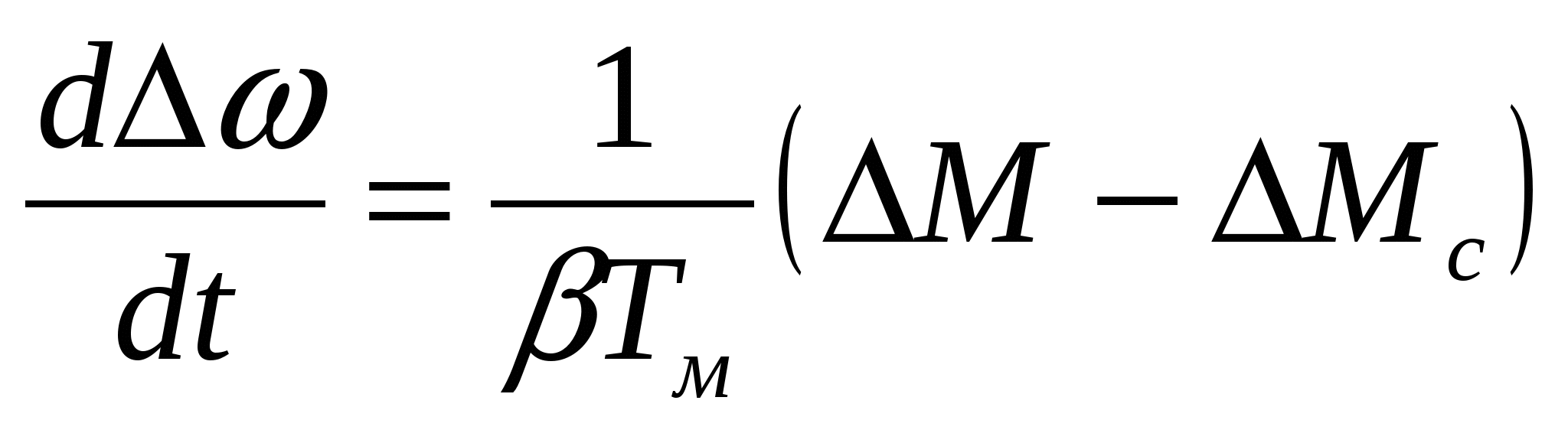 , ,
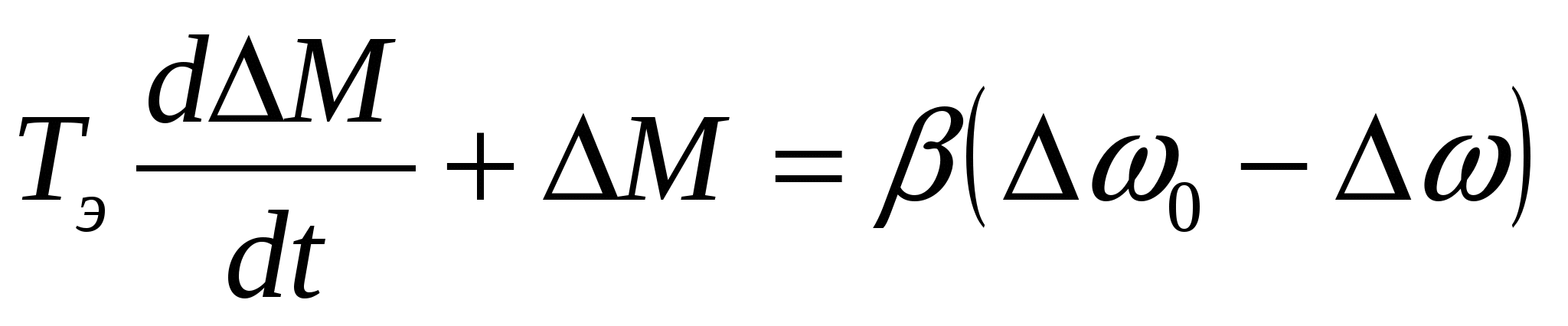 , ,
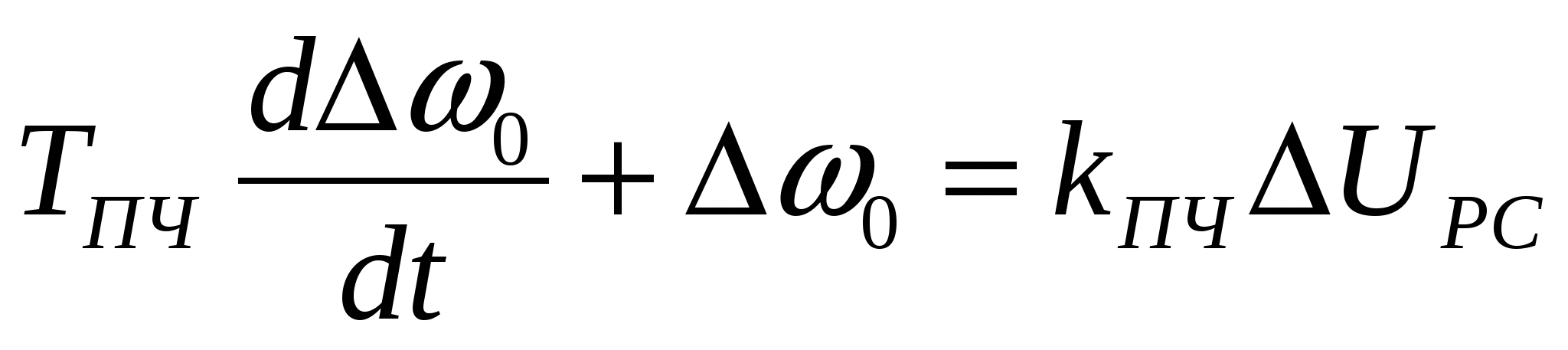 , (3.27) , (3.27)
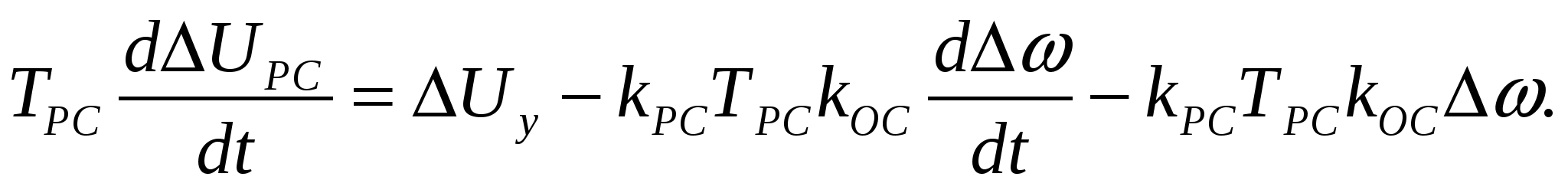

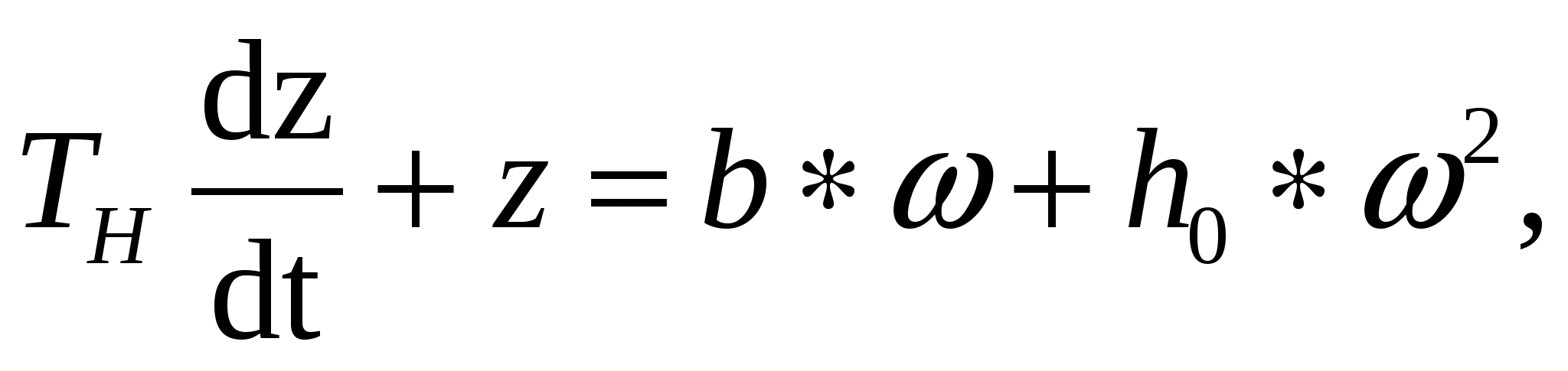
где 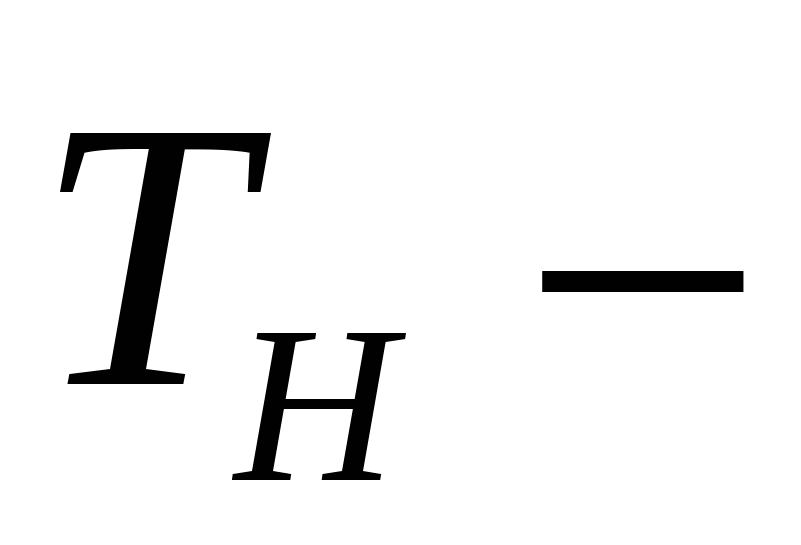 постоянная времени переходных процессов в рабочем колесе насоса (аналогична электромагнитной постоянной времени электродвигателя). постоянная времени переходных процессов в рабочем колесе насоса (аналогична электромагнитной постоянной времени электродвигателя).
Для удобства исследования переходных процессов динамики
системы ПЧ – АД с обратной связью по скорости и центробежный насос, после несложных преобразований, систему уравнений (3.13) представим в следующем виде:
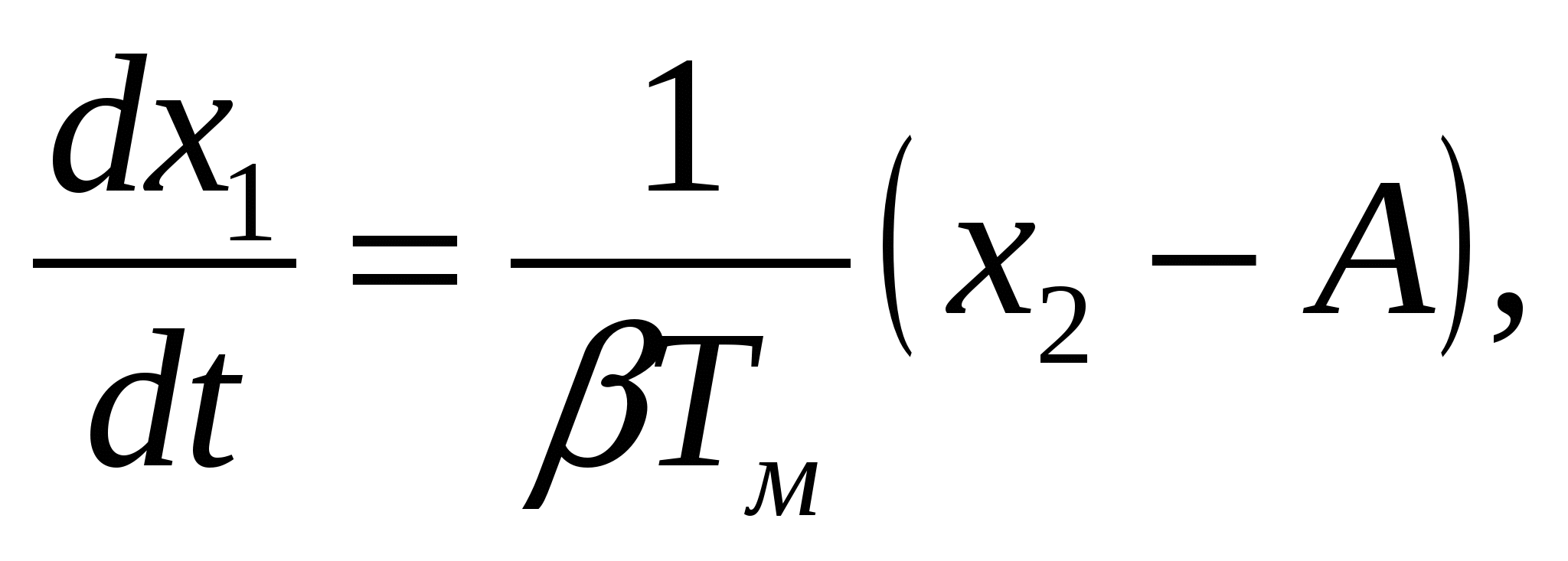
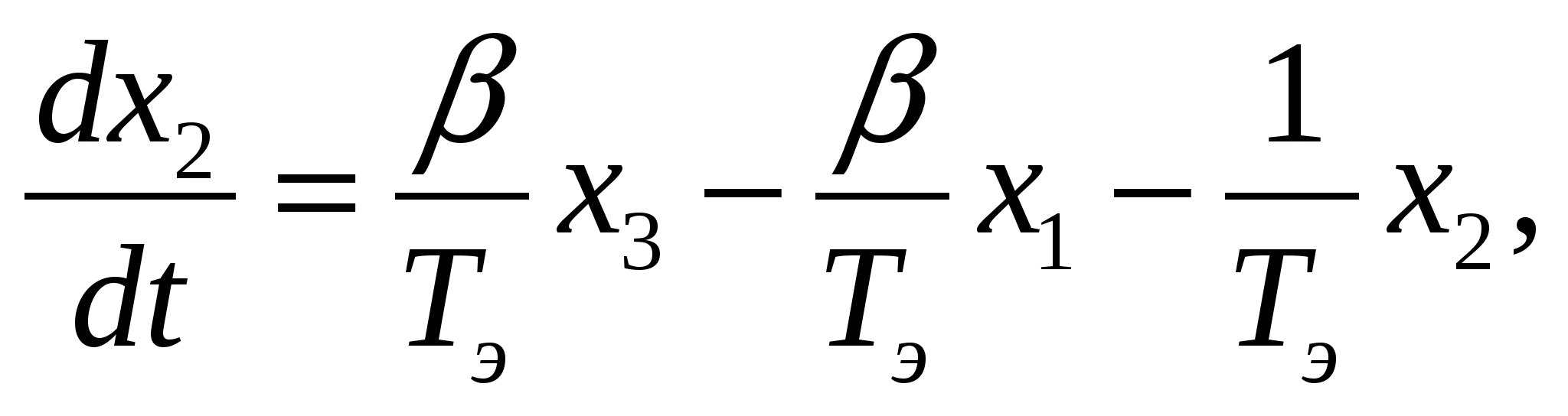
(3.28)
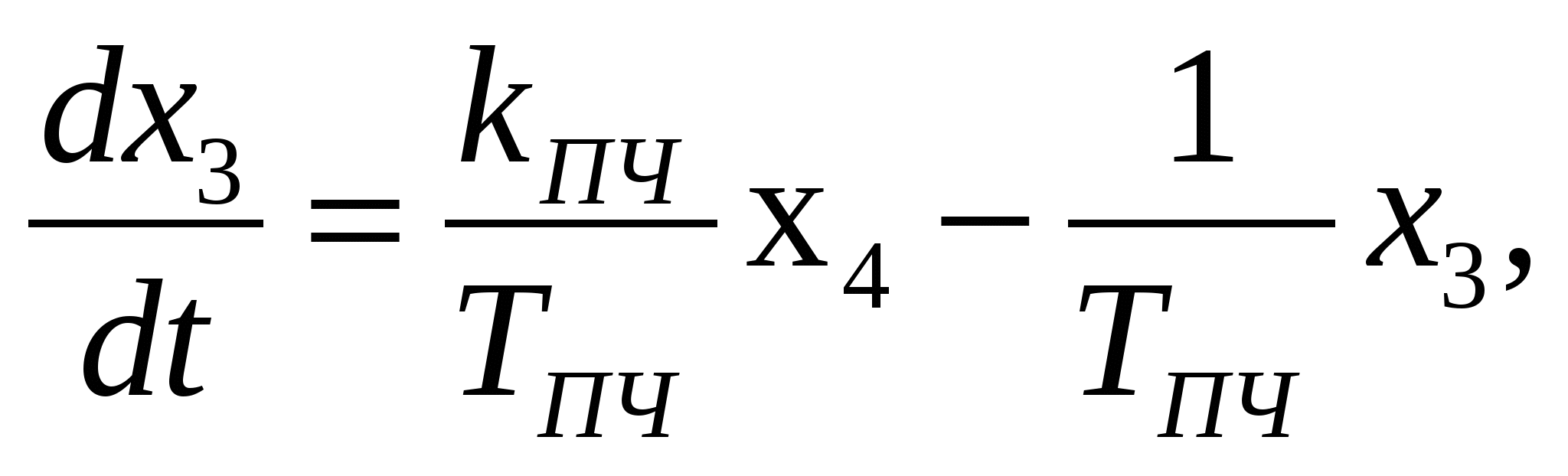
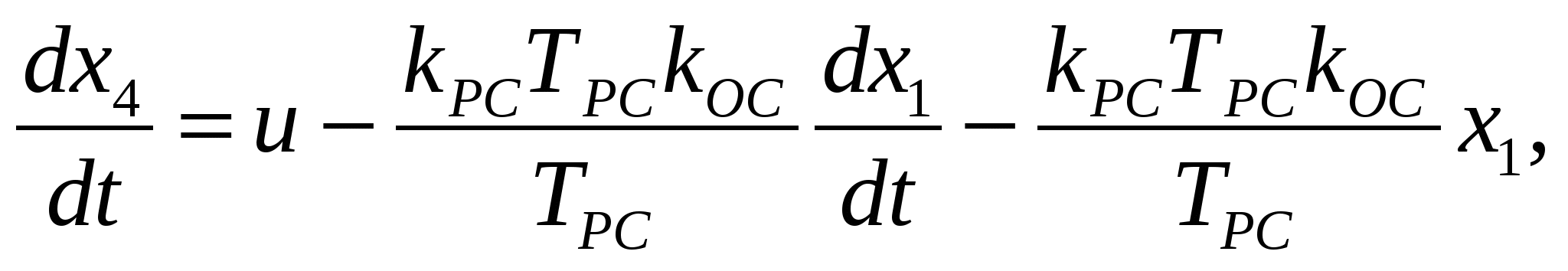
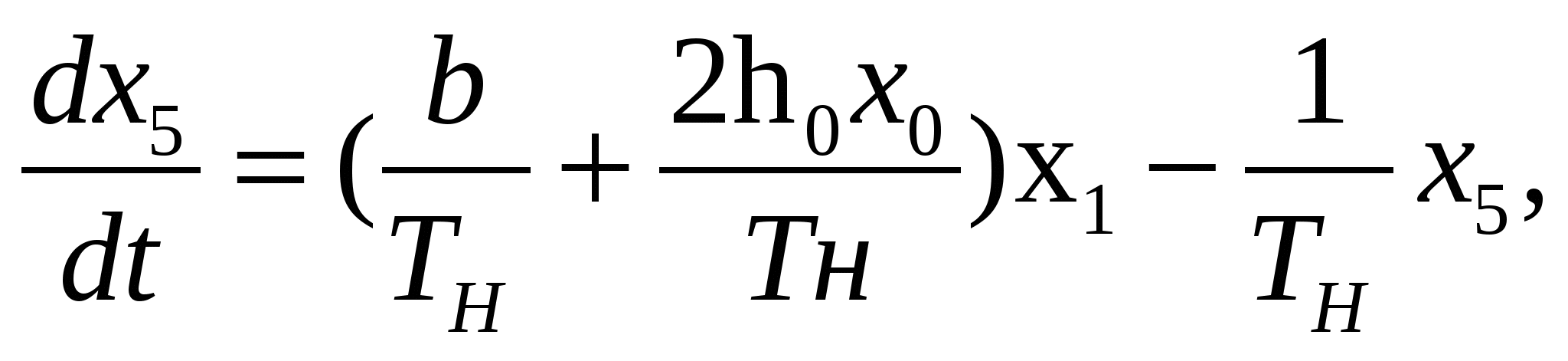 
где 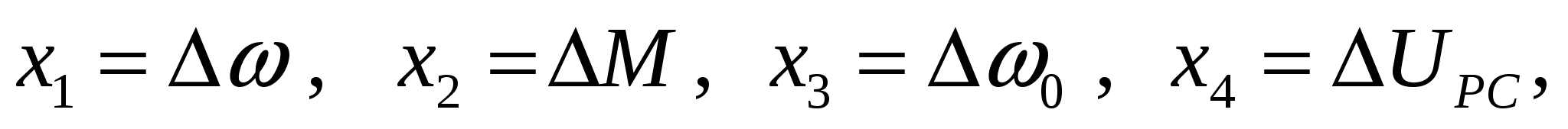 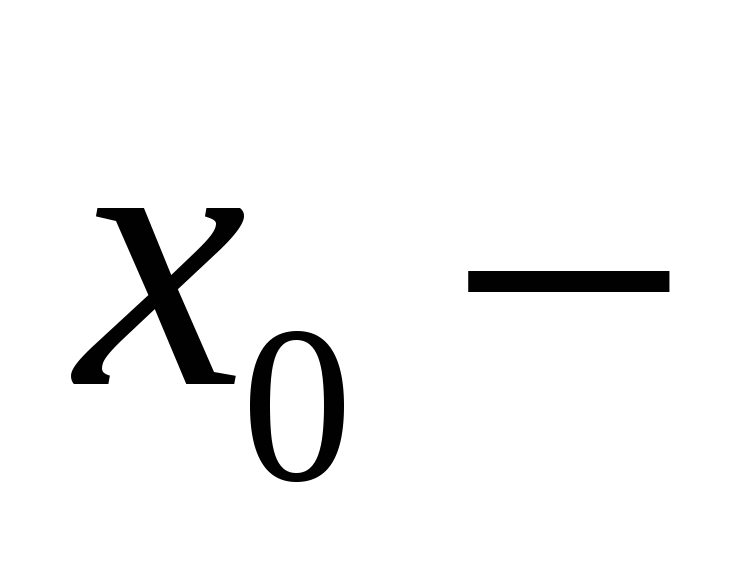 коэффициент линеаризации коэффициент линеаризации
переменной 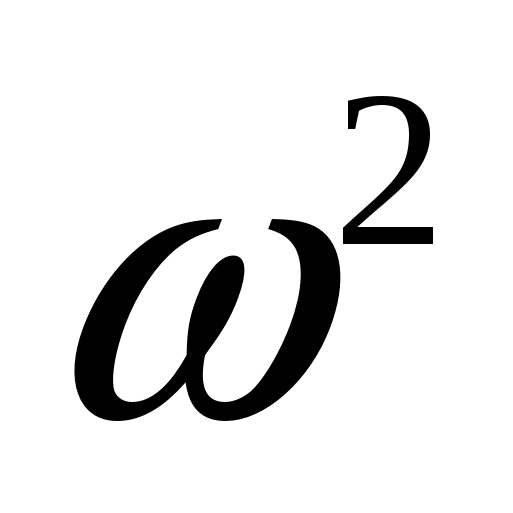 . .
Программа решения системы (3.28), при параметрах асинхронного двигателя 4А112М2У3:

параметрах ПЧ:
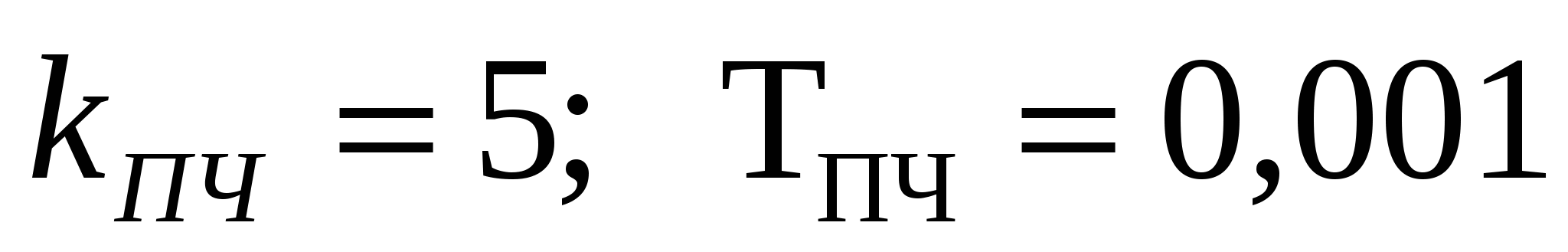 , ,
параметрах регулятора скорости, коэффициента обратной связи:
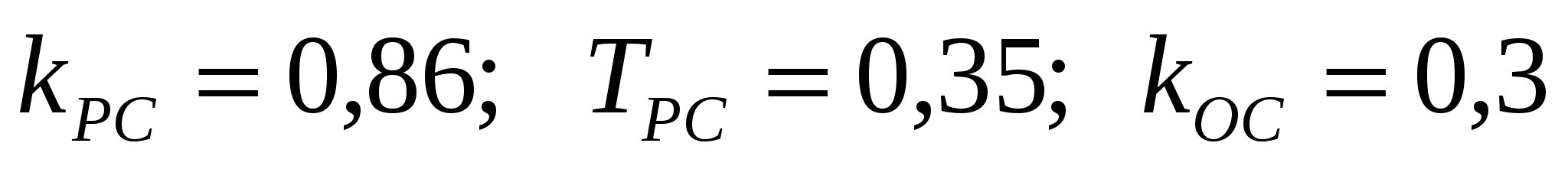 , ,
а также параметрах центробежного насоса К90/20:
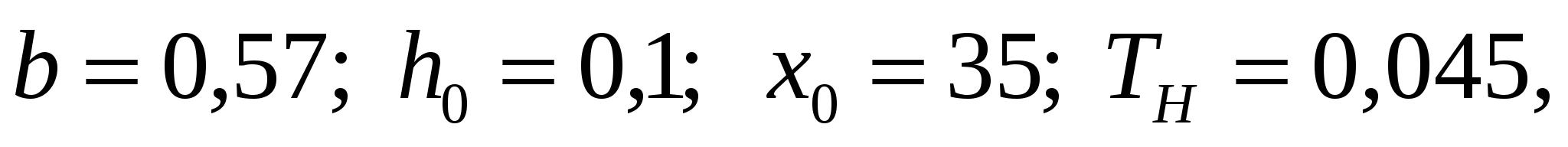
представлена на рисунке 3.18:
function MMN
x0=[0;0;0;0;0];
[T,X]=ode45(@nass,[0 20],x0);
plot(T,X(:,1),'g-');
%plot(T,X(:,5),'k-');
hold on
grid
hold off
function dx=nass(t,x)
dx=zeros(5,1);
dx(1)=1.96*x(2)-78.6*x(1);
dx(2)=101.7*x(3)-101.7*x(1)-20*x(2);
dx(3)=5000*x(4)-1000*x(3);
dx(4)=5*(1-exp(-t/3))-0.74*(1.96*x(2)+0.56*x(1)-
80*x(1)^2)- 0.74*x(1);
dx(5)=140*x(1)-20*x(5);
end
end
Рисунок 3.18 - программа решения системы, при параметрах асинхронного двигателя 4А112М2У3
Динамика системы ПЧ – АД – Центробежный насос может быть исследована на структурной схеме модели представленной на рисунке 3.19.
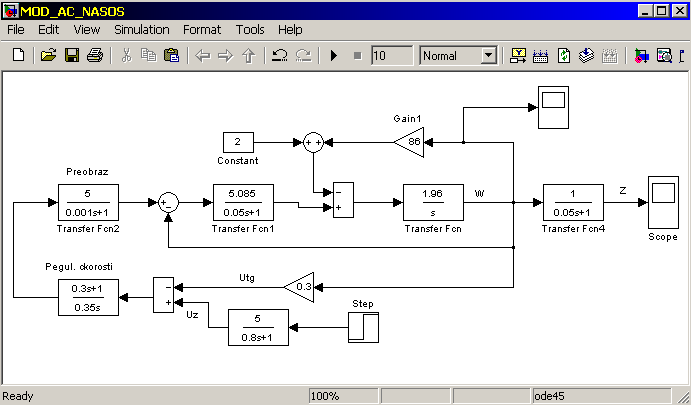
Рисунок 3.19 - Структурная схема модели системы ПЧ – АД – ЦБН
в MATLAB
В программе, для решения системы дифференциальных уравнений (3.28) используется численный метод Рунге – Кутта [4].
Осциллограммы, полученные в результате моделирования, приведены на рисунках 3.20, 3.21. На рисунке 3.20 представлен переходной процесс
скорости системы ПЧ – АД, на рисунке 3.21 представлен переходной процесс давления на выходе насоса.
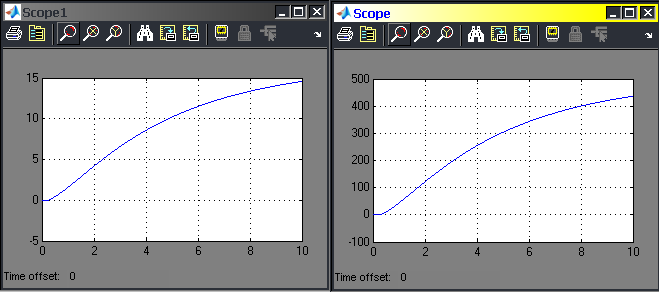
Рисунок 3.20 Рисунок 3.21
На рисунках 3.22, 3.23 показаны переходные процессы системы ПЧ – АД и ЦБН при изменении параметров регулятора скорости ПЧ – АД (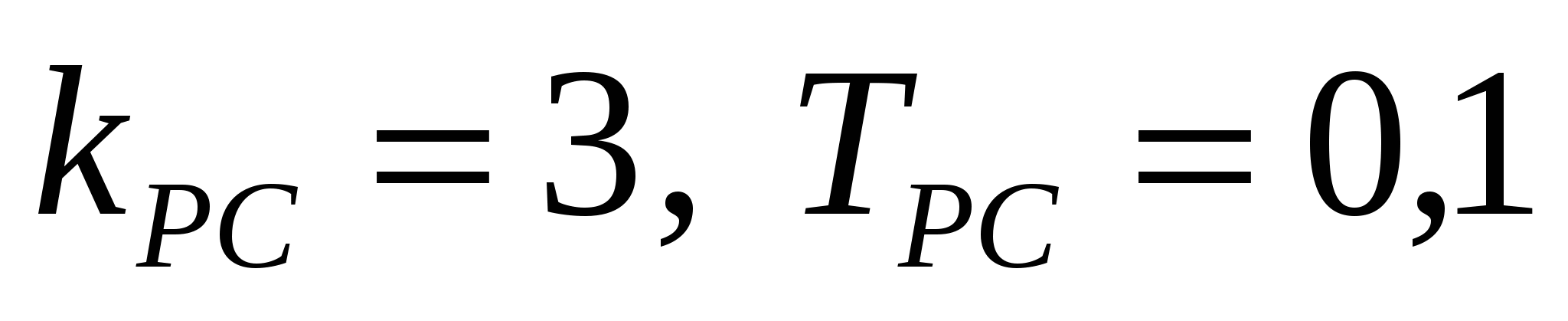 ). ).
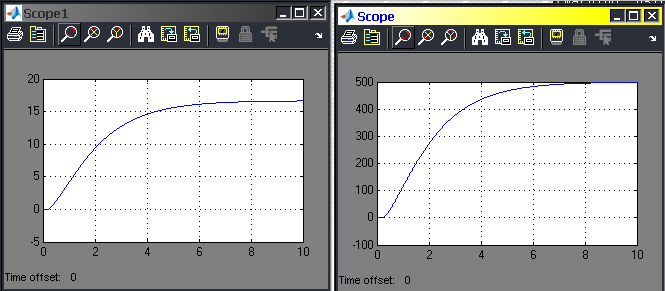
Рисунок 3.22 Рисунок 3.23
Визуальное исследование осциллограмм (рисунок 3.22, 3.23) показывает, что скорость вращения колеса насоса по качественным характеристикам соответствует скорости системы ПЧ – АД с обратной связью по скорости. Визуальное исследование осциллограмм (рисунок 3.24, 3.25) показывает, что темп нарастания давления (ускорение) выше, чем темп нарастания скорости системы ПЧ-АД.
|
|
|
 Скачать 1.8 Mb.
Скачать 1.8 Mb.

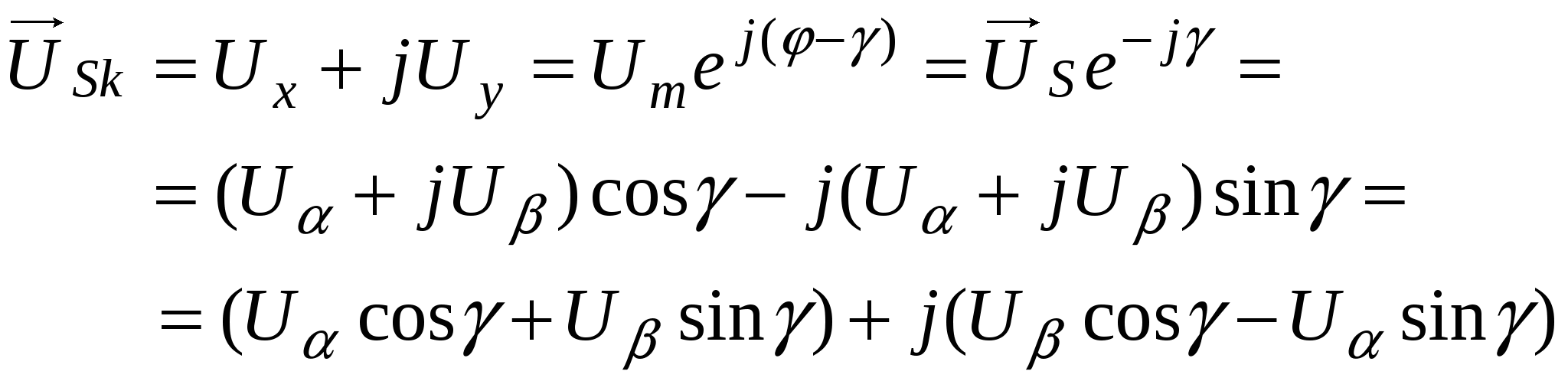 , (3.12)
, (3.12)












