синус косинус примеры. Дан треугольник. Радиус его описанной окружности. Угол, а может быть острым, тупым или прямым. Рассмотрим эти случаи отдельно
 Скачать 92.69 Kb.
|
|
Дан треугольник АВС, ВС = 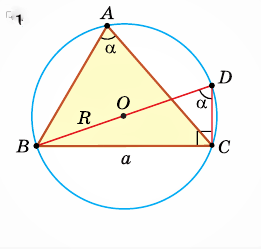  — радиус его описанной окружности. Угол, а может быть острым, тупым или прямым. Рассмотрим эти случаи отдельно. Угол  острый. Проведя диаметр BD и отрезок DC, получим прямоугольный треугольник BCD, в котором  как вписанный угол, опирающийся на диаметр. Заметим, что  как вписанные углы, опирающиеся на одну и ту же дугу ВС. Из прямоугольного треугольника BCD находим  т.е.  откуда  Доказать справедливость формулы площади треугольника 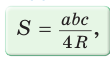 где  — его стороны, R — радиус описанной окружности.Доказательство: Воспользуемся известной формулой площади треугольника: 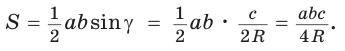 По теореме синусов  откуда  Тогда  Что и требовалось доказать. В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB 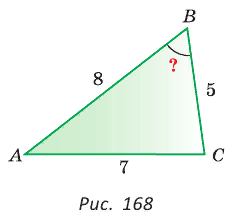 По теореме косинусов  Используя записанную выше формулу, можно сразу получить: 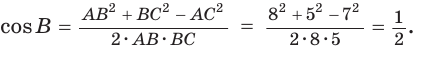 |