Расчет цифрового фильтра
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
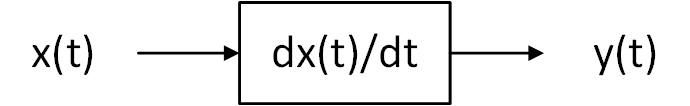 Рисунок 1 – Схема преобразования входного воздействия в выходное с помощью дифференцирующего фильтра Непрерывный дифференцирующий фильтр реализует математическую операцию 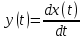 , где , гдеx(t) – непрерывный входной сигнал. Выходной сигнал идеального дифференцирующего фильтра равен первой производной от входного сигнала. Частотная передаточная функция идеального дифференциатора имеет вид 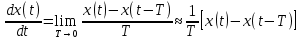 , где , где T – время задержки сигнала x(t), x(t) – текущее значение дифференцирующего сигнала, x(t-T) – задержанное на время T значение дифференцирующего сигнала. Структура устройства, реализующего данную операцию, показано на рисунке 25. 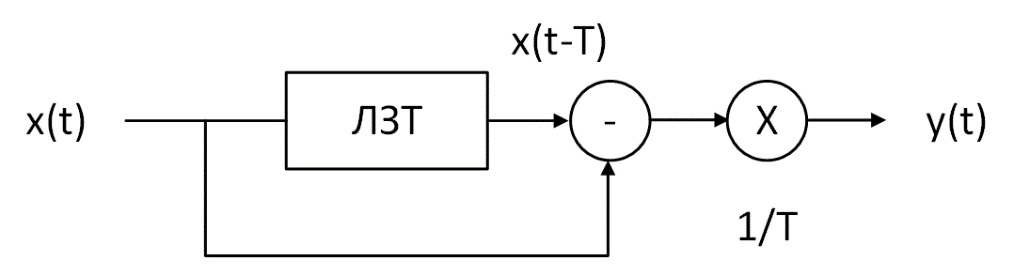 Рисунок 2 – Структурная схема дифференцирующего фильтра Частотная передаточная функция дифференциатора может быть записана в виде  . .Согласно формуле Эйлера 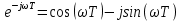 , ,Тогда частотная передаточная функция идеального дифференцирующего фильтра будет определяться как 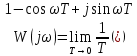 . .В пределе при T → 0; ωT → 0, cosωT ≈ 1 -  , а sinωT ≈ ωT. Таким образом получаем выражение , а sinωT ≈ ωT. Таким образом получаем выражение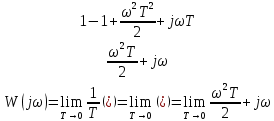 . .Поскольку  → 0, частотная передаточная функция для идеального дифференциатора записываются следующим образом → 0, частотная передаточная функция для идеального дифференциатора записываются следующим образом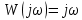 . .Амплитудно-частотная характеристика идеального дифференцирующего фильтра определяется, как 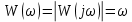 . .Для перехода от непрерывного дифференцирующего фильтра к цифровому фильтру необходимо воспользоваться выражением 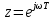 . .Из данного выражения находим, что  или или 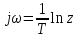 , где , гдеT – период дискретизации или период следования отчетов входного или выходного сигналов цифрового фильтра. Воспользуемся разложением lnz в бесконечный степенной ряд 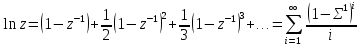 . .В результате получаем передаточную функцию в z-плоскости для цифрового дифференцирующего фильтра 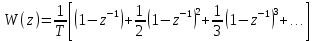 . .Передаточная функция для цифрового дифференцирующего фильтра второго порядка имеет вид 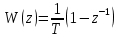 – 1 порядка – 1 порядка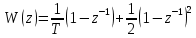 – 2 порядка – 2 порядкаРазностное уравнение представляет 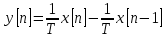 . – к 1 порядку . – к 1 порядку Структурная схема цифрового дифференцирующего фильтра первого порядка представлена на рисунке 26. 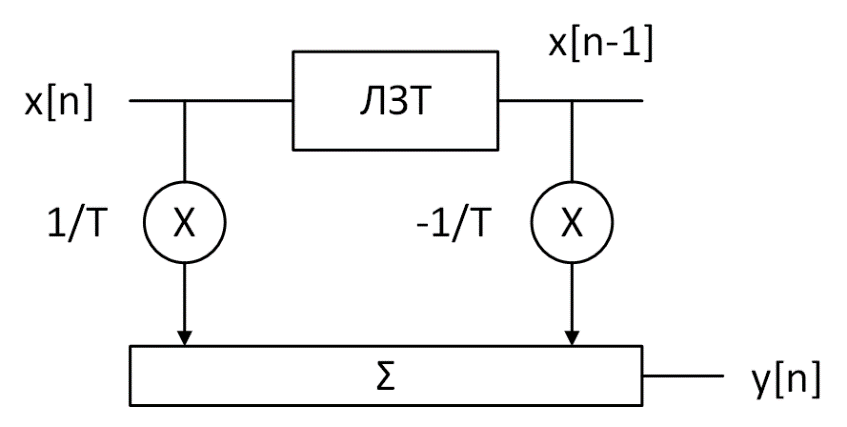 Рисунок 3 – Структурная схема цифрового дифференцирующего фильтра первого порядка После замены 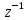 на на 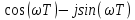 , частотная передаточная функция дифференцирующего фильтра второго порядка будет иметь вид , частотная передаточная функция дифференцирующего фильтра второго порядка будет иметь вид . .Введем новые обозначения  , ,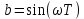 . .Для получения амплитудно-частотной характеристики (АЧХ) необходимо взять модуль по формуле  . .Таким образом получаем выражение для АЧХ дифференцирующего фильтра первого порядка 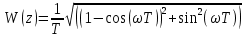 . .Из рисунка 27 видно, что на верхней частоте входного сигнала 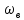 указанные АЧХ отличаются на величину указанные АЧХ отличаются на величину 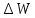 . Для определения частоты дискретизации необходимо задаться частотой . Для определения частоты дискретизации необходимо задаться частотой 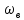 при которой нормированное отклонение АЧХ при которой нормированное отклонение АЧХ 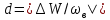 не превышало принятого значения не превышало принятого значения 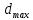 . .Поскольку частота и период – обратные величины, основываясь на условии, описанном выше, был выбран период дискретизации Т = 0,005 c (рис. 28). 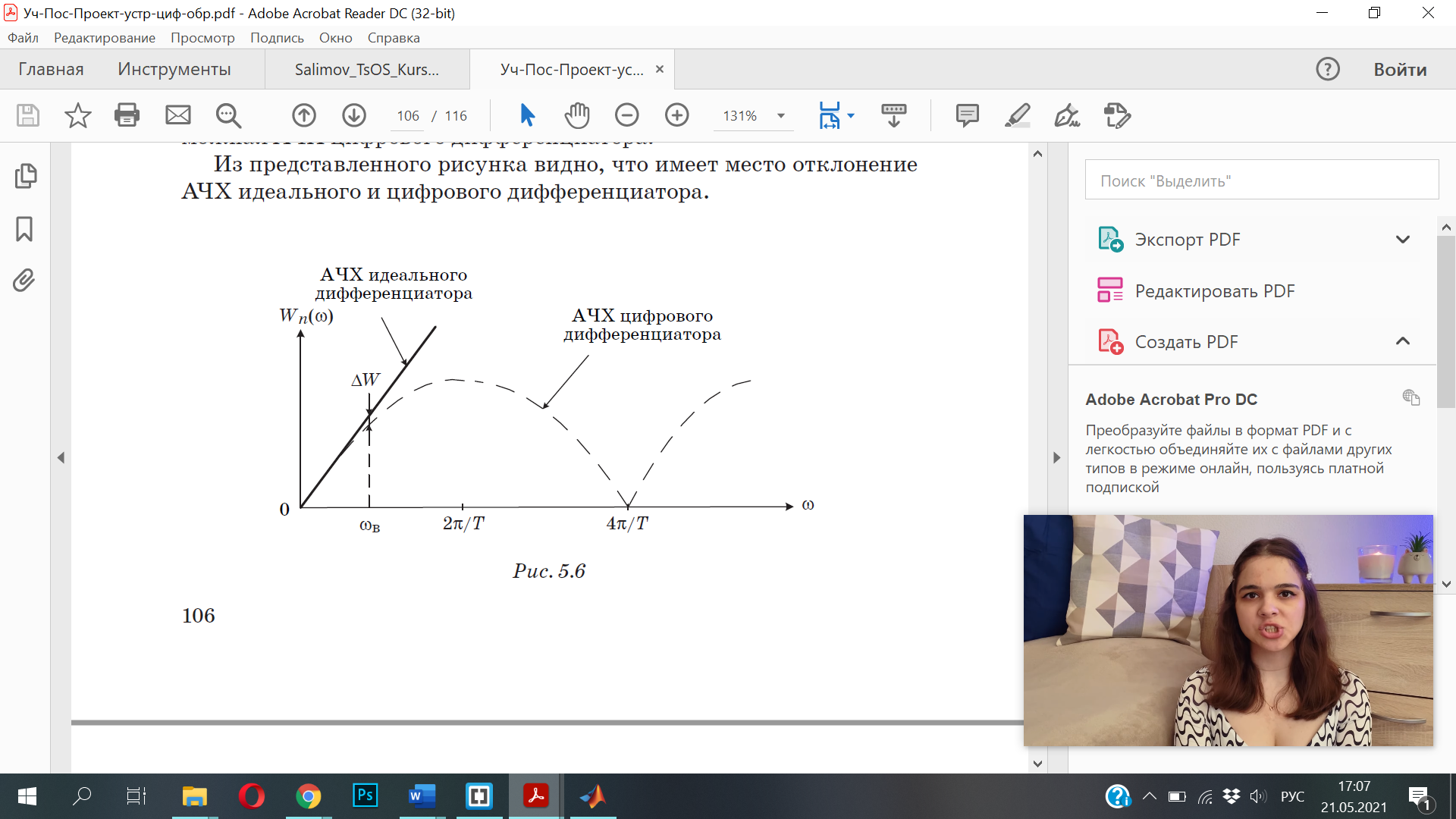 Рисунок 4 – АЧХ идеального дифференциатора и возможная АЧХ цифрового дифференциатора 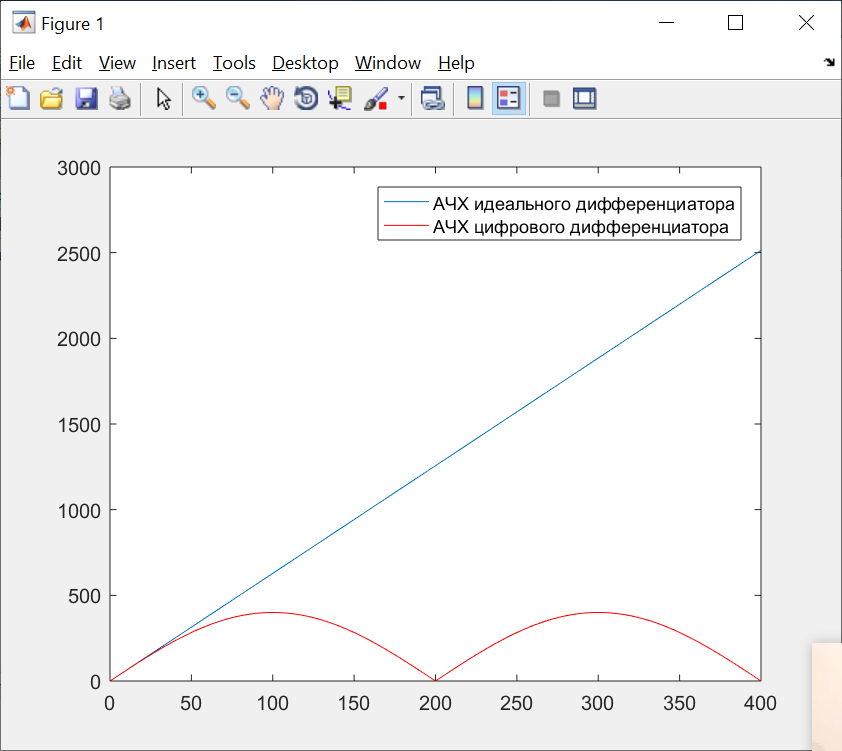 Рисунок 5 – График АЧХ дифференцирующего фильтра первого порядка ПРИЛОЖЕНИЕ А.Код MATLABT=0.005 f=0:1:400 w=2.*pi.*f a=1-cos(w.*T) b=sin(w.*T) W1=w W2=1./T.*sqrt(a.^2+b.^2) figure(1) plot(f, W1) hold on plot (f, W2, 'r') legend('АЧХ идеального дифференциатора','АЧХ цифрового дифференциатора') |
