|
Задание к курсовой работе
по дисциплине «ОБЩАЯ ТЕОРИЯ СВЯЗИ»
для студентов заочной формы обучения
по направлению подготовки 11.03.02 «Инфокоммуникационные технологии и системы связи»
Тема: «Расчет цифровой системы связи для передачи непрерывных сообщений»
Вариант задания выбирается по двум последним цифрам номера зачетной книжки студента.
Объектом расчета является цифровая система передачи непрерывных сообщений с импульсно-кодовой модуляцией (ЦСП с ИКМ) по каналу с шумом. Структурная схема системы включает в себя: источник сообщений (ИС), дискретизатор (Д), кодирующее устройство (Кодер), модулятор (Мод), линия связи (ЛС), демодулятор (Дем), декодер (Дек) и фильтр-восстановитель (ФВ).
Из таблицы вариантов необходимо выписать исходные данные для расчета согласно номеру своего варианта, соответствующему двум последними цифрами шифра (номера зачетной книжки):
интервал значений передаваемого сообщения;
полоса частот сообщения;
номер передаваемого квантованного уровня 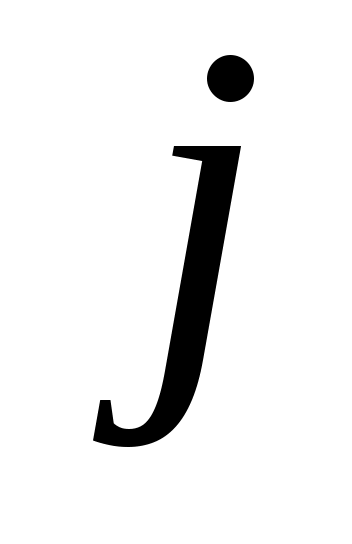 ; ;
вид модуляции (АМ, ЧМ, или ФМ);
спектральная плотность мощности шума 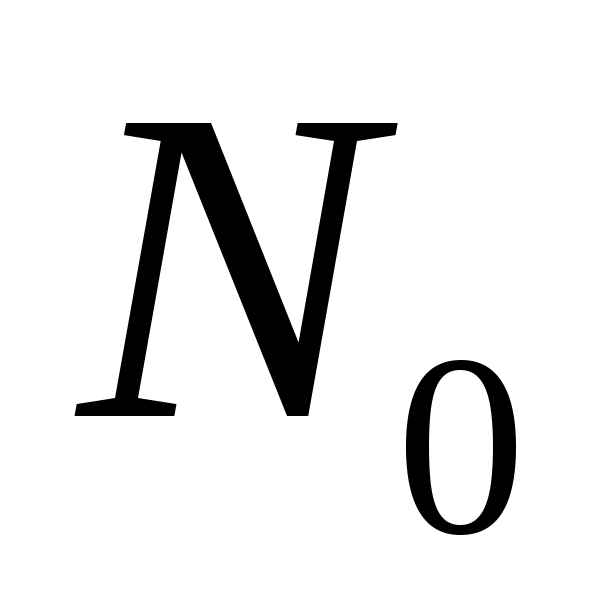 . .
Таблица вариантов.
Вариант
|
 , B , B
|
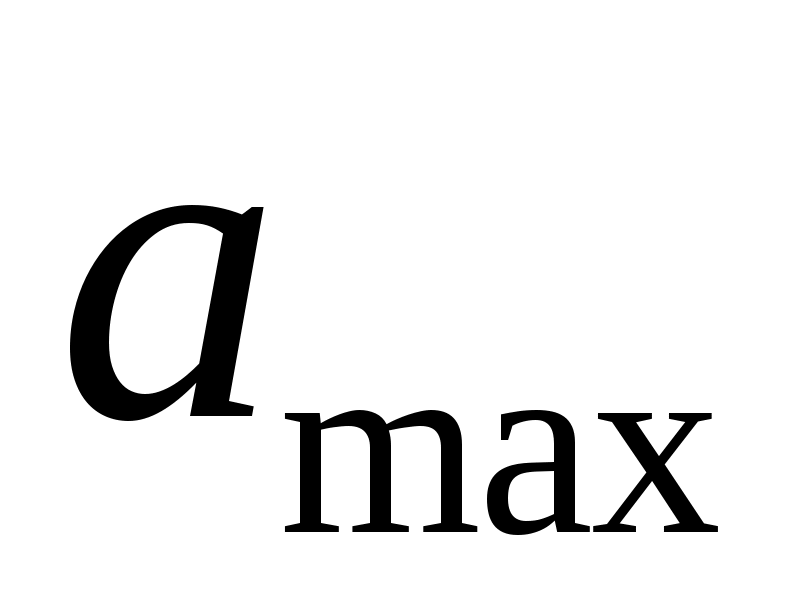 , B , B
|
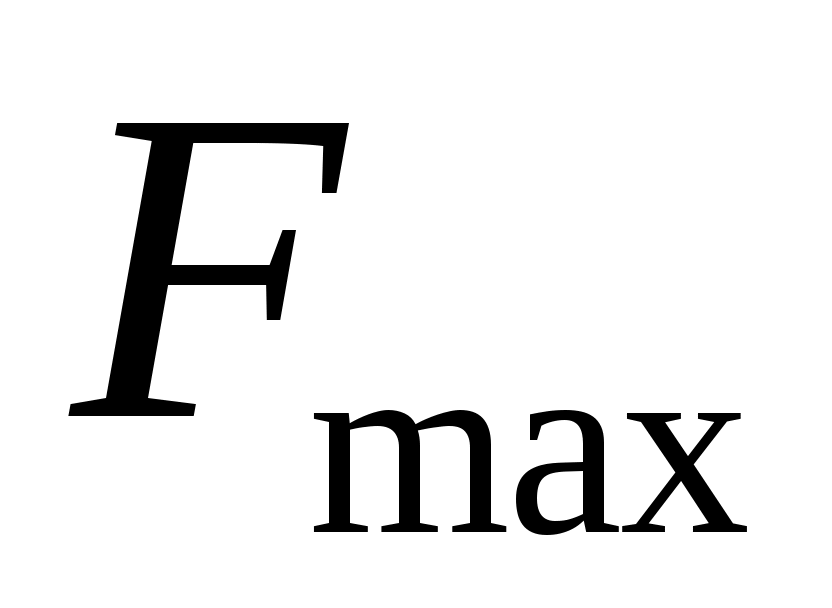 , кГц , кГц
|
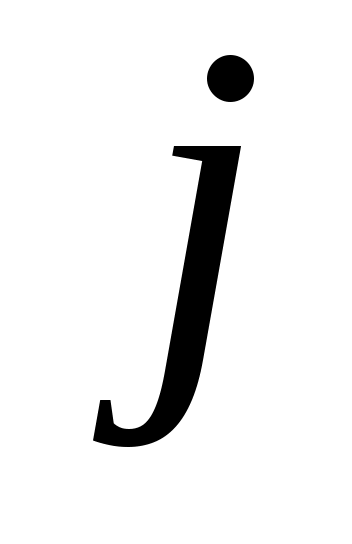
|
Вид модуляции
|
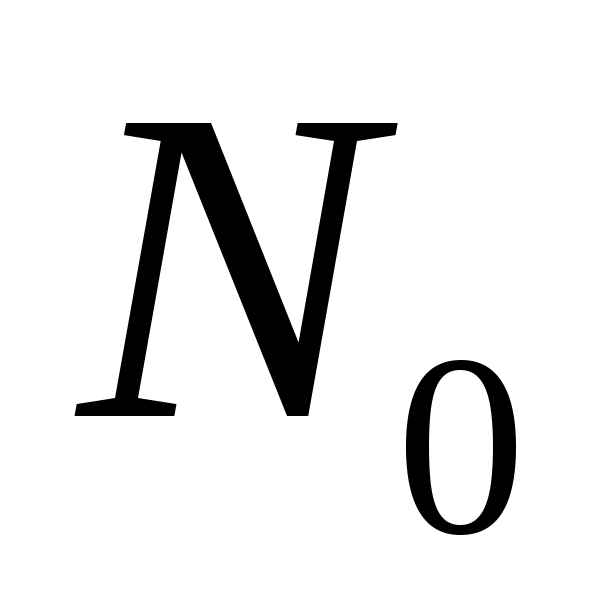 , , 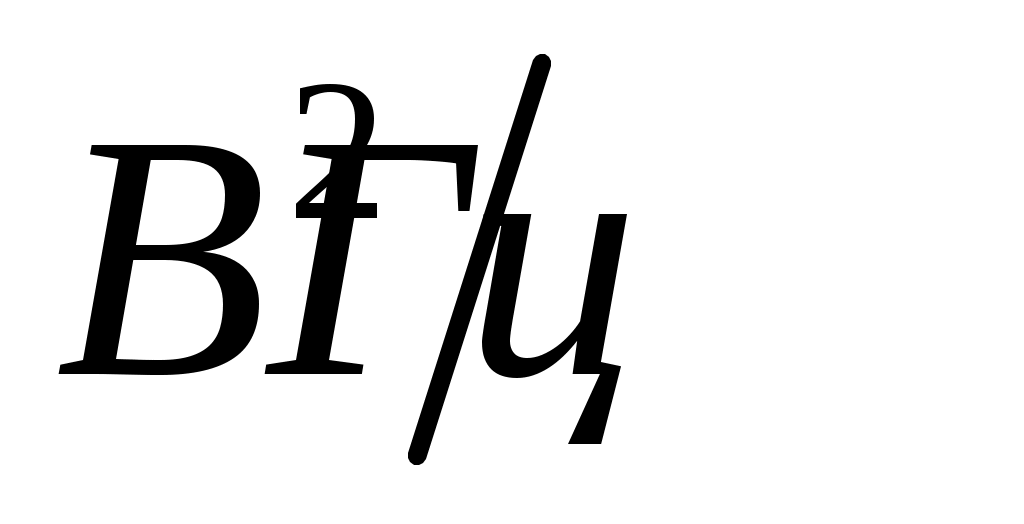
|
00/50
|
-3,2
|
+3,2
|
1
|
36/61
|
ФМ
|
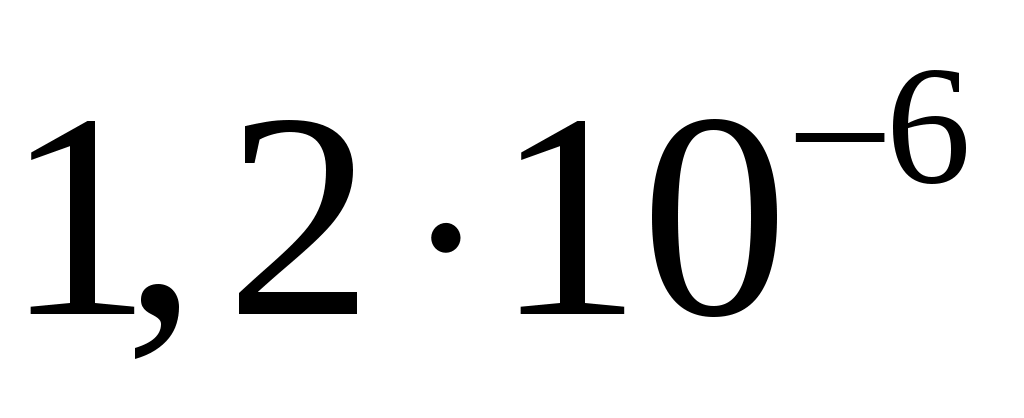
|
01/51
|
-6,4
|
+6,4
|
2
|
78/106
|
ЧМ
|
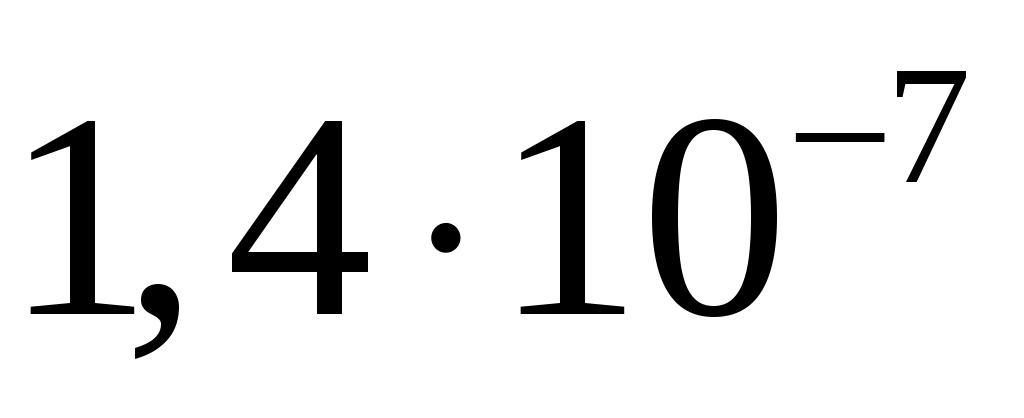
|
02/52
|
-12,8
|
+12,8
|
2,5
|
126/199
|
АМ
|
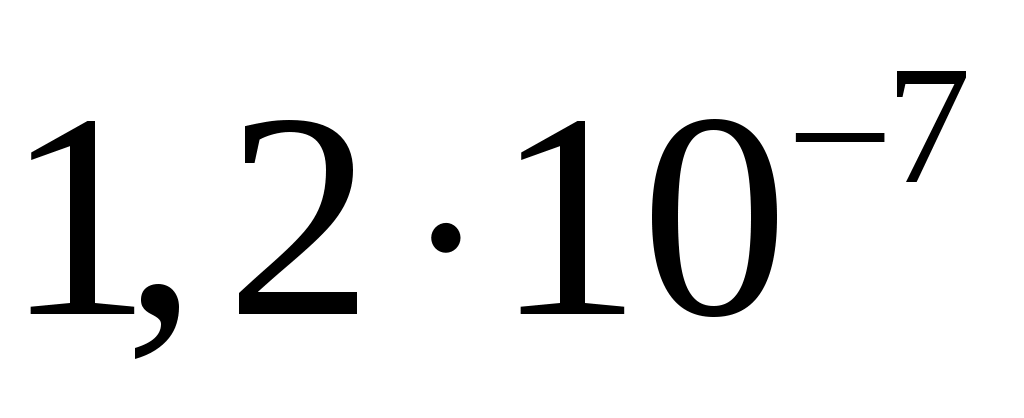
|
03/53
|
0
|
+3,2
|
3
|
29/1
|
ЧМ
|
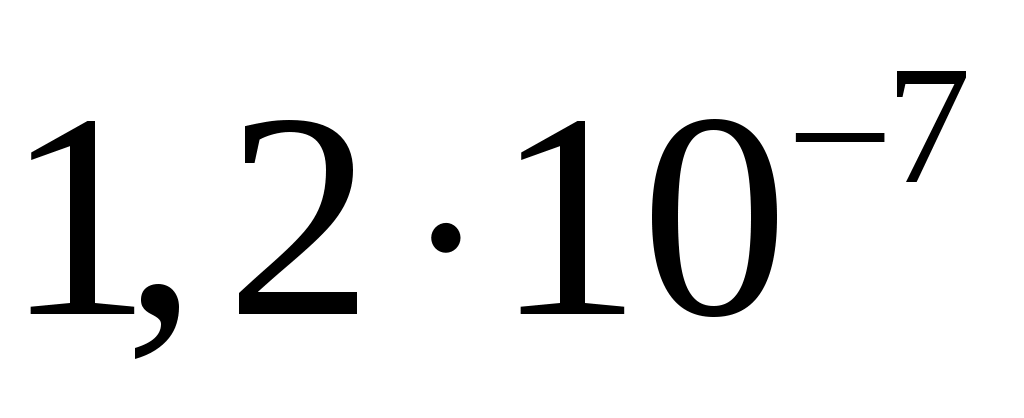
|
04/54
|
0
|
+6,4
|
3,5
|
55/62
|
ФМ
|
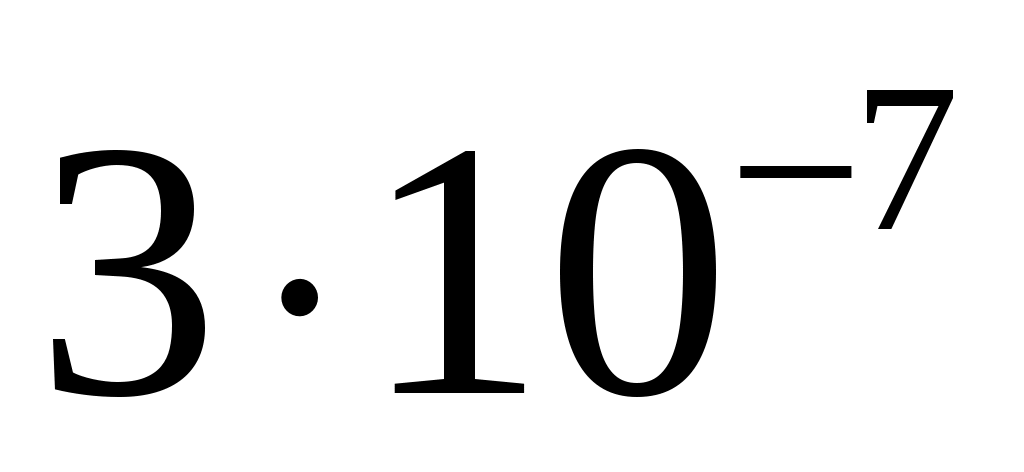
|
05/55
|
0
|
+12,8
|
1,5
|
68/75
|
АМ
|
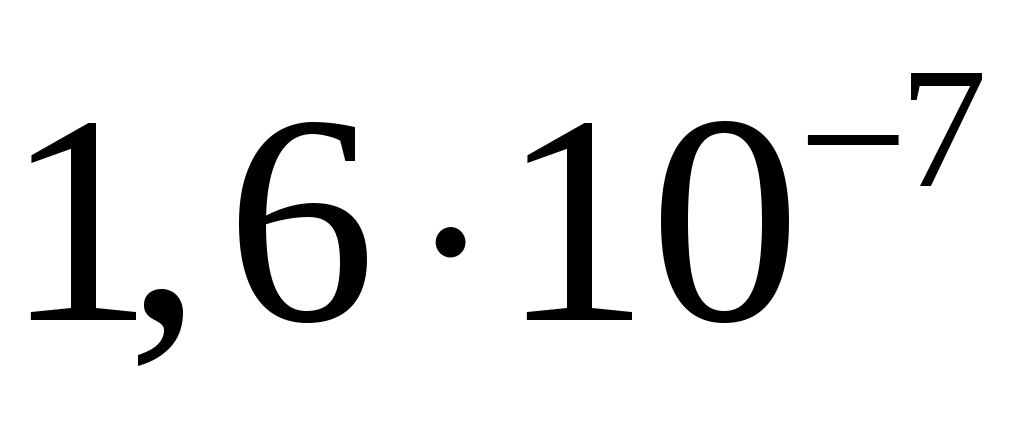
|
06/56
|
0
|
+25,6
|
2
|
131/200
|
ФМ
|
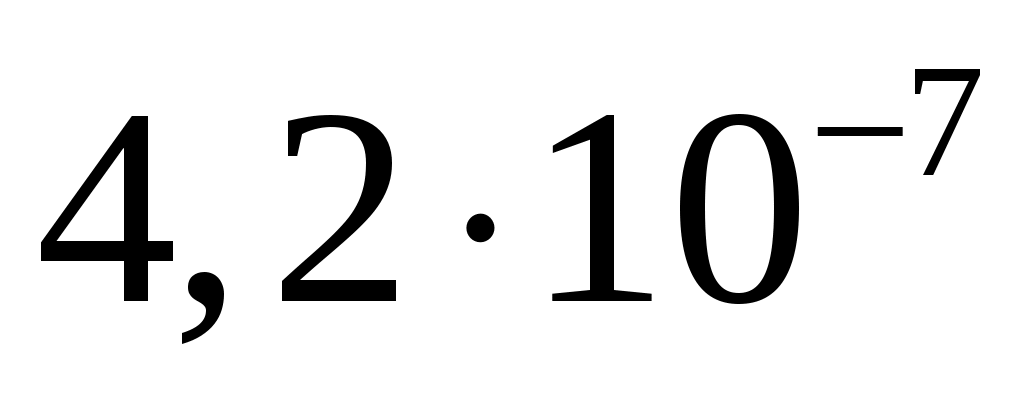
|
07/57
|
-1,6
|
+1,6
|
2,5
|
10/21
|
ЧМ
|
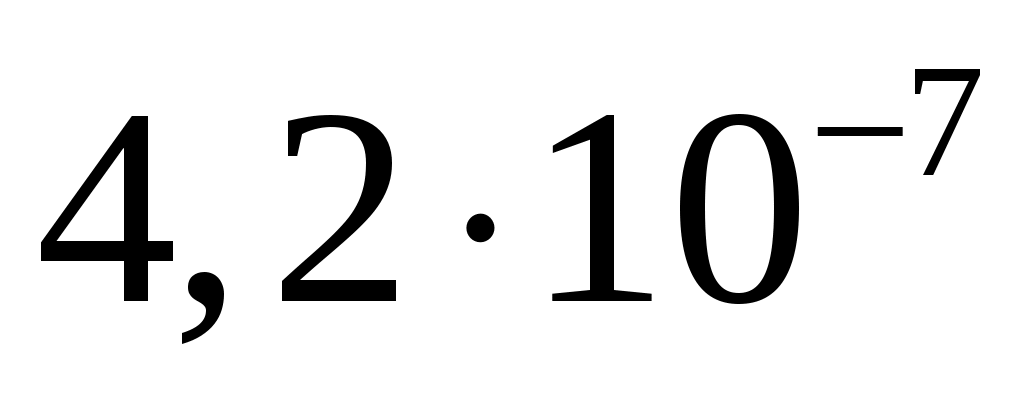
|
08/58
|
-3,2
|
+3,2
|
3
|
40/63
|
ФМ
|
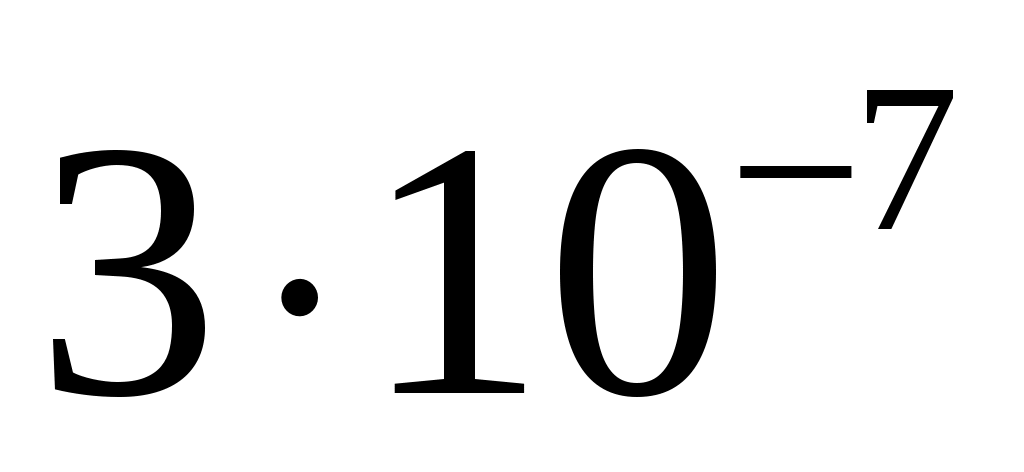
|
09/59
|
-6,4
|
+6,4
|
3,5
|
79/107
|
АМ
|
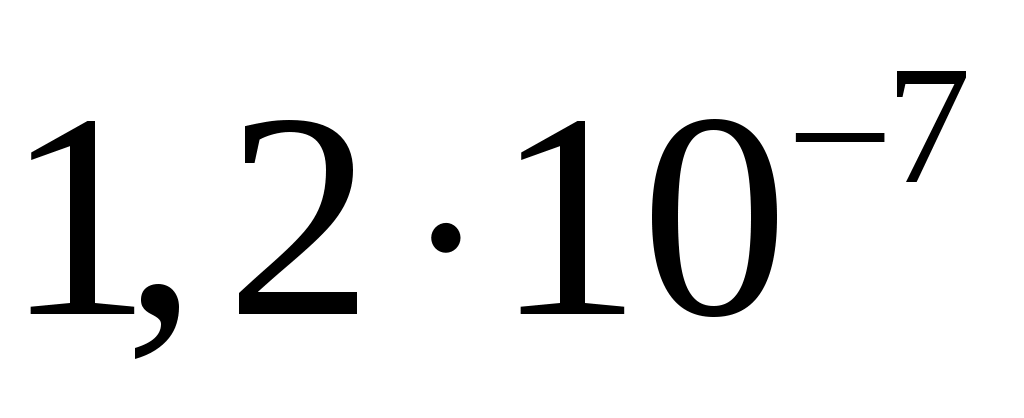
|
10/60
|
-12,8
|
+12,8
|
1
|
145/201
|
АМ
|
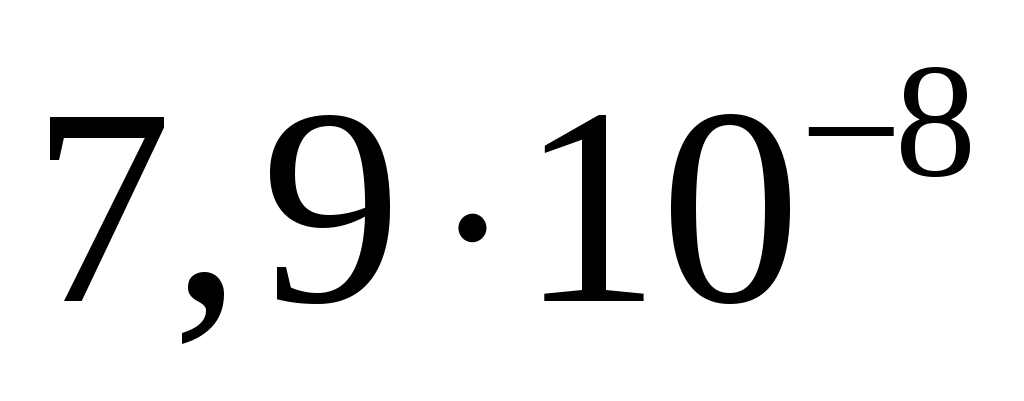
|
11/61
|
0
|
+12,8
|
1,5
|
67/72
|
ЧМ
|
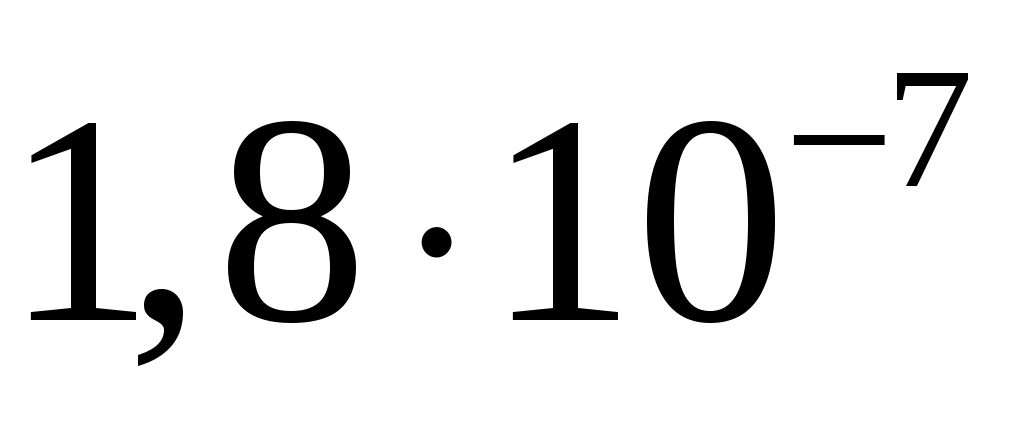
|
12/62
|
-1,6
|
+1,6
|
2
|
11/18
|
ФМ
|
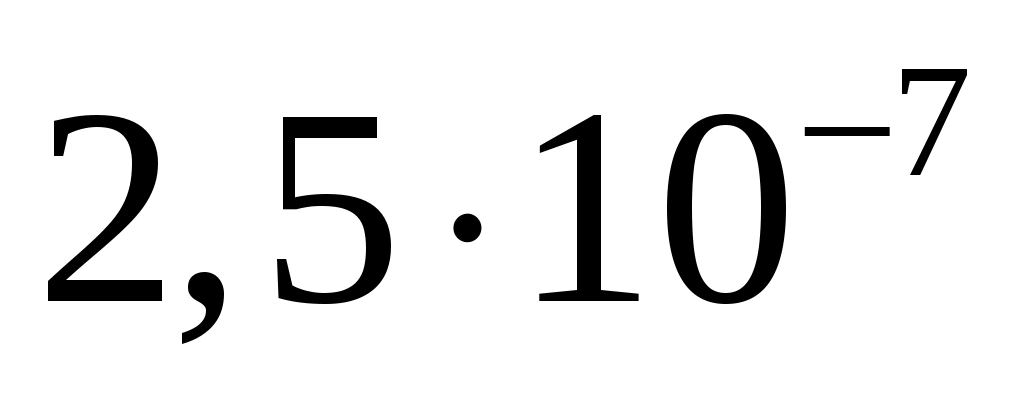
|
13/63
|
-1,6
|
+1,6
|
2,5
|
15/23
|
АМ
|
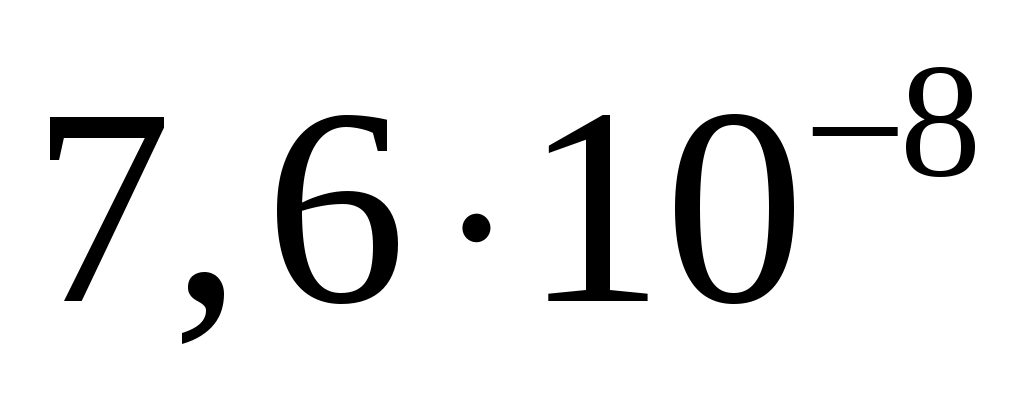
|
14/64
|
-1,6
|
+1,6
|
3
|
16/25
|
ЧМ
|
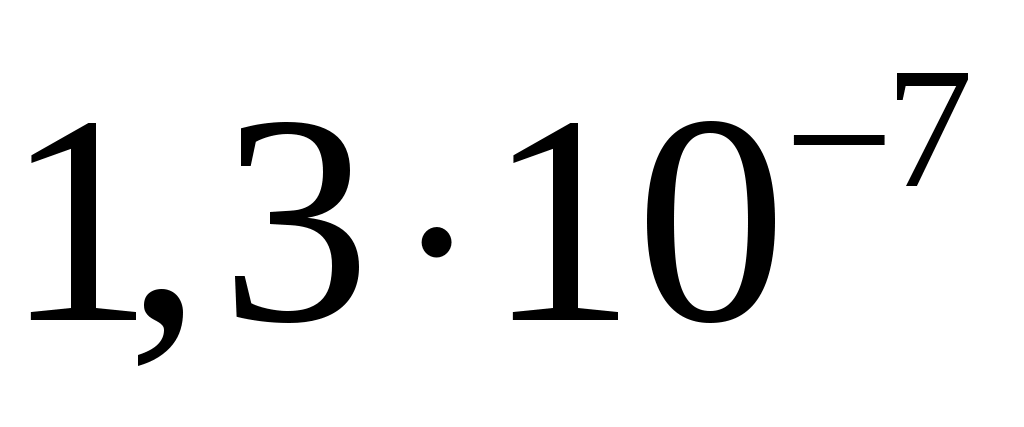
|
15/65
|
-1,6
|
+1,6
|
3,5
|
14/27
|
ФМ
|
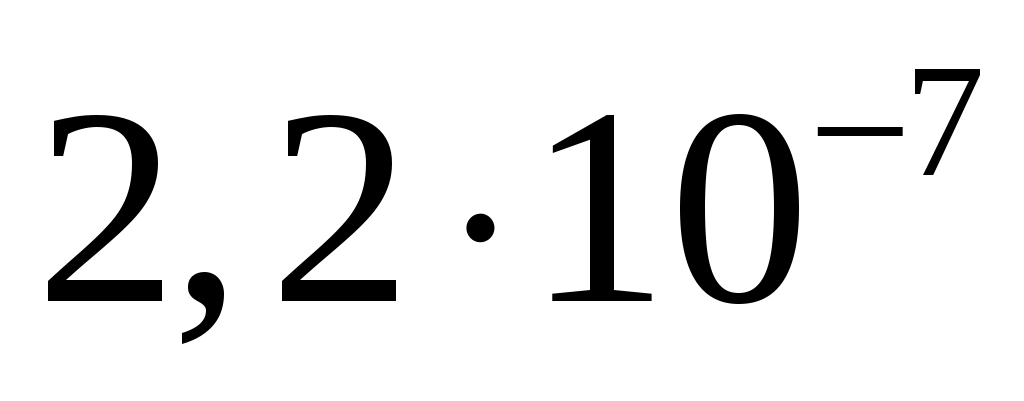
|
16/66
|
-1,6
|
+1,6
|
1
|
5/19
|
АМ
|
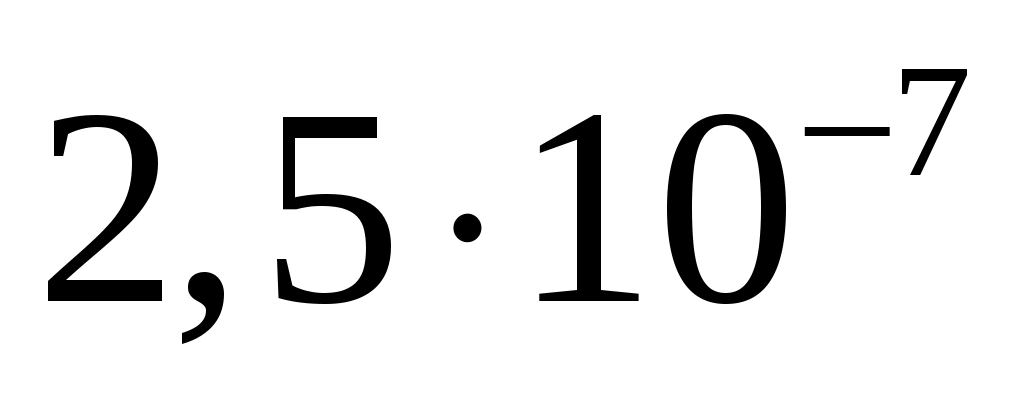
|
17/67
|
-3,2
|
+3,2
|
1,5
|
30/43
|
ЧМ
|
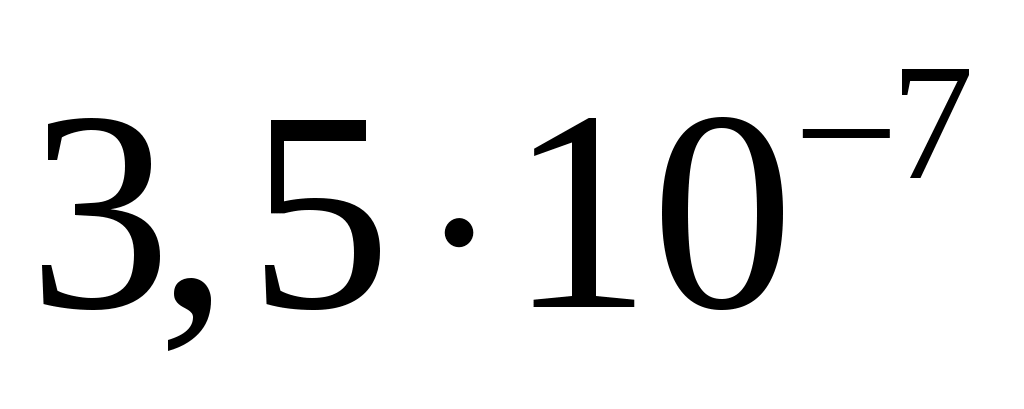
|
18/68
|
-6,4
|
+6,4
|
2
|
76/101
|
ФМ
|
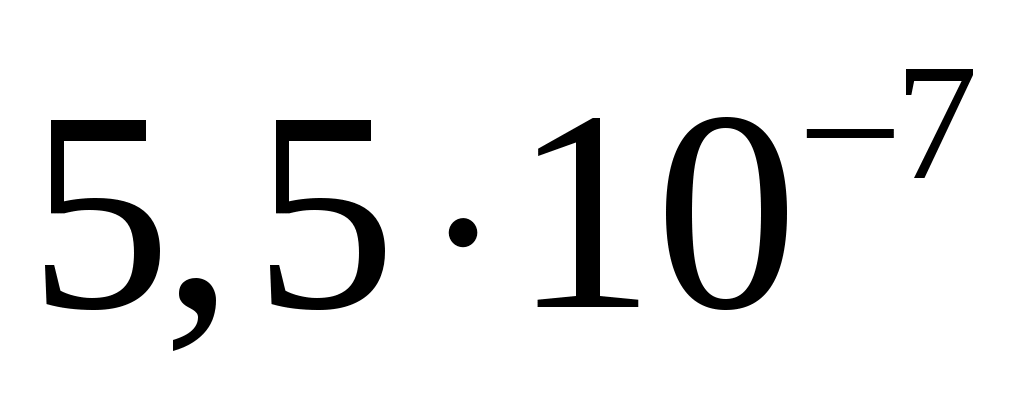
|
19/69
|
-12,8
|
+12,8
|
2,5
|
126/196
|
АМ
|
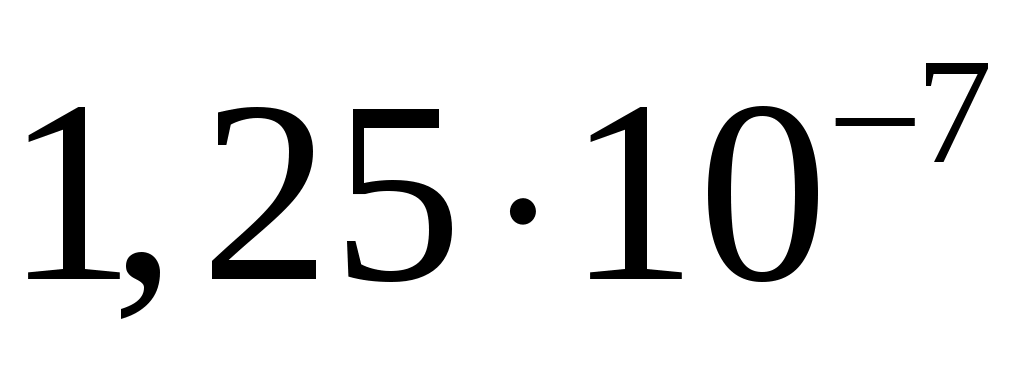
|
20/70
|
0
|
+3,2
|
3
|
28/2
|
ФМ
|
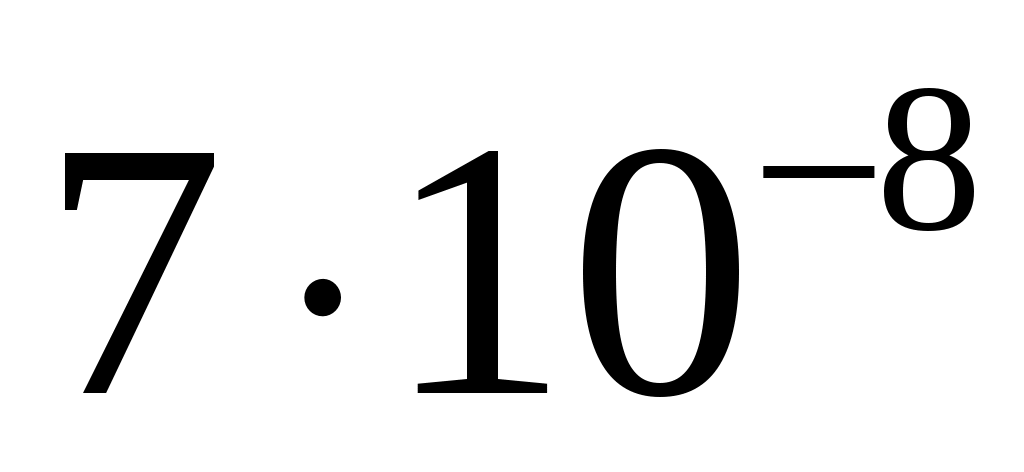
|
21/71
|
0
|
+6,4
|
3,5
|
54/59
|
ЧМ
|
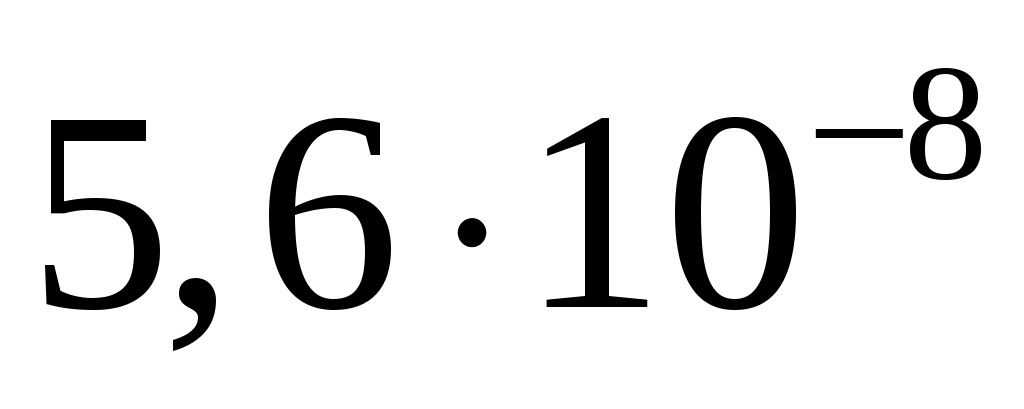
|
22/72
|
0
|
+12,8
|
1
|
69/74
|
АМ
|
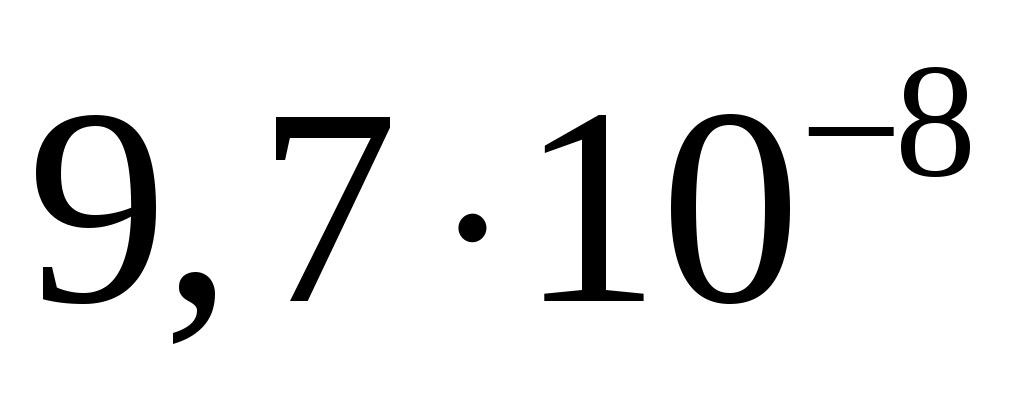
|
23/73
|
0
|
+25,6
|
1,5
|
124/197
|
ФМ
|
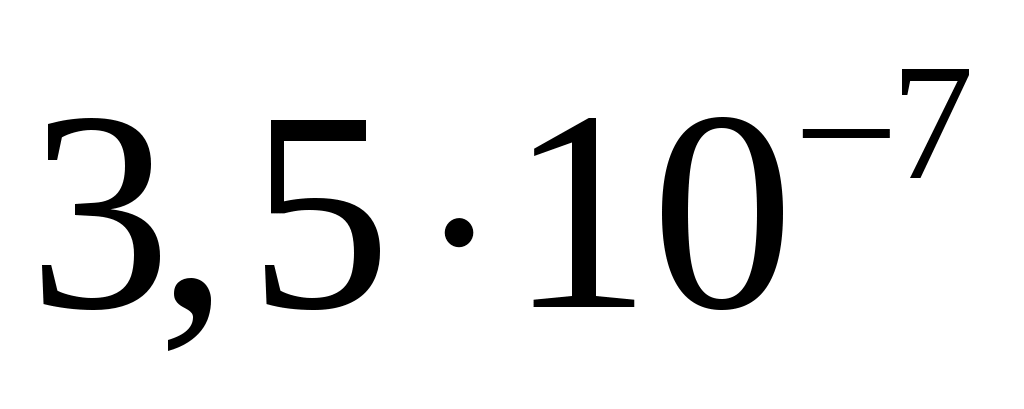
|
24/74
|
-1,6
|
+1,6
|
2
|
8/20
|
АМ
|
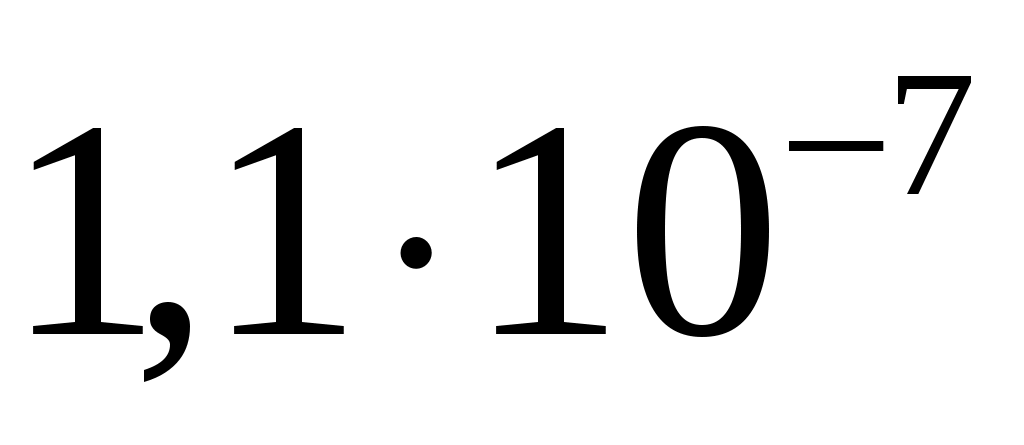
|
25/75
|
-3,2
|
+3,2
|
2,5
|
35/60
|
ЧМ
|
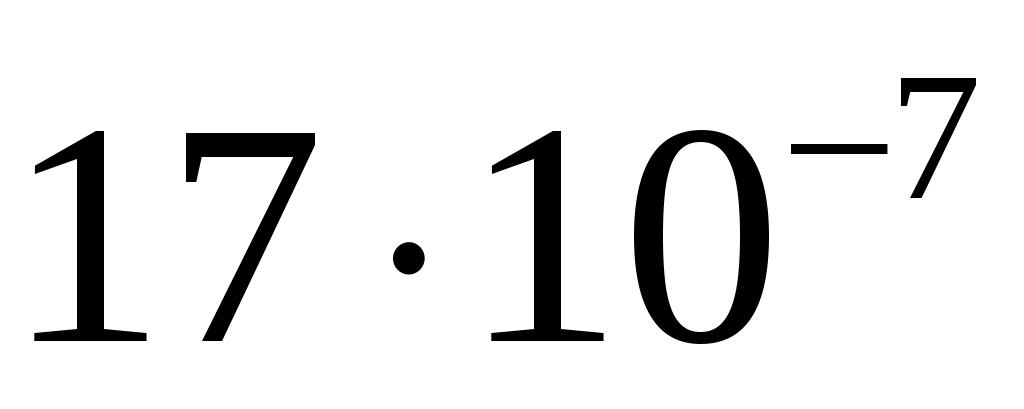
|
26/76
|
-6,4
|
+6,4
|
3
|
77/105
|
ФМ
|
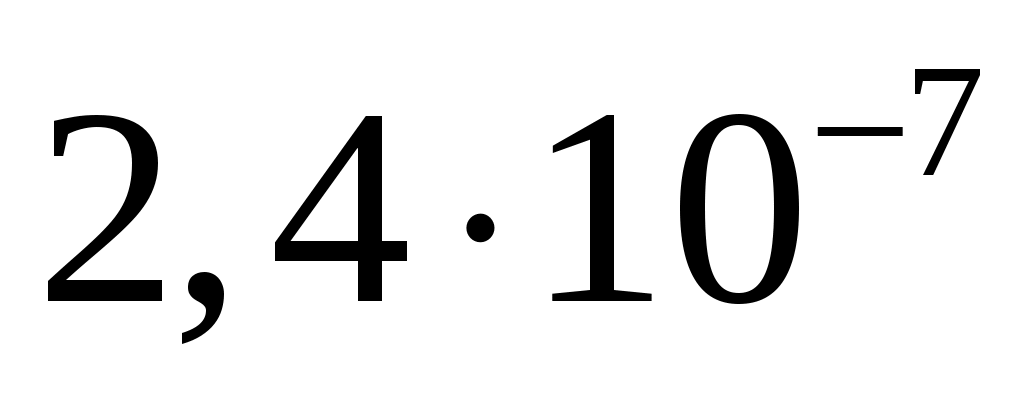
|
27/77
|
-12,8
|
+12,8
|
3,5
|
125/198
|
ФМ
|
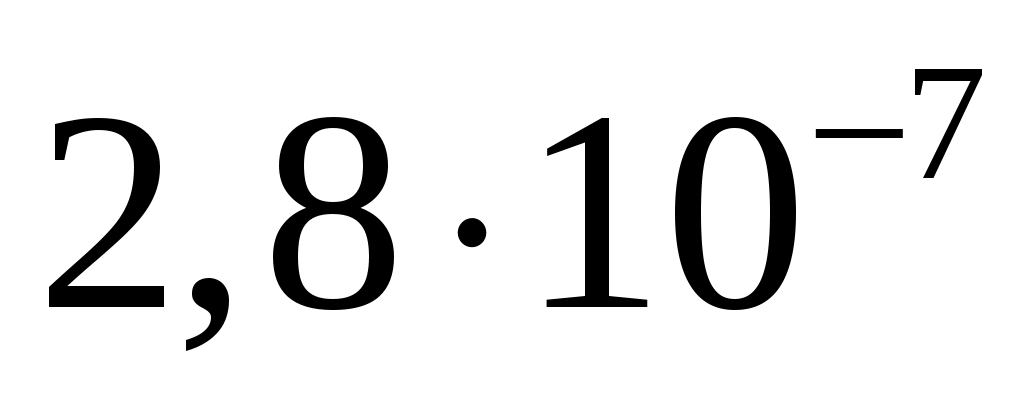
|
28/78
|
-1,6
|
+1,6
|
1
|
9/22
|
АМ
|
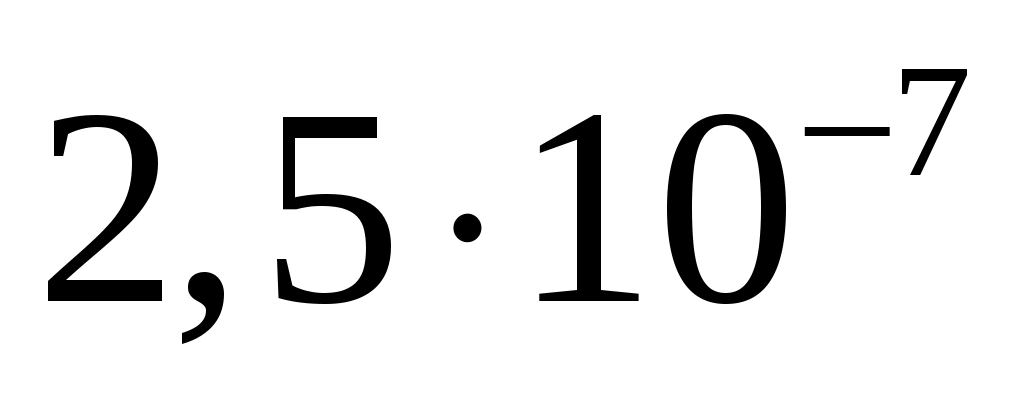
|
29/79
|
-12,8
|
+12,8
|
1,5
|
155/175
|
ЧМ
|
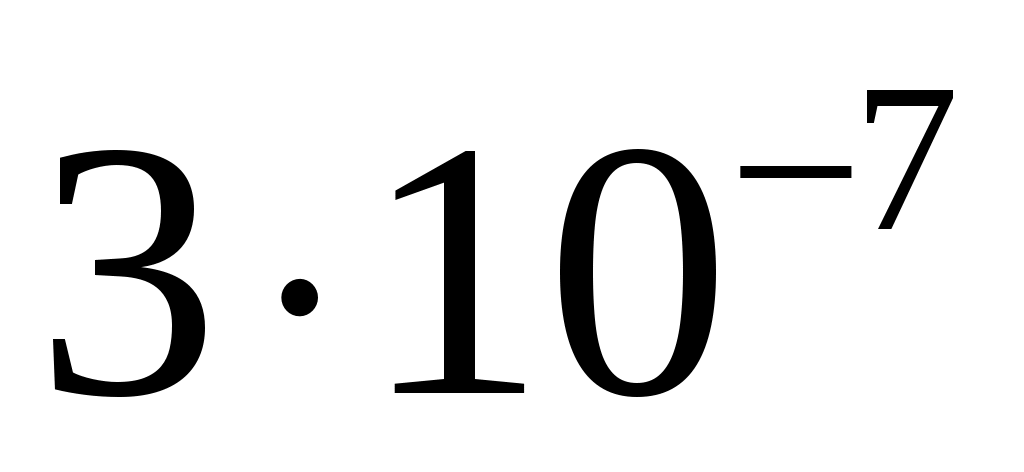
|
30/80
|
-12,8
|
+12,8
|
2
|
122/181
|
АМ
|
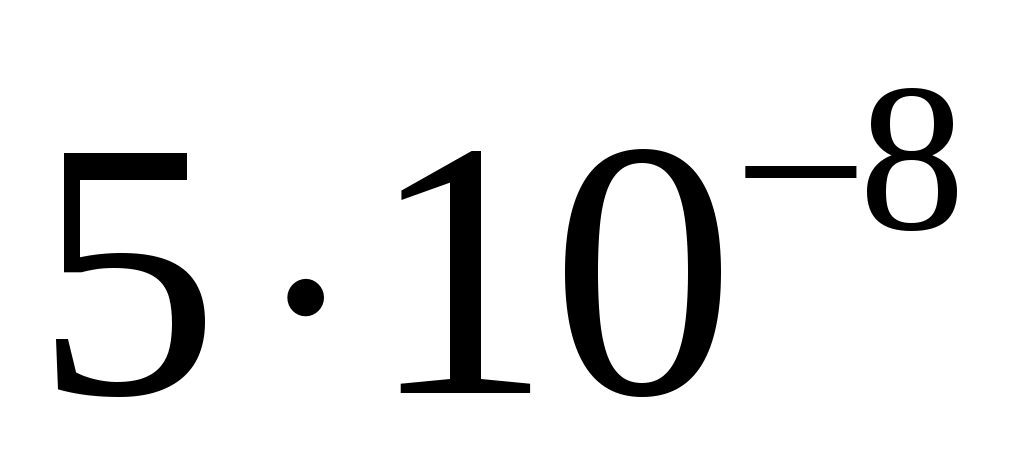
|
31/81
|
0
|
+3,2
|
2,5
|
12/26
|
ЧМ
|
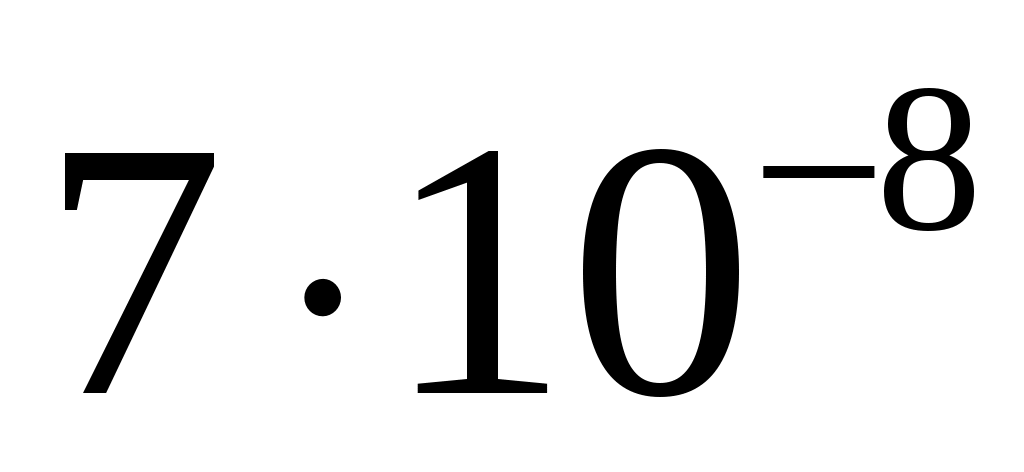
|
32/82
|
0
|
+3,2
|
3
|
3/17
|
ФМ
|
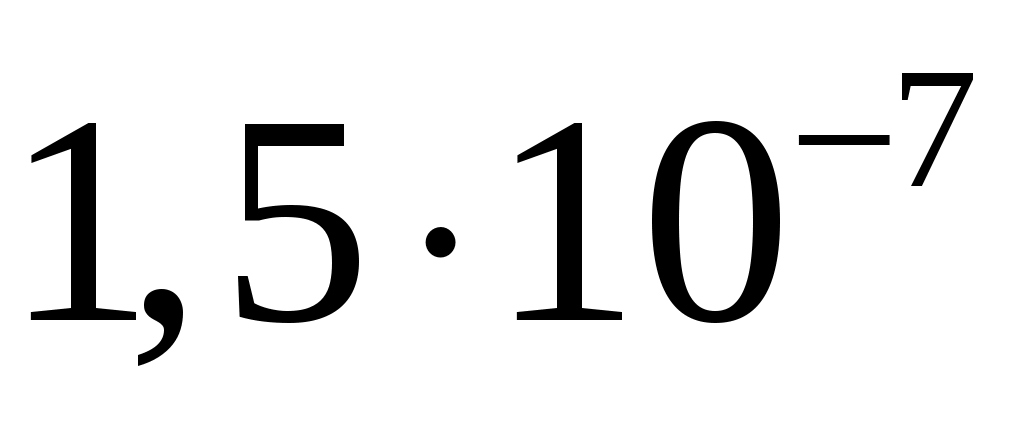
|
33/83
|
0
|
+6,4
|
3,5
|
56/46
|
ФМ
|
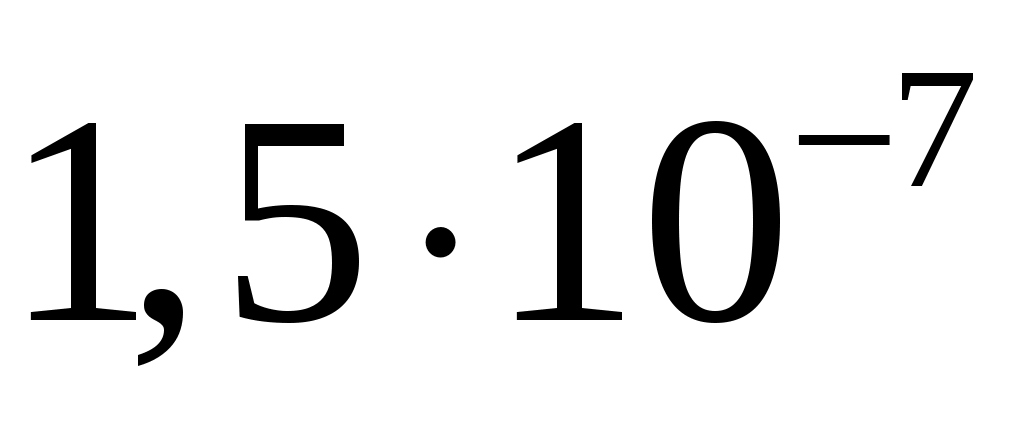
|
34/84
|
0
|
+6,4
|
1
|
57/47
|
ЧМ
|
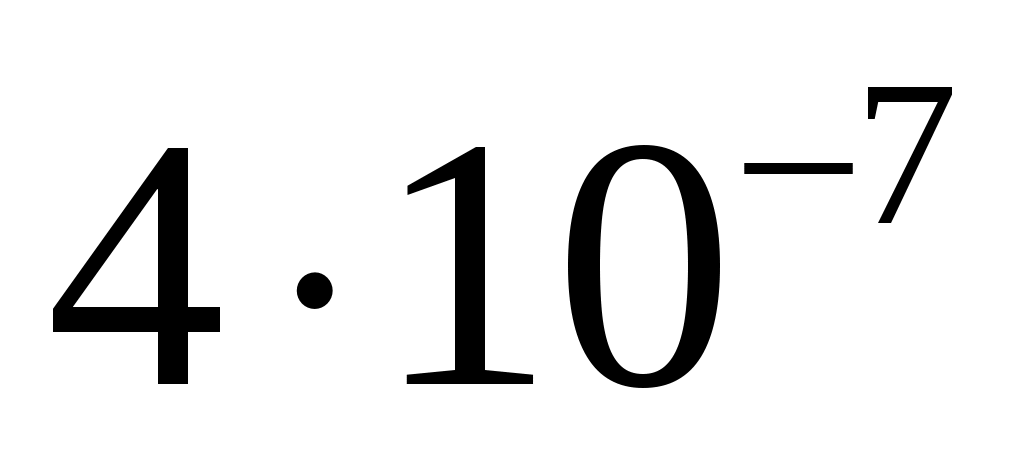
|
35/85
|
0
|
+12,8
|
1,5
|
66/71
|
АМ
|
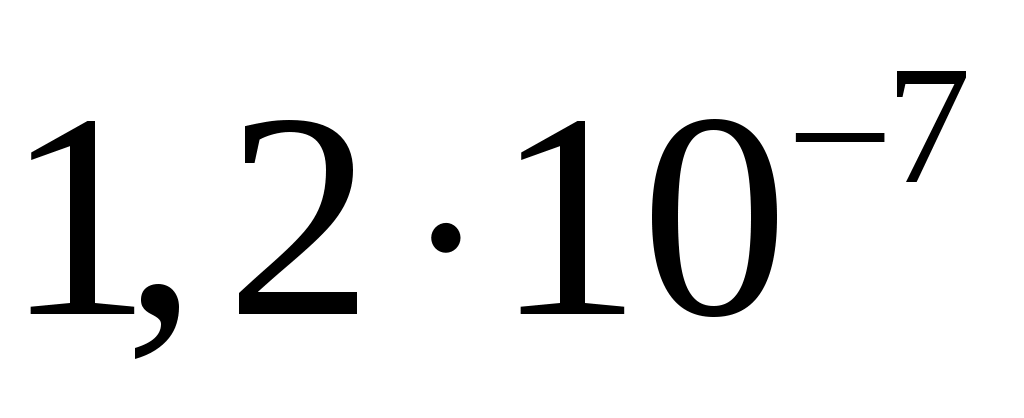
|
36/86
|
0
|
+25,6
|
2
|
65/73
|
АМ
|
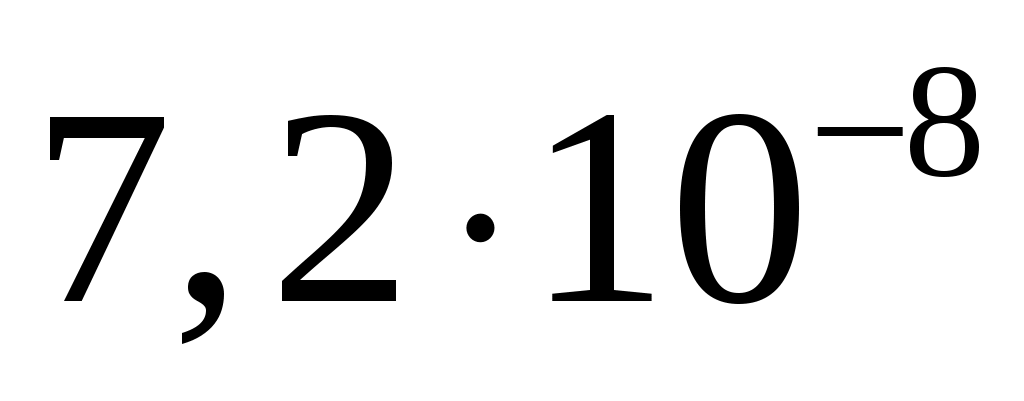
|
37/87
|
0
|
+25,6
|
2,5
|
182/19
|
ФМ
|
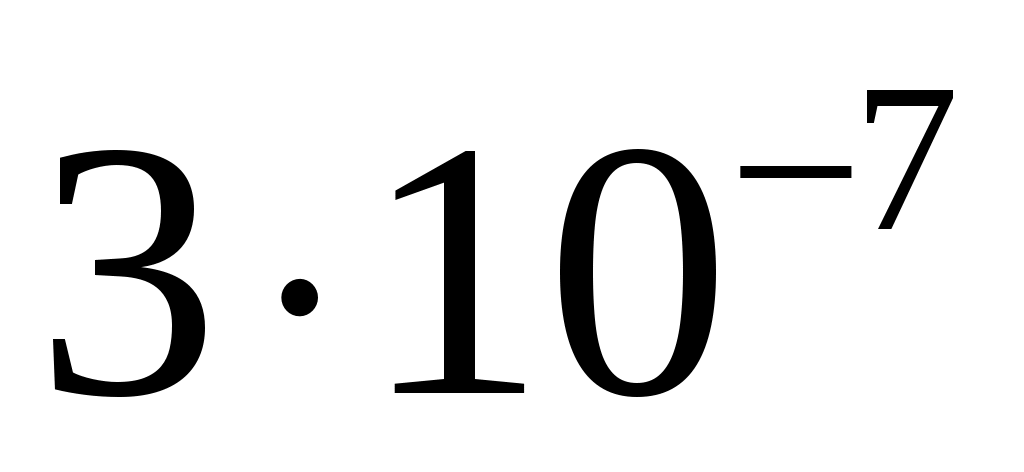
|
38/88
|
0
|
+12,8
|
3
|
121/19
|
ЧМ
|
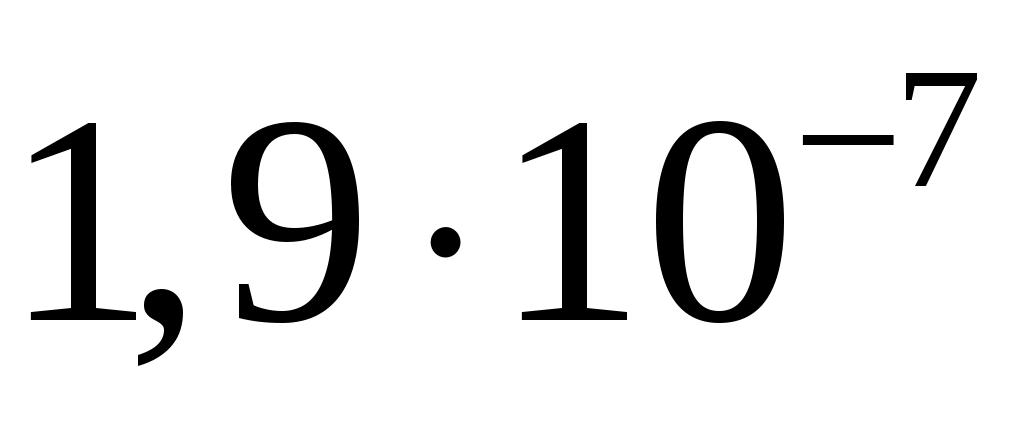
|
39/89
|
0
|
+12,8
|
3,5
|
64/71
|
АМ
|
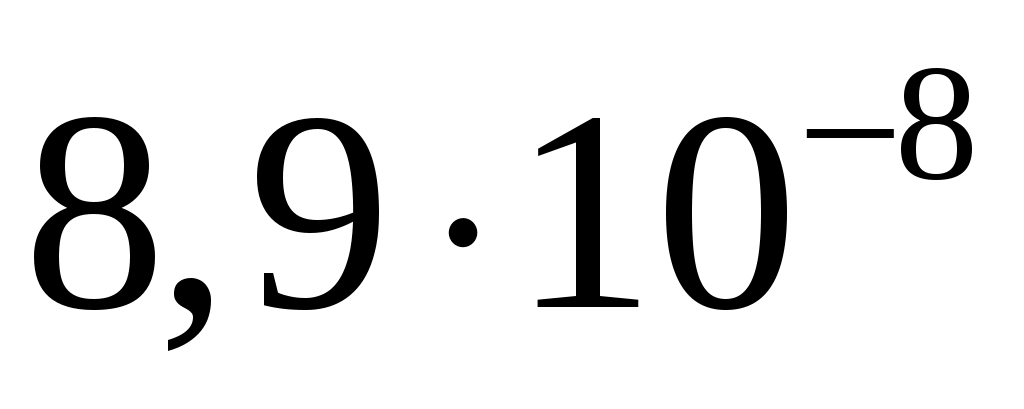
|
40/90
|
-3,2
|
+3,2
|
1
|
13/24
|
ФМ
|
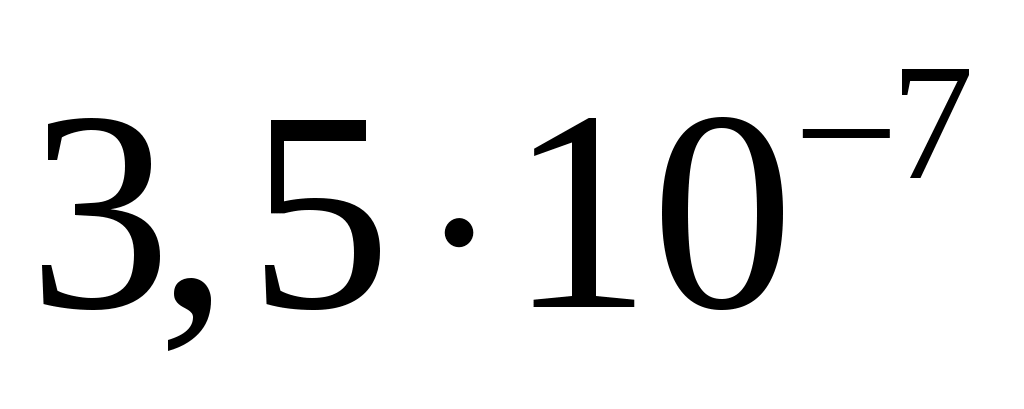
|
41/91
|
-3,2
|
+3,2
|
1,5
|
41/49
|
АМ
|
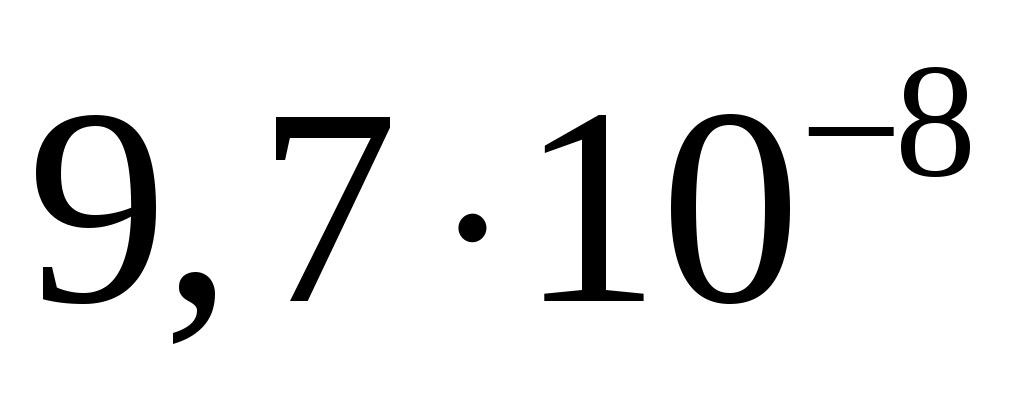
|
42/92
|
-3,2
|
+3,2
|
2
|
50/45
|
ФМ
|
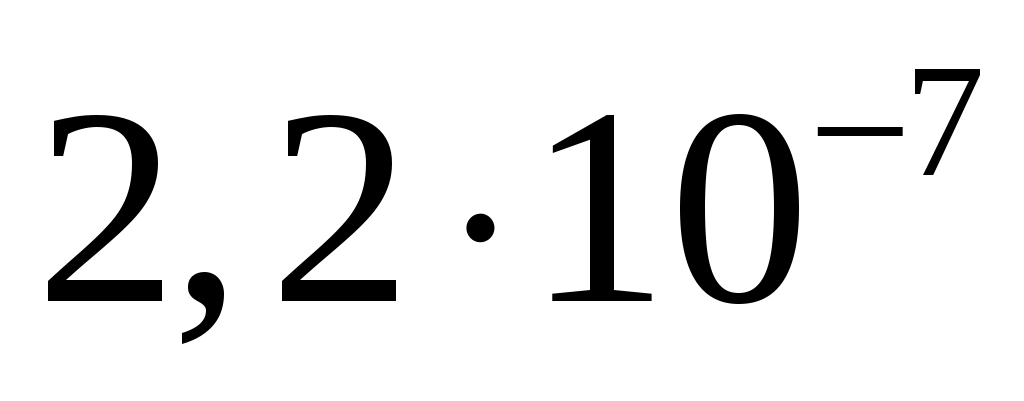
|
43/93
|
-3,2
|
+3,2
|
2,5
|
53/42
|
ЧМ
|
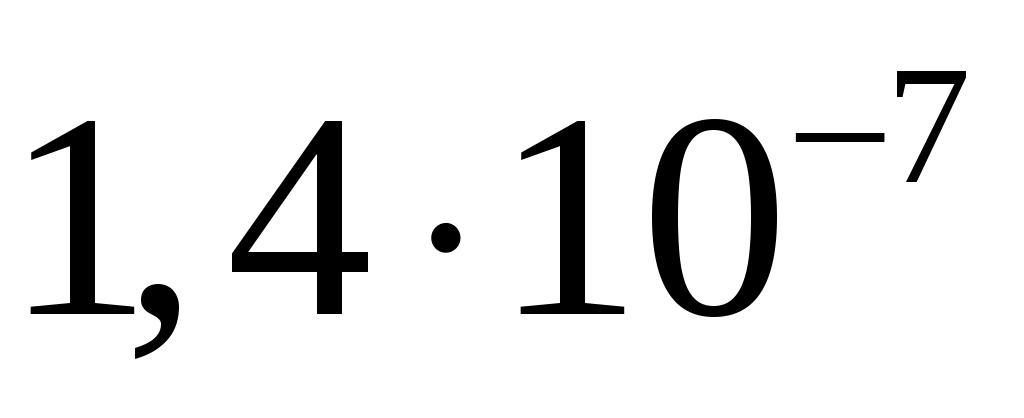
|
44/94
|
-6,4
|
+6,4
|
3
|
80/83
|
ФМ
|
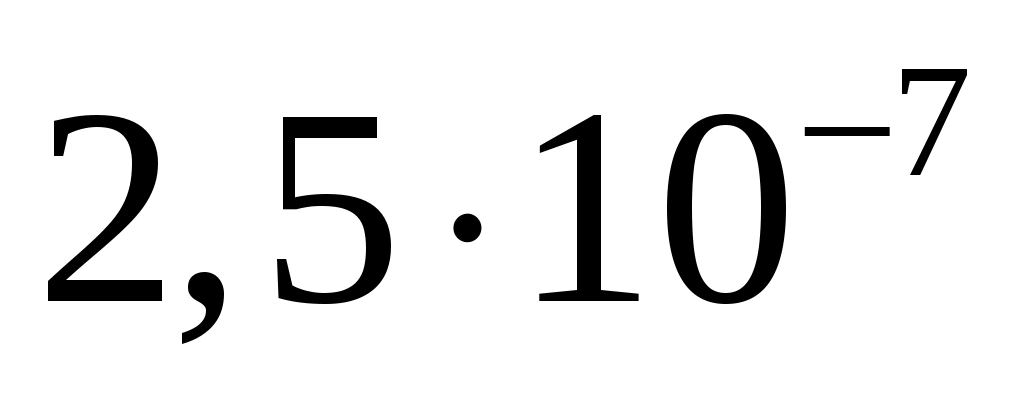
|
45/94
|
-6,4
|
+6,4
|
3,5
|
84/95
|
ЧМ
|
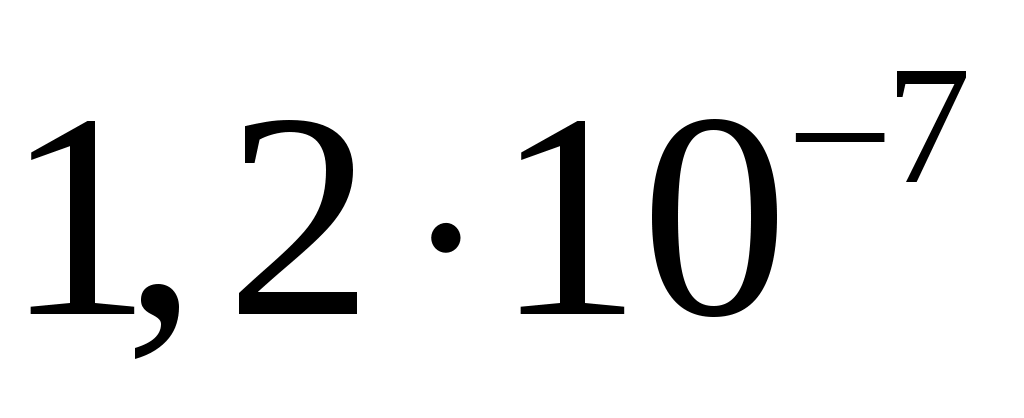
|
46/96
|
-6,4
|
+6,4
|
1
|
100/99
|
ФМ
|
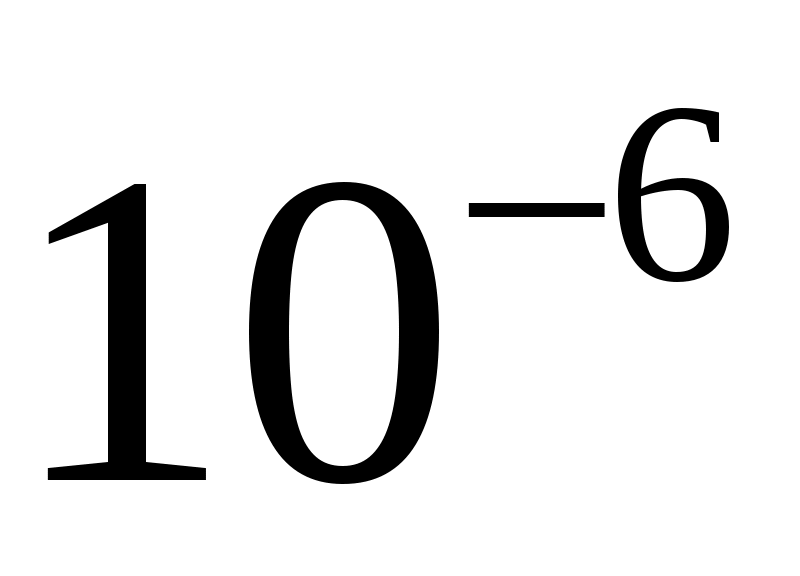
|
47/97
|
-6,4
|
+6,4
|
1
|
81/82
|
АМ
|
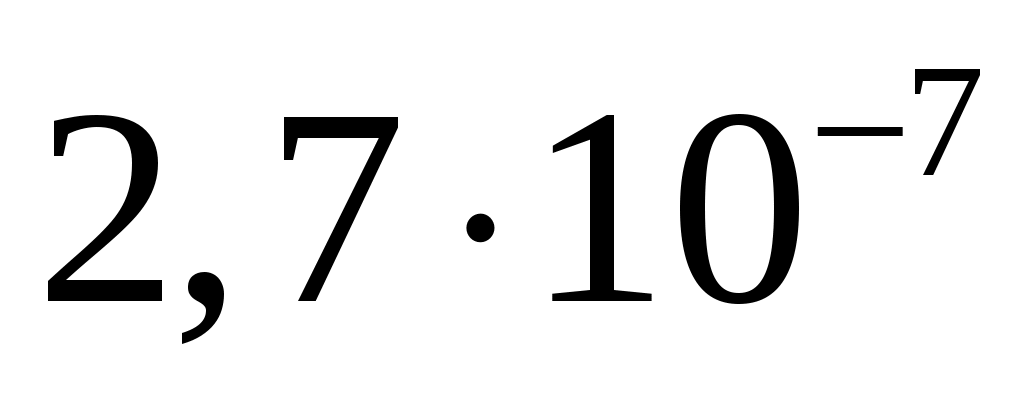
|
48/98
|
-12,8
|
+12,8
|
1,5
|
146/159
|
ЧМ
|
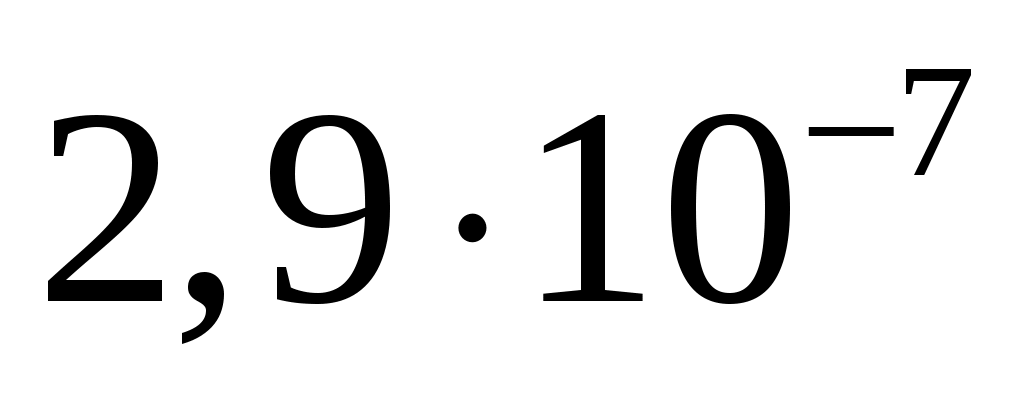
|
49/99
|
-12,8
|
+12,8
|
2
|
150/170
|
АМ
|
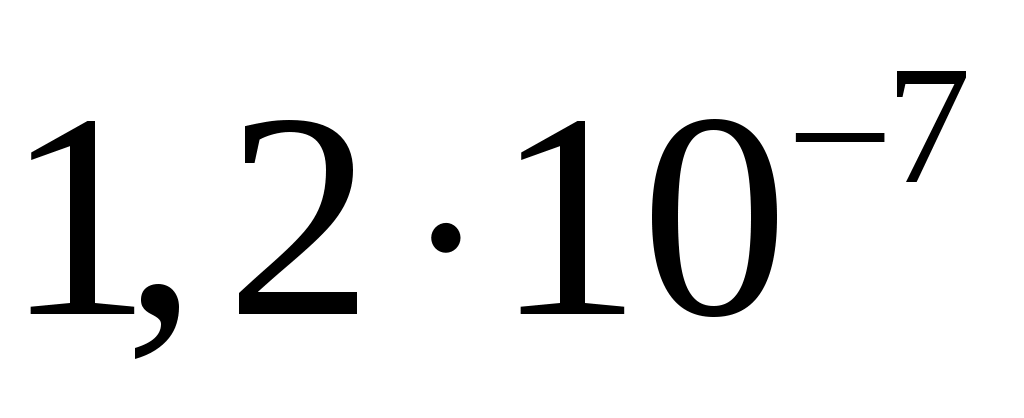
|
В курсовой работе необходимо выполнить следующие задания:
Составьте структурную схему цифровой системы передачи аналоговых сообщений. Дайте кратное описание принципа действия цифровой системы передачи аналоговых сообщений.
Определить аналитически одномерную плотность вероятности мгновенных значений сообщения 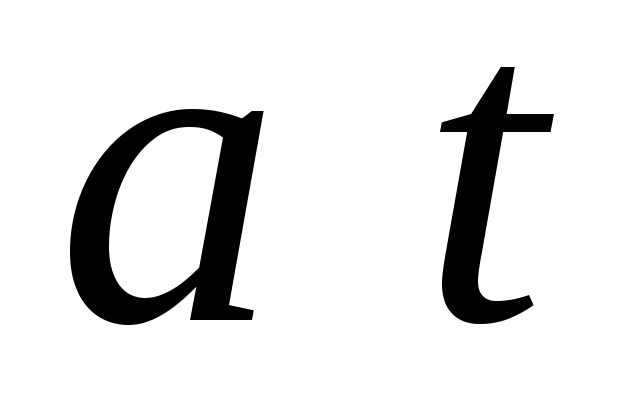 и вычислить ее значение. Произвести расчет значений математического ожидания и вычислить ее значение. Произвести расчет значений математического ожидания 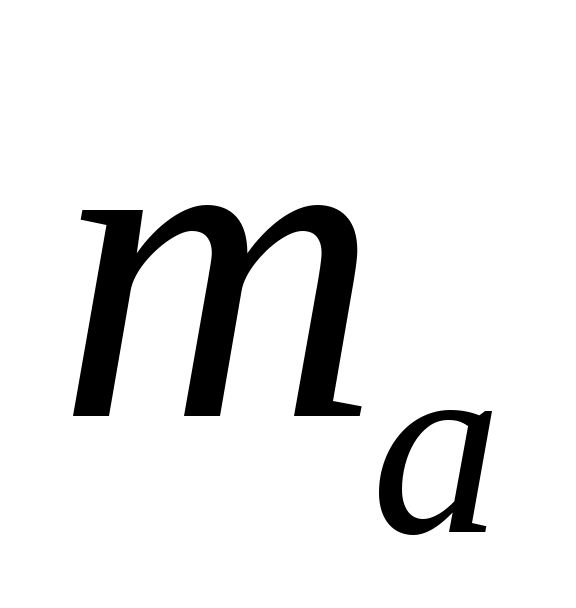 и дисперсии и дисперсии 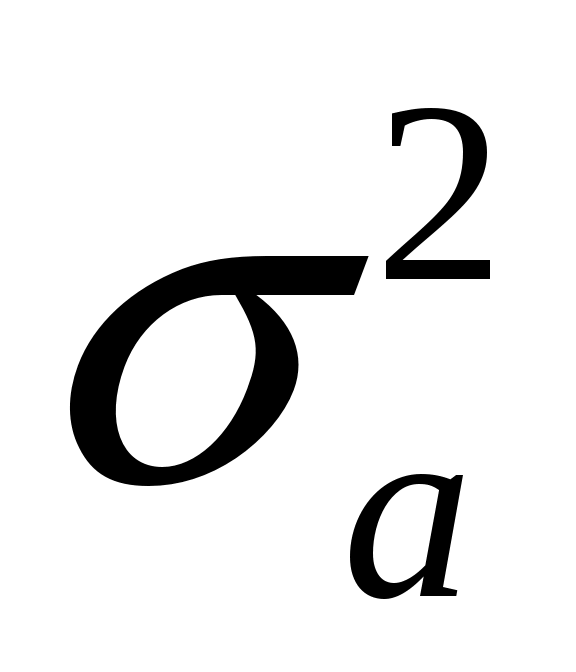 сообщения сообщения 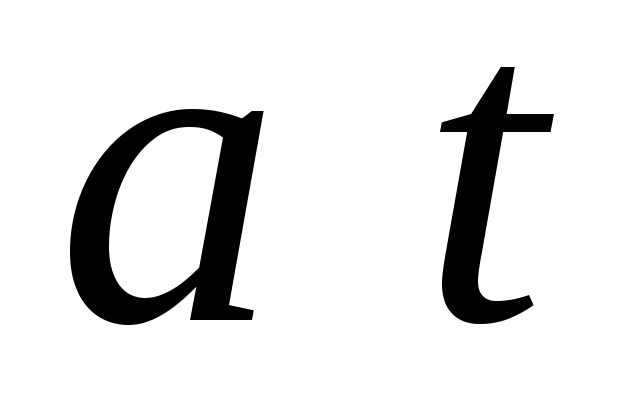 . .
Рассчитайте максимально допустимый интервал дискретизации 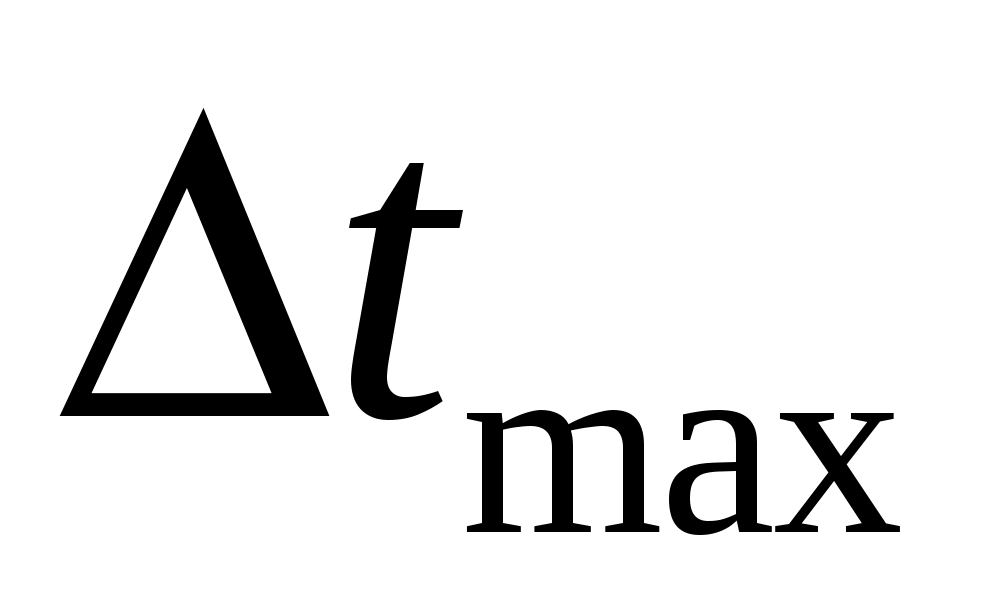 . Вычислить число уровней квантования . Вычислить число уровней квантования 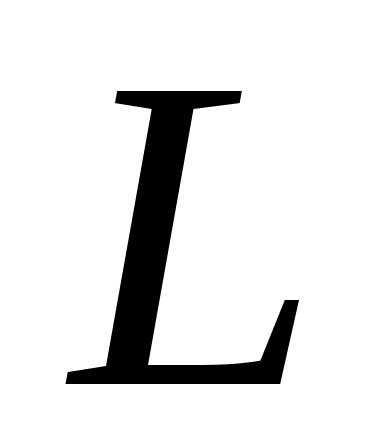 . Определить среднюю мощность шума квантования . Определить среднюю мощность шума квантования 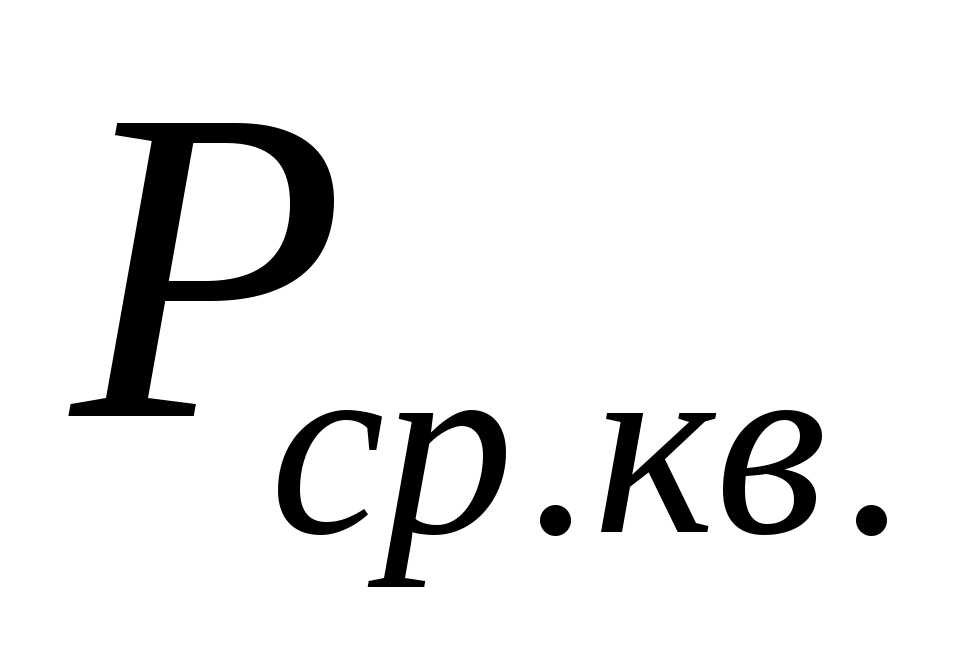 .Вычислите отношение средних мощностей сообщения .Вычислите отношение средних мощностей сообщения 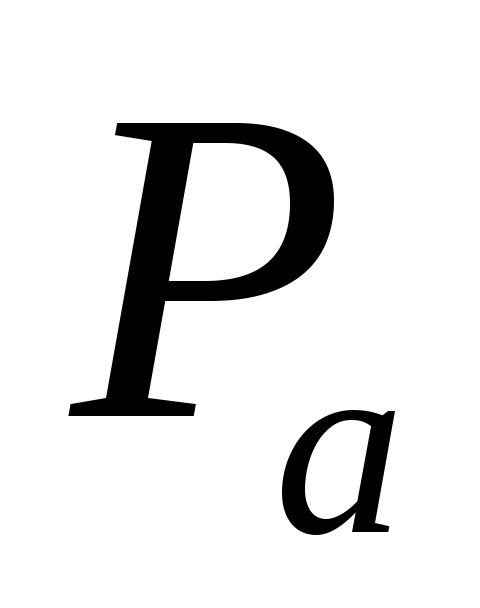 и шума квантования и шума квантования 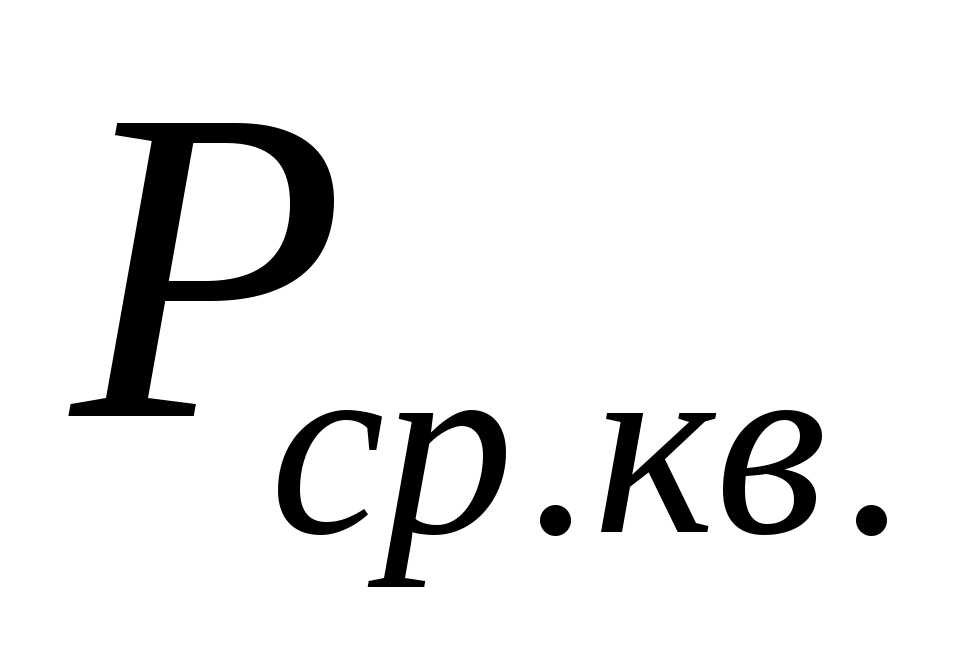 . Определить энтропию . Определить энтропию 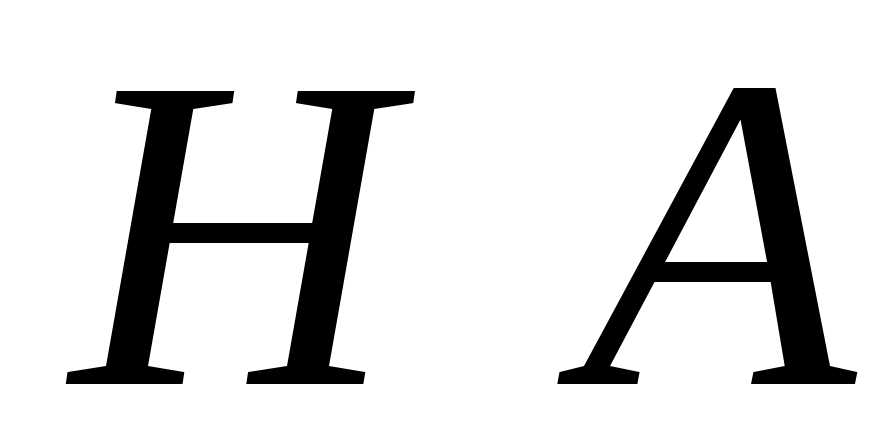 и производительность и производительность 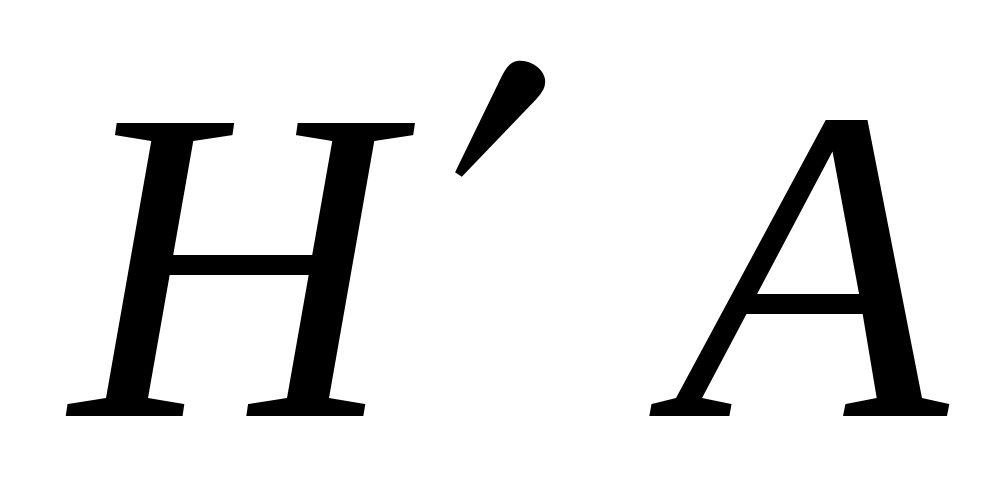 , представив дискретизатор в качестве источника дискретных сообщений с объемом алфавита , представив дискретизатор в качестве источника дискретных сообщений с объемом алфавита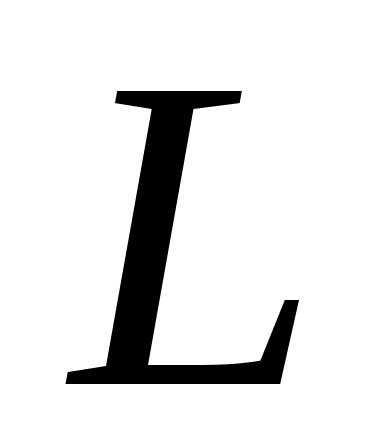 . .
Определите число разрядов примитивного кода 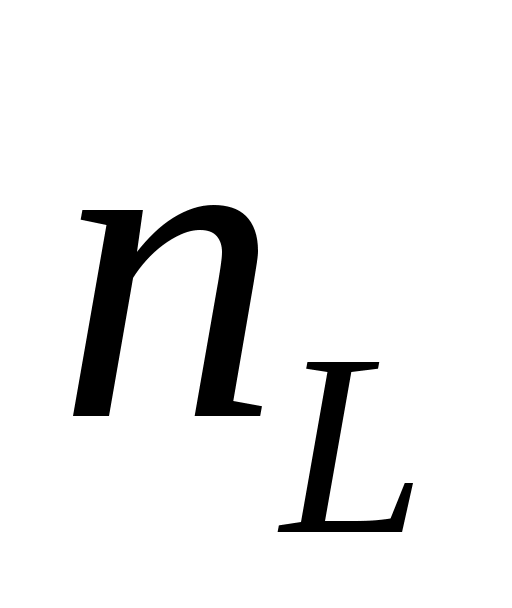 , необходимое для кодирования всех , необходимое для кодирования всех 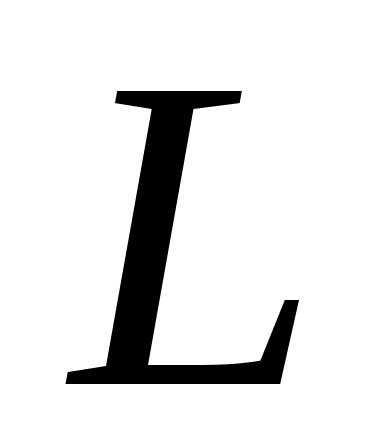 всех уровней квантованного сообщения. Запишите комбинацию примитивного двоичного кода, которая соответствует передаче уровня квантованного сообщения с номером всех уровней квантованного сообщения. Запишите комбинацию примитивного двоичного кода, которая соответствует передаче уровня квантованного сообщения с номером 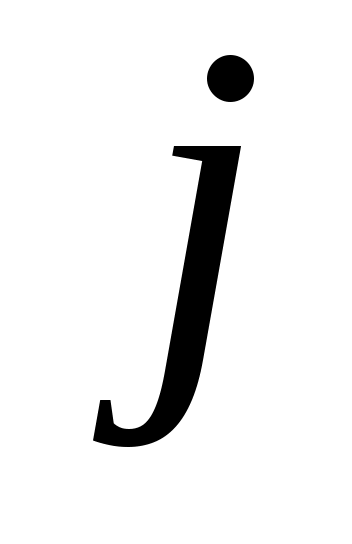 , считая, что кодовая комбинация представляет собой запись числа , считая, что кодовая комбинация представляет собой запись числа 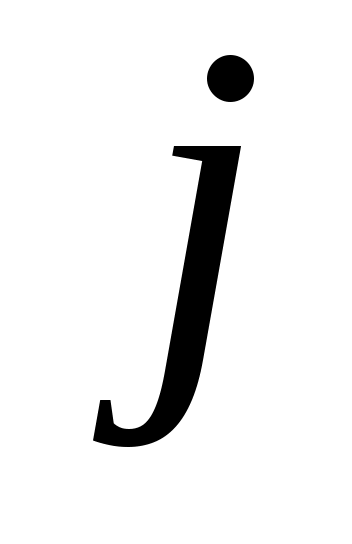 в двоичной системе счисления. Постройте порождающую матрицу кода в двоичной системе счисления. Постройте порождающую матрицу кода 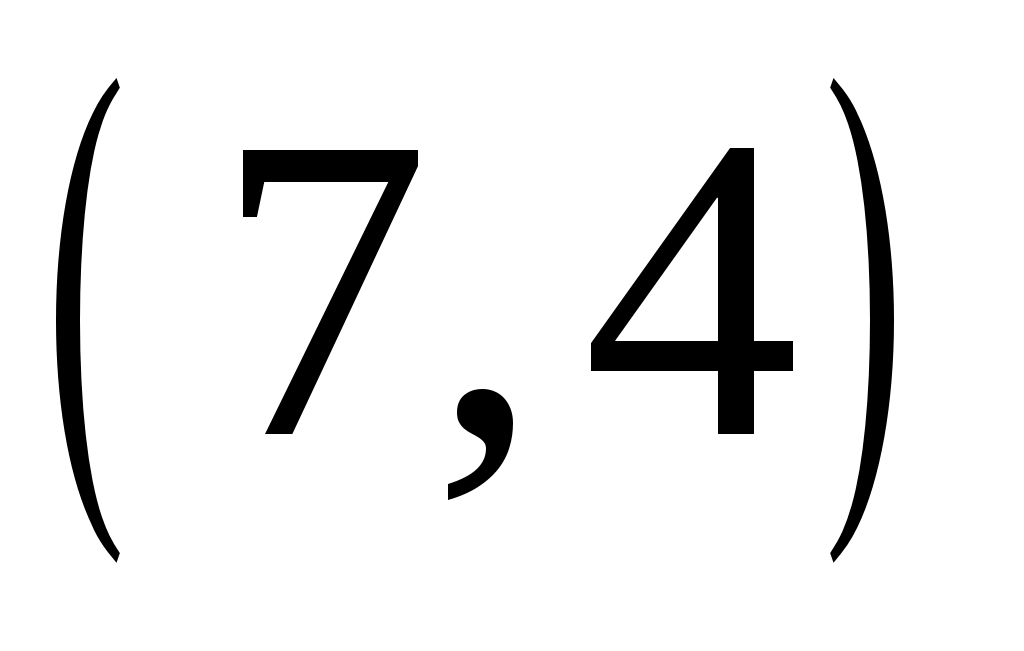 . Правила формирования проверочных разрядов необходимо выбрать из таблицы 2 по последней цифре зачетной книжки. Используя порождающую матрицу, составить разрешенные кодовые комбинации кода . Правила формирования проверочных разрядов необходимо выбрать из таблицы 2 по последней цифре зачетной книжки. Используя порождающую матрицу, составить разрешенные кодовые комбинации кода 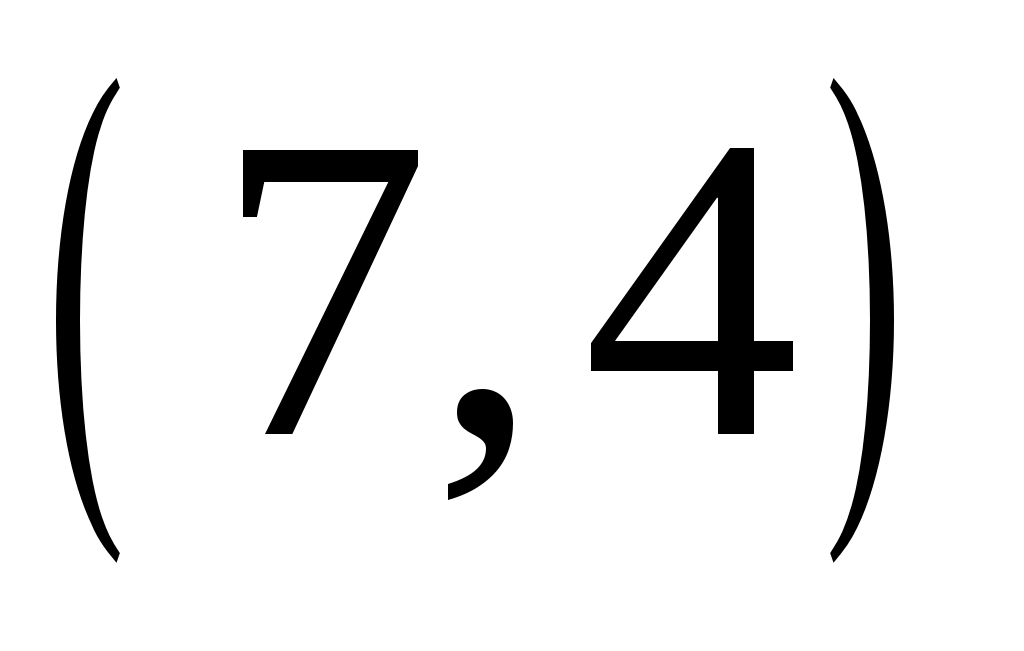 . Закодируйте передаваемый уровень квантования . Закодируйте передаваемый уровень квантования 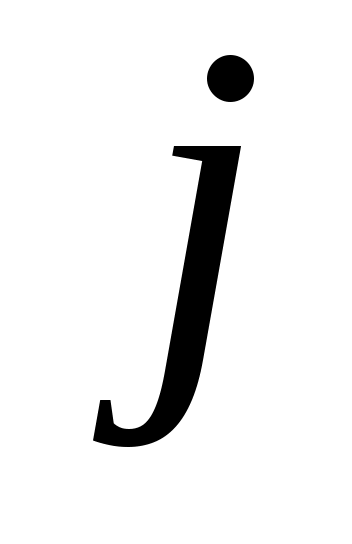 кодом кодом 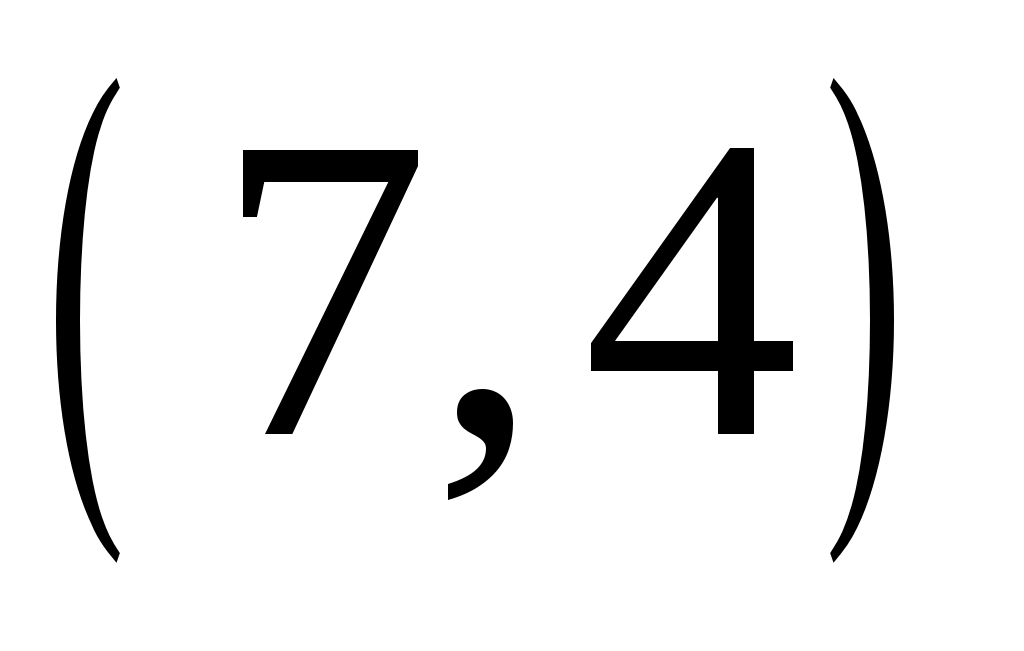 . .
Запишите аналитическое выражение модулированного сигнала 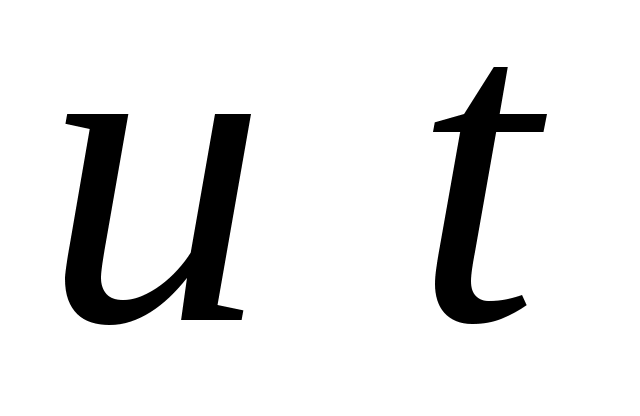 , связывающее его с первичным сигналом , связывающее его с первичным сигналом 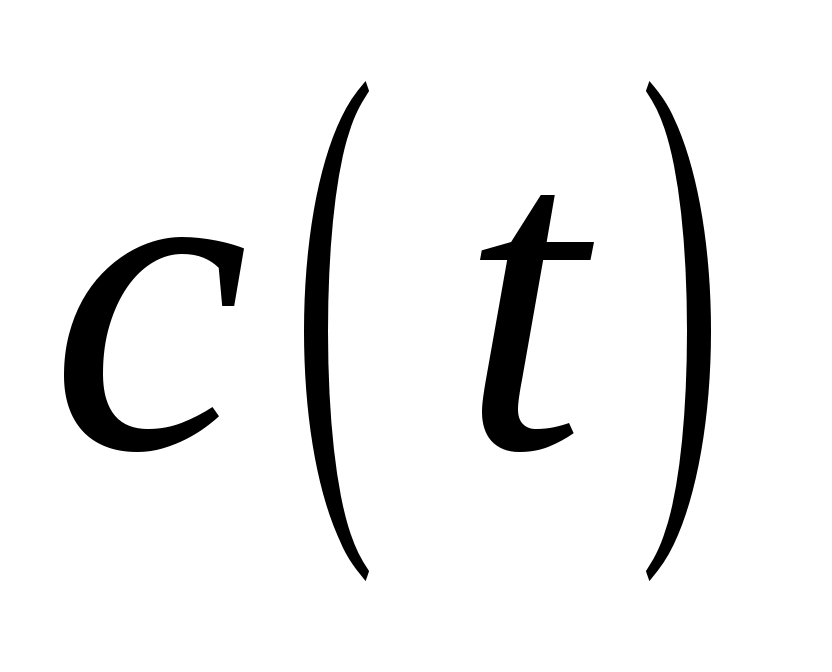 . Определите ширину полосы частот модулирующего (первичного) сигнала . Определите ширину полосы частот модулирующего (первичного) сигнала 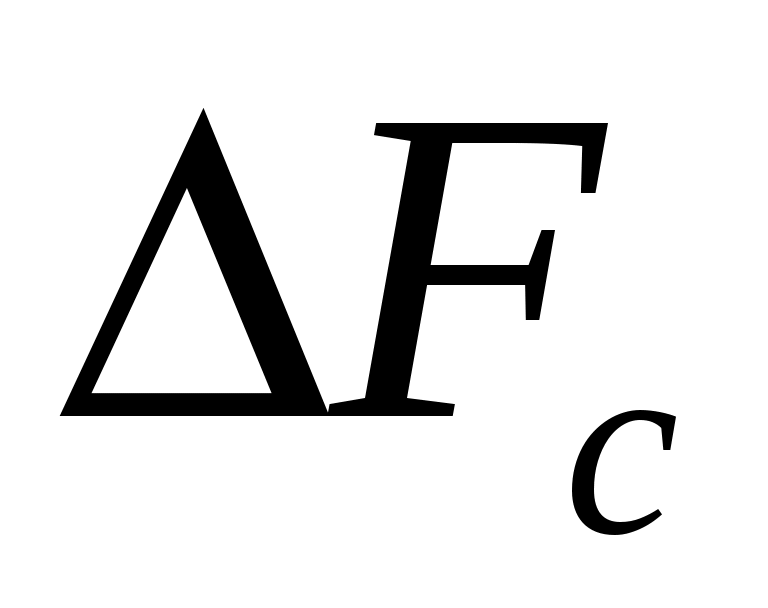 .Определите полосу частот модулированного сигнала .Определите полосу частот модулированного сигнала 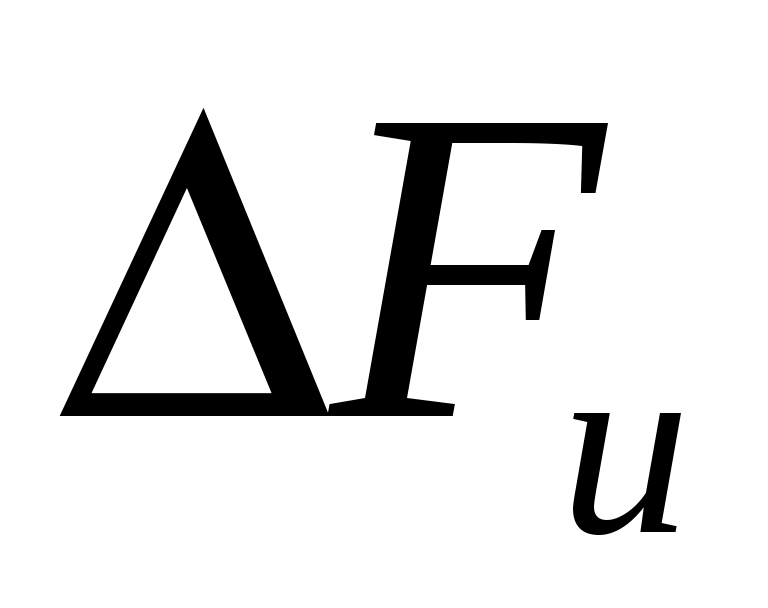 . .
Запишите аналитическое выражение для случайного процесса на выходе канала 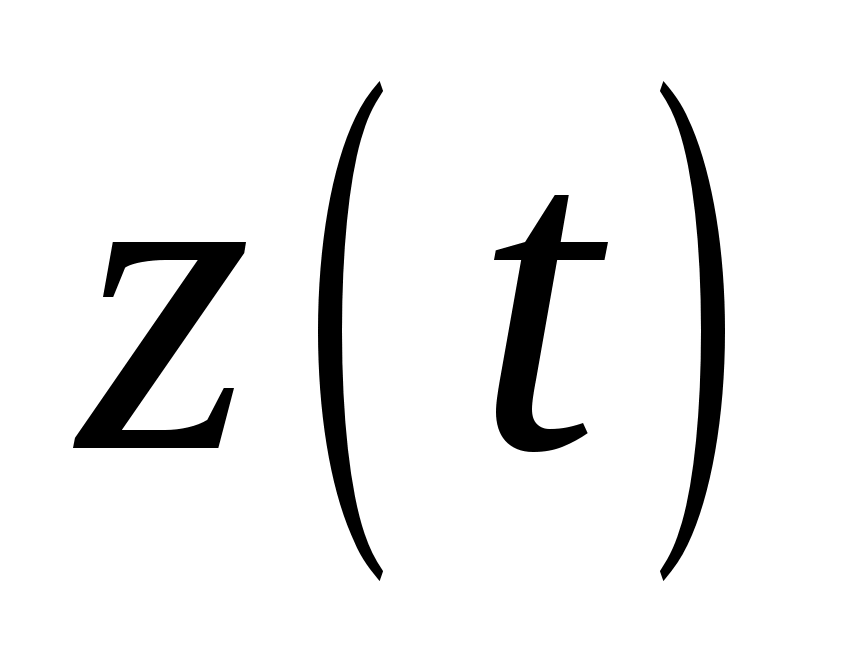 . Найдите мощность белого шума на выходе канала . Найдите мощность белого шума на выходе канала 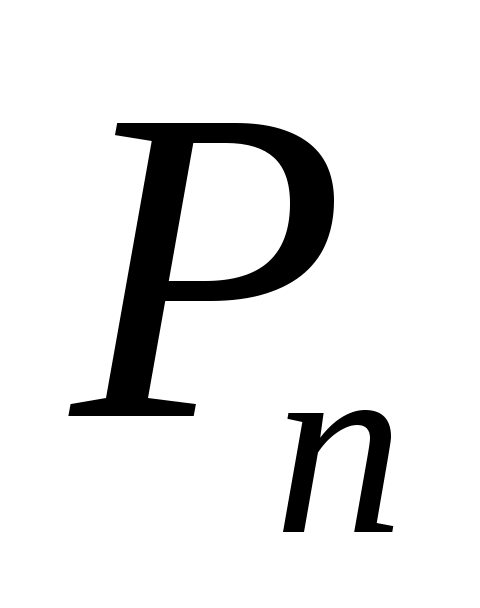 . Определите среднюю мощность сигнала на выходе канала . Определите среднюю мощность сигнала на выходе канала 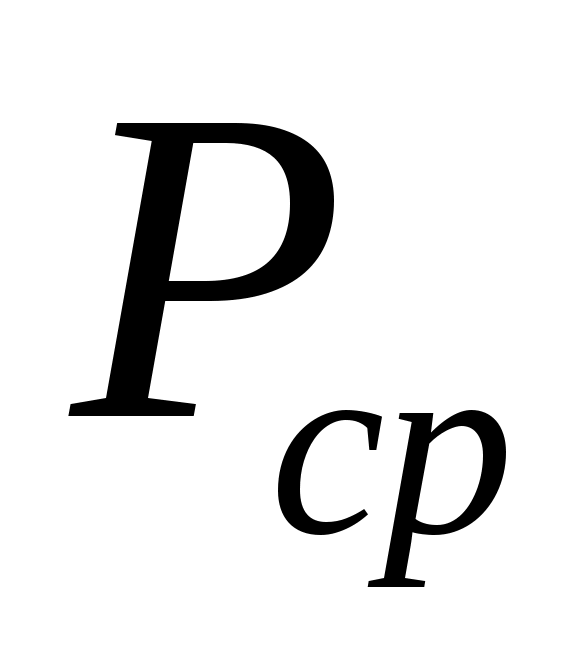 . Найдите отношение средней мощности сигнала к мощности шума на выходе канала . Найдите отношение средней мощности сигнала к мощности шума на выходе канала 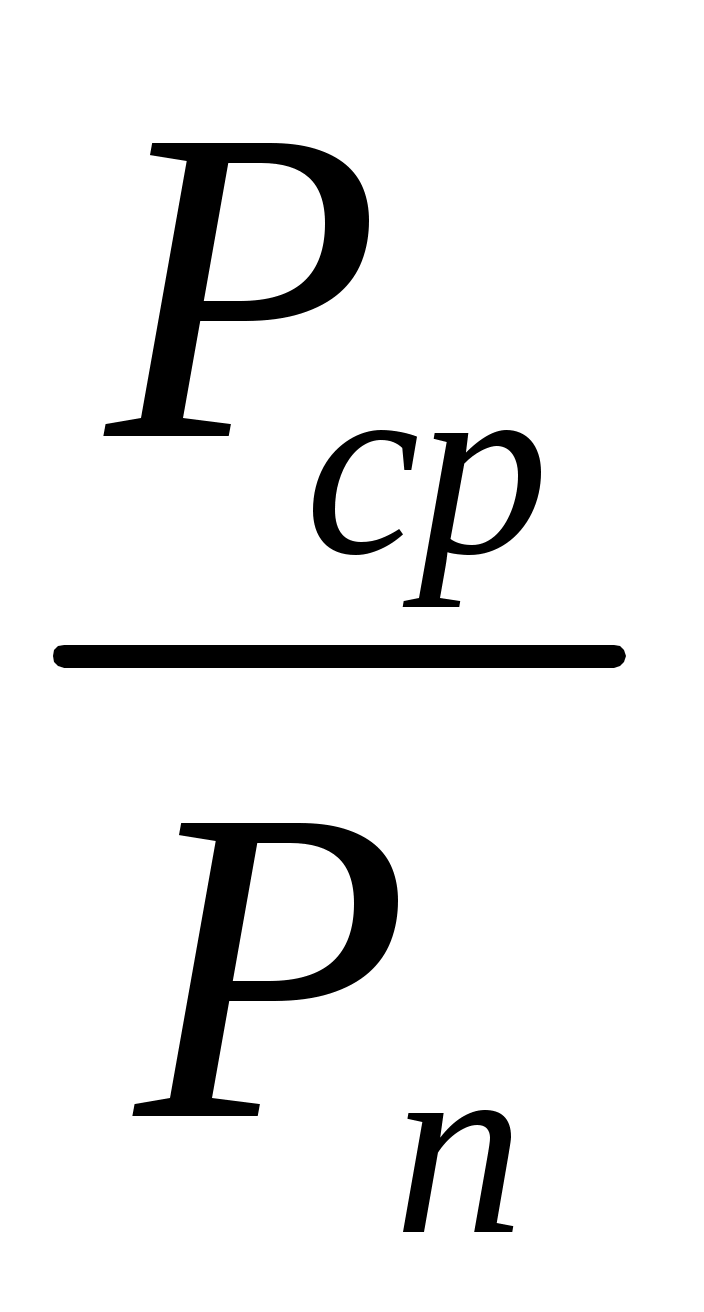 . Вычислите пропускную способность гауссовского непрерывного канала . Вычислите пропускную способность гауссовского непрерывного канала 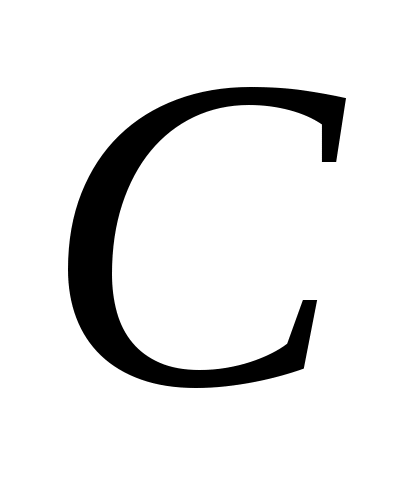 . Определите коэффициент эффективности использования пропускной способности канала . Определите коэффициент эффективности использования пропускной способности канала 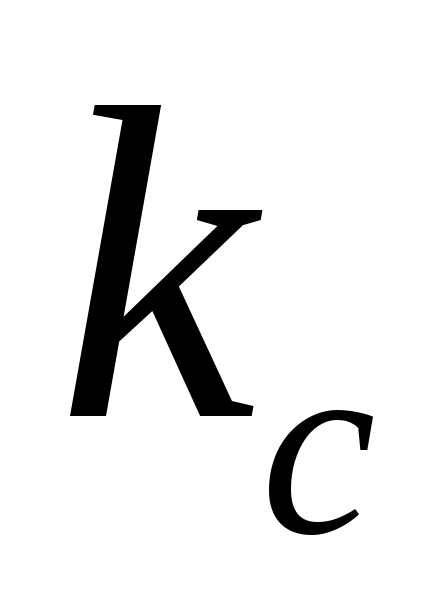 . .
Запишите общее правило приема оптимального когерентного демодулятора при точно известных двоичных сигналах, полагая, что сигналы равновероятны. Запишите алгоритм работы оптимального когерентного демодулятора двоичных сигналов с заданным видом модуляции в канале с белым гауссовским шумом. Вычислите эквивалентную энергию системы сигналов при заданном способе модуляции. Рассчитайте среднюю вероятность ошибки демодулятора 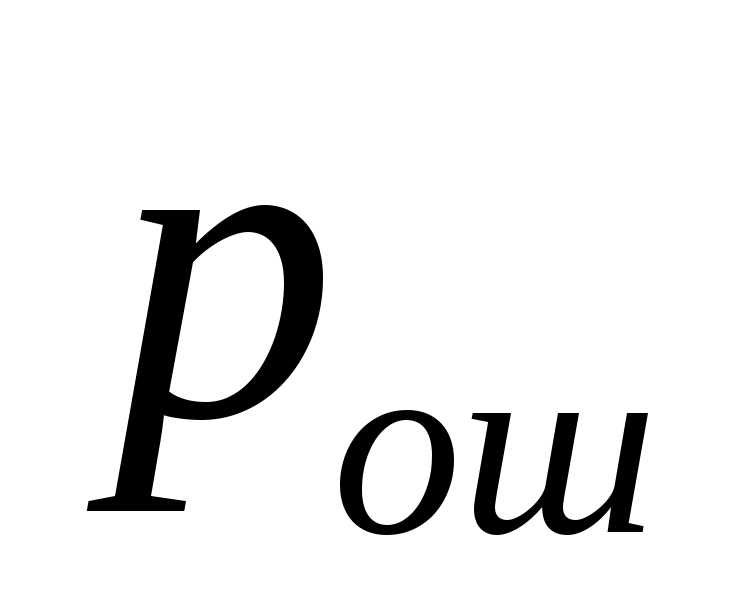 . Определите, каким образом необходимо изменить энергию сигналов, чтобы при других видах модуляции и заданном способе приема сохранялось бы тоже значение вероятности ошибки . Определите, каким образом необходимо изменить энергию сигналов, чтобы при других видах модуляции и заданном способе приема сохранялось бы тоже значение вероятности ошибки 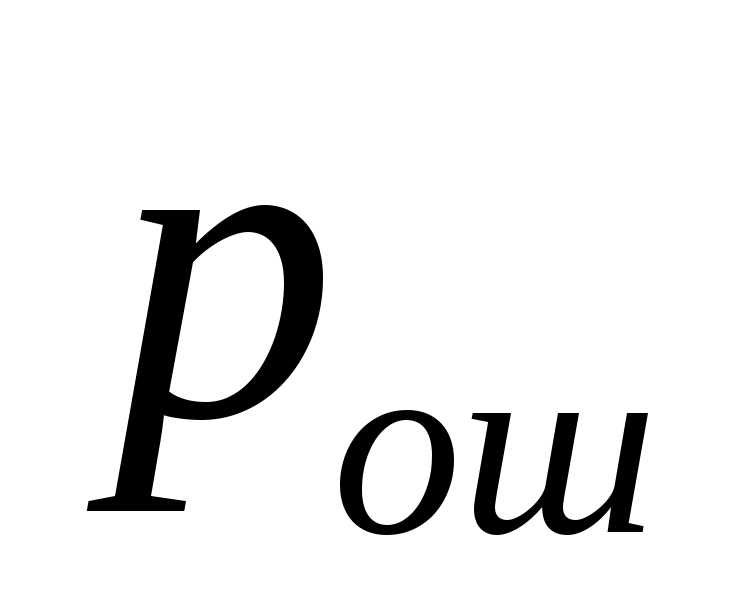 . .
Постройте проверочную матрицу определенного ранее кода. Постройте таблицу синдромов для всех возможных вариантов одиночных ошибок. Вычислите синдром одной из кодовых комбинаций кода 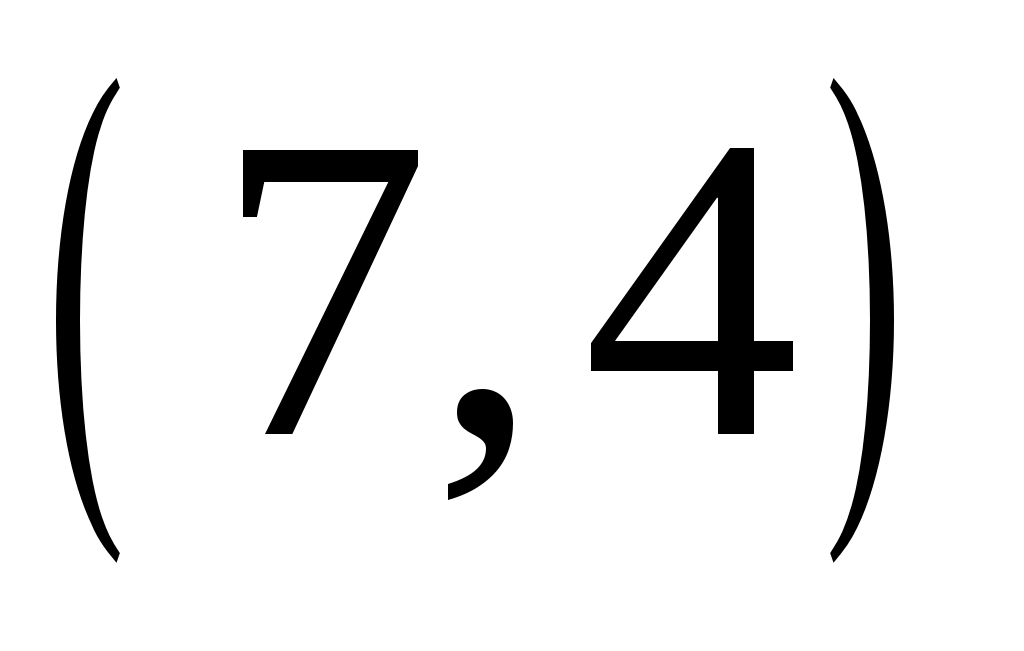 . Введите одиночную ошибку в разряд, номер которой совпадает с последней цифрой зачетной книжки . Введите одиночную ошибку в разряд, номер которой совпадает с последней цифрой зачетной книжки 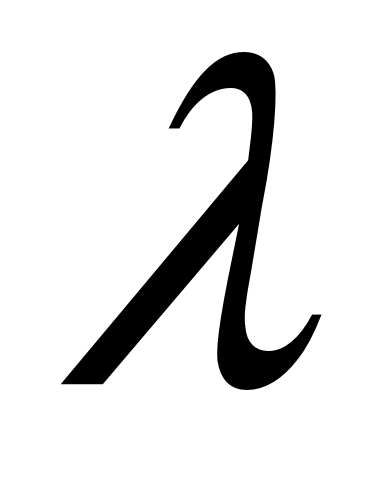 если она равна 1 ,2 ,3 ,4 ,5 6, 7. Если последняя цифра если она равна 1 ,2 ,3 ,4 ,5 6, 7. Если последняя цифра 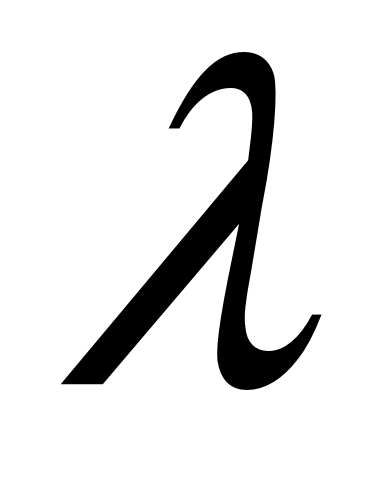 равна 8, 9, 0, то ошибку следует ввести в разряд, номер которого равен равна 8, 9, 0, то ошибку следует ввести в разряд, номер которого равен 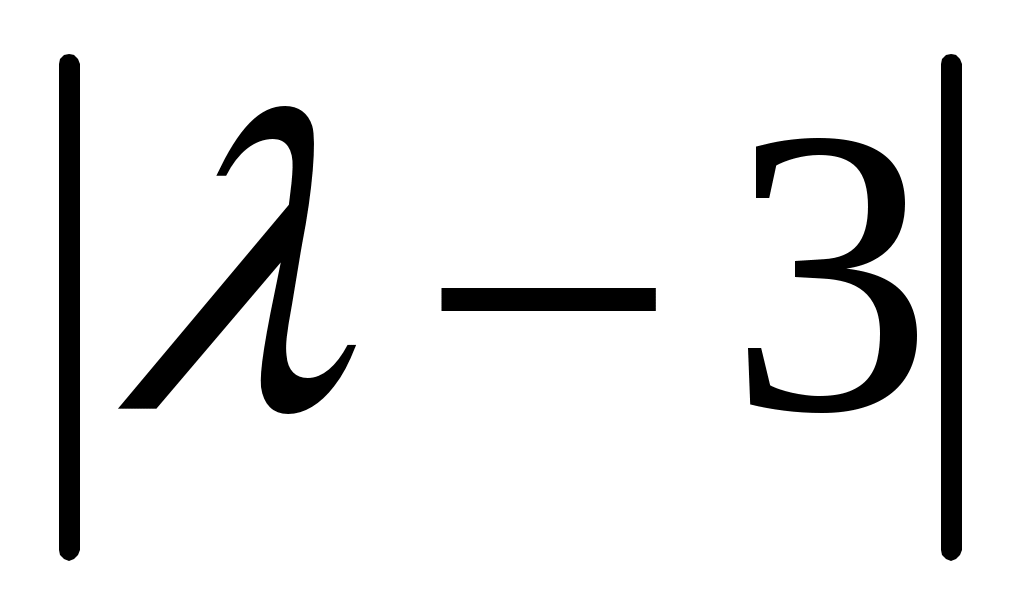 . Вычислите синдром и исправьте ошибку, инвертировав ошибочный символ. Вычислите синдром и исправьте ошибку, инвертировав ошибочный символ. Определите вероятность необнаруженной ошибки при использовании кода . Вычислите синдром и исправьте ошибку, инвертировав ошибочный символ. Вычислите синдром и исправьте ошибку, инвертировав ошибочный символ. Определите вероятность необнаруженной ошибки при использовании кода 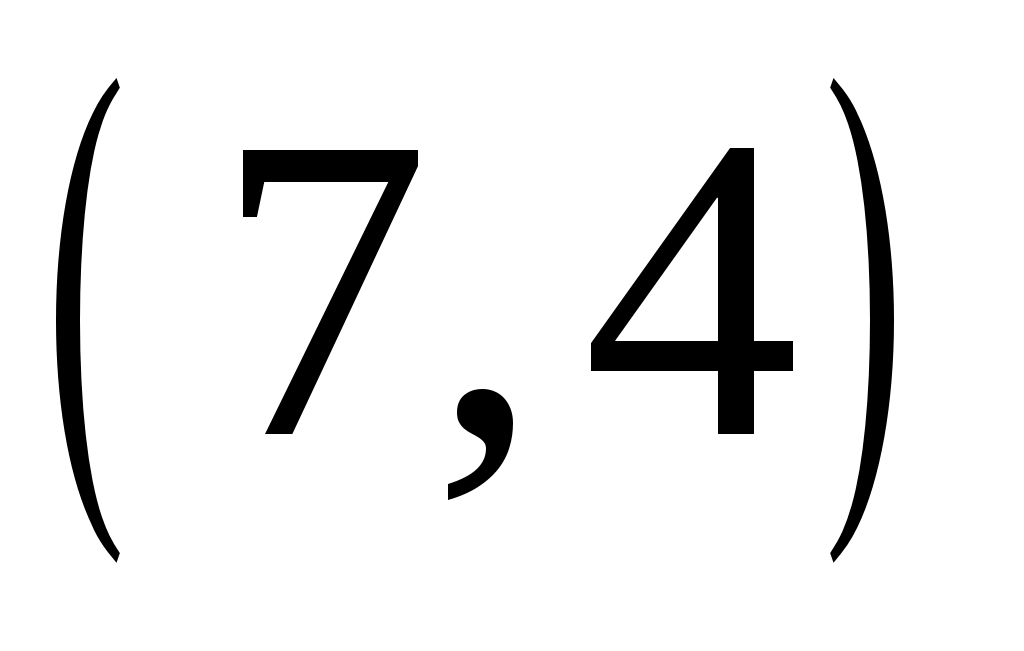 в режиме обнаружения ошибок. Определите вероятность ошибочного декодирования при использовании кода в режиме обнаружения ошибок. Определите вероятность ошибочного декодирования при использовании кода 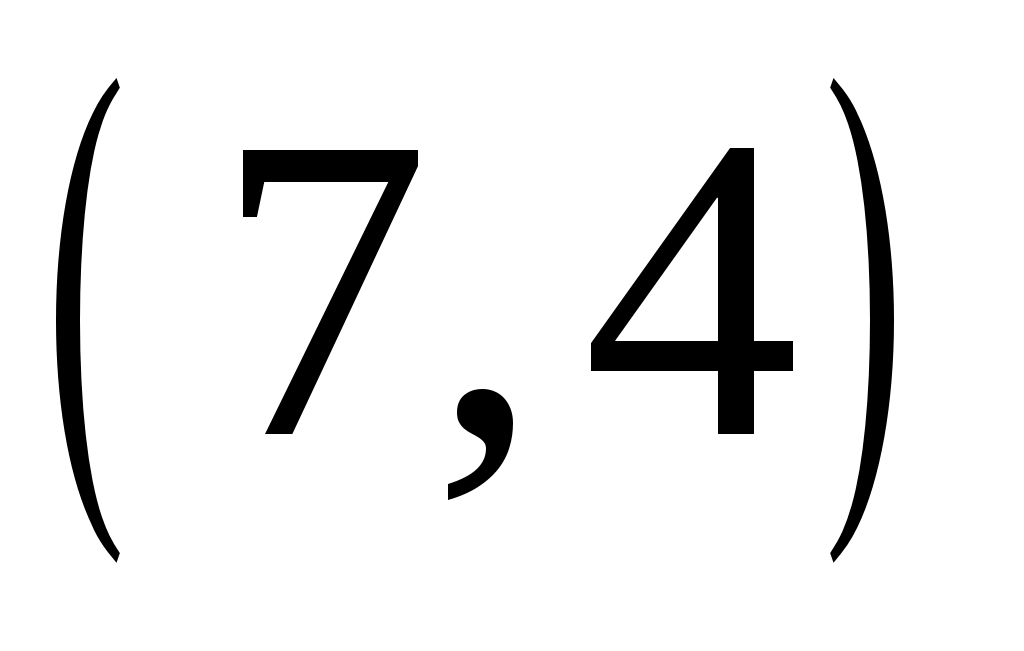 в режиме исправления ошибок. в режиме исправления ошибок.
Укажите значение 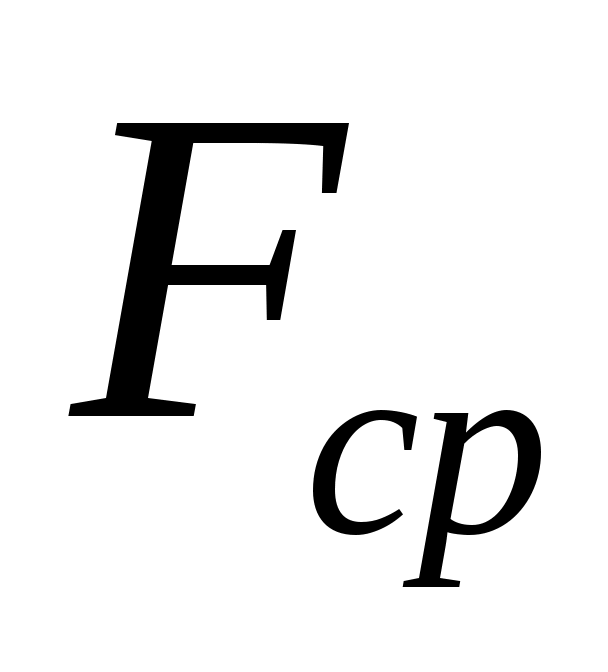 , при котором обеспечивается теоретически точное восстановление непрерывного сообщения. Запишите аналитическое выражение амплитудно-частотной характеристики , при котором обеспечивается теоретически точное восстановление непрерывного сообщения. Запишите аналитическое выражение амплитудно-частотной характеристики 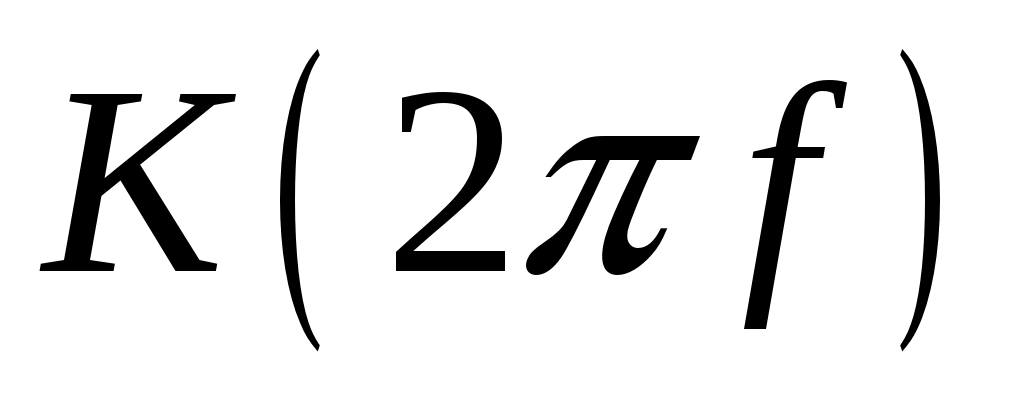 фильтра восстановителя. Найдите импульсную характеристику фильтра восстановителя. Найдите импульсную характеристику 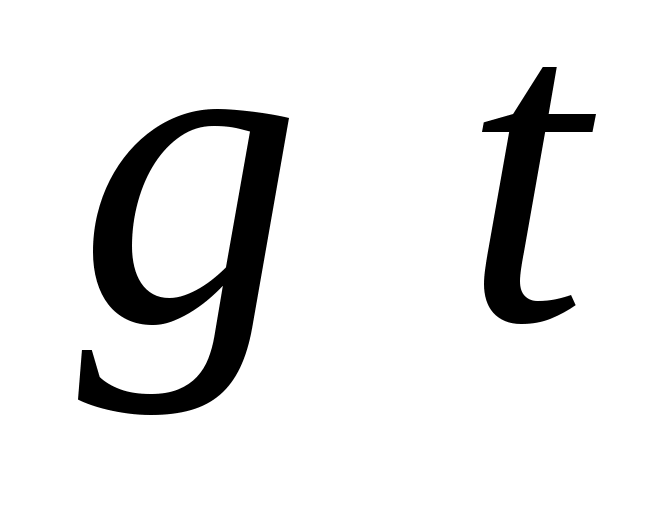 фильтра-восстановителя. фильтра-восстановителя.
Таблица 2. – Таблица кода 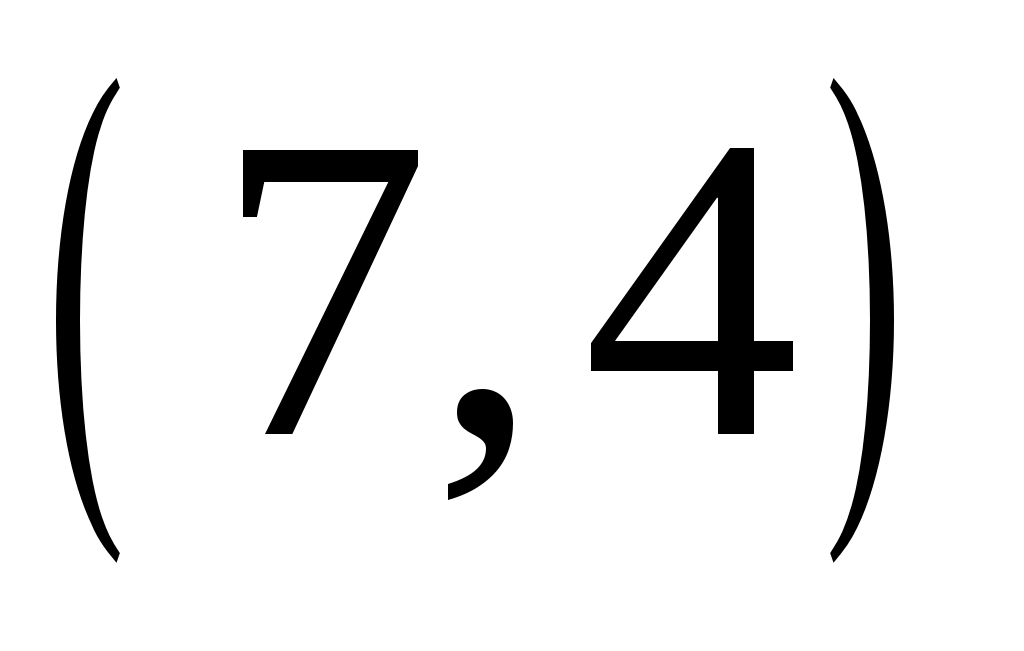
Номер разрешенной комбинации
|
Разрешенная кодовая комбинация
|
Суммируемые строки порождающей матрицы
|
1
|
0000000
|
Любая сама с собой
|
2
|
1000110
|
Первая
|
3
|
0100101
|
Вторая
|
4
|
0010111
|
Третья
|
5
|
0001011
|
Четвертая
|
6
|
1100011
|
Первая и вторая
|
7
|
1010101
|
Первая и третья
|
8
|
1001111
|
Первая и четвертая
|
9
|
0110010
|
Вторая и третья
|
10
|
0101111
|
Вторая и четвертая
|
11
|
0011100
|
Третья и четвертая
|
12
|
1110100
|
Первая, вторая и третья
|
13
|
1101000
|
Первая, вторая и четвертая
|
14
|
1011010
|
Первая, третья и четвертая
|
15
|
0111001
|
Вторая, третья и четвертая
|
16
|
1111111
|
Первая, вторая, третья и четвертая
| |
 Скачать 348 Kb.
Скачать 348 Kb.