Расчет цилиндрической
 Скачать 90.4 Kb. Скачать 90.4 Kb.
|
|
` РАСЧЕТ ЦИЛИНДРИЧЕСКОЙ
ЗУБЧАТОЙ ПРЯМОЗУБОЙ ПЕРЕДАЧИ Исходные данные: 1 Угловая скорость ведущего и ведомого валов 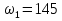 и и 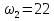 , рад/c; , рад/c;2 Мощность на ведущем валу 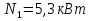 ; ;3 Условия работы передачи  Порядок расчета: 1 Передаточное отношение передачи, i определяем по формуле 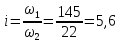 (1) (1)где 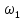 – угловая скорость ведущего колеса, – угловая скорость ведущего колеса, 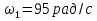 ; ;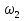 – угловая скорость ведомого колеса, – угловая скорость ведомого колеса, 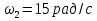 . .2 Вращающий момент на валу шестерни, 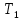 , Нм определяем по формуле , Нм определяем по формуле 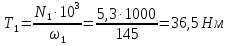 (2) (2)где 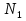 – мощность на ведущем валу, – мощность на ведущем валу, 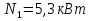 3 Для изготовления зубчатой передачи выбираем низколегированную улучшаемую сталь 40Х с содержанием углерода 0,4%, хрома 1 –1,5% Твердость шестерни принимаем НВ1=282, твердость колеса НВ2=260. Механические характеристики: Предел прочности, 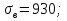 Предел текучести, 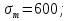 Предел временной прочности, 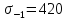 4 Число циклов нагружения колес, 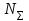 определяем по формуле определяем по формуле для шестерни: 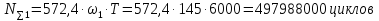 (3) (3)для колеса: 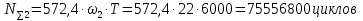 (4) (4)
где: ω- вала, ω1=145рад/c, ω2= 15,рад/с; Т–срок службы передачи, Т=6000ч. Базовое число циклов нагружения по контактным напряжениям определяем интерполяцией. Для шестерни при твердости НВ1=282: 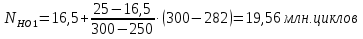 (5) (5)Для колеса при твердости НВ2=260: 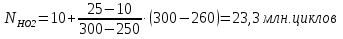 (6) (6)5 Коэффициент долговечности по контактным напряжениям для шестерни и колеса, определяем по формуле Для шестерни 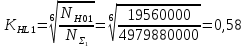 (7) (7)Принимаем 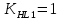 Для колеса 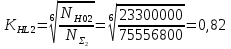 (8) (8) Принимаем 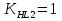 6 Коэффициент долговечности по напряжениям изгиба для шестерни и колеса, определяем по формуле для шестерни 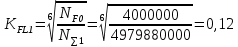 (9) (9)Принимаем 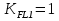 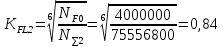 (10) (10)
Принимаем 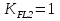 7 Определяем значения пределов выносливости 7.1 Контактной для зубьев колеса 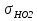 , Мпа по формуле , Мпа по формуле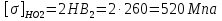 (11) (11)7.2 Изгибной для зубьев шестерни 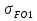 , Мпа по формуле , Мпа по формуле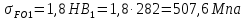 (12) (12)7.3 Изгибной для зубьев колеса 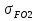 , Мпа по формуле , Мпа по формуле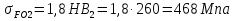 (13) (13)8.Определяем допускаемые напряжения 8.1 Контактные для материала колеса, как менее прочного определяем по формуле 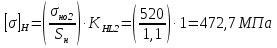 (14) (14) где Sн – коэффициент безопасности; Sн=1,1 8.2 Изгибные для материала колеса и шестерни определяем по формуле Для шестерни 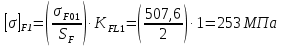 (15) (15)Для колеса 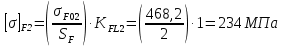 (16) (16)где SF – коэффициент безопасности, SF=2 9 Межосевое расстояние, 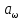 , мм, определяем по формуле , мм, определяем по формуле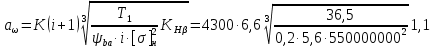 (17) (17)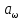 = 0,148м = 0,148м где К – коэффициент, К=4300; i - передаточное отношение, i=5,6; T1- вращающий момент на валу шестерни, Нм, T1 = 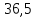 Нм; Нм; 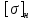 - допускаемое кантактное напряжение для материала колеса, Па; - допускаемое кантактное напряжение для материала колеса, Па;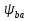 - коэффициент ширины венца колеса, - коэффициент ширины венца колеса,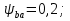 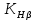 – коэффициент нагрузки, – коэффициент нагрузки, 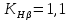
Межосевое расстояние принимаем 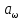 = 148 мм = 148 мм10 Модуль зацепления, m, мм, определяем по формуле m 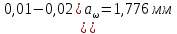 (18) (18)Модуль зацепления принимаем за m = 2 мм Принимаем угол наклона зубьев 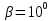 11 Определяем число зубьев 11.1 Суммарное по формуле 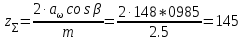 (19) (19)Принимаем 145 зубьев 11.2 Число зубьев шестерни, z1, определяем по формуле 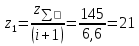 ,9 (20) ,9 (20)Принимаем 22 зуба 11.3 Число зубьев колеса, z2, определяем по формуле 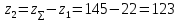 (21) (21)Уточняем угол наклона зубьев 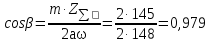 (22) (22)Угол наклона зубьев 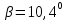 12 Передаточное число,u, определяем по формуле 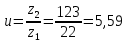 (23) (23)Определяем отклонение передаточного числа от передаточного отношения 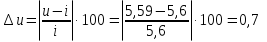 (24) (24)Отклонение меньше 4% следовательно количество зубьев подобрано верно. 13 Определение геометрических размеров шестерни и колеса
13.1 Диаметр делительных окружностей, d1 и d2 мм, определяем по формуле 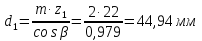 (25) (25) 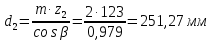 (26) (26) 13.2 Диаметр окружностей вершин, da1 и da2, мм, определяем по формуле 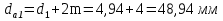 (27) (27) 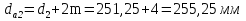 (28) (28)13.3 Диаметр окружностей впадин, df1 и df2, мм, определяем по формуле 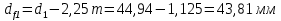 (29) (29)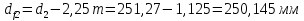 (30) (30)13.4 Ширина венца колеса , b2, мм, определяем по формуле 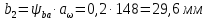 (31) (31)13.8 Ширина венца шестерни,b1 ,мм , определяем по формуле 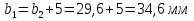 (32) (32)14 Окружную скорость шестерни, v, м/c, определяем по формуле 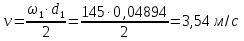 (33) (33)где: 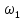 – угловая скорость вала шестерни, – угловая скорость вала шестерни, 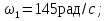 d1– делительный диаметр шестерни, d1=0,048 м 15 Окружную силу передачи, Ft, Н, определяем по формуле 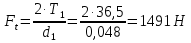 (34) (34)
16 Расчетные контактные напряжения, 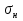 , Па, определяем по формуле , Па, определяем по формуле 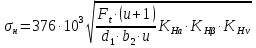 (35) (35)где 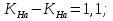 коэффициент, учитывающий распределение нагрузки между коэффициент, учитывающий распределение нагрузки между зубьями 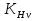 - коэффициент динамической нагрузки, - коэффициент динамической нагрузки,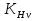 =1 =1 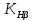 - коэффициент нагрузки, - коэффициент нагрузки, 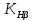 = 1,1 = 1,1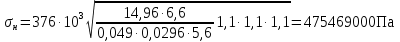 Отклонение от допускаемого значения находится по формуле  (36) (36)Перегрузка передачи 0,5%, что не превышает допустимого значения, следовательно работоспособность передачи обеспечена. 17 Определяем расчетное напряжения изгиба 17.1 Эквивалентное число зубьев шестерни, zv1 и zv2, определяем по формуле 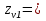 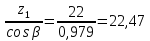 (37) (37)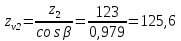 (38) (38)17.2 Определяем коэффициенты формы зуба 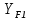 и и 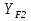 принимаем 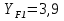 , , 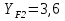 17.3 Сравнительные характеристики прочность зубьев на изгиб для шестерни определяем по формуле 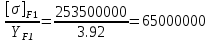 (39) (39)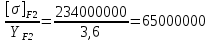 (40) (40) 17.4 Расчетные напряжения изгиба для колеса как менее прочного звена определяем по формуле 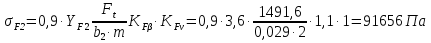 (41) (41)Расчетные напряжения меньше допускаемых. Прочность зуба колеса на изгиб обеспечена.
|
