Расчет физических параметров оптического волокна. Расчет физических параметров оптического волокна
 Скачать 71.99 Kb.
|
|
Расчет физических параметров оптического волокна Для изготовления оптических волокон, используемых в диапазоне  = 0,8…1,8 мкм, применяются кварцевые стекла с легирующими добавками окиси германия GeO2, фосфора P2O3 повышающими показатель преломления кварца добавками окиси бора B2O3, фтора F, понижающими его показатель преломления. В таблице 2.1 представлены Коэффициенты ряда Селмейера для кварцевых стекол согласно варианта задания на курсовую работу.Таблица 2.1 - Коэффициенты ряда Селмейера для кварцевых стекол
Исходя из коэффициентов Селмейера, можно рассчитать показатель преломления для данного состава стекла по формуле:  , (2.1)где - длина волны, мкмТаким образом, подставив табличные значения в формулу получим: 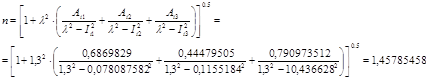 n2 = 1,45785458 С учетом того, что в данной работе рассчитывается одномодовое волокно, для него имеет место условие:  . (2.2)Таким образом, исходя из данного условия, найдем n1:  Получив значения n1 и n2 теперь можно найти относительную разность показателей преломления (  ): (2.3)Еще статьи Аналого-цифровой преобразователь 1. Расчет фильтра для схемы Аналого-цифрового преобразователя(АЦП). 2. Расчет источника опорного напряжения для схемы АЦП. . Выбор компаратора. . Составление счетчика или выбор готового. . Составление схемы генератора прямоугольных импульсов. . ... Условием существования направляемой моды является экспоненциальное убывание ее поля в оболочке вдоль координаты r, причем степень уменьшения напряженности с ростом r определяется значением n, уменьшение которой приводит к перераспределению поля в оболочку OB – появлению вытекающих волн. При n=0 происходит качественное изменение волнового процесса, заключающегося в невозможности существования направляемой моды. Этот режим называется критическим, в связи с чем очень важно определение условий его возникновения. Сделаем подстановку в последнее уравнение значения n=0, в результате правые части уравнений обращаются в бесконечность и для Е и Н мод будет справедливо условие  (2.13)которое определяет границы их возникновения или исчезновения. Последнее уравнение имеет бесчисленное множество решений, поэтому, обозначив положительный корень через P0m, а также используя выражения для c и n, получаем  ,Введем величину, которая носит название нормированной частоты:  . (2.14)Это один из важнейших обобщающих параметров, используемых для оценки свойств ОВ, который связывает его структурные параметры и длину световой волны, распространяемой в волокне. Тогда  , и при n=0 для каждого из корней имеет место критическое значение нормированной частоты:P0m = cкрR = V0m, где m=1,2,3,...m, (2.15) а P01 =2.405; P02= 5.520; P03= 8.654 и т. д. Если для некоторой симметричной моды нормированная частота больше ее критического значения (V > V0m), то она распространяется в ОВ, в противном случае ее нет. Последняя формула позволяет определить значения критических длин волн l0mкр для симметричных волн в волокне 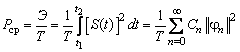 , (2.16)или, переходя к частоте,  . (2.17)Очевидно, что для распространяющейся моды должно выполняться условие  , т. е.  , в противном случае этой моды нет.В отличие от симметричных мод несимметричные имеют все шесть составляющих векторов электромагнитного поля и их невозможно разделить на электрические и магнитные. Критическая нормированная частота в этом случае определяется выражением Vnm = Pnm , n=1,2, 3 ... N; т = 1, 2, 3,... М, (2.18) в результате чего при заданных параметрах ОВ критическая длина волны равна  , (2.19)где Pnm – положительный корень соответствующего трансцендентного уравнения: для HE1m моды  для HE1m моды  для HEnm моды  (3.20)для HEnm моды  .Указанные уравнения также получены из основного дисперсионного уравнения при n=0. Среди направляемых мод особое положение занимает мода, у которой критическое значение нормированной частоты V11=0. Это основная (фундаментальная) мода ступенчатого ОВ, так как она распространяется при любой частоте и структурных параметрах волокна. С точки зрения геометрической оптики, она образуется лучом, вводимым вдоль оси волокна, так как только характеристики такого луча не зависят от условий отражения на границе «сердцевина – оболочка». Выбирая параметры ОВ, можно получить режим распространения только этой моды, что реализуется при условии  , (2.21)Минимальная длина волны, при которой в волокне распространяется фундаментальная мода, называется волоконной длиной волны отсечки, значение которой легко определяется из последнего выражения как  . (2.22)На практике больший интерес представляет так называемая кабельная длина волны отсечки  .При увеличении нормированной частоты в ОВ появляются другие моды, которые принято называть высшими. Каждая из этих мод обладает характерной для нее структурой электромагнитного поля в сердцевине и оболочке, а также запаздыванием по фазе j, которое для симметричных и несимметричных мод определяется в результате численного решения соответствующих дисперсионных уравнений. На практике вместо дисперсионных характеристик b = f(w) удобнее использовать нормированные дисперсионные параметры b/k0 = f(V), которые описывают свойства всех ступенчатых ОВ. При определенной длине волны наступает такой режим, при котором q = 0°, и волна, падая на границу "сердцевина – оболочка", отражается от нее под прямым углом. В этом случае в ОВ устанавливается режим стоячей волны, и энергия вдоль волокна не распространяется, что соответствует случаю критической длины волны. Поэтому по ОВ возможна передача электромагнитного излучения только с длиной волны, меньшей диаметра волокна, т.е. l< d. 2.4. Частотное и пространственное изменения показателя преломления Категория: 2. Физические основы передачи электромагнитной энергии по оптическим волокнам Внутри волновых пакетов отдельные волны распространяются с различными скоростями благодаря их различным длинам. Скорость распространения такого волнового пакета называется групповой скоростью. Определен и соответствующий групповой показатель преломления ng, который соотносится с показателем преломления следующим образом ng = n –l  . (2.4.1)На рисунке 2.5 показаны кривые для n и ng для чистого кварцевого стекла в зависимости от длины волны l.  В таблице 2.1 представлены некоторые численные значения n(l) и ng(l) для кварца. Таблица 2.1 – Показатель преломления n(l) и групповой показатель преломления ng(l)
Выражение dn/dl дает наклон кривой показателя преломления n(l), который в рассматриваемом диапазоне длин волн является нисходящим (отрицательным). Поэтому групповой показатель преломления ng при любой длине волны больше показателя преломления n. Для расчетов времени передачи оптических сигналов следует использовать только групповой показатель преломления ng. Полезно отметить, что групповой показатель преломления достигает своего минимума вблизи длины волны 1300 нм. Этот диапазон длин волн является особенно интересным для оптической связи. Если рассматривать показатель преломления n волоконного световода как функцию от радиуса r, то используется термин профиль распределения показателя преломления. С его помощью описывается радиальное изменение показателя преломления от оси волокна в стекле сердцевины в направлении стекла оболочки: n=n(r). Распределение мод в волоконном световоде зависит от формы этого профиля распределения показателя преломления (рисунок 2.6).  Для практического применения важными являются «профили распределения показателя преломления, описываемые по степенному закону» (степенные профили). Под ними понимаются профили показателя преломления, у которых кривая изменения по радиусу описывается как степенная функция радиуса:  , для r < a (в сердцевине) (2.4.2)и n2(r)=n22 = постоянная , для r ³ a (в оболочке) (2.4.3) где n0- показатель преломления в центре сердцевины; n1- показатель преломления вдоль оси оптического волокна; D- нормированная разность показателей преломления; r - расстояние от оси оптического волокна, мкм; a - радиус сердцевины, мкм; u- показатель степени профиля; n2- показатель преломления оболочки. Нормированная разность показателей преломления соотносится с числовой апертурой NA или показателями преломления n1 и n2 следующим образом D = (NA)2 / 2 n21 = (n21 - n22) / 2 n21 . (2.4.4) Отметим особые случаи (рисунок 2.6): u = 1 – треугольный профиль u = 2 – параболический профиль u ®¥– ступенчатый профиль (предел величины u - бесконечность). Лишь в последнем случае – при ступенчатом профиле – показатель преломления n(r)=n1 в стекле сердцевины остается постоянным. Для всех других профилей показатель преломления n(r) в стекле сердцевины постепенно увеличивается от n2 для стекла оболочки до n1 у оси волоконного световода. Поэтому такие профили называют градиентными профилями распределения показателя преломления. Это название особенно хорошо закрепилось за параболическим профилем, имеющим u=2, оптические волокна с таким профилем имеют технически очень хорошие характеристики передачи света. | ||||||||||||||||||||||||||