Главная страница
Навигация по странице:

  • Решение 1. Элементы 2, 3

    		•

    Расчет надежности технической системы


    Скачать 420.5 Kb.
    НазваниеРасчет надежности технической системы
    Дата18.04.2022
    Размер420.5 Kb.
    Формат файлаdoc
    Имя файлаopisanie_RGR_6_VARIANT.doc
    ТипДокументы
    #482054

    МИНОБРНАУКИ РОССИИ

    Федеральное государственное бюджетное образовательное учреждение


    высшего профессионального образования

    «Тверской Государственный Технический Университет»



    Расчетно-графическая работа

    по курсу «Надежность и эффективность ЭИС»

    на тему:

    «Расчет надежности технической системы»

    Вариант №6


    Выполнил: студент 5-го курса

    группы ПИЭ 0708 Кочнова Т.А.

    Принял: Егерева И.А.

    Тверь, 2011 г.

    Исходные данные

    По структурной схеме надежности технической системы (рис. 1) требуемому значению вероятности безотказной работы системы и значениям интенсивностей отказов ее элементов (табл. 1) требуется:

    1. Построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1 - 0.2.

    2. Определить - процентную наработку технической системы.

    3. Обеспечить увеличение - процентной наработки не менее, чем в 1.5 раза за счет:

    а) повышения надежности элементов;

    б) структурного резервирования элементов системы.

    Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными.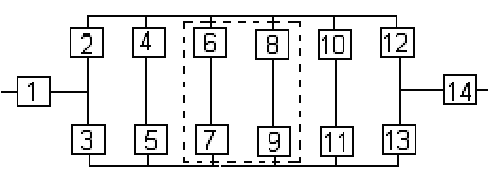



    Рис. 1. Структурная схема надежности технической системы

    Таблица 1

    Численные значения параметров

    γ, %
    Интенсивности отказов элементов, 𝛌 i , x10-6 1/ч

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15

    75
    0,2
    0,7
    0,65
    0,7
    0,6
    -

    Решение

    1. Элементы 2, 3 образуют последовательное соединение, которое заменяем соответственно квазиэлементом A.

    Учитывая, что p2=p3 , то получим следующую формулу:

    PA= p2*p3=p22 (1)

    2. Элементы 4 и 5 образуют последовательное соединение, которое заменяем соответственно квазиэлементом B.

    Учитывая, что p4=p5, то получим следующую формулу:

    PB=p4*p5= p42 (2)

    3. Элементы 6, 7 образуют последовательное соединение, которое заменяем соответственно квазиэлементом C.

    Учитывая, что p6=p7, то получим следующую формулу:

    PC=p6*p7= p62 (3)

    4. Элементы 8, 9 образуют последовательное соединение, которое заменяем соответственно квазиэлементом D.

    Учитывая, что p8=p9, то получим следующую формулу:

    PD=p8*p9= p82 (4)

    5. Элементы 10 и 11 образуют последовательное соединение, которое заменяем соответственно квазиэлементом E.

    Учитывая, что p10=p11, то получим следующую формулу:

    PE=p10*p11= p102 (5)

    6. Элементы 12 и 13 образуют последовательное соединение, которое заменяем соответственно квазиэлементом F.

    Учитывая, что p12=p13, то получим следующую формулу:

    PF=p12*p13= p122 (6)

    7. Элементы B, С, D, E образуют соединение m из n (2 из 4). Заменим их квазиэлементом G, воспользовавшись комбинаторным методом, так как что 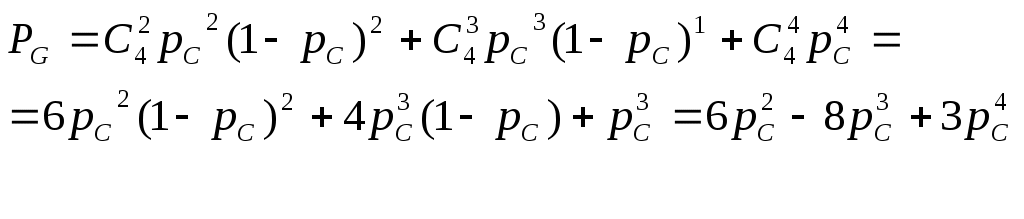, то получим:



    (7)

    8. После преобразований схема изображена на рис. 2.


    Рис. 2. Преобразованная схема

    9. В преобразованной схеме (рис. 2) элементы 1, A, G, F и 14 образуют последовательное соединение. Тогда вероятность безотказной работы всей системы:

    P=p1*pA*pG *pF*p14 (8)

    10. Так как по условию все элементы системы работают в периоде нормальной эксплуатации (постоянства интенсивности отказов (t) = = const), то вероятность безотказной работы элементов с 1 по 14 (рис. 1) подчиняются экспоненциальному закону:

    (9)

    Поток отказов при (t) = const называется простейшим и именно он реализуется в течении периода нормальной эксплуатации от окончания приработки до начала старения и износа.

    11. Результаты расчетов вероятностей безотказной работы элементов 1 – 14 исходной схемы по формуле (9) для наработки до часов представлены в таблице 2.

    12. Результаты расчетов вероятностей безотказной работы квазиэлементов A, B, C, D, E, F, G по формулам (1) - (4) и общая вероятность P также представлены в таблице 2.

    Таблица 2

    Расчет вероятности безотказной работы системы

    Элемент
    λ, %
    Наработка t, x 106 ч

    0,5
    1,0
    1,5

    1
    0,2
    0,904837418035960
    0,818730753077982
    0,740818220681718

    2,3
    0,7
    0,704688089718713
    0,496585303791410
    0,349937749111155

    4,5,6,7,8,9,10,11
    0,65
    0,722527353642072
    0,522045776761016
    0,377192353563157

    12,13
    0,7
    0,704688089718713
    0,496585303791410
    0,349937749111155

    14
    0,6
    0,740818220681718
    0,548811636094026
    0,406569659740599

    А
    -
    0,496585303791410
    0,246596963941606
    0,122456428252982

    В
    -
    0,522045776761016
    0,272531793034013
    0,142274071586514

    С
    -
    0,522045776761016
    0,272531793034013
    0,142274071586514

    D
    -
    0,522045776761016
    0,272531793034013
    0,142274071586514

    E
    -
    0,522045776761016
    0,272531793034013
    0,142274071586514

    F
    -
    0,496585303791410
    0,246596963941606
    0,122456428252982

    G
     -
    0,719818920154969
    0,300255870981851
    0,099641480347060

    P



    0,118985267222479
    0,008204108081878
    0,000450038811229




    Элемент
    λ, %
    Наработка t, x 106 ч

    2,0
    2,5
    3,0

    1
    0,2
    0,670320046035639
    0,606530659712633
    0,548811636094026

    2,3
    0,7
    0,246596963941606
    0,173773943450445
    0,122456428252982

    4,5,6,7,8,9,10,11
    0,65
    0,272531793034013
    0,196911675204194
    0,142274071586514

    12,13
    0,7
    0,246596963941606
    0,173773943450445
    0,122456428252982

    14
    0,6
    0,301194211912202
    0,223130160148430
    0,165298888221587

    А
    -
    0,060810062625218
    0,030197383422319
    0,014995576820478

    В
    -
    0,074273578214334
    0,038774207831722
    0,020241911445804

    С
    -
    0,074273578214334
    0,038774207831722
    0,020241911445804

    D
    -
    0,074273578214334
    0,038774207831722
    0,020241911445804

    E
    -
    0,074273578214334
    0,038774207831722
    0,020241911445804

    F
    -
    0,060810062625218
    0,030197383422319
    0,014995576820478

    G
     -
    0,029912804141752
    0,008561058836239
    0,002392562968852

    P



    0,000022332475061
    0,000001056518594
    0,000000048807096


    13. На рис. 3 представлен график зависимости вероятности безотказной работы системы P от времени (наработки) t.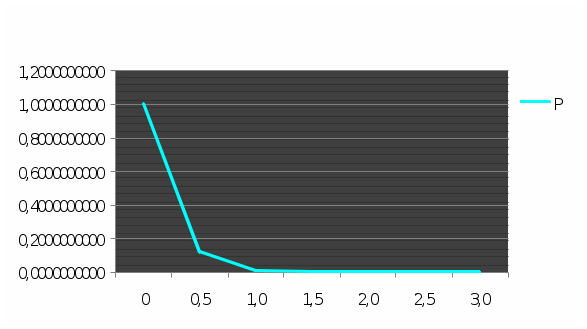



    Рис 3. Изменение вероятности безотказной работы исходной системы (Р)
    По графику (рис. 3, кривая P) находим для - процентную наработку системы ч.

    Процентная наработка - время, в течении которого отказ не наступит с вероятностью (%):

    14. Проверочный расчет при ч. показывает (таблица 3), что .

    Таблица 3

    Расчет вероятности безотказной работы системы для и

    Элемент
    λ, %
    Наработка t, x 106 ч

    0,08
    0,12

    1
    0,2
    0,984127320055285
    0,976285709757909

    2,3
    0,7
    0,945539135890396
    0,919431256095125

    4,5,6,7,8,9,10,11
    0,65
    0,949328866842890
    0,924964426543539

    12,13
    0,7
    0,945539135890396
    0,919431256095125

    14
    0,6
    0,953133787077505
    0,930530895811206

    А
    -
    0,894044257500357
    0,845353834684659

    В
    -
    0,901225297421205
    0,855559190371018

    С
    -
    0,901225297421205
    0,855559190371018

    D
    -
    0,901225297421205
    0,855559190371018

    E



    0,901225297421205
    0,855559190371018

    F
    -
    0,894044257500357
    0,845353834684659

    G



    0,996430805898300
    0,989251853111796

    P



    0,747085547586340
    0,642231578943336


    15. По условиям задания - процентную наработку системы требуется увеличить в 1,5 раза: ч. (таблица 3).

    16. Расчет показывает (таблица 3), что при ч для элементов преобразованной схемы (рис. 2) , , , , . Cледовательно, из пяти последовательно соединенных элементов минимальное значение вероятности безотказной работы имеют элементы A и F, значит являются менее надежными, поэтому именно увеличение надежности этих элементов даст максимальное увеличение надежности системы в целом.

    17. Для того, чтобы при ч система в целом имела вероятность безотказной работы , необходимо, чтобы элементы A и F имели вероятность безотказной работы (см. формулу (10)).

    (10)



    При этом значения элементов A и F останутся самым ненадежным в схеме

    (рис. 2) и рассуждения в п.16 останутся верными.

    Очевидно, значение pA = pF, полученное по формуле (10), является минимальным для выполнения условия увеличения наработки не менее, чем в 1.5 раза, при более высоких значениях увеличение надежности системы будет большим.

    18. Для определения минимально необходимой вероятности безотказной работы элементов A и F необходимо решить уравнение (8) относительно p2 при pA= pF=0,913531.

    pA= pF= p2 2

    0,913531= p2 2

    p2 =√0,913531

    p2 = 0,955788202

    19. Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону (9), то для элементов A и F при находим

    ч . (11)

    19. Таким образом, для увеличения - процентной наработки системы необходимо увеличить надежность элементов A и F и снизить интенсивность их отказов с 0,7 до ч (в 1,86 раза).

    20. Результаты расчетов для системы с увеличенной надежностью элементов 2`,3`,12`,13` приведены в таблице 4. Там же приведены расчетные значения вероятности безотказной работы элементов A` и F` и системы в целом P`. При ч вероятность безотказной работы системы , что соответствует условиям задания.

    Таблица 4

    Результаты расчетов для системы с увеличенной надежностью элемента A и F.

    Элемент
    λ, %
    Наработка t, x 106 ч

    0,5
    1,0
    1,5

    2’,3’,12’,13’
    0,376721607
    0,828315794080488
    0,686107054723190
    0,568313309857264

    A’ ,F’
    -
    0,686107054723190
    0,470742890540931
    0,322980018160919

    P’
    -
    0,227137705707351
    0,029896714352365
    0,003130675842406




    Элемент
    Наработка t, x 106 ч

    2,0
    2,5
    3,0

    2’,3’,12’,13’
    0,470742890540931
    0,389923771186155
    0,322980018160919

    A’ ,F’
    0,221598868994831
    0,152040547336033
    0,104316092131228

    P’
    0,000296565778577
    0,000026782885626
    0,000002361887668


    График приведен на рис. 4.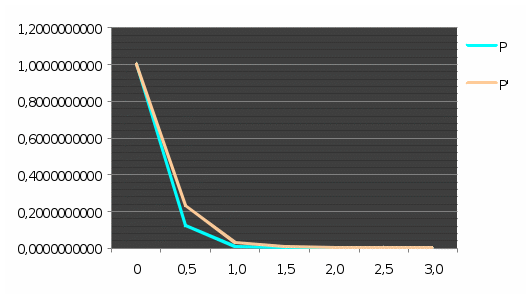



    Рис. 4. Изменение вероятности безотказной работы исходной системы (Р), системы с повышенной надежностью (Р`)
    21. Для второго способа увеличения вероятности безотказной работы системы - структурного резервирования- по тем же соображениям (см. п. 16) также выбираем элементы A и F, вероятность безотказной работы которых после резервирования должна быть не ниже (см. формулу (10)).

    22. Для повышения надежности системы добавляем к ней элементы, идентичные по надежности исходным элементам 2, 3, 12, 13, до тех пор, пока вероятность безотказной работы квазиэлементов A и F не достигнет заданного значения.

    1. Добавляем элемент 15, так как элементы 2 и 3 были соединены последовательно, а 15 элемент мы присоединяем параллельно, то формула выглядит следующим образом :

    pA = p2 (1-(1- p2)2

    0,913531=0,9194*(1-(1-0,9194)2 )

    0,913531<0,913509

    2. Добавляем элемент 16.

    0,913531=0,9194*(1-(1-0,9194)3 )

    0,913531>0,918950

    Аналогично добавляем 17, 18 для квазиэлемента F.

    23. Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рис. 2 систему достроить элементами 15, 16, 17,18 до системы (рис. 5).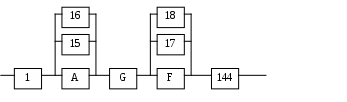




    Рис. 5. Структурная схема системы после структурного резервирования
    24. Результаты расчетов вероятностей безотказной работы системы «15`- 18`», системы в целом P`` представлены в таблице 5.

    Таблица 5.

    Результаты расчетов вероятностей безотказной работы системы «15``- 18``» системы в целом P``

    Элемент
    λ, %
    Наработка t, x 106 ч

    0,5
    1,0
    1,5

    15''-18''
    0,7
    0,704688089718713
    0,496585303791410
    0,349937749111155

    A",F"
    -
    0,686539627982369
    0,433231669691092
    0,253808480978303

    P''
    -
    0,227424205227237
    0,106500784815619
    0,018735183729868




    Элемент
    λ, %
    Наработка t, x 106 ч

    2,0
    2,5
    3,0

    15''-18''
    0,7
    0,246596963941606
    0,173773943450445
    0,122456428252982

    A",F"
    -
    0,141141321130704
    0,075761477034966
    0,039702683454525

    P''
    -
    0,002830046118667
    0,000393394853298
    0,000052132259530



    25. Расчеты показывают, что при 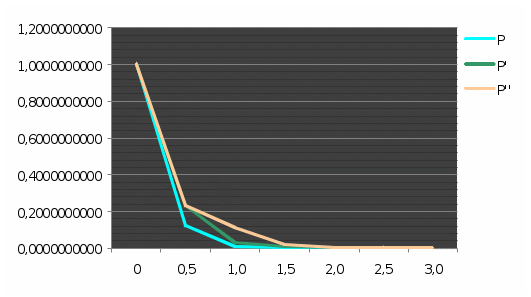ч. , что соответствует условию задания. График приведен на рис. 6.



    Рис. 6. Изменение вероятности безотказной работы исходной системы (Р), системы с повышенной надежностью (Р`) и системы со структурным резервированием элементов (Р``).
    Выводы:

    1. На графике (рис. 3, кривая P) представлена зависимость вероятности безотказной работы системы (кривая Р). Из графика видно, что 75% - наработка исходной системы составляет ч.

    2. Для повышения надежности и увеличения 75% - наработки системы в 1.5 раза (до часов) предложены два способа

    а) повышение надежности элементов A и F и уменьшение их отказов с 0,7 до ч (в 1,86 раза).

    б) нагруженное резервирование основного элемента 2,3 и 12,13 идентичными по надежности резервными элементами 15,16 и 17,18.

    3. Анализ зависимостей вероятности безотказной работы системы от времени (наработки) (рис. 6.) показывает, что второй способ повышения надежности системы (структурное резервирование) предпочтительнее первого, так как в период наработки до часов вероятность безотказной работы системы при структурном резервировании (кривая ) выше, чем при увеличении надежности элементов (кривая ).

    написать администратору сайта