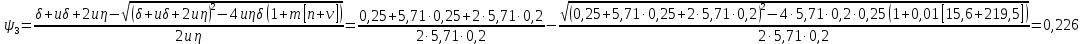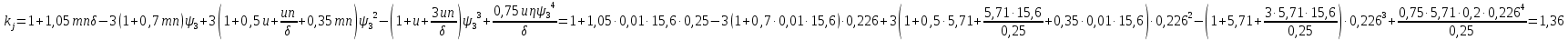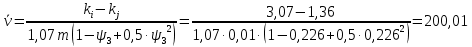Расчет параболического гиперболоида. Леонов В. А. ПС-81з. ФС-4931. Гиперболопараболо. Расчет несущей способности пространственного покрытия в форме гиперболического параболоида
 Скачать 33.03 Kb. Скачать 33.03 Kb.
|
|
Шифр ФС-4931 Леонов В. А. Расчет несущей способности пространственного покрытия в форме гиперболического параболоидаИсходные данные:
Параметры |

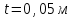

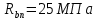


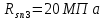
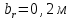


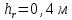
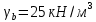

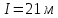
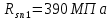

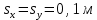

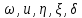
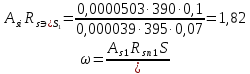
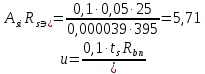
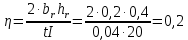
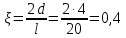

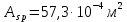
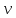 :
: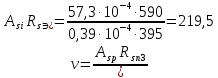
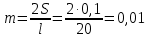
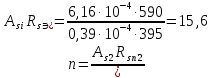
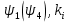
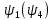 , характеризующий положение нейтральной оси линии излома и расчетный коэффициент
, характеризующий положение нейтральной оси линии излома и расчетный коэффициент 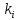 .
.
 — нейтральная ось линии излома не пересекает ребер, а
— нейтральная ось линии излома не пересекает ребер, а 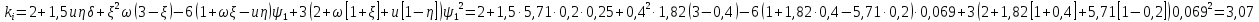

 ):
):
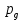 ):
):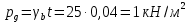
 ):
):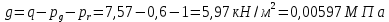
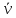 .
.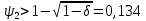
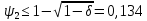
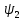 :
:
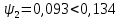
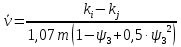
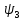 и
и 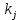 для случая, когда нейтральная ось пересекает ребро вычисляем по формулам:
для случая, когда нейтральная ось пересекает ребро вычисляем по формулам: