Железобетонные конструкции. жбк-1 климов. Расчет несущих конструкций многоэтажного гражданского здания
 Скачать 2.32 Mb. Скачать 2.32 Mb.
|
|
Нагрузки
Для расчета многопролетной плиты выделяем полосу 100 см. Нагрузка с учетом коэффициента надежности γп= 0,95 нагрузка на 1 м равна 18610∙0,95 = 17680 кН. 7.2.2 Изгибающие моменты. Определяем как для многопролетной плиты с учетом перераспределения моментов. в средних пролетах и на средних опорах 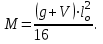 7.1) 7.1)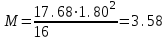 кН∙м = 3580 Н∙м. кН∙м = 3580 Н∙м.В первом пролете и на первой опоре 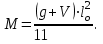 (7.2) (7.2)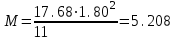 кН∙м = 5208 н∙м. кН∙м = 5208 н∙м.Так как средние плиты окаймлены по всему контуру монолитно связанными с ними балками, и под влиянием возникающих распоров изгибающие моменты умножаются на 20%, если  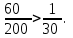 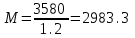 Н∙м. Н∙м.7.2.3 Подбор сечений продольной арматуры в средних пролетах и на средних опорах h0 = h - а = 6 - 1,5 = 4,5 см 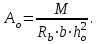 (7.3) (7.3)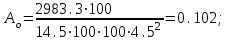 η = 0,946. η = 0,946.Принимаем сетку из 10Ø4 Вр-I с поперечной рабочей арматурой по приложению VII [5] As= 1,96 см2 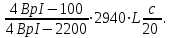 (7.4) (7.4)В первом пролете и на первой опоре ho = 4,4 см 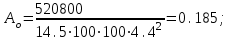 η = 0.899. η = 0.899. см2. см2.Принимается так же сетка. Над второстепенными балками устанавливаются дополнительные сетки из Ø4 Bp-I, As=3,92 см2, на расстоянии 500 мм от второстепенной балки в обе стороны. 7.3 Многопролетная второстепенная балка 7.3.1 Расчетный пролет и нагрузки. Расчетный пролет равен расстоянию в свету между главными балками lо = 6 - 0,3 = 5,7 м, средние пролеты  (7.5) (7.5)где l1 - пролет балки а - привязка разбивочной оси и внутренней грани стены, равна 0; В — длина опорного конца балки на стене равна 0,25 м.  м. м.Погонную нагрузку на балку принимаем на ширину грузовой площади, равную расстоянию между осями второстепенных балок. Таблица 7.2. Нагрузки
7.3.2 Расчетные усилия Изгибающие моменты определяем как многопролетной балки, с учетом перераспределения усилий. В первом пролете: 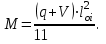 (7.6) (7.6) кН∙м. кН∙м.На первой промежуточной опоре  (7.7) (7.7)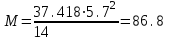 кН∙м. кН∙м.В средних пролетах и на средних опорах 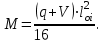 (7.8) (7.8) кН∙м. кН∙м.отрицательные моменты в средних пролетах определяется по огибающей эпюре моментов, они зависят от отношения временной нагрузки и постоянной V/q. В расчетном сечении в месте обрыва подопорной арматуры отрицательный момент при V/q=0,85<3 принимаем 40% момента на первой промежуточной опоре. Тогда отрицательный момент в среднем пролете М = 0,4∙75,98 = 30,39 кН∙м. Поперечные силы: на крайней опоре Q= 0,4∙(q + V)∙loi = 0,4∙37,418∙5,825 = 87,2 кН на первой промежуточной опоре слева Q = 0,5∙(q + V)∙l = 0,5∙37,418∙5,7 = 106,6 кН/ И на всех остальных опорах. 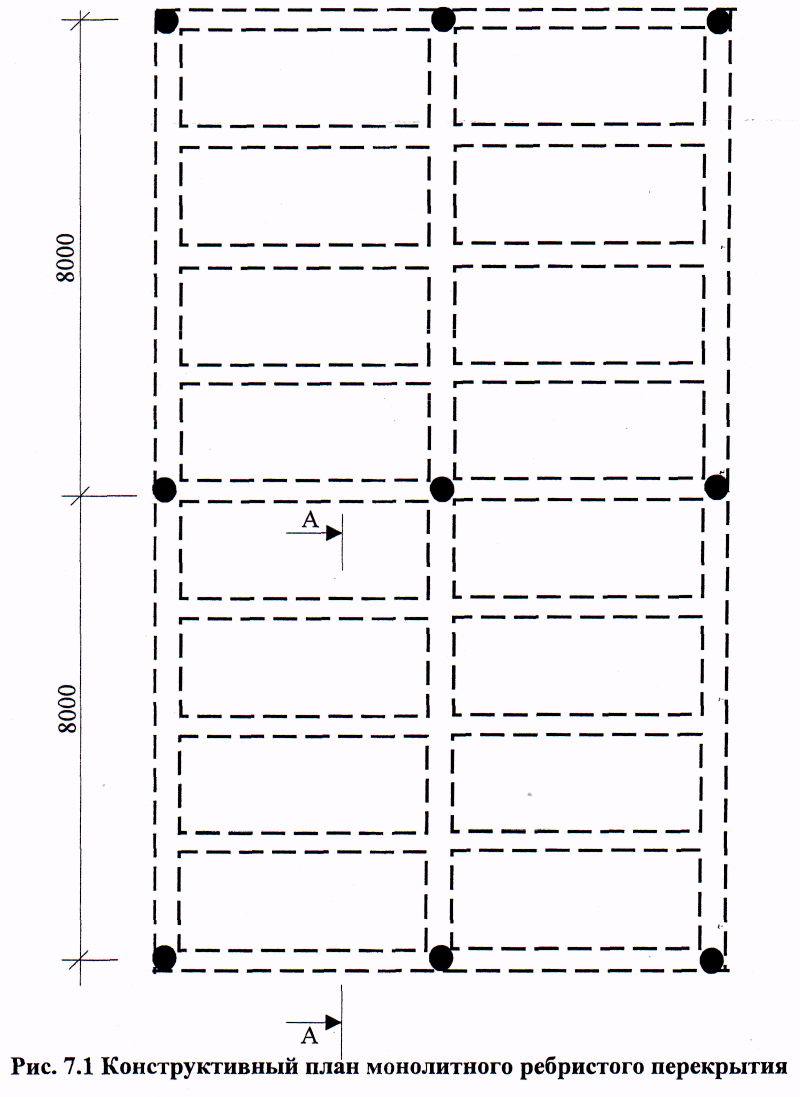 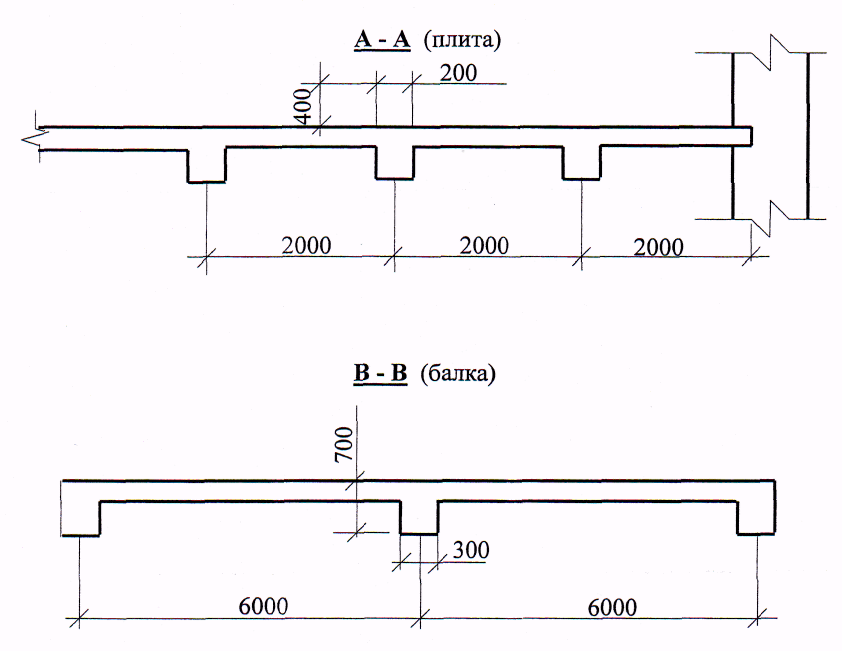 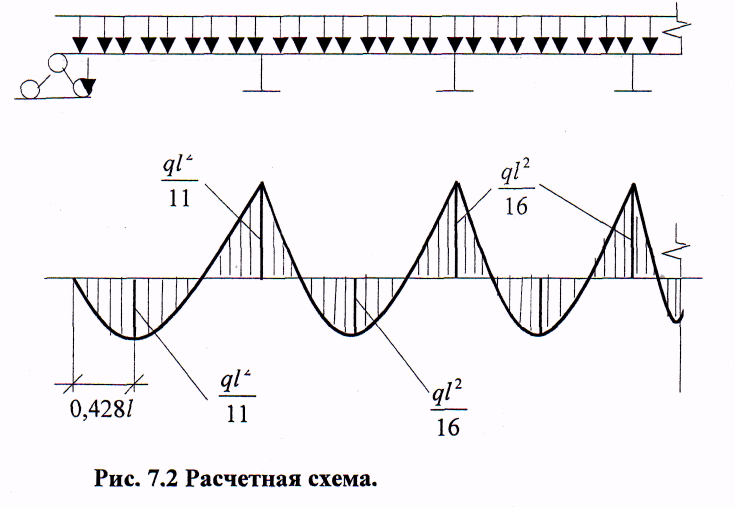 7.3.3 Определение высоты сечения балки. Высоту сечения подбираем по опорному моменту при ξ = 0,35 поскольку на опоре моменты определяются с учетом образования пластического шарнира. По табл. III. 1. [5] А0= 0,289. На опоре момент отрицательный - полка ребра в растянутой зоне. Сечение работает как прямоугольное с шириной ребра b = 20 см. 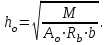 (7.9) (7.9)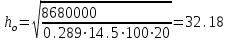 см. см.h = h0 + a= 32,18 + 3,5 = 35,68 см (7.10) П 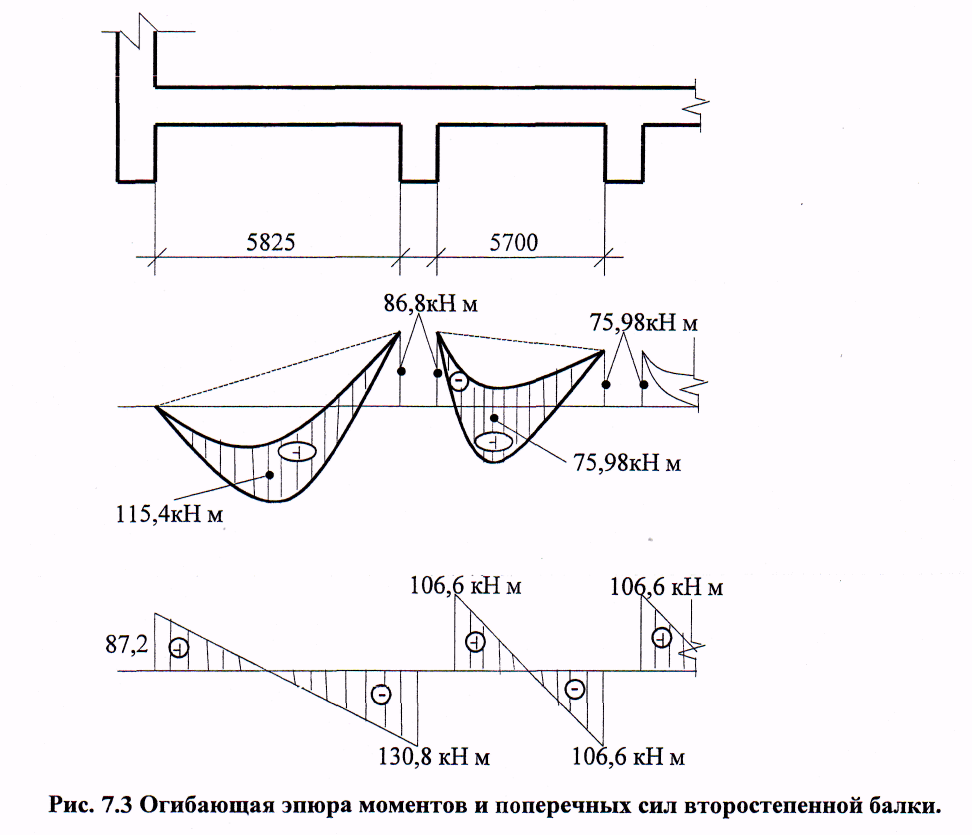 ринимаем h = 40 см, b= 20 см. в пролетах сечение тавровое - полка в сжатой зоне. Расчетная ширина полки ринимаем h = 40 см, b= 20 см. в пролетах сечение тавровое - полка в сжатой зоне. Расчетная ширина полки 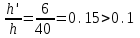 , равна , равна 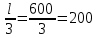 см. см.7.3.4 Расчет прочности по сечениям нормальным к продольной оси. Сечение в первом пролете: 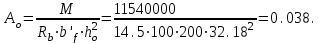 ξ = 0,04 x = ξ∙ho. (7.12) х = 0,04∙32,18 = 1,29 см < 6 см - нейтральная ось проходит в сжатой полке η = 0,98. 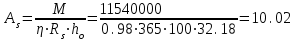 cм2 (7.13) cм2 (7.13)Принимаем 2Ø28 АIII As = 12,32 см2.  см2. см2.Принимаем 2Ø22 A III As= 7,6 см2 На отрицательный момент сечение работает как прямоугольное: 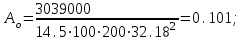 η = 0,947; η = 0,947; Принимаем 2Ø14 A III As = 3,08 см2 На промежуточной опоре.  η = 0,96. η = 0,96.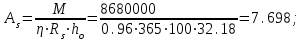 Принимаем 6Ø14 A III As = 9.54 см2. Две гнутые сетки по 3Ø14 А-Ш в каждой As = 3,08 см2 . Сечение на средней опорах: Определяется аналогично. Принимаем 6Ø7 А-Ш As = 2,31 см2. 7.3.5 Расчет прочности по сечениям наклонным к продольной оси. Выполняется для подбора поперечной арматуры. Условие постановки поперечной растянутой арматуры: Q < 0,6∙Rbb∙h0 (7.14) 130800 Н < 0,6∙14,5∙20∙32,18 = 559922 Н. Поперечная арматура устанавливается конструктивно из условия сварки Ø4 Вр I с шагом на опорах на расстоянии (1/4)∙l = 1500 мм , 0.5∙h = 100 мм, в пролете — h = 300 мм. 8. Расчет кирпичного столба первого этажа. Внутренний кирпичный столб с сетчатым армированием рассчитывается на центральное сжатие. Определение расчетных нагрузок на внутренний столб первого этажа производится по его грузовой площади. Агр=l1 ∙l2= 6 - 8 = 48 м2 (8.1) l1, l2 - шаг столбов Необходимые размеры сечения сетчатого армирования столба определяем по формуле: N < mq∙φ∙Rsk∙A (8.2) где N - расчетная продольная сила; mq - коэффициент, учитывающий влияние длительной нагрузки, mq = 1 при центральном сжатии отсутствует эксцентриситет приложения силы; φ - коэффициент продольного изгиба табл. 21.4 [6] где приведенная гибкость λm= 9, φ = 0,9 Rsk - расчетное сопротивление армированной кладки осевому сжатию;  (8.3) (8.3)R1 - расчетное сопротивление неармированной кладки осевому сжатию; μ - коэффициент принимаемый по табл.20[7]. 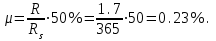 (8.4) (8.4)Rsk = 1,7 + 2∙0,23∙365 = 196,6 МПа N = [Nпокр + (nэт - 1)∙Nпер]∙1,05 (8,5) С учетом собственного веса столба N = [256,9 + (7 - 1)∙(186,7 + 754,1)]∙1,05 = 6197,0 кН Из формулы (8.2) имеем: 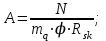 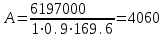 см2. см2.Размер сечения столба b = 2,5 кирпича 645x645 мм и А = 4160,2 см2. Для армирования принимаем сварные сетки:  (8.7) (8.7)где l - размер ячеек сетки S- шаг сеток - через 5 рядов.  см2. см2.Принимаем сетку Ø5 Вр-I с шагом 70 мм с рабочей арматурой в обоих направлениях. 9. Литература 1. Железобетонные и каменные конструкции. Задание на курсовой проект №1 с методическими указаниями для студентов V курса специальности пгс. СНиП 2.03.01 - 84 Бетонные и железобетонные конструкции. Нормы проектирования - М.: Стройиздат, 1985. Мандриков А.П. Примеры расчета железобетонных конструкций -М. : Стройиздат, 1979. 4- Сперанский И.Н. Сташевская С.Г. Бондаренко С.В. Примеры расчета железобетонных конструкций. Учебное пособие для вузов. - М.: Высшая школа, 1989. Банков В.Н. Сигалов Э.Е. Железобетонные конструкции. Общий курс. - М.: Стройиздат, 1985. СНиП 2.01.07 - 85. Нагрузки и воздействия. Нормы проектирования. - М.: Стройиздат, 1976. СНиП II - 22 - 81. Каменные и армокаменные конструкции - М.: Стройиздат, 1983. Руководство по проектированию каменных и армокаменных конструкций. - М.: Стройиздат, 1974. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
