РГР ПАХТ. РГР_ПАХиМП_Пример расчета_27сент.2022_Шубина_для Образ.портала (. Расчет оборудования участка подогрева исходной смеси реакторной установки
 Скачать 2.03 Mb. Скачать 2.03 Mb.
|
1 2 2.5 Определение коэффициента теплоотдачи от водяного пара к стенке с применением критериев подобия При вычислении критерия Нуссельта для движения водяного пара, согласно источнику [3, табл. 4.1, с.151], нужно воспользоваться одной из формул (4.29) – (4.35), используемых для расчета при обтекании пучка гладких труб [3, с.156]. В межтрубном пространстве водяной пар движется ламинарно (Re1 = 918), поэтому воспользуемся формулой (4.29): 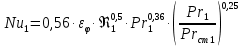 (17) (17)где 𝜀𝜑 – коэффициент, учитывающий влияние угла атаки пучка труб водяными парами [3, табл. 4.5, с.157]. Примем угол атаки 𝜑 = 30°, тогда 𝜀𝜑=0,67. При движении газов пристенный слой практически не влияет на теплообмен, поэтому 𝑃𝑟1 ⁄ 𝑃𝑟ст1 = 1. Коэффициент Прандтля для водяного пара рассчитывается по формуле: 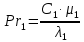 (18) (18)где 𝐶1 – истинная изобарная теплоёмкость водяного пара при 𝑡1=150°С и 𝑃1 = 0,48 МПа, Дж/(кг ∙ К), [4, табл. II-IV, с.171]; 𝜆1 – коэффициент теплопроводности водяного пара при 𝑡1=150°С и 𝑃1 = 0,48 МПа, Вт/(м ∙ К), [4, табл. II-VI, с.193]. Методом линейной интерполяции (по ссылке http://www.xn--m1abbbfjh0bzc.xn--p1ai/interpolation/inter.php) рассчитали 𝐶1 = 4193,5 Дж/(кг ∙ К) и 𝜆1 = 649,06 ∙ 10−3 Вт/(м ∙ К). Тогда 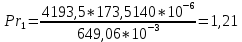 Тогда критерий Нуссельта для водяного пара: 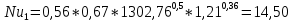 Тогда коэффициент теплоотдачи от водяного пара к стенке: 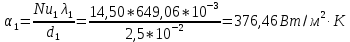 (19) (19)2.6 Определение коэффициента теплопередачи и плотности теплового потока через стенку Коэффициент теплопередачи находится по формуле: 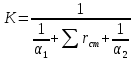 (20) (20)где 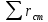 – суммарное сопротивление стенки вместе с отложениями, м2·К/Вт. – суммарное сопротивление стенки вместе с отложениями, м2·К/Вт.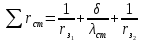 (21) (21)где 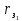 – сопротивление загрязнений со стороны водяного пара, Вт/(м∙К) – сопротивление загрязнений со стороны водяного пара, Вт/(м∙К) (Приложение 6) [3, табл. XXXI, с.531]; 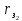 – сопротивление загрязнений со стороны бинарной смеси, Вт/(м ∙К) – сопротивление загрязнений со стороны бинарной смеси, Вт/(м ∙К) (Приложение 6) [3, табл. XXXI, с.531]; 𝛿 – толщина стенки трубы (2 мм для всех вариантов), м; 𝜆ст – коэффициент теплопроводности материала стенки, Вт/(м∙К) (Приложение 7) [3, табл. XXVIII, с.529]. Примем, что теплообменник выполнен из нержавеющей стали. Справочные данные для вычисления коэффициента теплопередачи приведены в таблице 2.1. Таблица 2.1 – Справочные данные для вычисления коэффициента теплопередачи
Используя данные таблицы 2.1, рассчитаем сопротивление стенки с отложениями: 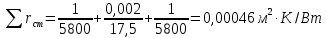 Тогда коэффициент теплопередачи: 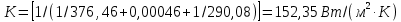 Плотность теплового потока через стенку определяем по формуле: 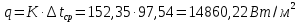 (22) (22)Вычислим температуру стенки 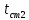 : :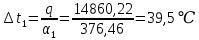 (23) (23)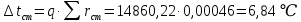 (24) (24)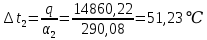 (25) (25)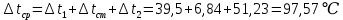 Новое расчетное значение ∆𝑡ср крайне незначительно отличается от рассчитанного ранее, поэтому температура стенки составит: 𝑡ст2 = 𝑡2 + ∆𝑡2 = 49,5 + 51,23 = 100,73 °С Температура стенки не сошлась, поэтому примем новую температуру 𝑡ст2 = 75 °С, значение которой занимает промежуточное положение между прежней и полученной. Пересчитаем μст2 при температуре tст2 = 75 °С (соответствующие значения вязкости компонентов бинарной смеси также рассчитаны методом линейной интерполяции по ссылке http://www.xn--m1abbbfjh0bzc.xn--p1ai/interpolation/inter.php): 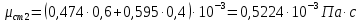 Тогда 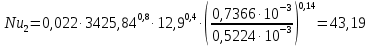 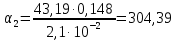 Коэффициент теплопередачи: 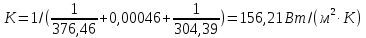 Плотность теплового потока через стенку: 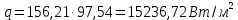 2.7 Определение количества теплообменников для подогрева смеси Площадь поверхности теплопередачи: 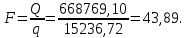 (26) (26)Площадь одного теплообменника с диаметром кожуха 400 мм и длиной труб l=4 м: 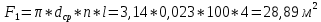 (27) (27)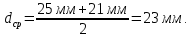 Тогда запас поверхности при установке двух теплообменников составит: 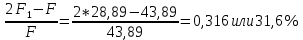 Запас для нормальной работы системы достаточный, т.к. находится в пределах 25 – 50%. Следовательно, в результате расчетов для установки рекомендуется 2 теплообменника с диаметром кожуха 𝐷 = 400 мм, с трубами длиной 4 м, числом труб 𝑛 = 100, 𝐹ор = 29 м2, 𝑆2 = 1,7∙10−2 м2, 𝑆1 = 2,5 ∙ 10−2 м2. РАСЧЕТ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ В ТРУБОПРОВОДЕ И ВЫБОР ЦЕНТРОБЕЖНОГО НАСОСА 3.1 Теоретическое обоснование расчета 3.1.1 Анализ основных уравнений для расчета Расчет гидравлических сопротивлений при движении реальных жидкостей по трубопроводам является одним из прикладных вопросов гидродинамики. Важность определения потери напора (давления) связана с необходимостью расчета затрат энергии, требуемых для компенсации этих потерь и перемещения жидкости с помощью насосов, компрессоров и т.д. Потери напора в трубопроводе в общем случае обуславливаются сопротивлением трения и местными сопротивлениями. Сопротивление трения существует при движении реальной жидкости по всей длине трубопровода. На его величину оказывает влияние режим течения жидкости (ламинарный, турбулентный, степень развития турбулентности). Местные сопротивления возникают при любых изменениях скорости потока по величине или направлении. К их числу относятся: вхождение потока в трубу и выход из нее жидкости, внезапные сужения и расширения труб, отводы, колена, тройники, запорные и регулирующие устройства (краны, вентили, задвижки и другие устройства). Внутренняя задача гидродинамики, к которой относится движение жидкости внутри трубопроводов, описывается системой уравнений Навье – Стокса [1, c.55]. Но решение системы дифференциальных уравнений в частных производных представляет собой сложную математическую задачу. Для упрощения этой задачи используют теорию подобия, методы которой позволяют заменить систему уравнений Навье–Стокса обобщенным критериальным уравнением гидродинамики [1, c.83]: 𝐸𝑢 = 𝑓(𝑅𝑒, 𝐹𝑟, 𝐻𝑜, Г) (1) где Eu ‒ критерий Эйлера; Rе ‒ критерий Рейнольдса; Fr – критерий Фруда; Но ‒ критерий гомохронности; Г – геометрический симплекс. Критерий Эйлера показывает влияние перепада гидростатического давления на движение жидкости и определяется уравнением 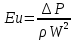 (2) (2)где ∆𝑃 ‒ перепад гидростатического давления (потери давления), Па; ρ ‒ плотность перемешиваемой жидкости, кг⁄м3; W ‒ скорость движения жидкости, м/с. Критерий Рейнольдса отражает влияние силы трения на движение жид- кости и определяется уравнением: 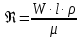 (3) (3)где l ‒ характерный линейный размер, м (для внутренней задачи гидродинамики в качестве характерного размера берут внутренний диаметр трубопровода, а в случае некруглого сечения потока – эквивалентный диаметр, т.е 𝑙 =𝑑э); μ ‒ вязкость жидкости, Па ∙ с; ρ ‒ плотность перемешиваемой жидкости, кг⁄м3; Критерий Фруда отражает влияние силы тяжести или собственного веса на движение жидкости и определяется по уравнению: 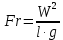 (4) (4)где 𝑔 – ускорение свободного падения, м/с2. Критерий гомохронности учитывает неустановившийся характер движения в подобных потоках и определяется уравнением: 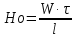 (5) (5)где τ – время, с. Геометрический симплекс (симплекс геометрического подобия) учитывает форму трубы и определяется уравнением: 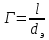 (6) (6)где l – длина трубы, м; dэ– эквивалентный диаметр трубы, м. Обычно решение обобщенного критериального уравнения представляется в виде степенной функции: 𝐸𝑢 = 𝐴 ∙ 𝑅𝑒𝑚 ∙ 𝐹𝑟𝑛 ∙ 𝐻𝑜𝑝 ∙ Г𝑞, (7) где A, m, n, p, q – эмпирические коэффициенты. В этом случае решение сводится к нахождению в литературе значений A, m, n, p, q. Сначала необходимо проанализировать обобщенное критериальное уравнение с точки зрения условия задачи: Если в задаче не оговорена нестационарность потока или это не вытекает из условий, то можно считать поток стационарным, т.е. величина показателя степени р = 0, и критерием гомохронности можно пренебречь (𝐻𝑜𝑝 = 1). В условиях вынужденного движения (с помощью насосов или компрессоров) капельной жидкости или газа влияние силы тяжести на распределение скоростей и перепад давлений в потоке очень мало и им можно пренебречь; таким образом, показатель степени n = 0 (𝐹𝑟𝑛 = 1). С принятыми допущениями уравнение (7) сводится к виду: 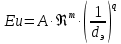 (8) (8)В результате обобщения опытных данных, полученных различными авторами, установлено, что при движении жидкости в трубопроводе с гладкими стенками в пределах 𝑅𝑒 = 4 ∙ 103 – 105 численные значения коэффициентов А = 0,158; 𝑚 = −0,25; 𝑞 = 1 [1, c.89]. Следовательно, для указанных условий уравнение (8) имеет следующий вид: 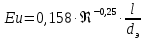 (9) (9)С учетом формулы (2) выразим величину перепада давления: 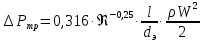 (10) (10)Величина 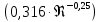 обозначается символом λ и называется коэффициентом гидравлического трения (коэффициент трения): обозначается символом λ и называется коэффициентом гидравлического трения (коэффициент трения): 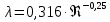 . Тогда уравнение (10) запишется в виде: . Тогда уравнение (10) запишется в виде: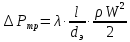 (11) (11)где λ – зависит от режима движения (величина Re) и шероховатости стенок труб. Шероховатость количественно оценивают усредненной величиной абсолютной шероховатости е и вводят понятие относительной шероховатости ε: 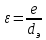 где e – абсолютная величина шероховатости стенок труб. Коэффициент гидравлического трения λ рассчитывается по общей формуле: 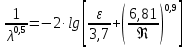 (12) (12)Для гладких труб, когда влиянием шероховатости можно пренебречь, получим: 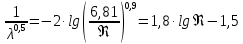 (13) (13)Для автомодельной области (по отношению к критерию Re), когда величина λ практически перестает зависеть от критерия Reи определяется лишь шероховатостью стенок труб, в уравнении (12) можно пренебречь вторым слагаемым в скобках и получить: 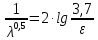 (14) (14)Если Re≤ 23 / ε, то применяется уравнение (13) для гладких труб. Если Re≥ 220 · ε-1,125, то применяется уравнение (14) для автомодельной области. Если Re принимает промежуточное значение, то применяется уравнение (12) или уравнение: 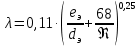 (15) (15)где 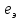 – эквивалентная абсолютная шероховатость, мм. – эквивалентная абсолютная шероховатость, мм.Приведенные уравнения (12) – (15) пригодны для изометрического потока. Для определения величины λ, кроме уравнений (12) – (15), можно использовать также график [3, с.22]. Помимо потерь на трение на линейных участках трубопровода происходят потери энергии на преодоление местных сопротивлений (повороты; внезапные расширения и сужения; запорно-регулирующая арматура и т.п.). Потери давления в местных сопротивлениях определяются по уравнению: 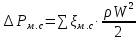 (16) (16)где 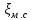 – коэффициент местного сопротивления. – коэффициент местного сопротивления.Суммарная потеря давления (напора) на преодоления трения и местных сопротивлений рассчитывается по формуле: 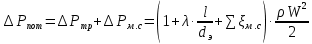 (17) (17)Если сеть представляет собой трубопровод постоянного поперечного сечения, то потери давления (напора) на полное гидравлическое сопротивление сети равны: 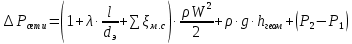 (18) (18)где 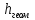 – высота подъема жидкости, м; – высота подъема жидкости, м;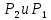 – давление соответсвенно в приемной и расходной емкостях, Па. – давление соответсвенно в приемной и расходной емкостях, Па.3.1.2 Анализ схемы установки с трубопроводом для гидравлического расчета При расчёте гидравлического сопротивления в трубопроводе от хранилища до реактора необходимо учитывать, что оно складывается из сопротивлений на трёх участках (рисунок 3.1): участок – от хранилища (1) до входа в теплообменники (12, 13); участок – движение жидкости в теплообменниках (12, 13); участок – от теплообменников (12, 13) до входа в реактор (2). Краткое описание схемы установки с трубопроводом (рисунок 3.1): трубопровод соединяет начальное 1 и конечное 2 хранилища; насос 3 установлен у хранилища 1, следовательно, трубопровод напорный; в трубопровод включено три участка общей длиной 50 м (l1 = 9 м, l2 = 10 м, l3 = 31 м); семь запорных вентилей (4, 5, 6, 7, 8, 9, 10); центробежный насос 3; измерительная диафрагма 11; два кожухотрубных теплообменника (12, 13); трубопровод имеет 10 поворотов на 90°; высота подъема бинарной смеси 21 м. 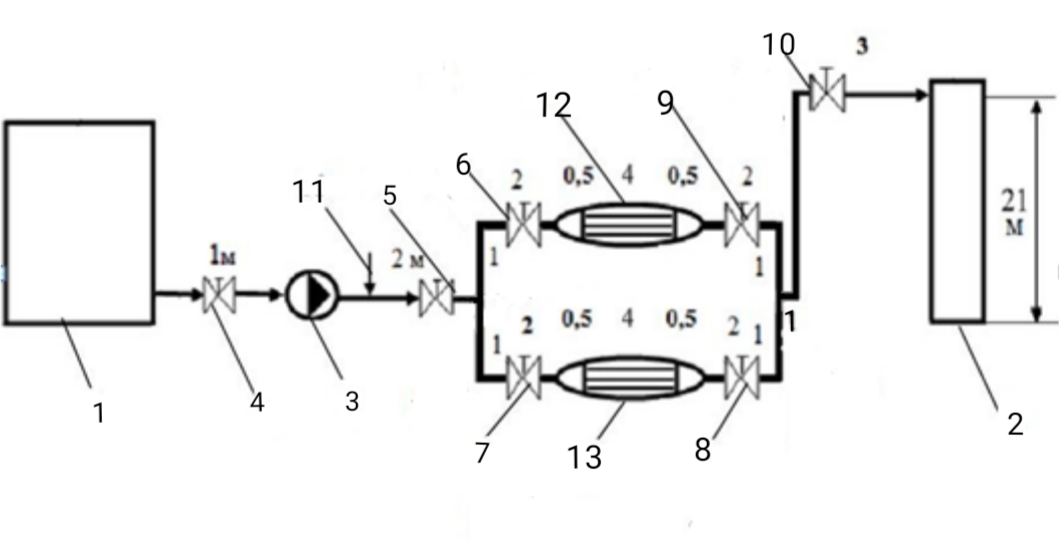 Рисунок 3.1 – Схема установки с трубопроводом для гидравлического расчета: 1 – начальное хранилище; 2 – конечное хранилище (ректификационная колонна); 3 – центробежный насос; 4, 5, 6, 7, 8, 9, 10 – запорные вентили;11 – измерительная диафрагма; 12, 13– кожухотрубные теплообменники 3.1.3 Определение характеристик смеси на разных участках трубопровода Поскольку в условиях задачи не оговариваются дополнительные изменения температуры, то принимаем поток изотермическим, т.е с сохранением температур 20°С и 79°С на соответствующих участках. Тогда на каждом участке трубопровода температуры будут следующие: 1 участок: t = 20 °С; 2 участок: t = 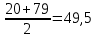 °С; °С;3 участок: t = 79 °С; На всех участках трубопровода разная температура, поэтому и разные свойства жидкости. Рассчитаем плотность и вязкость компонентов смеси, а также смеси в целом на каждом участке трубопровода с применением метода линейной интерполяции (с внесением температурной поправки к табличным данным) по ссылке http://www.xn--m1abbbfjh0bzc.xn--p1ai/interpolation/inter.php, используя справочные данные Приложений 8 и 9 [3]: Плотность этанола (Приложение 8) [3, табл. IV, с. 512]: при 20 °С: 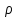 э,20 = 789 кг⁄м3; э,20 = 789 кг⁄м3;при 49,5 °С: 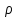 э,49,5 = 763,45кг⁄м3; э,49,5 = 763,45кг⁄м3; при 79 °С: 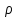 э,79 = 735,95 кг⁄м3. э,79 = 735,95 кг⁄м3.Вязкость этанола (Приложение 9) [3, табл. IX, с. 516‒517]: при 20 °С: 𝜇э,20 = 1,19 ∙ 10−3 Па ∙ с; при 49,5 °С: 𝜇э,49,5 = 0,707 ∙ 10−3 Па ∙ с; при 79 °С: 𝜇э,79 = 0,443 ∙ 10−3 Па ∙ с . Плотность уксусной кислоты (Приложение 8) [3, табл. IV, с. 512]: при 20 °С: 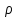 у,20 = 1048 кг⁄м3; у,20 = 1048 кг⁄м3;при 49,5 °С: 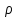 у,49,5 = 1016,08 кг⁄м3; у,49,5 = 1016,08 кг⁄м3; при 79 °С: 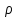 у,79 = 982,15 кг⁄м3. у,79 = 982,15 кг⁄м3.Вязкость уксусной кислоты (Приложение 9) [3, табл. IX, с. 516‒517]: при 20 °С: 𝜇у,20 = 1,22 ∙ 10−3 Па ∙ с; при 49,5 °С: 𝜇у,49,5 = 0,796 ∙ 10−3 Па ∙ с; при 79 °С: 𝜇у,79 = 0,567 ∙ 10−3 Па ∙ с . Для смеси этанол – уксусная кислота с известными долями компонентов χэ = 0,6, χу = 0,4 определим плотность и вязкость на каждом участке трубопровода. Плотность смеси: 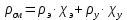 при 20 °С: 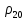 = 789 ∙ 0,6 + 1048 ∙ 0,4 = 892,6 кг⁄м3; = 789 ∙ 0,6 + 1048 ∙ 0,4 = 892,6 кг⁄м3;при 49,5 °С: 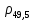 = 763,45 ∙ 0,6 + 1016,08 ∙ 0,4 = 864,502 кг⁄м3; = 763,45 ∙ 0,6 + 1016,08 ∙ 0,4 = 864,502 кг⁄м3;при 79 °С: 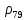 = 735,95 ∙ 0,6 + 982,15 ∙ 0,4 = 834,43 кг⁄м3. = 735,95 ∙ 0,6 + 982,15 ∙ 0,4 = 834,43 кг⁄м3.Вязкость смеси: 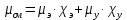 при 20 °С: 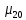 = (1,19 ∙ 0,6 + 1,22 ∙ 0,4) ∙ 10−3 = 1,202 ∙ 10−3 Па ∙ с; = (1,19 ∙ 0,6 + 1,22 ∙ 0,4) ∙ 10−3 = 1,202 ∙ 10−3 Па ∙ с;при 49,5 °С: 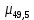 = (0,707 ∙ 0,6 + 0,796 ∙ 0,4) ∙ 10−3 = 0,7426 ∙ 10−3 Па ∙ с; = (0,707 ∙ 0,6 + 0,796 ∙ 0,4) ∙ 10−3 = 0,7426 ∙ 10−3 Па ∙ с;при 79 °С: 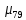 = (0,443 ∙ 0,6 + 0,567 ∙ 0,4) ∙ 10−3 = 0,4926 ∙ 10−3 Па ∙ с. = (0,443 ∙ 0,6 + 0,567 ∙ 0,4) ∙ 10−3 = 0,4926 ∙ 10−3 Па ∙ с.Для проведения дальнейших расчетов исходные данные и результаты расчетов необходимо занести в таблицу 3.1. Таблица 3.1 – Исходные данные и результаты расчета потерь напора на участках сети
Продолжение таблицы 3.1 – Исходные данные и результаты расчета потерь напора на участках сети
3.2 Перевод массового расхода жидкости в объемный В дальнейших расчетах используется объемный расход жидкости V𝑐, м3⁄с. Перевод осуществляется для каждого участка трубопровода по формуле: 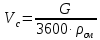 (19) (19)1 участок: 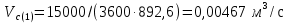 2 участок: 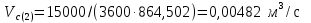 3 участок: 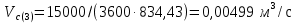 Занесем полученные результаты в таблицу 3.1. 3.3 Определение ориентировочного диаметра трубопровода По справочной таблице (таблица 3.2) выбираем скорость движения бинарной смеси в напорном трубопроводе W = 2 м/с [3, с.17]. Таблица 3.2 – Скорость движения бинарной смеси в напорном трубопроводе  Средний диаметр трубопровода для каждого участка можно определить по формуле: 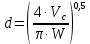 (20) (20)1 участок: 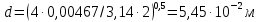 2 участок: 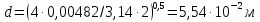 3 участок: 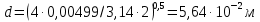 Занесем полученные результаты в таблицу 3.1 3.4 Выбор стандартного диаметра трубопровода Промышленность выпускает гостированный сортамент труб, среди кото- рых необходимо выбрать трубы с диаметром наиболее близким к расчетному (см. п. 3.3). Обозначаются трубы: dн х δ, где 𝑑н – наружный диаметр трубы, мм; δ – толщина стенки трубы, мм. При этом внутренний диаметр трубы определяется: 𝑑вн = 𝑑н – 2δ. (21) Гостированные размеры труб по ГОСТ 8732–78 составляют следующий ряд, мм: 14х2; 18х2; 25х2; 32х2,5; 38х2,5; 45х3; 57х3; 76х3,5; 89х4,5; 108х4,5; 133х4; 159х4,5; 219х6; 272х7; 325х8; 377х10; 426х11; 465х13. Согласно п. 3.3, внутренний размер трубы на 1 участке составляет 54,5 мм. Тогда наружный размер составляет: 𝑑н = 54,5 + 2 · 3 = 60,5 мм. Наиболее близкая по размерам труба по ГОСТ 76х3,5 мм. Гостированный внутренний диаметр будет равен: 𝑑внГОСТ = 𝑑нГОСТ − 2δ = 76 − 2 ∙ 3,5 = 69 мм, поэтому эквивалентный диаметр примем равным 0,069 м. Аналогично рассчитаем и выберем размеры труб для 2 и 3 участков. Для них стандартная труба имеет те же параметры 76х3,5 мм, что и для 1 участка из-за незначительного отличия 𝑑1, 𝑑2 и 𝑑3 (см. п. 3.3). Значит, эквивалентные диаметры труб будут такими же: 𝑑э = 0,069 м. 3.5 Уточнение скорости движения жидкости Выразим скорость движения жидкости на каждом участке: 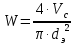 (22) (22)1 участок: 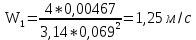 2 участок: 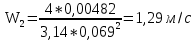 3 участок: 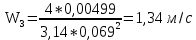 Занесем полученные результаты в таблицу 3.1 3.6 Определение режима движения жидкости Режим движения жидкости на каждом участке определим по уравнению Рейнольдса: 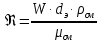 (23) (23)1 участок: 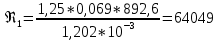 2 участок: 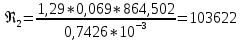 3 участок: 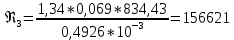 Занесем полученные результаты в таблицу 3.1 Сравним результаты расчета со справочными значениями числа Re для разных режимов течения потока [3, c.17]:  Развитые турбулентные течения характеризуются Re > 104; т.к для всех участков рассчитанные значения Re (табл. 3.1) больше 104, следовательно, режим движения бинарной смеси в трубопроводе – развитый турбулентный. 3.7 Определение коэффициента гидравлического трения Примем среднее значение шероховатости e = 0,2 мм. Тогда относительная шероховатость составит 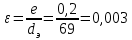 (24) (24)Для выбора формулы ля расчета коэффициента трения λ проверим условия: 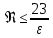 ; ; 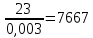 Cогласно таблице 3.1, Re 1, Re 2, Re 3 > 7667. Следовательно, условие не выполняется для всех участков трубопровода. 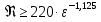 ; ; 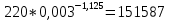 . .Cогласно таблице 3.1 Re1, Re2 < 151587, Re 3 > 151587. Следовательно, условие выполняется для третьего участка трубопровода. Следовательно, для расчета коэффициента гидравлического трения λ1 и λ2 будем использовать формулу (12): 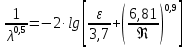 отсюда λ1 = 0,02834 λ2 = 0,02759, а для расчета λ3 – формулу (14) для автомодельной области: 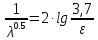 отсюда λ3 = 0,02618. Занесем полученные результаты в таблицу 3.1. 3.8 Определение коэффициентов местных сопротивлений Определим справочные значения коэффициентов местных сопротивлений согласно данным табл. 3.3 и Приложения 10 [1, c.91; 3, c.520, с.26]. Таблица 3.3 – Значения коэффициентов местных сопротивлений ξ в кожухотрубных теплообменниках
Выбраны следующие значения коэффициентов местных сопротивлений: вентиль нормальный ξвент = 4,2; вход в трубу из хранилища ξвх = 0,5; выход из трубы в аппарат ξвых = 1; измерительная диафрагма (при 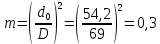 ) ξд = 18,2; ) ξд = 18,2;вход и выход из решетки теплообменника ξвх = 1,5; вход и выход из теплообменника в трубу ξвых = 1; колено ξкол = 1,1. Определим коэффициенты местных сопротивлений для каждого участка. 1 участок: ∑ 𝜉м.с (1 уч) = 𝜉вх + 4 ∙ 𝜉вент + 4 ∙ 𝜉кол + 𝜉д + 2 ∙ 𝜉вых = 0,5 + 4 ∙ 4,2 +4 ∙ 1,1 +18,2 +2 ∙ 1) = 41,9. 2 участок: ∑ 𝜉м.с (2 уч) = 2 ∙ (𝜉вх в теп + 𝜉вх в реш + 𝜉вых из теп + 𝜉вых из реш) = 2 ∙ (1,5 + 1 +1,5 + 1) = 10. 3 участок: ∑ 𝜉м.с (3 уч) = 6 ∙ 𝜉кол + 3 ∙ 𝜉вент + 𝜉вых = 6 ∙ 1,1 + 3 ∙ 4,2 + 1 = 20,2. Занесем полученные результаты в таблицу 3.1. 3.9 Определение полной потери напора в трубопроводе Сумма длин всех участков трубопровода 50 м, геометрическая высота подъема смеси hгеом = 21м, давления в приемной и расходной емкостях одинаковые 𝑃1 = 𝑃2. Тогда потери давления на участке трубопровода можно рассчитать по уравнению: 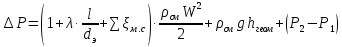 (25) (25)Потери давления на 1 участке при 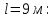 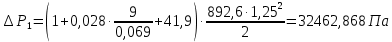 Потери давления на 2 участке при 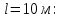 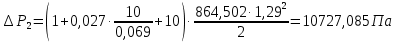 Потери давления на 3 участке при 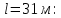 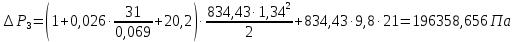 Полные потери давления в трубопроводе: 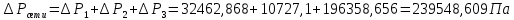 Из соотношения 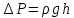 определим потери напора для каждого участка и сети в целом: определим потери напора для каждого участка и сети в целом: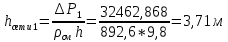 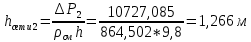 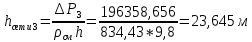  Занесем полученные результаты в таблицу 3.1. 3.10 Построение характеристики трубопроводной сети Примем, что характеристика сети представляет собой правильную параболу, выходящую из точки с координатами 𝑉𝑐 = (0; h), на которой известна расчетная точка с координатами 𝑉𝑐 = 0,00499 м3/ с = 17,964 м3/ ч и h сети = 28,621 м. Общее уравнение параболы: y=ax2 + b. Подставив значения координат расчетной точки, получим: h сети = a ∙ 𝑉𝑐2 + h геом (26) Выразим и рассчитаем коэффициент параболы: 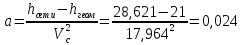 . .Тогда уравнение (26) примет вид: 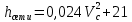 (27) (27)Примем несколько значений объемной производительности и определим для них соответствующие значения напора сети по уравнению (27). Данные внесем в таблицу 3.4 и по ним построим характеристику сети (рисунок 3.2). Таблица 3.4 –Зависимость напора сети от производительности
3.11 Выбор насоса При выборе насоса необходимо соблюдать следующие условия: напор при нулевой производительности должен быть больше, чем геометрическая высота подъема жидкости в сети; рабочая точка должна лежать в области максимального к.п.д.; рабочая точка должна лежать на нисходящей ветви графика H = f(𝑉𝑐). напор насоса (hн) должен быть больше, чем рассчитанный напор сети hн>hсети , т.е. hн>28,621 м при производительности 𝑉𝑐 = 18 м3/ ч. 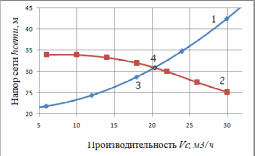 Рисунок 3.2 – Совмещение характеристик трубопроводной сети и насоса: 1 – характеристика сети; 2 – характеристика насоса; 3 – расчетная точка; 4 – рабочая точка Для выбора подходящего насоса надо воспользоваться полем характеристик насосов (Приложение 11). На этом поле отмечают необходимые для данной сети производительность и напор (Приложение 12). В данном случае наиболее близким к расчетным параметрам и подходящим насосом является насос К65‒50‒160. В марке насоса первой цифрой обозначен диаметр всасывающего патрубка, второй – диаметр нагнетательного патрубка, третьей – диаметр рабочего колеса насоса (в мм). Для того, чтобы получить характеристику выбранного насоса, необходимо в сети интернет (по ссылке: http://www.chemengrkhtu.ru/task.htm) в поле для выбора насоса внести марку насоса (в данном примере К65‒50‒160) и скопировать рисунок рабочей характеристики насоса для дальнейшей работы с ним. На рабочей характеристике насоса отмечают необходимые для данной сети производительность и напор (Приложение 13). По рабочей характеристике выбранного насоса (Приложение 13) определим параметры данного насоса: центробежный насос К65‒50‒160 производительностью 18 м3/ч и напором 30 м, диаметр рабочего колеса 162 мм, n = 2900 об/мин, КПД 60%, потребляемая мощность 3 кВт. На рисунке 3.2 построим фрагмент (рабочую часть) характеристики выбранного насоса по данным его рабочей характеристики для совмещения характеристик трубопроводной сети 1 и насоса 2. Расположение рабочей точки (4) относительно расчетной точки (3) показывает (рисунок 3.2), что насос может преодолеть гидравлические сопротивления сети и подавать в неё заданную смесь. Таким образом, к установке предлагается центробежный насос К65‒50‒160, который обеспечит перекачивание 17,964 м3/ч смеси этиловый спирт – уксусная кислота, нагретой до 79 °С, по трубопроводу из хранилища через теплообменники в ректификационную колонну. При этом производительность составит 18 м3/ч, напор 30 м, диаметр рабочего колеса 162 мм, n = 2900 об/мин, КПД 60%, потребляемая мощность 3 кВт. ЗАКЛЮЧЕНИЕ Таким образом, в результате теплового и гидравлического расчета оборудования участка подогрева исходной бинарной смеси этиловый спирт – уксусная кислота для реакторной установки с заданными параметрами процесса к установке предлагаются: два теплообменника с диаметром кожуха 𝐷 = 400 мм, с трубами длиной 4 м, числом труб 𝑛 = 100, 𝐹ор = 29 м2, 𝑆2 = 1,7 ∙ 10−2 м2, 𝑆1 = 2,5 ∙ 10−2 м2; центробежный насос К65‒50‒160, который обеспечит перекачивание 17,964 м3/ч смеси этиловый спирт – уксусная кислота, нагретой до 79 °С, по трубопроводу из хранилища через теплообменник в реакторную установку; при этом производительность насоса составит 18 м3/ч, напор 30 м, диаметр рабочего колеса 162 мм, 𝑛 = 2900 об/мин, КПД 60%, потребляемая мощность 3 кВт. БИБЛИОГРАФИЧЕСКИЙ СПИСОК Касаткин А.Г. Основные процессы и аппараты химической технологии: учебник для вузов. ‒ М.: ОООТИД «Альянс», 2004. ‒ 753 с. Студенческая библиотека онлайн: [Электронный ресурс] // Конструкция теплообменника, Виды теплообменников, Сведения о теплоносителе:https://studbooks.net/2286594/matematika_himiya_fizika/konstruktsiya_teploobmen nika. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. ‒ М.: ОООТИД «Альянс», 2006. ‒ 576 с. Ривкин С.Л., Александров А.А. Теплофизические свойства воды и водяного пара. – М.: Энергия, 1980. – 424 с., ил. ПРИЛОЖЕНИЯПриложение 1Номограмма для определения теплоемкости жидкости [3] Пересчет в СИ: 1 ккал/(кг×°С) = 4,189×103 Дж (кг×К) 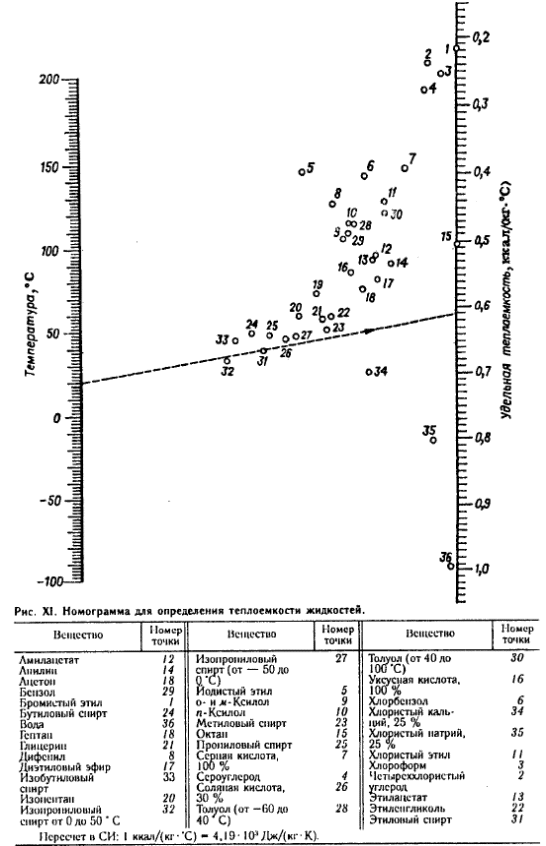 Приложение 2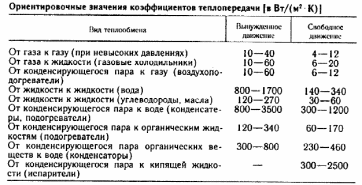 Приложение 3Основные характеристики теплообменников [3] 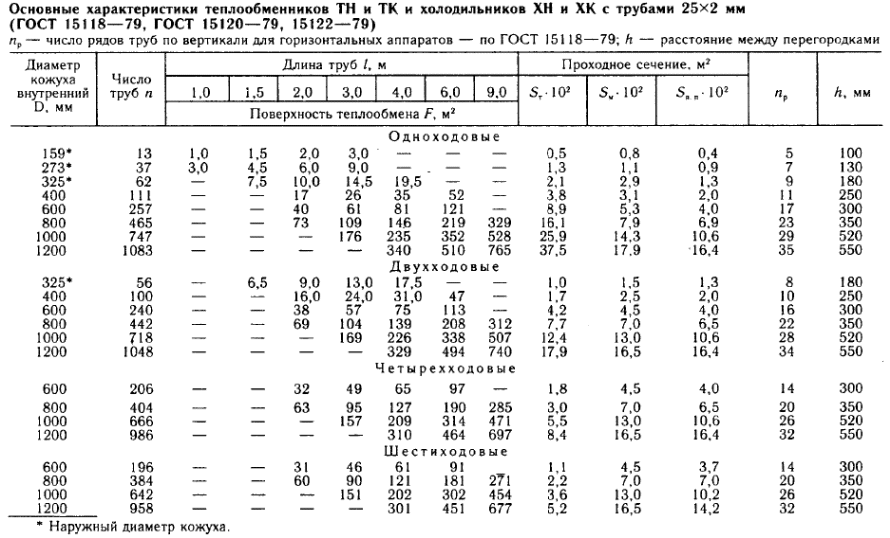 Приложение 4Коэффициент теплопроводности некоторых жидкостей [3] 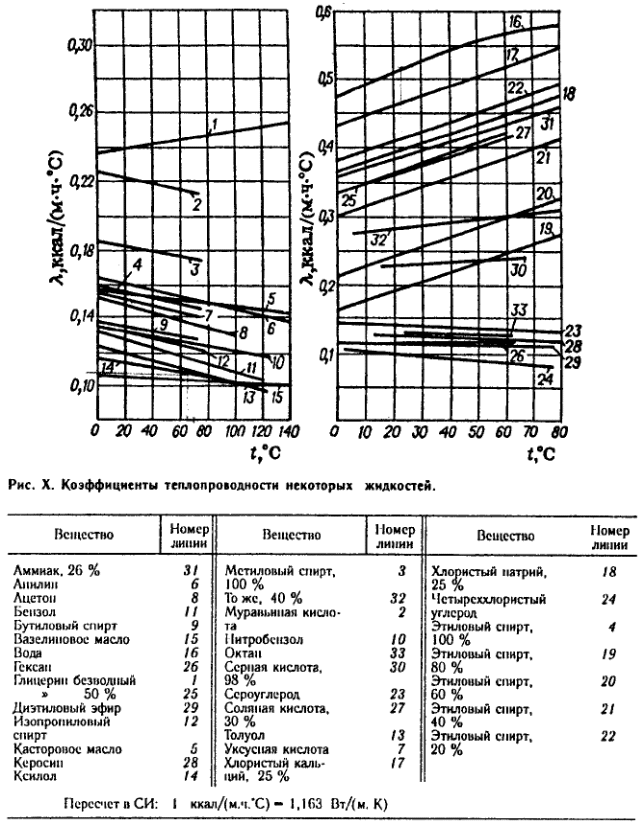 Приложение 5Коэффициент 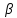 объемного расширения жидких веществ и водных растворов объемного расширения жидких веществ и водных растворов в зависимости от температуры [3] 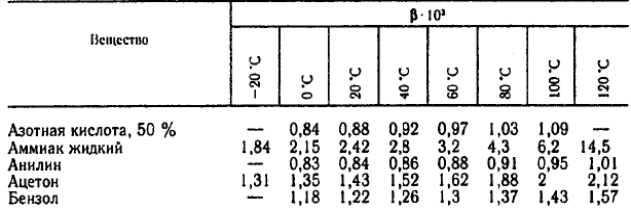 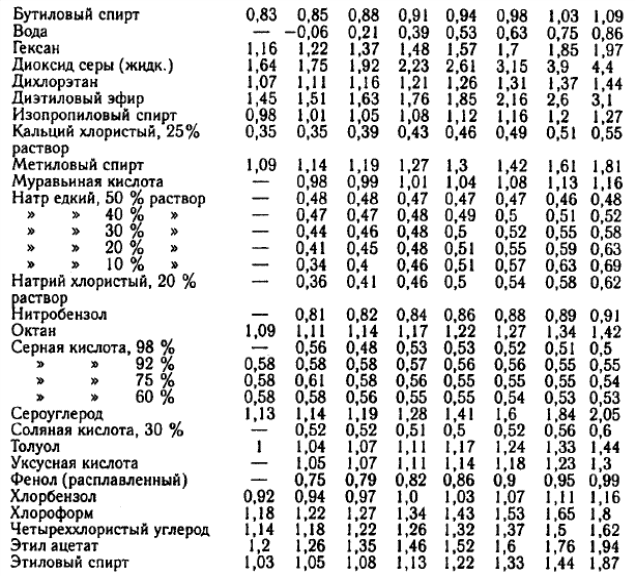 Приложение 6Среднее значение тепловой проводимости загрязнений стенок[3]  Приложение 7Коэффициенты теплопроводности некоторых материалов при 0 - 100ºС [3] 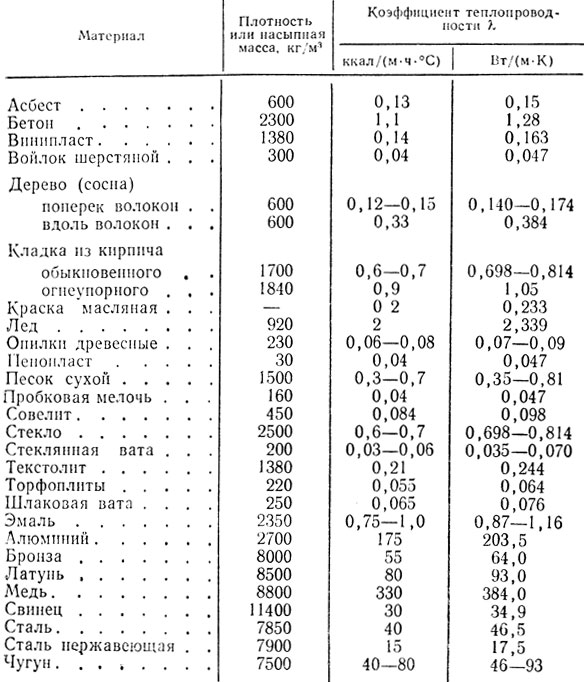 Приложение 8Плотность жидких веществ и водных растворов в зависимости от температуры [3]  Приложение 9Динамические коэффициенты вязкости жидких веществ и водных растворов в зависимости от температуры [3] 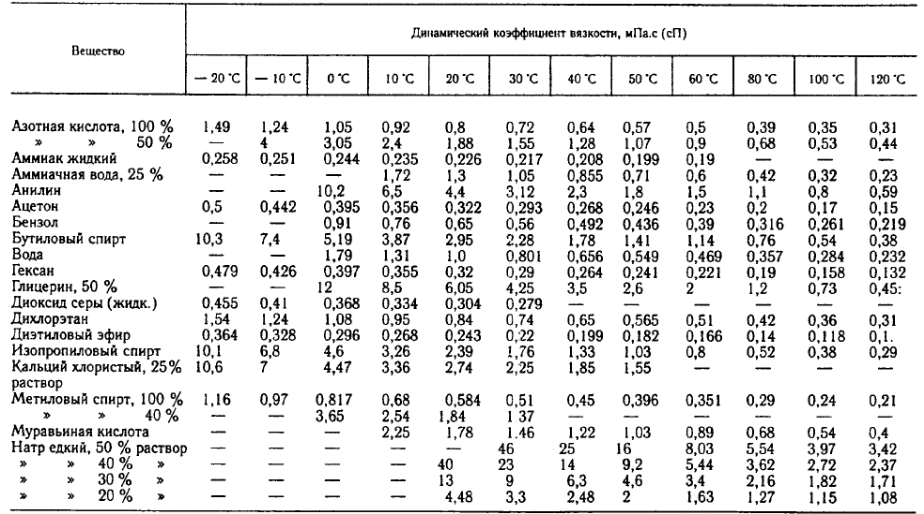 Продолжение приложения 9Динамические коэффициенты вязкости жидких веществ и водных растворов в зависимости от температуры [3] 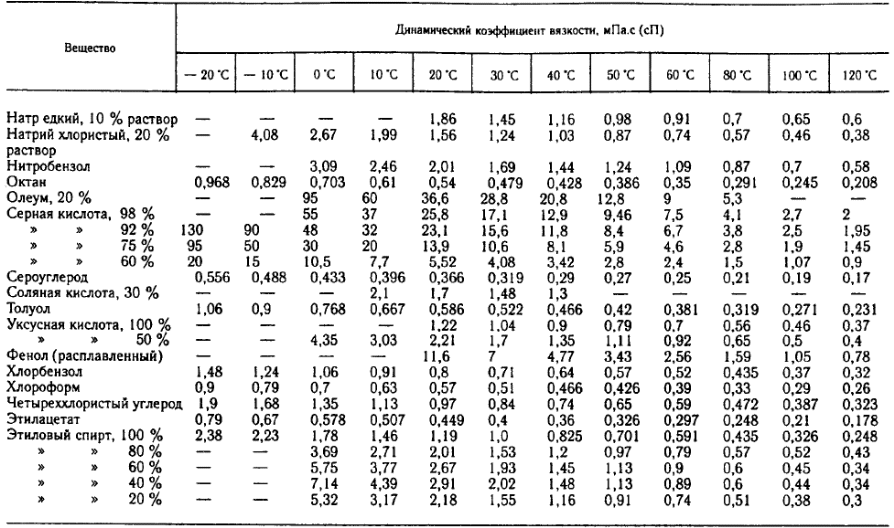 Приложение 10Коэффициенты местных сопротивлений [3] 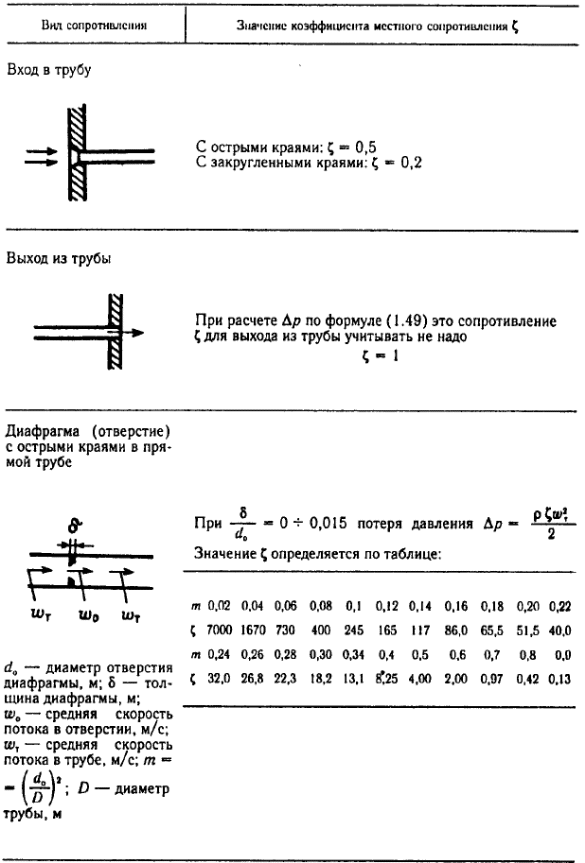 Продолжение 1 приложения 10Коэффициенты местных сопротивлений [3]  Продолжение 2 приложения 10Коэффициенты местных сопротивлений [3]  Приложение 11Поле характеристик центробежных насосов при числе оборотов n=2900 об/мин 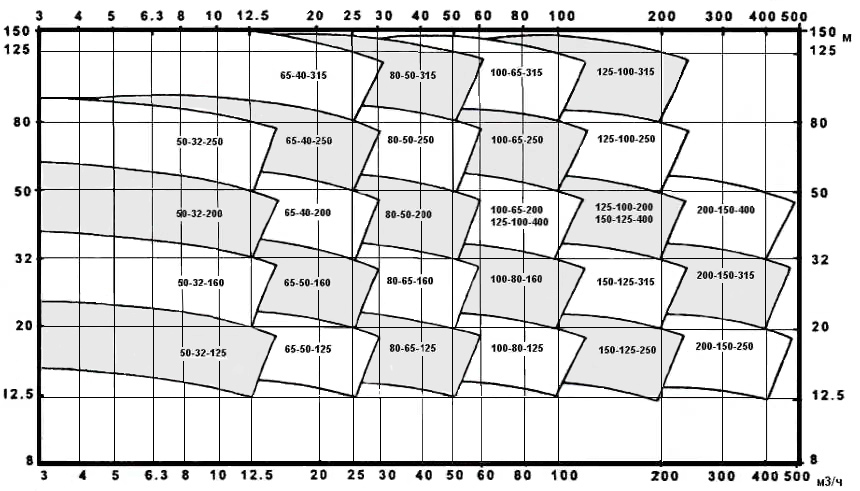 Приложение 12 Построения в поле характеристик центробежных насосов для выбора насоса по рассчитанным данным производительности и напора сети  Приложение 13 Рабочая характеристика центробежного насоса 65-50-160 при частоте n=2900 об/мин (Q или 𝑉̇ - производительность насоса, м3/ч) с построениями по рассчитанным данным производительности и напора сети 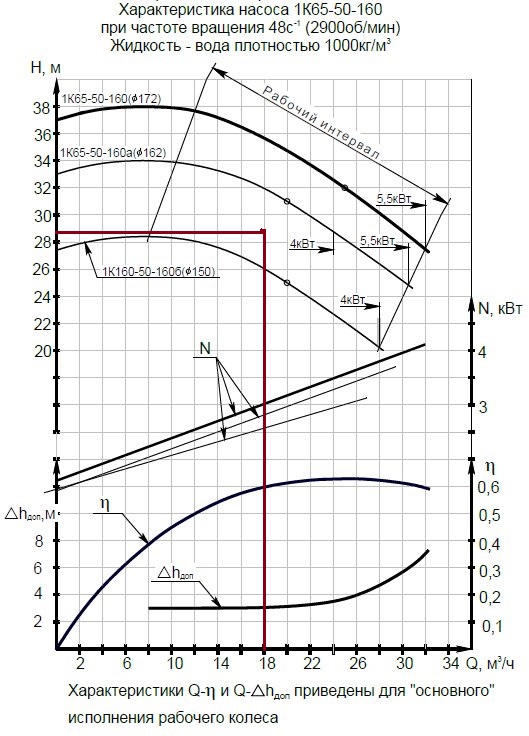 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
