КУРСОВАЯ проектирование каркасных. Расчет ограждающих и несущих конструкций теплой кровли. Разрезной прогон. Исходные данные

• Название: Расчет ограждающих и несущих конструкций теплой кровли. Разрезной прогон. Исходные данные
• Дата: 05.05.2022
• Размер: 2.61 Mb.
• Имя файла: КУРСОВАЯ проектирование каркасных.doc
• Тип: Документы; #513411
• страница: 2 из 3

2. РАСЧЕТ ГНУТОКЛЕЕНОЙ ТРЕХШАРНИРНОЙ РАМЫ

2.1. Геометрические размеры по оси рамы

Расчетный пролет рамы составляет 29,6 м;

Высота здания до конька f = 7,5 м;

Шаг конструкций 3 метра;

Уклон ригеля 1:4, т.е. угол наклона ригеля  = 1402; tg = 0,25; sin = 0,24; cos = 0,97.

Высота стойки от верха фундамента до точки пересечения касательных по осям стойки и ригеля:

.
По условиям гнутья, толщина досок после фрезеровки должна приниматься не более

1,6÷2,5см. Принимаем доски толщиной после фрезеровки . Радиус гнутой части принимаем равным:

,

Угол в карнизной гнутой части между осями ригеля стойки:



Максимальный изгибающий момент будет в среднем сечении гнутой части рамы,

которое является биссектрисой этого угла, тогда получим

;

; ;

Центральный угол гнутой части рамы в градусах и радианах будет равен:

или

;



;

; ;

Длина гнутой части:

.

Длина стойки от опоры до начала гнутой части:

.

Длина полуригеля:

.

Длина полурамы:

;

Сбор нагрузок на раму

Нагрузку от покрытия (постоянная нагрузка) принимаем по предварительно выполненным расчетам ограждающих конструкций:

нормативная ;

расчетная .

Собственный вес рамы определяем при 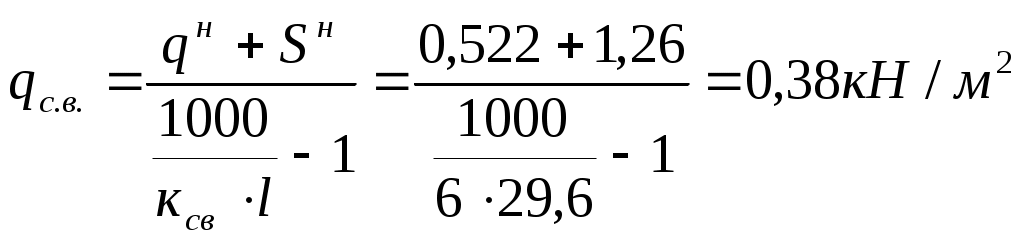из выражения

, где

– расчетный пролет рамы;

– нормативная снеговая нагрузка для III снегового района, которая определяется как произведение расчетной нагрузки по СНиП 2.01.07-85* на коэффициент равный 0,7; – коэффициент собственного веса рамы.

Значения погонных нагрузок, действующих на раму (при шаге 3 м)

Наименование нагрузки	Норматив­ная нагрузка, кН/м	Коэффици­ент перегрузки	Расчетная нагрузка, кН/м
Собственный вес покрытия	q = qн 3/сos = =0,5223/0,97=1,6		q = qр 3/сos= =0,573/0,97=1,76
Собственный вес рамы	0,383 = 1,14	1,1	1,25
Итого:	2,74		3,01
Снеговая	1,26∙3= 3,78		1,8∙3=5,4
Всего:	6,52		8,4

Статический расчет рамы

Максимальные усилия в гнутой части рамы возникают при действии равномерно распределенной нагрузки по пролету. Опорные реакции:

вертикальные: ;

горизонтальные: .

Максимальный изгибающий момент в раме возникает в центральном сечении гнутой части. Координаты этой точки определяем из следующих соотношений:

;

.

Определяем М и N в этом сечении:

;

.

Подбор сечений и проверка напряжений

В криволинейном сечении , а продольная сила .

Расчетное сопротивление сжатию и изгибу для сосны II сорта при ширине (доски шириной до фрезерования) в соответствии с табл.3 СНиП равно .

коэффициент условий работы (табл. 5 СНиП II-25-80)

коэффициент ответственности сооружения ( ), получим

.

Требуемую высоту сечения приближенно определим, преобразовав формулу проверки сечения на прочность, по величине изгибающего момента, а наличие продольной силы учтем введением коэффициента 0,6.

.

Принимаем с запасом высоту сечения из 62 слоев досок толщиной после строжки . Тогда .

Высоту сечения ригеля в коньке принимаем из условия из 20 слоев досок толщиной после строжки : .

Высоту сечения опоры рамы принимаем из условия:






Геометрические характеристики принятого сечения криволинейной части рамы:

;

;

.

В соответствии с п. 3.2 СНиП II-25-80 к расчетным сопротивлениям принимаются следующие коэффициенты условий работы:

(табл. 5);

по интерполяции согласно табл. 7;

(табл. 8);

Радиус кривизны в гнутой части по нейтральной оси будет равен:



Отношение , тогда по интерполяции значений

табл. 9[1] находим коэффициент (табл. 9, для R_c и R_и);

(табл. 9, для R_p).

Проверка напряжения при сжатии с изгибом

Изгибающий момент, действующий в биссектрисном сечении находится на расстоянии от расчётной оси , равном :

.

Расчетные сопротивления древесины сосны II сорта:

сжатию и изгибу:



растяжению:

.

Здесь 15 МПа и 9 МПа – значения соответствующих расчетных сопротивлений, принимаемые по табл. 3 СНиП II-25-80.

Радиус инерции сечения:

.

При расчетной длине полурамы , гибкость равна:

.

Для элементов переменного по высоте сечения коэффициент , учитывающий продольный изгиб, дополнительно умножаем на коэффициент , принимаемый по табл. 1 прил. 4 СНиП II-25-80.

,

где  - отношение высоты сечения опоры к максимальной высоте сечения гнутой части:

.

Коэффициент  определяем по формуле:

,

где – коэффициент, принимаемый для деревянных конструкций.

Произведение

Определяем коэффициент , учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, по формуле (30) СНиП II-25-80:

,

где − усилию в ключевом шарнире.

Изгибающий момент по деформированной схеме:

.

Для криволинейного участка при отношении 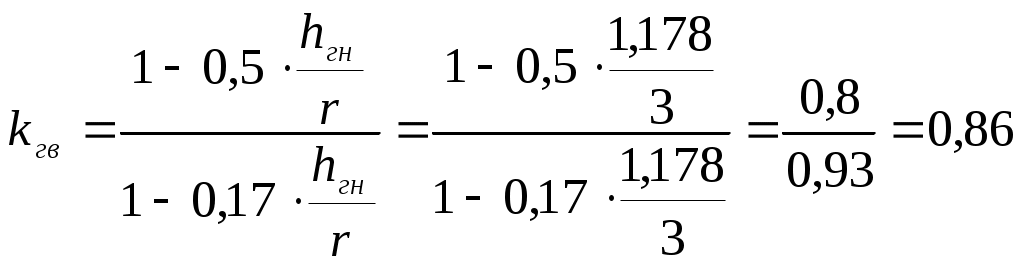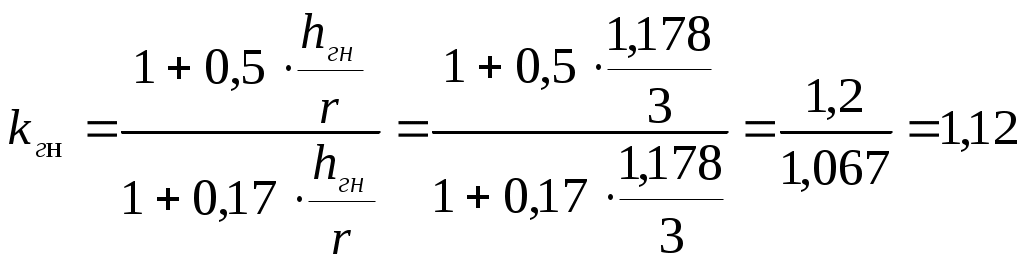согласно п.6.30 СНиП II-25-80 прочность проверяем для наружной и внутренней кромок с введением коэффициентов и к .

;

.

Расчётный момент сопротивления с учетом влияния кривизны:

для внутренней кромки:

;

для наружной кромки:

;

Напряжение по сжатой внутренней кромке определим по формуле СНиП II-25-80:

;

Условие прочности по сжатию выполняется.
;

Условие прочности по растяжению НЕ выполняется.
Добавим еще 9 слой по 1,9 см, тогда: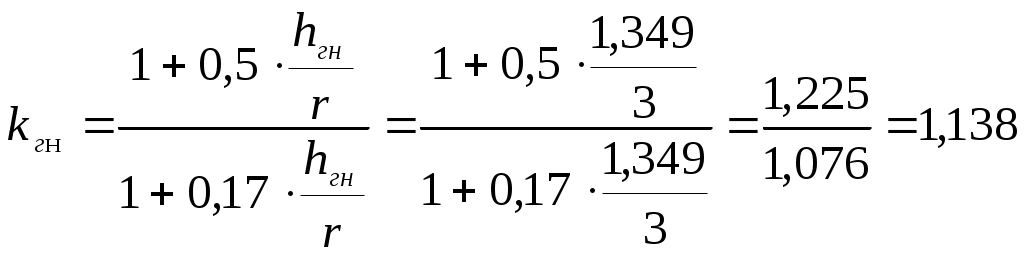

;

;

;

;



Недонапряжение составляет:

;

Условие прочности по растяжению выполняется.



Принимаем с запасом высоту сечения из 71 слоев досок толщиной после строжки . Тогда .

Высоту сечения ригеля в коньке принимаем из условия из 20 слоев досок толщиной после строжки : .

Высоту сечения опоры рамы принимаем из условия: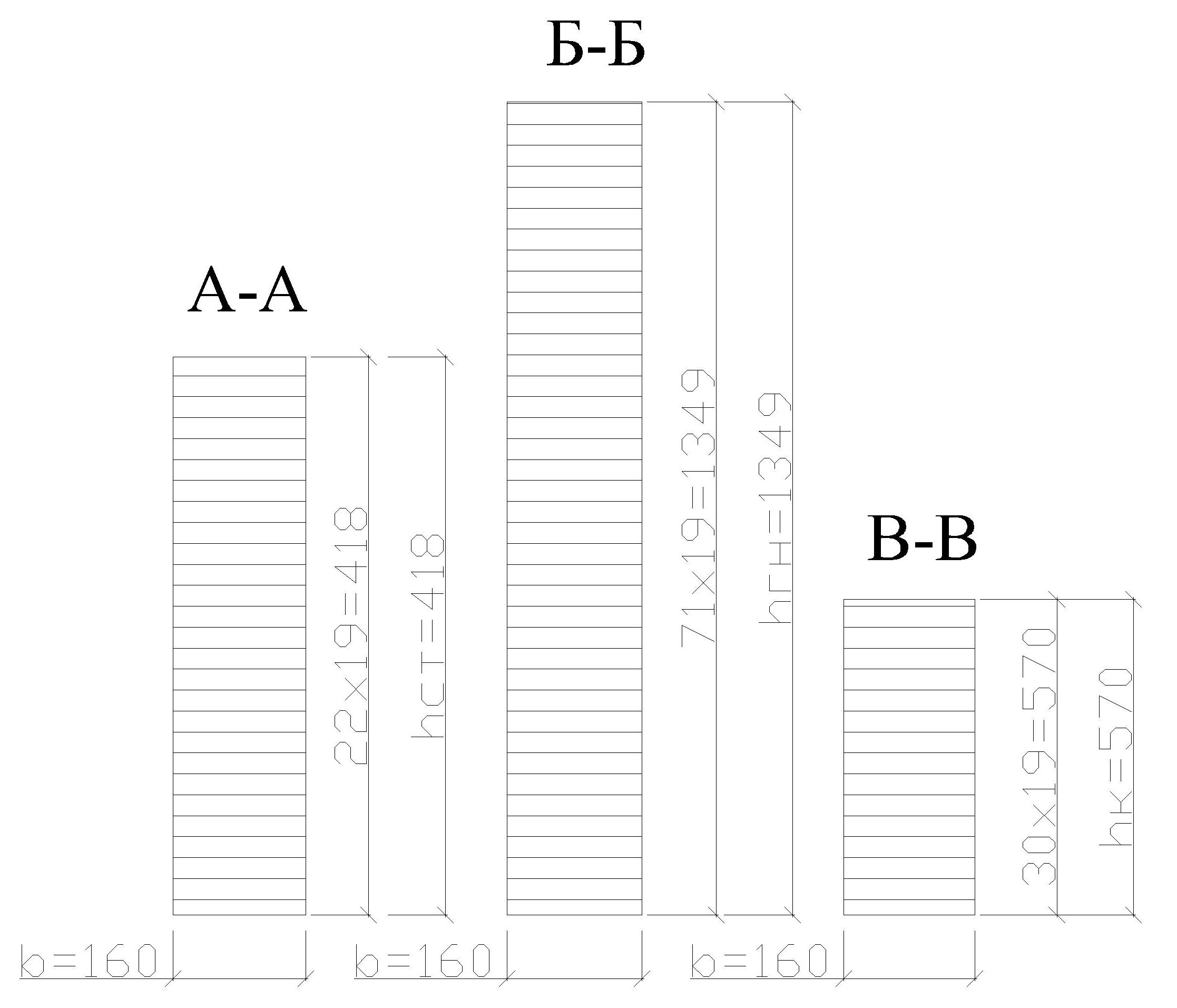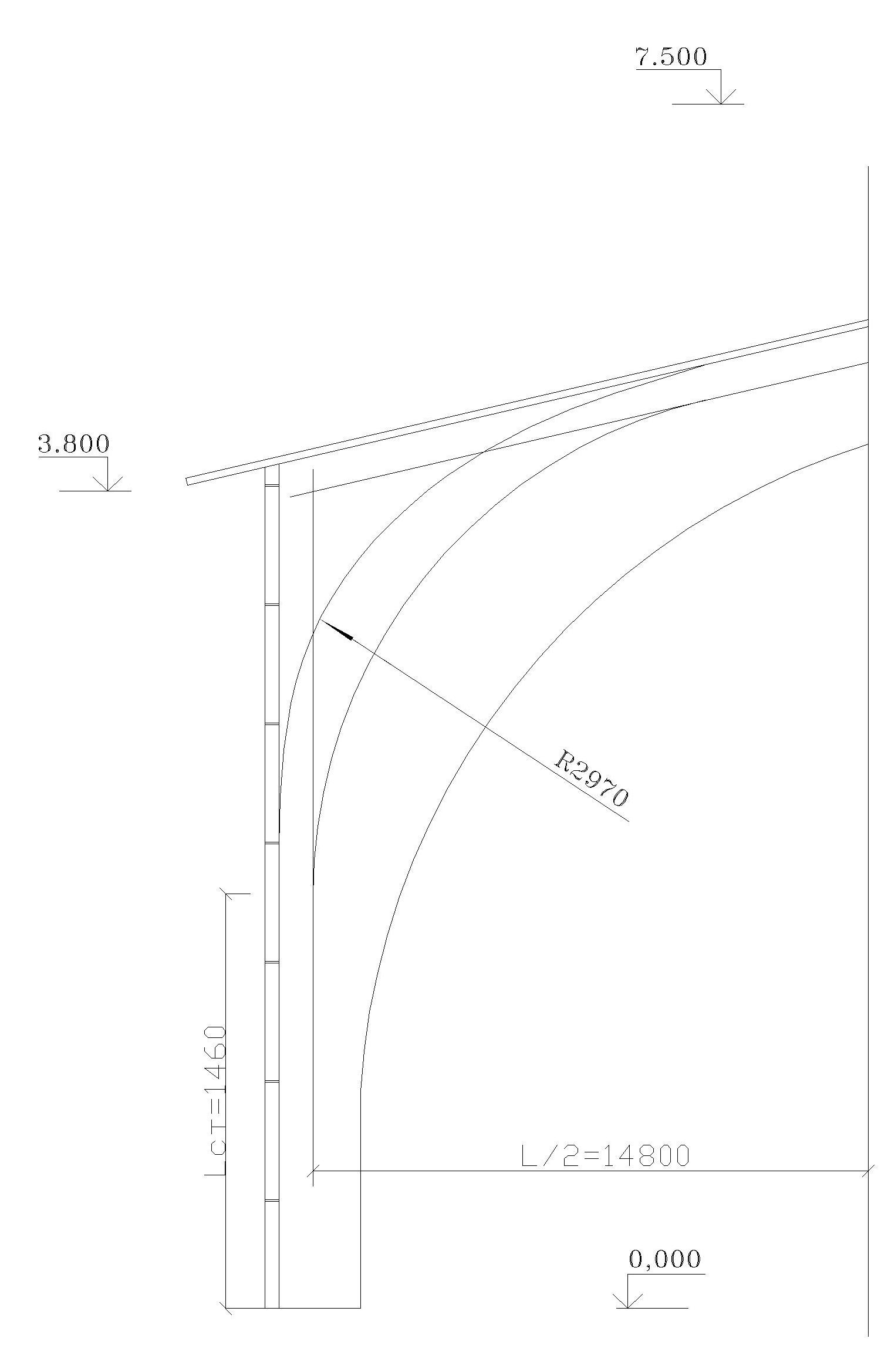

Проверка устойчивости плоской формы деформирования рамы

Рама закреплена из плоскости:

- в покрытии по наружной кромке плитами по ригелю;

- по наружной кромке стойки стеновыми панелями. Внутренняя кромка рамы не закреплена.

Точку перегиба моментов, т.е. координаты точки с нулевым моментом находим из уравнения моментов, приравнивая его к нулю:

;

;

;

;

Решая квадратное уравнение, получим:

;

;

принимаем , тогда

.

Точка перегиба эпюры моментов соответствует координатам от оси опоры и .

Тогда расчетная длина растянутой зоны, имеющей закрепления по наружной кромке равна: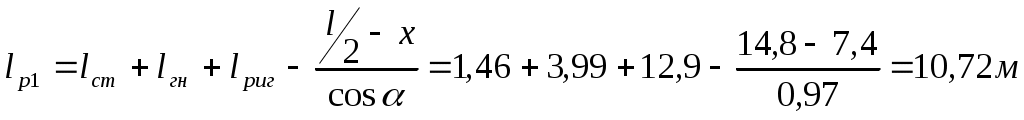

.

;
Расчетная длина сжатой зоны, наружной (раскрепленной) кромки ригеля (т.е. закреплений по растянутой кромке нет) равна: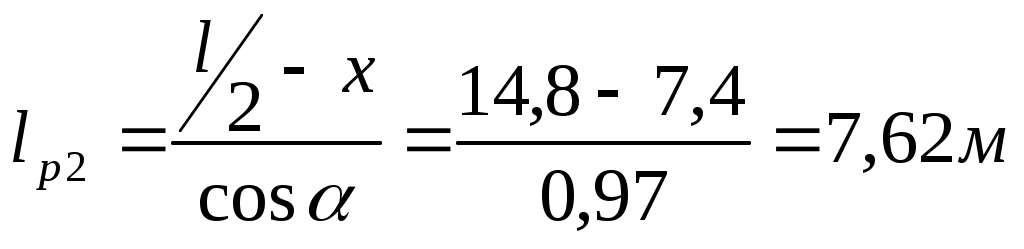

.

Таким образом, проверку устойчивости плоской фермы деформирования производим для 2-х участков.

Проверка устойчивости производится по формуле (33) СНиП II-25-80: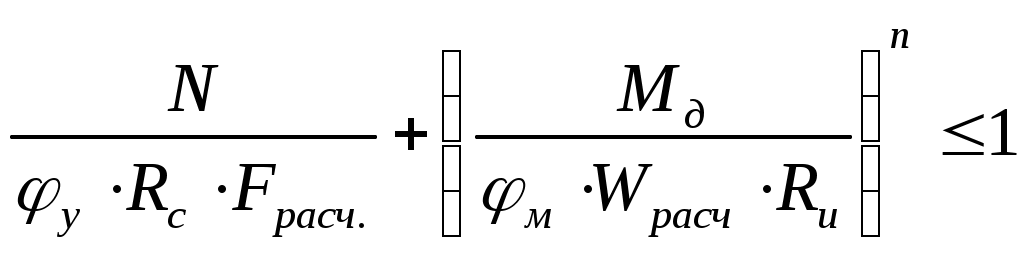

, , где :

– продольная сила на криволинейном участке рамы;

– изгибаемый момент, определяемый из расчета по деформированной схеме;

– коэффициент продольного изгиба, определяемый по формуле (8) СНиП II-25-80;

– коэффициент, учитывающий наличие закреплений растянутой зоны из плоскости

деформирования (в нашем случае n = 2, т.к. на данном участке нет закреплений растянутой зоны);

– коэффициент, определяемый по формуле (23) СНиП II-25-80.

1) Для сжатого участка находим максимальную высоту сечения из соотношения:

.



.

Найдем значение коэффициента по формуле (23) СНиП II-25-80:



– коэффициент, зависящий от формы эпюры изгибающих моментов на участке , определяемый по табл. 2 прил. 4 СНиП II-25-80 ( в данном случае равен 1,13).






Находим максимальный момент и соответствующую продольную силу на расчетной длине , при этом горизонтальная проекция этой длины будет равна



Максимальный момент будет в сечении с координатами: и ;








Момент по деформируемой схеме:

, ,

тогда , .

Так как , принимаем , где .

Коэффициент для по табл.7 СНиП II-25-80, тогда,

,

Подставим , .

При расчете элементов переменного по высоте сечения, не имеющих закреплений из плоскости по растянутой кромке или при числе закреплений , коэффициенты и – следует дополнительно умножать, соответственно, на коэффициенты и в плоскости (по табл. 1 и 2 Приложения 4 СНиП II-25-80):



.

Тогда



Подставим значения в формулу: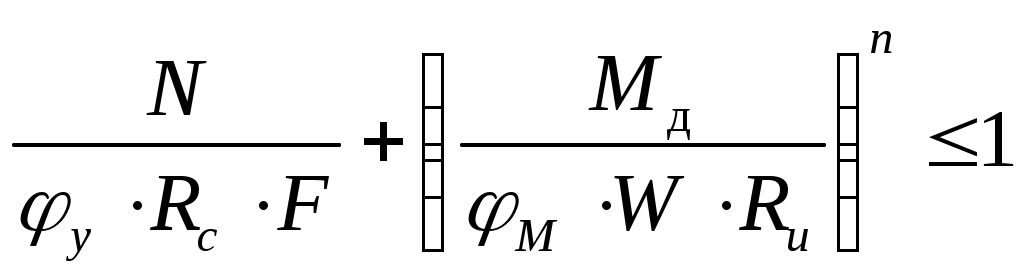



и получим:



2) Производим проверку устойчивости плоскости формы деформирования растянутой зоны на расчетной длине , где имеются закрепления растянутой зоны.

Гибкость:

;

Коэффициент :

;

Коэффициент :

.

При закреплении растянутой кромки рамы из плоскости, коэффициент необходимо умножать на коэффициент (формула 34 СНиП II-25-80), а – на коэффициент

(по формуле 24 того же СНиП).

Поскольку верхняя кромка рамы раскреплена прогонами и число закреплений ,

величину 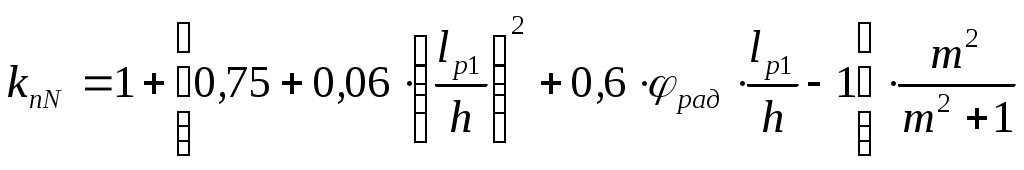следует принимать равной 1, тогда:

;

, где

, – количество закрепленных точек растянутой кромки.

;

.

Тогда расчетные значения коэффициентов и примут следующий вид:





Подставляя эти значения в исходную формулу проверки устойчивости плоской формы деформирования, получим: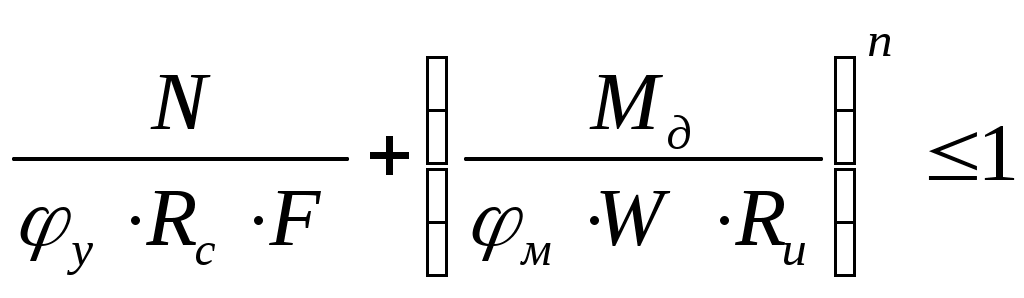



,

т.е. общая устойчивость плоской формы деформирования рамы обеспечена с учетом наличия закреплений по наружному контуру.