расчет четырехполюсника кр. расчет параметров четырехполюсника 5 вариант 3. расчет параметров четырехполюсника
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
«РАСЧЕТ параметров ЧЕТЫРЕХПОЛЮСНИКА» На рисунке заданы электрические схемы четырехполюсников, где цифрами обозначены номера элементов, а буквами а, в, с, д, е –исходные четырехполюсники. В таблице приведены данные исходных четырехполюсников, индуктивность L задана в мГн, емкость С в мкФ, цифрами без индекса заданы активные сопротивления в Ом. Внутреннее сопротивление источника Z01 = 50ej20 Ом и сопротивление нагрузки Z02 = 100 Ом для всех вариантов одинаковы. Частота входного сигнала f =500Гц. Требуется: 1) в соответствии с заданием нарисовать электрическую схему составного четырехполюсника (следует обратить внимание на последовательность соединения четырехполюсников при их каскадном соединении). Если исходные четырехполюсники записаны в следующем порядке «е, а, в», то следует к выходу четырехполюсника «е» подключить вход «а», а к его выходу подсоединить вход четырехполюсника «в»; 2)проверить регулярность параллельного соединения; 3)используя приведенные в теоретической части методы расчета матричных коэффициентов, определить A или Y-параметры исходных четырехполюсников; 4) при заданной частоте вычислить сопротивления Т или П-образных схем замещения составного четырехполюсника; 5)определить характеристические параметры составного четырехполюсника; 6)определить рабочий коэффициент передачи составного четырехполюсника, оценить уменьшение мощности только за счет четырехполюсника и за счет рассогласования между сопротивлениями источника и нагрузки; 7)определить для составного четырехполюсника затухание несогласованности по характеристическим сопротивлениям на входе и выходе его четырехполюсника; 8)в режиме холостого хода определить передаточную функцию по напряжению и построить амплитудно- и фазочастотную характеристики этой функции в диапазоне частот от 0 до 1200 Гц. Исходные типы четырехполюсников 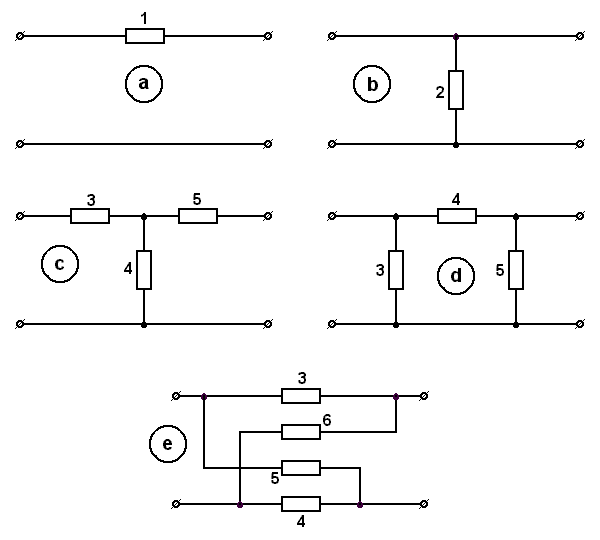
f=500 Гц 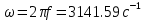 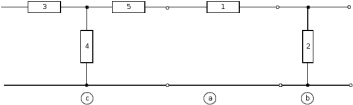  1. Определим комплексы сопротивлений 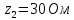 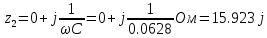  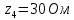 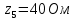 a) Рассмотрим четырехполюсник c Параметры этого четырехполюсника будем находить, как параметры T-образного четырехполюсника. 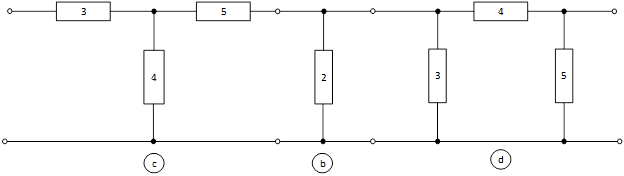 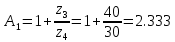 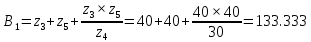 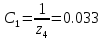 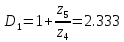 b) Рассмотрим четырехполюсник a  Параметры этого четырехполюсника будем находить, как параметры П-образного четырехполюсника, где два других сопротивления равны 0. 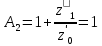 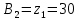 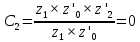 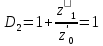 c) Рассмотрим четырехполюсник b 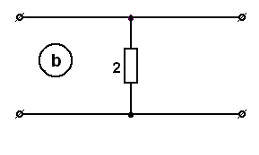 Параметры этого четырехполюсника будем находить, как параметры Т-образного четырехполюсника, где два других сопротивления равны 0. 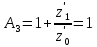  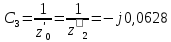 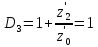 2) Вычислим при заданной частоте f = 500 Гц сопротивления Т-образной схемы замещения составного четырехполюсника, А-параметры Т-образной схемы замещения Найдем как произведения А - матриц четырехполюсников входящих в составной четырехполюсник. 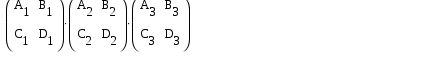  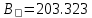 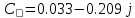 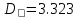  Определим сопротивления Т-образной схемы замещения. 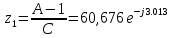 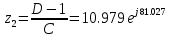 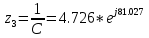 3) Определим характеристические параметры составного четырехполюсника Под параметрами подразумеваются два характеристических сопротивления 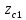 и и 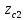 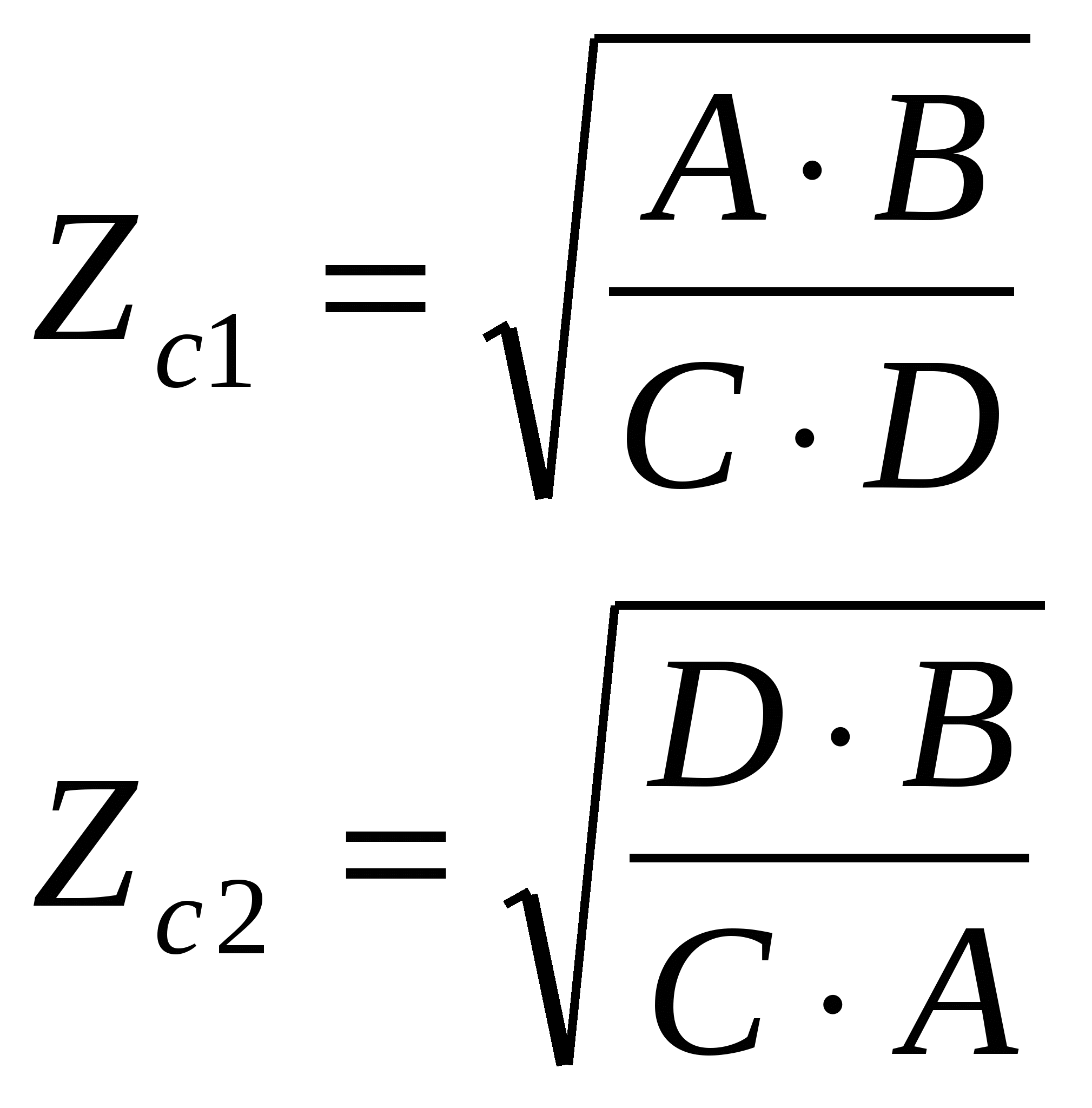 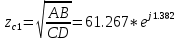 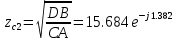 4) Рассчитаем рабочий коэффициент передачи составного четырехполюсника Для симметричного четырехполюсника имеем: 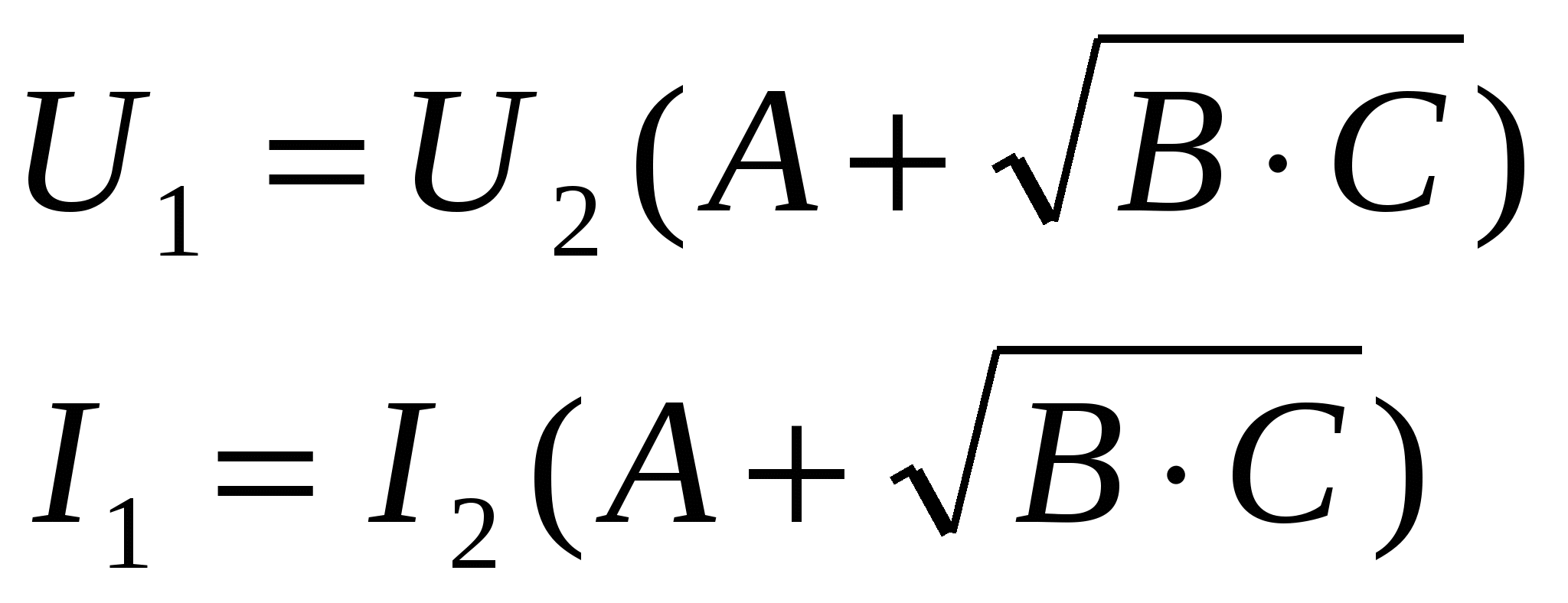 Комплексное число 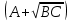 полагают равным полагают равным 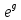 , где g = a + ib= =ln , где g = a + ib= =ln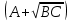 g – рабочий коэффициент передачи. 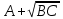 = =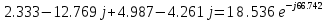 g = ln 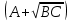 g = 2.733+j75.38 Величина a характеризует затухание составного четырехполюсника. а=2.919 5) Оценим уменьшение мощности только за счет четырехполюсника и за счет рассогласования между сопротивлениями источника и нагрузки Для того, чтобы оценить уменьшение мощности только за счет влияния четырехполюсника вводится понятие вносимого затухания 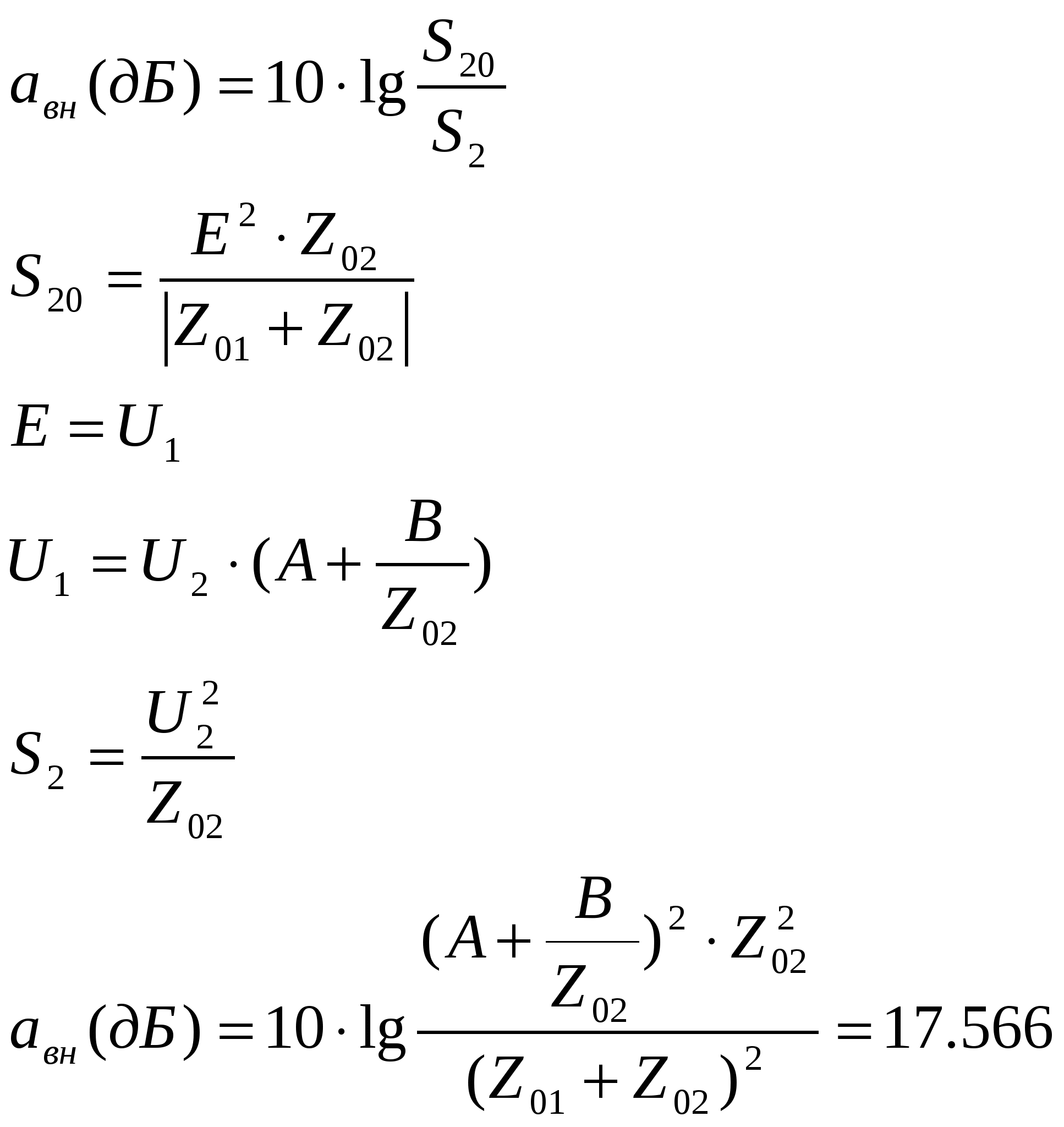 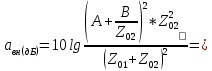 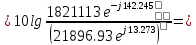   Уменьшение мощности за счет рассогласования между сопротивлениями Z01 и Z02 оценивается затуханием несогласованности 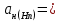 lg lg = lg = lg 6) Определим для составного четырехполюсника затухание несогласованности по характеристическим сопротивлениям на входе и выходе четырехполюсника 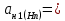 ln ln = ln = ln  ln ln = ln = ln 7) В режиме холостого хода построим передаточную функцию по напряжению и построим амплитудно- и фазочастотную характеристики этой функции 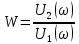 где 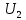 - напряжение на выходе четырехполюсника в режиме холостого хода. - напряжение на выходе четырехполюсника в режиме холостого хода.Эту передаточную функцию можно определить, если уравнения четырехполюсника записаны в А-форме, при I2=0 а) Амплитудночастотная характеристика W = 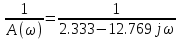 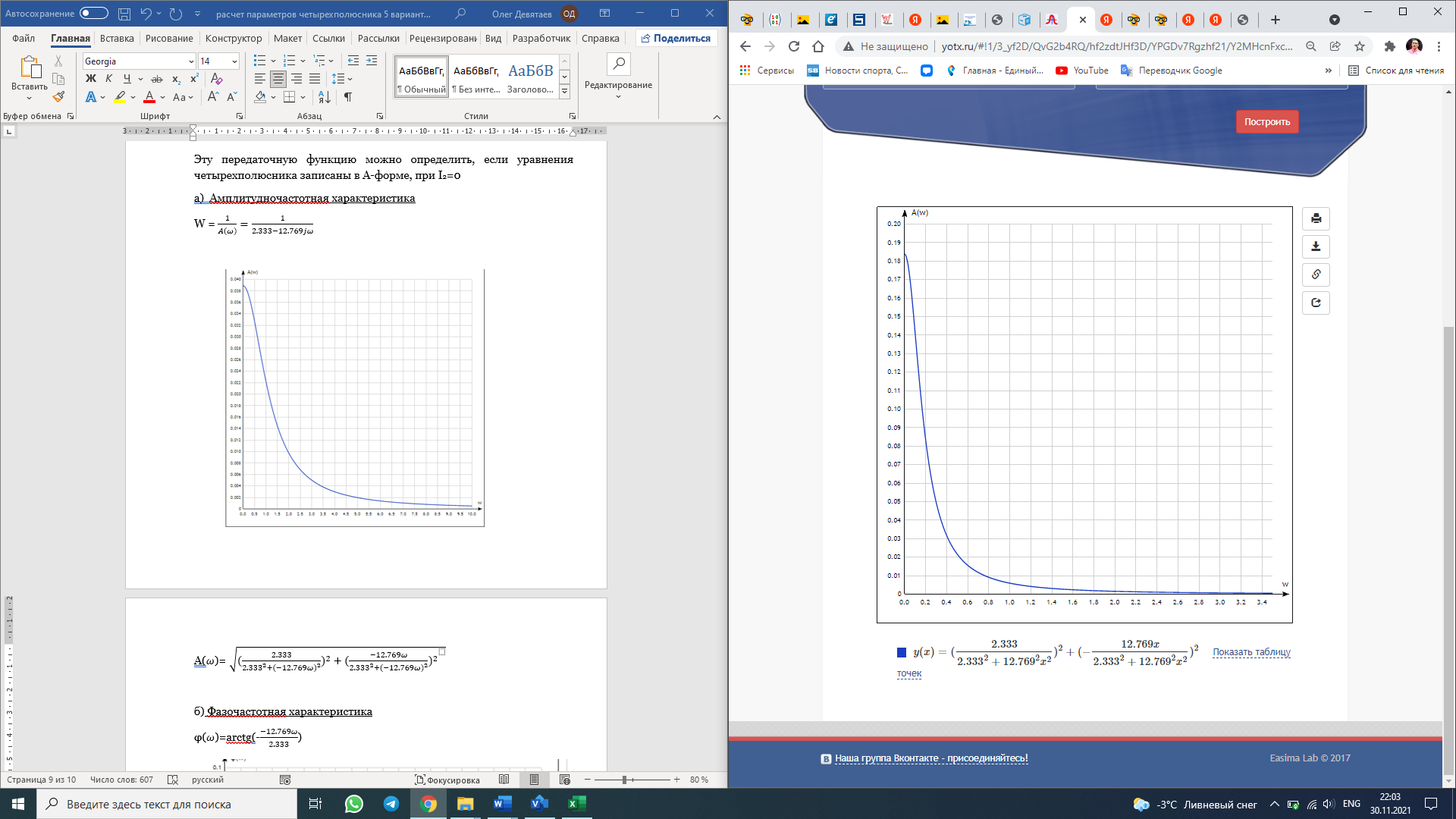 A( 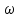 )= )= 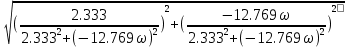 б) Фазочастотная характеристика 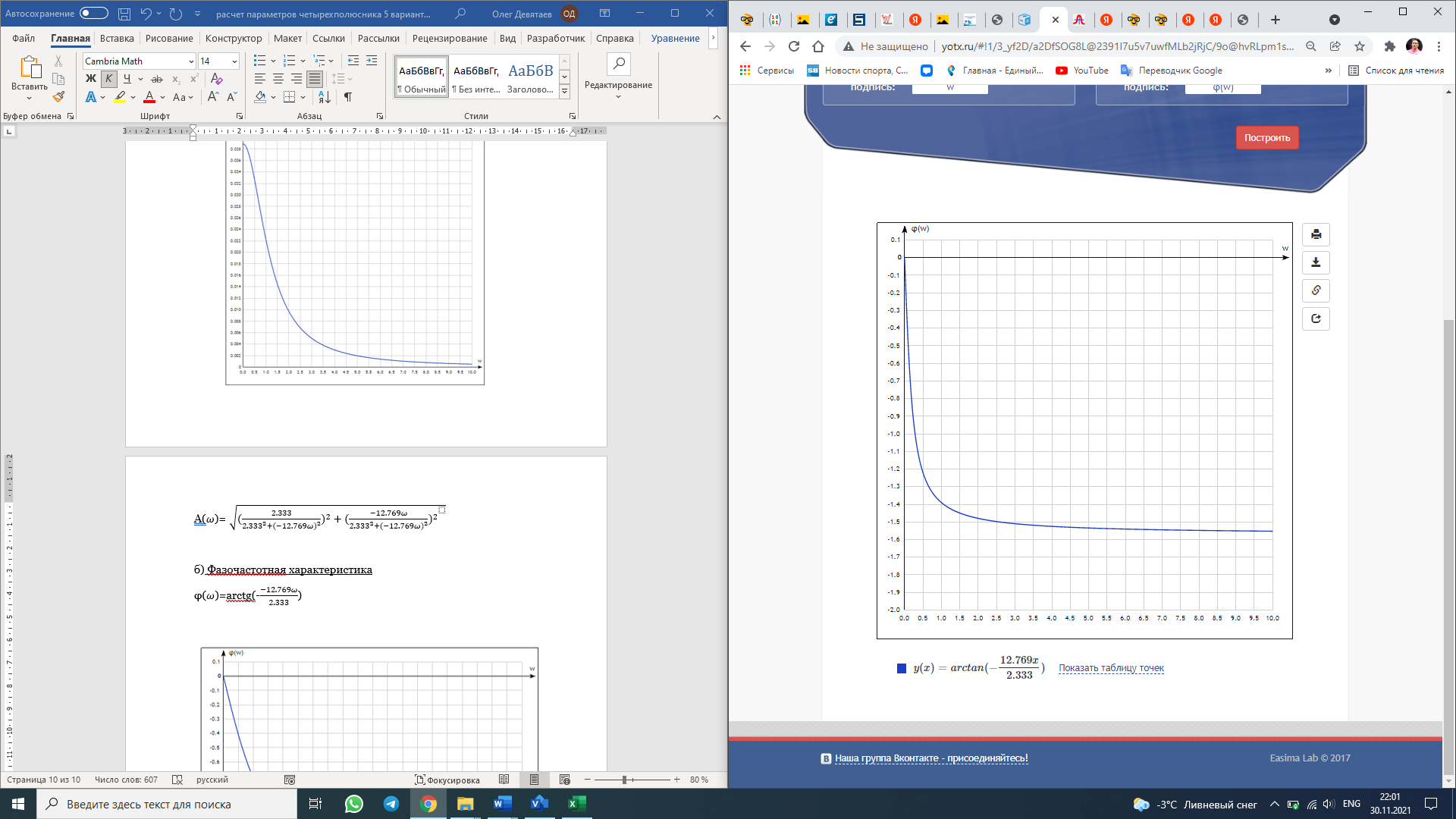 φ( φ(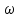 )=arctg(- )=arctg(-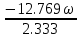 ) ) | ||||||||||||||||||||||||||
