Файл 1. Расчёт параметров однофазного

• Название: Расчёт параметров однофазного
• Дата: 07.09.2022
• Размер: 69.87 Kb.
• Имя файла: Файл 1.docx
• Тип: Задача; #666125

Задача№1.Расчёт параметров однофазного трансформатора

Однофазный трансформатор малой мощности характеризуется ^{следующими номинальными величинами: мощность S}н^{, первичное напряжение U}1н^{, вторичное напряжение U}2н^{, процентное значение тока холостого хода i}о ^{%, мощность потерь в сердечнике трансформатора P}о^{, процентное значение напряжения короткого замыкания u}k^{%, мощность потерь короткого замыкания P}кн^{. Числовые значения заданных величин} исходных данных для каждого из вариантов указаны в таблице 1.

Определить:

1. 
   Коэффициент трансформации трансформатора k, номинальные токи ^{первичной I}1н ^{и вторичной I}2н ^{обмоток.}
   
2. 
   Начертить схему замещения трансформатора и определить параметры
   

T-образной схемы замещения.

3. 
   КПД при коэффициенте нагрузки β = (0; 0,25;0,5;0,75;1,0) и ^{коэффициенте мощности cosφ}2 ^{= 0,8. На основании расчетов построить} зависимость η= f(β).
   
4. 
   Процентное изменение вторичного напряжения u% и вторичное ^{напряжение U}2 ^{при β = (0; 0,25;0,5;0,75;1,0) и cosφ}2 ^{= 0,8. На основании расчетов построить зависимость U}2 ^{= f(β).}
   
5. 
   Характер нагрузки, при котором вторичное напряжение не зависит от коэффициента β.
   

Решение1 .Коэффициент трансформации однофазного трансформатора:

^k=U1н ^{/ U}2н^{= 8590 / 115 = 74,7.}


1Н
Номинальный ток первичной обмотки:

I  S
1H H

U  1200 / 8590 = 0,14 A.

2Н
Номинальный ток вторичной обмотки:

I  S
2H H

U  1200 / 115 = 10,43 А.

2. 
   T-образная схема замещения однофазного трансформатора приведена на рисунке 2.1.
   

^r₁ х₁ ^x2 ^r₂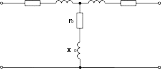


Рисунок 2.1 – T-образная схема замещения однофазного трансформатора

Определение параметров схемы замещения начинаем с расчёта тока холостого хода:

I ^iоIн ²⁰ 0,14  0, 03 А,

^о 100 100

тогда полное сопротивление намагничивающей ветви:

^zо ^{= U}1н ^/Iо ^{= 8590 / 0,03 = 286333 Ом.}

Активное сопротивление намагничивающей ветви:

Индуктивное сопротивление намагничивающей ветви:



Полное сопротивление короткого замыкания: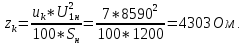



Активное сопротивление короткого замыкания:



Индуктивное сопротивление короткого замыкания: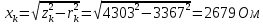

2. 
   КПД при коэффициенте нагрузки β = (0; 0,25;0,5;0,75;1,0) и ^{коэффициенте мощности cosφ}2 ^{= 0,8 можно определить из выражения:}
   

  1

P ² P

0 КН _.

Н 2 0 КН
S cos  P ² P

Результаты расчета КПД представлены в таблице 6.2.

Таблица2.2– Результаты расчета КПД

β	0	0,25	0,5	0,75	1
η	0	0,82	0,88	0,89	0,89

На основании результатов расчета, представленных в таблице 2.2,

построим зависимость η = f(β), представленную на рисунке 2.2.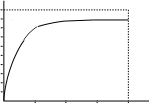

η

1

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1
0

^{0,25 0,5 0,75} 1 ^β

Рисунок 2.2 – Зависимость η = f(β)

2. 
   Процентное изменение вторичного напряжения u% и вторичное ^{напряжение U}2 ^{при β = (0; 0,25;0,5;0,75;1,0) для активно-индуктивной нагрузки cosφ}2 ^{= 0,8определяем, используя выражение:}
   

1н к 2 к 21н

^{ I rcos  Ixsin  }  ^u% 

 u%   _{ }100 %, U₂  _1

^U2н^.

 ^U1н 

_ 100% _

^{Результаты расчета u% и U}2 ^{представлены в таблице 2.3.}

Таблица2.3– Результаты расчета КПД

β	0	0,25	0,5	0,75	1
u%	0	1,74	3,48	5,22	6,96
U2, В	24	23,58	23,16	22,75	22,33

На основании результатов расчета, представленных в таблице 2.3, ^{построим зависимость U}2 ^{= f(β), представленную на рисунке 2.3.}

U₂ , В

25
20
15
10
5
^{0 0,25} 0,5 0,75 1 ^β

Рисунок 2.3 – Внешняя характеристика однофазного трансформатора

^{4. Напряжение U}2 ^{на зажимах вторичной обмотки не будет зависеть от} коэффициента нагрузки β при выполнении условия

I_1н r_к cos₂  I_1н x_к sin ₂  0,

^{значит tgφ}2 ^{= – r}к^/xк^.

Отрицательный знак в правой части уравнения указывает на активно- емкостной характер нагрузки, а величина угла

^φ2 ^{= – arctg (r}к^/xк^{) = – arctg (11,62/6,98) = – 59°.}