Расчет преднапряженного элемента. Пример расчета преднапряженного элемента (1). Расчет плиты на общий изгиб
 Скачать 99.36 Kb. Скачать 99.36 Kb.
|
|
Расчет плиты на общий изгиб осуществляется как однопролетной балки, опорами которой являются стропильные балки. Расчетный пролет плиты: l0= 5,86 м. Погонная расчетная нагрузка на плиту: q = (4,2 + 1,54)  3 = 17,22 кН/м. 3 = 17,22 кН/м.Максимальный расчетный момент в нормальном сечении: Мmax = ql02/8 = 17,22  5,862/8 = 73,92 кНм. 5,862/8 = 73,92 кНм.Максимальная расчетная поперечная сила: Qmax =ql0/2 = 17,22  5,86/2 = 50,45 кН. 5,86/2 = 50,45 кН.Нормальные сечения. Расчетным является тавровое сечение с полкой в сжатой зоне (рис. В6). Суммарная ширина ребра b = 2(75 + 105)/2 = 180 мм, расчетная ширина полки b'f = 2l0/6 + b = 2  5860/6 + 180 = 2133 мм, ее высота h'f = 30 мм. Предварительно назначим расстояние от нижней грани ребра до оси продольной арматуры a= 30 мм, тогда рабочая высота сечения h0 = 270 мм. 5860/6 + 180 = 2133 мм, ее высота h'f = 30 мм. Предварительно назначим расстояние от нижней грани ребра до оси продольной арматуры a= 30 мм, тогда рабочая высота сечения h0 = 270 мм.Проверим положение нейтральной оси: Mf = Rbb'fh'f (h0 – 0,5h'f) = 15,3  2133∙30(270 – 0,5 2133∙30(270 – 0,5 30) = 249,7106 Нмм = 249,7 кН∙м > 73,92 кН∙м, т.е. нейтральная ось проходит в полке, и дальнейший расчет осуществляется как для прямоугольного сечения шириной b'f. 30) = 249,7106 Нмм = 249,7 кН∙м > 73,92 кН∙м, т.е. нейтральная ось проходит в полке, и дальнейший расчет осуществляется как для прямоугольного сечения шириной b'f.Вычислим значение αmR с учетом влияния на относительные деформации растянутой арматуры предварительного напряжения арматуры. Предварительно примем напряжения в арматуре с учетом всех потерь равными σsp = 0,4Rs,ser = 0,4∙800 = 320 МПа. В этом случае Ɛs,el = (Rs + 400 – σsp)/Es = (695 + 400 – 320)/200000 = 0,003875; значение ξR = 0,8/(1 + Ɛs,el/Ɛb2) = 0,8/(1 + 0,003875/0,0035) = 0,397; значение αmR = ξR(1 – 0,5 ξR) = 0,397  (1– (1– 0,5∙0,397) = 0,318. 0,5∙0,397) = 0,318.Определим коэффициент αm = M/(Rbbho2) = 73,92106/(15,3  2128 2128 272) = 0,033 < αmR. Требуемая площадь сечения продольной рабочей арматуры: 272) = 0,033 < αmR. Требуемая площадь сечения продольной рабочей арматуры: As= Rb b'fh0 ( 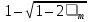 )/Rs = )/Rs == 15,3  2133∙27 2133∙27 (1 (1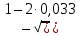 /695 = 426 мм2, /695 = 426 мм2,где Rs = 695 МПа расчетное сопротивление растяжению арматуры класса А800. Примем по одному стержню 18A800 в каждом продольном ребре с суммарной площадью сечения Asp = 509 мм2.Так как рабочая высота сечения не уменьшилась, а площадь сечения фактически принятой арматуры больше расчетной, проверку несущей способности проводить не требуется. Процент армирования сечения µ = [As/(bh0)]100% = [509/(175270)]  100 % = 1,08 % > 0,1 %, что удовлетворяет требованиям СП [4]. 100 % = 1,08 % > 0,1 %, что удовлетворяет требованиям СП [4].Наклонные сечения. Расчёт наклонных сечений выполним без учета усилия предварительного обжатия. Поперечная арматура – класса А500С с расчетным сопротивлением растяжению Rsw = 300 МПа. Предварительно назначим минимальный диаметр поперечных стержней (хомутов) 6 мм с площадью сечения в двух ребрах Asw = 57 мм2. Максимально допустимый шаг s = h0/2 = 271/2 = 136 мм. Принимаем с округлением s = 100 мм. Погонная несущая способность поперечной арматуры: qsw = RswAsw /s = 300  57/100 =171 Н/мм > qsw,min = 0,25Rbt 57/100 =171 Н/мм > qsw,min = 0,25Rbt b = 0,25 b = 0,25 1,035 1,035 180 = 46,6 Н/мм. 180 = 46,6 Н/мм.Проекция опасного наклонного сечения: с = 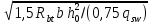 = == 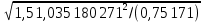 = 400 мм. = 400 мм.Условия СП [4]) выполняются, как для арматуры (с 2h0 = 542 мм и с h0 = 271 мм), так и для бетона (с 3h0и с 0,6h0). Поперечная сила, воспринимаемая бетоном сжатой зоны над вершиной наклонной трещины: Qb = (1,5Rbtbh02)/с = (1,5  1,035 1,035 180∙2712)/400 = 180∙2712)/400 =51,3103 Н = 51,3 кН Поперечная сила, воспринимаемая поперечными стержнями при расчетной проекции наклонного сечения: Qsw= 0,75qswc = 0,75  171 171 400 = 51,3103 Н = 51,3 кН. 400 = 51,3103 Н = 51,3 кН.Несущая способность наклонного сечения: Qu=Qb+ Qsw = 102,6 кН При ширине верхнего пояса стропильной балки 240 мм глубина опирания плиты lsup = 240/2 – 10 = 110 мм. Опорную реакцию Qmax считаем приложенной посередине lsup. Тогда расчетная поперечная сила в опасном сечении Q = Qmax – q(0,5lsup + c) = 50,45 – 17,22(0,055 + 0,4) = 42,61кН. Q Qu, прочность обеспечена. Проверим несущую способность наклонного сечения при действии изгибающего момента из условия: M ≤Ms + Msw, где M – момент в вершине наклонного сечения от расчетной нагрузки, Ms, и Msw – моменты, воспринимаемые соответственно продольной арматурой и поперечными стержнями, пересекаемыми наклонным сечением, относительно оси, проходящей через точку приложения равнодействующей усилий в сжатой зоне бетона. Предельное усилие в напрягаемой арматуре Nsp= sRsAsp, где коэффициент s учитывает снижение несущей способности арматуры вследствие недостаточной ее заделки в бетоне. Принимают коэффициент меньшим из двух значений: s = lx/lp и s= lx/lan, где lx – длина фактической заделки арматуры в бетоне, lp = sp1 Asp/(Rbondus); – длина зоны передачи напряжений, lan = Rs Asp/(Rbond us), – длина зоны анкеровки, Rbond = 12Rbt, 1 = 2,5 – коэффициент для стержневой арматуры периодического профиля, 2 = 1,0 – коэффициент для напрягаемой арматуры, us = 56,5 мм – периметр сечения стержня диаметром 18 мм, sp1 – величина предварительного напряжения арматуры за вычетом первых потерь, Asp = 254,5 мм2 – площадь сечения стержня диаметром 18 мм. Величина контролируемого напряжения в стержнях sp = 0,6Rsn = 0,6800 = 480 МПа, что даже без учета потерь заведомо меньше величины Rs = 695 МПа. Поэтому для нахождения s используем длину зоны анкеровки: lan = 695245,5/(2,51,03556,5) = 1164 мм. Внутренняя грань опоры находится на расстоянии 110 мм от торца плиты (длина опирания lsup,рис. В5), начальная линия пересечения наклонного сечения с равнодействующей усилия в стержнях Ns проходит под углом 45о, т.е. на расстоянии от грани 29 мм (оно равно величине а – см. выше). Для улучшения анкеровки на концевых участках стержней высажены головки (рис. 63,б), которые удлиняют заделку в бетоне на условную велич 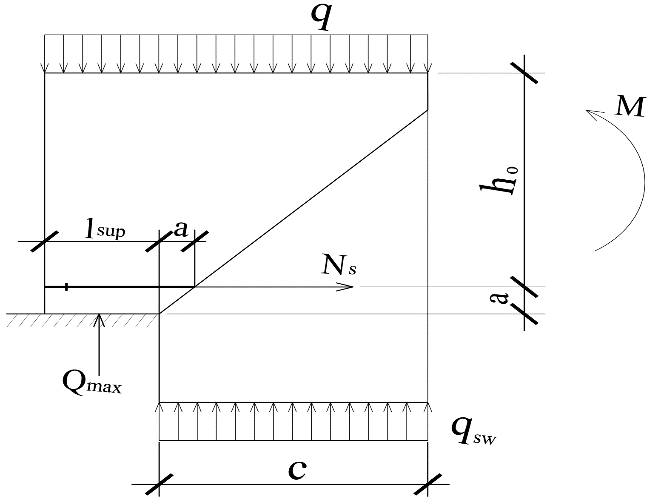 ину lan = 2ds = 36 мм (табл. 18). В итоге длина заделки напрягаемой арматуры в бетоне lx = 110 +29 + 36 = 175 мм. Отсюда s = 175/1164 = 0,15, предельное усилие в арматуре Ns= 0,15695509 = 53,2103 Н = 53,2 кН. Момент, воспринимаемый продольной арматурой: ину lan = 2ds = 36 мм (табл. 18). В итоге длина заделки напрягаемой арматуры в бетоне lx = 110 +29 + 36 = 175 мм. Отсюда s = 175/1164 = 0,15, предельное усилие в арматуре Ns= 0,15695509 = 53,2103 Н = 53,2 кН. Момент, воспринимаемый продольной арматурой:  Рис. В5 27 Ms = Nsz = 53,20,90,271 = 13,0 кНм, где z = 0,9h0. Проекция опасного наклонного сечения [18]: с = Qmax/(q + qsw) = 50,45/(17,22 + 171) = 0,269 м, что меньше минимально допустимой величины c= h0 = 271 мм. Принимаем c= 271 мм. Момент, воспринимаемый поперечной арматурой: Msw = qswc2/2 = 1710,2712/2 = 6,23 кНм. Несущая способность сечения: Мu = Ms + Msw = 19,23 кНм. Момент от расчетной нагрузки М = Qmax(lsup/2 + c) – q(lsup/2 + c)2/2 = 50,45(0,055 + 0,271) – 17,22(0,055 + 0,271)2/2 = 15,53 кНм. М Мu, прочность достаточна. 2. Расчет по трещиностойкости Геометрические характеристики приведенного сечения определим исходя из размеров, указанных на рис. В6. При определении характеристик учтем только растянутую арматуру, т.к. сетка в сжатой зоне конструктивно не защищена от потери устойчивости. Напрягаемая арматура Asp = 0,000509 м2. Начальный модуль упругости бетона Eb = 32500 МПа, модуль упругости арматуры Es = 200000 МПа. Коэффициент приведения: αs = Es/Eb = 200000/32500 = 6,15. Площадь приведенного сечения: Ared = 213330 + 180270 + 5096,15= 115,72103 мм2. Статический момент сечения относительно нижней грани ребра: Sred = 213330(270 + 30/2) + 180270135 + 5096,1529 = (16317,45 + 6561+ 90,8)103 = 22969103 мм3 Расстояние от центра тяжести сечения до нижней грани у = Sred/Ared = 22969103/115,72103 = 198,5 мм, до верхней грани у = h – y = 300 – 198,5 = 101,5 мм. 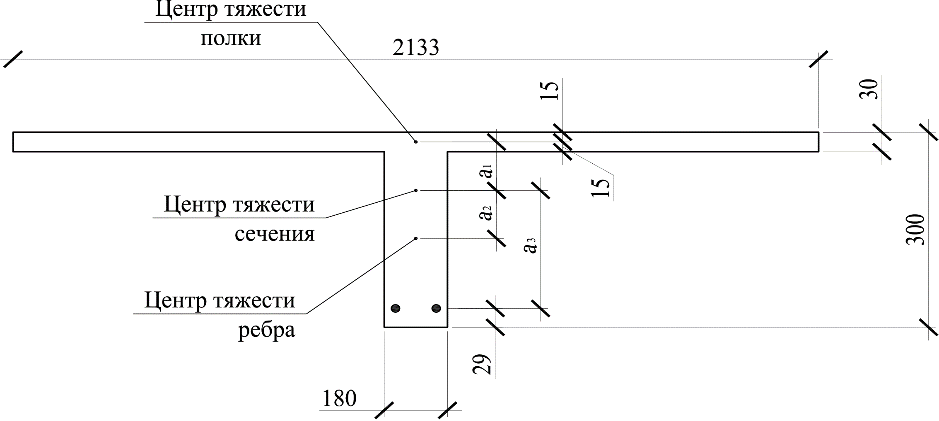 Рис. В6 Расстояния от центра тяжести всего сечения до центра тяжести сечения верхней полки а1= 300 – 198,5 – 15 = 86,5 мм, до центра тяжести сечения ребра а2 = 198,5 – 135 = 63,5 мм, до оси арматуры а3 = 198,5 – 30 = 168,5 мм (рис. В6): Момент инерции приведённого сеченияIred: Ired = 2133303/12 + 21333086,52 + 1802703/12 + 18027063,52 + 5096,15168,52 = (4,8 + 478,8+ 295,0 + 196 + 88,9)106 = 1063,5106 мм4. Упругий момент сопротивления приведенного сечения относительно нижней грани Wred, = Ired/y= 1063,5106/198,5 = 5358103 мм. То же, относительно верхней грани Wred, = Ired/y = 1063,5106/101,5 = 10478103 мм. Упруго-пластические моменты сопротивления (п.8.2.11 СП [4]): Wpl = 1,3Wred, = 5358103  1,3 = 6965103 мм3, 1,3 = 6965103 мм3,Wpl = 1,3Wred= 10478103  1,3 = 13621103 мм3. 1,3 = 13621103 мм3.Расстояния от центра тяжести сечения до верхней r и нижней r ядровых точек: r= Wred,b/Ared = 6965103 /115,72103 = 60,2 мм, r = Wred,t/Ared = 13621103 /115,72103 = 117,7 мм. Потери напряжений в арматуре. Начальная величина предварительного напряжения арматуры: σsp = 0,6Rs,ser = 0,6  800 = 480 МПа, 800 = 480 МПа,где Rs,ser– нормативное сопротивление арматуры растяжению. Арматура натягивается электротермическим способом на упоры формы. Кубиковая передаточная прочность бетона (в момент отпуска арматуры) Rbp= 0,7В = 21 МПа Потери от релаксации напряжений: ∆σsp1 = 0,03 σsp = 480  0,03 = 14,4 МПа. 0,03 = 14,4 МПа.Т. к. натяжение осуществляется на упоры форм, потери от температурного перепада ∆σsp2 отсутствуют. Потери от деформаций форм ∆σsp3, деформаций анкеров натяжных устройств ∆σsp4 при электротермическом способе не определяют, т.к. их учитывают при назначении заготовочной длины стержней. Потери от усадки бетона: ∆σsp5 = εb,sh Es0,85, = 0,0002  200000 200000 0,85 = 34 МПа, 0,85 = 34 МПа,где εb,sh – относительные деформации усадки бетона классов В35 и ниже, 0,85 – коэффициент, принимаемый при тепловой обработке изделий. Потери от ползучести бетона: ∆σsp6 = (0,8 αs φb,cr ϭbp)/[1+ αs µsp(1+ y2Ared/Ired)(1+ 0,8 φb,cr)], где φb,cr= 2,74 – коэффициент ползучести бетона при Rbp= 21 МПа (табл. 6.1.2 СП[4]), ϭbp = Р(1)/Ared + Р(1) eop y/Ired – Мsvy/Ired – напряжения в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия Р(1), определяемое с учётом первых потерь, eop = 168,5 мм – эксцентриситет усилия Р(1) относительно центра тяжести сечения. Р(1) = (σsp – ∆σsp1)Asp = (480 – 14,4)  509 = 237∙103 Н = 237 кН; 509 = 237∙103 Н = 237 кН;При однорядном расположении напрягаемой арматуры и отсутствии ненапрягаемой расчетной арматуры расстояние от центра тяжести сечения до центра тяжести арматуры у = eop = 168,5 мм. Мsv = (gp/lp)γf lp2/8= (27/5,97)0,9∙5,972/8 = 18,13 кН∙м – момент от собственного веса плиты при обжатии после распалубки, где, gp – вес плиты; lp – длина плиты, а также ее расчетный пролет при выгибе при обжатии; γf = 0,9 – коэффициент надежности по собственному весу плиты, т.к. собственный вес снижает напряжения при обжатии ϭbp. Напряжения в бетоне при обжатии: ϭbp = Р(1)/Ared + Р(1) eop y/Ired – Мsv y/Ired = 237/(115,72103) + 237  168,5∙168,5/(1063,5106) – 18,13103 168,5∙168,5/(1063,5106) – 18,13103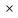 168,5/(1063,5106) = 0,0055 кН/мм2 = 5,5 МПа. 168,5/(1063,5106) = 0,0055 кН/мм2 = 5,5 МПа. ϭbp 0,9Rbp = 0,9∙21 = 18,9 МПа. Потери от ползучести бетона: ∆σsp6 = (0,8∙6,15  2,74 2,74 5,5)/{1 + [6,15 5,5)/{1 + [6,15 0,021 0,021 (1 + 198,52 (1 + 198,52 115,72103/(1063,5106)]∙(1 + 0,8 115,72103/(1063,5106)]∙(1 + 0,8 2,74)} = 38,2 МПа. 2,74)} = 38,2 МПа.Полные потери ∆σsp(2): ∆σsp(2) = ∆σsp1 +∆σsp5 + ∆σsp6 = 14,4 + 34 + 38,2 = 86,6 МПа < 100 МПа. Для дальнейших расчетов принимаем ∆σsp(2) = 100 МПа. Усилие обжатия при полных потерях Р(2): Р(2) = (480 – 100)  509 = 193,4103 Н = 193,4 кН. 509 = 193,4103 Н = 193,4 кН.Расчет по образованию трещин. Момент трещинообразования: Mcrс = Rbt,serWpl+ Р(2) erр = 1,75∙10–3∙6965103 + 193,4∙228,7 = 56380,7 кН∙мм = 56,38 кН∙м, где Rbt,ser = 1,75 МПа – нормативное сопротивление бетона растяжению, erр= eop + r = 168,5 + 60,2 = 228,7 мм – расстояние от силы обжатия до ядровой точки. Момент от полных нормативных нагрузок. Мn = qnlo2/8 = 4,59  3 3 5,862/8 = 59,1кН∙м 5,862/8 = 59,1кН∙м Мn > Mcrс = 56,38 кН∙м. Трещины образуются. Расчет по раскрытию трещин. Ширина продолжительного раскрытия трещин: acrc = acrc1, непродолжительного раскрытия трещин: acrc = acrc1 +acrc2 – acrc3, где acrc1 – ширина раскрытия трещин от продолжительного действия нормативных постоянных и временных длительных нагрузок; acrc2 – то же, от непродолжительного действия нормативных полных нагрузок; acrc3 – то же, от непродолжительного действия постоянных и временных длительных нагрузок. Ширину раскрытия трещин в зависимости от характера действующих нагрузок определяют по формуле: acrc = φ1 φ2 φ3 ψs (σs/Es) ls, где φ1 – коэффициент, учитывающий продолжительное действие нагрузок (при действии постоянных и длительных нагрузок, равный 1,4; при непродолжительном действии равный 1); φ2 – коэффициент учитывающий профиль арматуры (для стержней периодического профиля равный 0,5); φ3 – коэффициент, учитывающий характер нагружения (для изгибаемых элементов равный 1); ψs – коэффициент, учитывающий неравномерное распределение относительных деформаций растяжения арматуры между трещинами (согласно п. 8.2.15 [4] допускается принимать равным 1); ls – расстояние между трещинами. Напряжения в арматуре от постоянных и длительных нагрузок: σsl = [Mpnl (h0 – yc)/Ired,b – Р(2) /Ared,b] αsl, где, кроме ранее указанных обозначений, Mpnl – момент от нормативных постоянных и длительных нагрузок с учётом усилия обжатия; Ired,b – приведенный момент инерции сечения с учётом работы только сжатой части сечения и растянутой арматуры; αsl = Es/Eb,red – коэффициент приведения с учётом ползучести бетона; Eb,red = (Rbn/εb1,red); Rbn = 22 МПа– нормативное сопротивление бетона сжатию; εb1,red = 0,0015 – относительные деформации ползучести. Eb,red = 22/0,0015 = 14666,7МПа, αsl = 200000/14666,7 = 13,64, Mpnl = Мl – Р(2)e0p, Мl = qnll02/8 = (3,49+0,75)  3 3 5,862/8 = 54,6 кН∙м – момент от постоянных и длительных нормативных нагрузок. 5,862/8 = 54,6 кН∙м – момент от постоянных и длительных нормативных нагрузок.Mpnl = 54,6 – 193,4∙0,1685 = 22,01 кН∙м. Определим Ired,b, с учетом схемы на рис. В7, уточнив расстояние у от наиболее растянутого волокна бетона до центра тяжести сечения: у = Sred/Ared = 22969103/115,72103 = 198,5 мм. Высота сжатой части сечения: ус = 300 – 198,5 = 101,5 мм. Определим параметры Ired,b и Ared,b с учетом только сжатой зоны бетона и растянутой арматуры. Ared,b = 2133∙30 + 71,5∙180+ 509∙13,64 = 83,8∙103 мм2. Статический момент сжатой зоны относительно оси x0, проходящей через нейтральную ось: Sred,b = 2133∙30(101,5 – 15) + 71,5∙180∙35,75 – 509∙13,64  (270 – 101,5) = 4825∙103 мм3. (270 – 101,5) = 4825∙103 мм3.Центр тяжести: уcb= Sred,b/Ared,b= 4825∙103/83,8∙103 = 57,6 мм. Момент инерции: Ired,b = 2133∙303/12 + 30∙2133∙28,92 + 180∙71,53/12 + 180∙71,9∙13,92 + 509∙13,64  226,12 = 416∙106 мм4. 226,12 = 416∙106 мм4.Напряжения в арматуре от постоянных и длительных нагрузок с учётом преднапряжения: σsl= [18,6∙103(270 – 101,5)/ 416∙106 – 193,4/83,8∙103]  13,64 = 0,0713 кН/мм2 = 71,3 МПа. 13,64 = 0,0713 кН/мм2 = 71,3 МПа.Напряжения допустимы, т.к. не превышают значения Rs,ser – 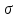 sp = 800 – 380 = 420 МПа. sp = 800 – 380 = 420 МПа.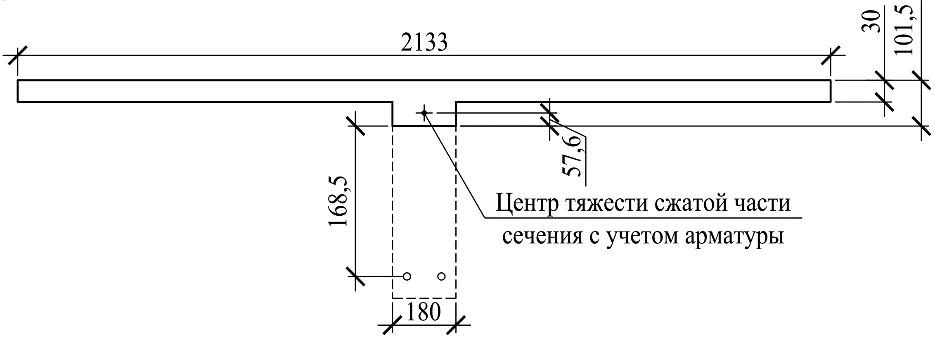 Рис. В7 Расстояние между трещинами: ls= 0,5Abt/Asds где, кроме ранее оговоренных, ds – диаметр продольной рабочей арматуры; Abt – площадь растянутой части сечения: Abt = bmryt, = 180∙150 = 27000 мм2, ytпринимают не более 0,5h (yt = 0,5∙300 = 150 мм – эту величину и примем для дальнейших расчетов). ls = 0,5  27000/509∙18 = 477 мм. Т.к. ls 400мм, для дальнейших расчетов принимаем ls = 400 мм. 27000/509∙18 = 477 мм. Т.к. ls 400мм, для дальнейших расчетов принимаем ls = 400 мм.Ширина продолжительного раскрытия трещин: acrc1 =1,4  0,5 0,5 1 1 1(71,3/200000) 1(71,3/200000) 400 = 0,1 мм < 0,2 мм. 400 = 0,1 мм < 0,2 мм.Поскольку кратковременные нагрузки малы (они составляют лишь 50% от снеговой нагрузки) и напряжения σs в арматуре при полных нормативных нагрузках возрастут незначительно, расчет по раскрытию трещин при непродолжительном действии нагрузок не производим в связи с заведомо положительным результатом. 3. Расчет по деформациям (прогибам) Для определения прогибов определим кривизну оси с учетом раскрытия трещин по формуле: (1/ρ) = (1/ρ)1 – (1/ρ)2 + (1/ρ)3, где (1/ρ)1 – кривизна оси от непродолжительного действия всей нагрузки; (1/ρ)2 – кривизна оси от непродолжительного действия постоянной и временной длительной нагрузки; (1/ρ)3 – кривизна оси от продолжительного действия постоянных и временных длительных нагрузок. Кривизну от соответствующих нагрузок определяют по формуле: (1/ρ) = (M – P(2) zp) /[(Es,red As z(h0–xN)], где, кроме ранее указанных, М – момент от соответствующих нагрузок; zp– расстояние от точки приложения усилия предварительного обжатия до точки приложения равнодействующей усилий в сжатой зоне; z – то же от центра тяжести растянутой арматуры (в данном случае, zp = z); Es,red = Es при ψs = 1.– приведённый модуль деформаций арматуры с учётом влияния растянутого бетона; xN – высота сжатой зоны с учётом влияния предварительного обжатия. В соответствии с 9.3.15 СП [4] примем zp = z = h0 – 0,3h0 = 270 – 0,3  270 = 189 мм и уточним значение с учётом таврового сечения. 270 = 189 мм и уточним значение с учётом таврового сечения.Высоту сжатой зоны xN при непродолжительном действии всей нормативной нагрузки определим с учетом момента Mp = 59,1 – 193,4∙0,1685 = 26,58 кН∙м и αs2 = 200000/14666,7 = 13,64: xN = h0[ 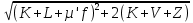 – (K +L+ µ'f)], – (K +L+ µ'f)],где К = µs(1 + z(P(2)/Mpnl)αs2 = [509/(180∙270)(1 + 189∙193,4/(22,01∙103)]13,64 = 0,385, µ's= 0 из–за отсутствия сжатой арматуры; L = µ'sαs1 = 0; V = µ's αs1 a1/h0 = 0; µ'f = A'f/(b h0); A'f= (2133 – 180)  30 = 58590 мм2 – площадь сечения свесов; 30 = 58590 мм2 – площадь сечения свесов; µ'f = 58590/(180∙270) = 1,21; Z= µ'f h'f/(2h0) = 1,21∙30/(2∙270 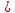 = 0,067. = 0,067.xN = 270  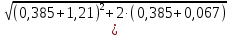 – (0,385 + 1,21)] = 70,74 мм. – (0,385 + 1,21)] = 70,74 мм.Кривизна оси: (1/ρ)1 = (M – P(2) zp)/[(Es,redAsz(h0– xN)] = (59,1∙103– 193,4∙189): [(200000∙10-3∙509∙189(270 – 70,74)] = 0,00000588 мм-1. Высоту сжатой зоны xN при непродолжительном действии постоянных и длительных нормативных нагрузок определим с учетом момента Mp = 54,6– 193,4∙0,1685 = 22,01 кН∙м и αs2 = 200000/14666,7 = 13,64: К = [509/(180∙270)  (1 + 189∙193,4/(22,01∙103)] 13,64 = 0,380, (1 + 189∙193,4/(22,01∙103)] 13,64 = 0,380,A'f= (2133 – 180)  30 = 58590 мм2, 30 = 58590 мм2,µ'f = 58590/(180∙270) = 1,21, Z= 1,21∙30/(2∙270 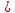 = 0,067, = 0,067,xN= 270 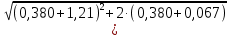 – (0,380+ 1,21)] = 70,2 мм; – (0,380+ 1,21)] = 70,2 мм;Кривизна оси: (1/ρ)2 = (54,6∙103 – 193,4∙189)/[(200000∙10-3∙509∙189(270 – 70,2] = 0,00000472 мм-1. Кривизна оси при продолжительном действии постоянной и временной длительной нагрузок Mp = 22,01 кН∙м: A'f= (2133 – 180)  30 = 58590 мм2; 30 = 58590 мм2;µ'f = 58590/(180∙270) = 1,21; Z= 1,21∙30/(2∙270 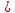 = 0,067; = 0,067;Eb,red = (Rbn/εb1,red) = 22/0,0028 = 7857 МПа, где εb1,red = 0,0028 (табл. 6.10 [4]); αs2 = Es/Eb,red= 200000 (22/0,0028) = 25,46; αs2 = Es/Eb,red= 200000/7857 = 25,46; К = [509/(180∙270)  (1 + 189∙193,4/(22,01∙103)] 25,46 = 0,709. (1 + 189∙193,4/(22,01∙103)] 25,46 = 0,709.xN= 270 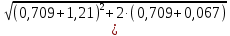 – (0,709 + 1,21)] = 99,9 мм; – (0,709 + 1,21)] = 99,9 мм;(1/ρ)3 = (54,6∙103 – 193,4∙189)/[(200000∙10-3∙509∙189(270 – 99,9] = 0,00000554 мм-1. Полная кривизна оси: (1/ρ) = 588∙10-8 – 472∙10-8 + 554∙10-8 = 670∙10-8 мм-1. Прогиб плиты: f = Sl02 (1/ρ) = (5/48)  58602 58602 0,00000670 = 24 мм < (1/200)5860 = 29,3 мм. 0,00000670 = 24 мм < (1/200)5860 = 29,3 мм.Жесткость плиты обеспечена. Конструкция в целом удовлетворяет требованиям второй группы предельного состояния. Расчет плиты на стадии транспортирования и монтажа. Монтажные петли совмещены с опорными закладными деталями, что делает расчетную схему плиты при монтаже такой же, как и при эксплуатации (однопролетная свободно опертая балка). Прочность заведомо достаточна. Расчетная схема плиты при транспортировании представляет собой двухконсольную балку с опорами в месте первых промежуточных ребер, где располагаются подкладки при транспортировании. Вылеты консолей l1 = 1,015 м. Коэффициент динамичности kd = 1,6 м (п.5.1.6 СП[4]), тогда погонная нагрузка и момент от собственного веса плиты составят: q1 = qsvkd = 1,67∙3  1,6 = 8,02 кН/м. 1,6 = 8,02 кН/м.М = q1l12/2 = 8,02∙1,0152/2 = 4,13 кН∙м Назначим диаметр верхних и нижних стержней, входящих в каркас с поперечными стержнями, диаметром 6 мм с суммарной площадью сечения 56,5 мм2 с каждой стороны. Плита в соответствии с нормами рассчитывается как внецентренно сжатый элемент: Np ep ≤ Rbbx(h0 – 0,5x) + Rsc As'(h0 – as'), где Np = (σsp(1) γsp– 300) A'sp = (465,4∙1,1 – 300)509 = 108103 Н = 108 кН; σsp(1) = 480 – 14,4 = 465,4 МПа – величина предварительного напряжения арматуры с учетом первых потерь; ep – расстояние от точки приложения усилия обжатия с учетом влияния изгибающего момента М от собственного веса элемента до центра тяжести сечения растянутой или наименее сжатой ненапрягаемой арматуры от этих усилий, определяемое по формуле: ep = eop + 0,5h – as± M/Np = 168,5+ 0,5∙300 – 30 – 4,13∙103/108 = 267,8 мм. Уточним значение граничной относительной высоты сжатой зоны ξR = 0,8/(1+ Ɛs,el/Ɛb2) = 0,8/[1 + (435/200000)/0,003] = 0,464, отсюда xR= ξR∙h0= 0,464∙277 = 128 мм. x = (Np + Rs As – Rsc As')/(Rb b) = [(108103 + 435∙56,5 – 330∙56,5)]/(14,5∙170) = 46,2 мм < 128 мм. Rbb x(h0 – 0,5x) + Rsc As'(h0 – as') = 14,5∙180∙46,2(277 – 0,5∙46,2) + 330∙56,5(277 – 30) = 35,22106 Н∙мм = 35,22 кН∙м Np ep = 108∙267,8 = 28922 кН∙мм = 28,92 кН∙м. Прочность обеспечена. Подбор монтажных петель Монтажные петли из арматуры класса А240 марки ВСт3сп2 совмещены с опорными закладными деталями. Из четырех монтажных петель в расчете рассматривают три. Усилие, приходящееся на одну петлю: N= 29,41,4/3 = 13,73 кН, где 29,4 кН – расчетный вес плиты, 1,4 – коэффициент динамичности при монтаже. В соответствии с табл. 5.4 [15] принимаем диаметр 14 мм, который соответствует расчетному усилию не более 15 кН. |
