Расчет подпорной стенки. Расчет подпорной стенки
 Скачать 259.83 Kb. Скачать 259.83 Kb.
|
Расчёт стенки из железобетонаОпределение размеров поперечного сечения консоли. Бетон относится к конструктивным материалам с явно выраженным различием восприятия сжимающих и растягивающих элементов. Поэтому бетонные конструкции рассчитываются только на сжимающие напряжения. Допустимые сжимающие напряжения в бетоне зависят от его класса. На рисунке 13 приведены по [1, 5] значения допустимых напрягающих напряжений на сжатие Rb в зависимости от класса бетона. 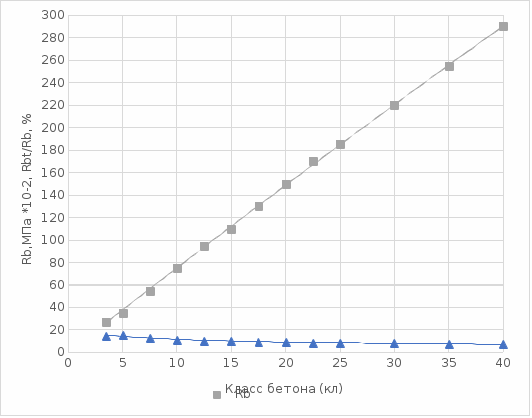 Рис. 13. Зависимости допустимых сжимающих Rпр и относительных растягивающих Rbt/Rb% напряжений в бетоне класса В3,5 –В40 Относительная величина в % растягивающих напряжений от допустимых сжимающих находится в пределах от 16 до 7%. На рисунке 13 приведены графические зависимости и относительных растягивающих Rbt/Rb в % напряжений для бетонов в пределах диапазона значений класса бетона В3,5 – В40. Чисто бетонные конструкции рассчитываются по допустимым напряжениям на сжатие. В случае превышения растягивающих напряжений допустимых, в бетонной конструкции появляются поперечные трещины, которые уменьшают величину поперечного сечения конструкции и его момент сопротивления W. При возникновении такой ситуации, трещины мгновенно распространяются на всё поперечное сечение, приводя к разрушению конструкции. Для предотвращения разрушения бетонной конструкции растягивающими напряжениями, в растянутой зоне устанавливается арматура, которая воспринимает эти растягивающие напряжения. При установке арматуры в растянутой зоне бетона максимальная величина поперечных трещин в бетоне будет ограничиваться величиной упругого растяжения арматуры, которая ограничит раскрытие трещин в бетоне в соответствии с законом Гука: где: еб – величина раскрытия одной трещины в бетоне при появлении растягивающего напряжения σ>Rbt; l – расчётная длина элемента бетонной конструкции; Rs – величина растягивающего усилия в арматуре; Еs – модуль упругости арматуры. Линейный размер бетонной конструкции, на которые будет трескаться бетон при появлении в нём растягивающих усилий, также определится из формулы Гука. При появлении в бетоне растягивающего напряжения Rbt, упругое растяжение величиной еб произойдёт на участке длиной Δl, определяемой по формуле (7): где: еб – величина раскрытия одной трещины в бетоне при появлении растягивающего напряжения σ>Rbt; Δl – расчётная длина сплошного элемента бетонной конструкции; Rb – величина растягивающего усилия в бетоне; Еb – модуль упругости бетона. Максимальная величина упругого растяжения бетона будет: Количество элементов, на которые растрескается растянутый элемент бетонной конструкции, определится соотношением величин полной упругой деформации арматуры и бетона: Модуль упругой деформации бетона зависит от размера заполнителя класса бетона, возраста бетона и его влажности. Зависимость начального модуля деформации Еb=f(класса бетона) для пластичного бетона с заполнителем не более 40 мм от класса бетона приведена на рисунке 14. 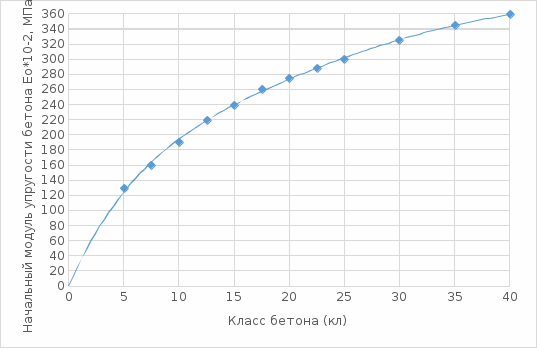 Рис. 14. Зависимости начального модуля деформации бетона класса В5 –В40 Этой зависимостью можно пользоваться при предварительных расчётах бетонных конструкций. При окончательных расчётах следует уточнить расчётное значение модуля деформации для соответствующих параметров бетона. По формуле (10) можно оценить степень раздробленности элемента бетонной конструкции в растянутой зоне. В качестве примера сравним деформации растянутой зоны бетона класса В15 с начальным модулем упругости Еb=24000МПа МПа и Rp=0,75МПа, армированной арматурой класса А500 с нормативным напряжением Rs=435 МПа и модулем упругости арматуры Еs=210000 МПа. По (10) получаем: Для предупреждения растрескивания бетонной конструкции растягивающими напряжениями при армировании арматурой класса А500, необходимо ограничить растягивающие напряжения в арматуре величиной Rа.max=435/66=6,6МПа, что связано с сильным перерасходом дорогостоящей арматуры. Поэтому на ограничение напряжений идут в тех случаях, когда нельзя допускать большие величину раскрытия трещин, например, при размещении железобетонных конструкций в агрессивной для арматуры среде, или из условия недопущения фильтрации через трещины в емкостях для хранения жидкостей и газов. Для определения оптимальных параметров необходимо задаться рядом значений допустимой величины сжимающих напряжений в бетоне и для них по эпюре изгибающих моментов определить толщину стенки по высоте, рассчитать потребную площадь поперечного сечения арматуры, подобрать количество и диаметр стержней арматуры, определить объём бетона и массу арматуры и их стоимость на единицу длины стенки. Эти расчёты следует выполнить для ряда значений класса бетона и после этого построить график зависимости стоимости одного погонного метра подпорной стенки Ц=f(Класс бетона). Минимум этого графика и определит оптимальные параметры подпорной стенки. При оптимизационных расчётах параметров конструкций полезно иметь аналитические зависимости определяемых параметров конструкций от основного определяющего параметра. Однако, в большинстве случаев при таких расчётов получаются дискретные значения, по которым сложно оценить весь диапазон требуемых параметров. В этом случае становится незаменимо графическое представление результатов расчётов с последующей аппроксимацией результатов расчётов. После аппроксимации становится возможным аналитическое исследование результатов расчётов с отысканием экстремальных значений полученных функций и оптимальных значений решаемой задачи. На рисунке 15 приведен график изменения изгибающего момента в консоли подпорной стенки в зависимости от расстояния z сечения от верхней грани консоли M=f(z). Там же приведена аппроксимация зависимости уравнением M = 0,133z3 + 1,5z2. При выполнении расчётов и построении графиков в Excel, аппроксимация выполняется автоматически в различных функциях. Наибольшую гибкость имеет аппроксимация полиномом вида y=ax0+bx1+cx2+…+nx6. Excel позволяет использовать полиномы 6-й степени, чего достаточно, практически, для большинства расчётов. 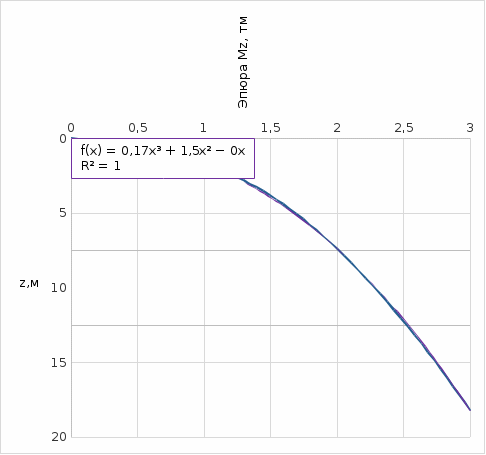 Рис. 15. Зависимость изгибающих моментов от давления грунта и её аппроксимация M=f(z) При установке продольной арматуры в растянутой зоне бетона величина поперечного сечения уже будет определяться величиной сжатых напряжений, которые допускаются в расчётах. Максимальное напряжение в сжатой зоне бетона будет определяться величиной допустимых сжимающих напряжений Rb, которые зависят от класса бетона. Таким образом, при расчёте бетонной неармированной стенки её толщина будет определяться величиной допустимых растягивающих напряжений Rbt, а при армировании площадь поперечного сечения арматуры будет определять величину максимальных сжимающих напряжений [σ], равных призменной прочности бетона Rb. Определение толщины армированного элемента бетонной конструкции выполняется по уравнению (6’), в которое вместо допустимого растягивающего напряжения Rbt подставляется допустимое сжимающее напряжение бетона Rb. На рисунке 16 приведены пунктирными линиями результаты расчётов толщины консоли по высоте в зависимости от класса бетона и их конструктивное оформление по линейному закону при толщине верхней грани tо=0,08м. 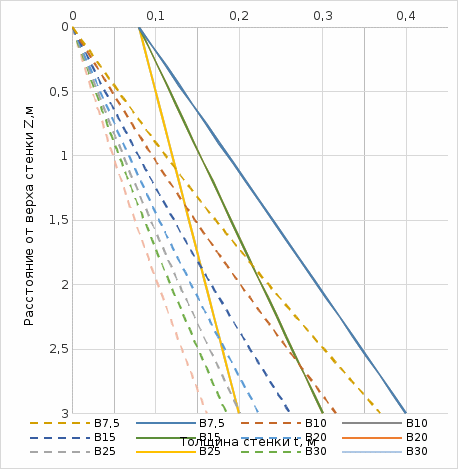 Рис. 16. Изменение толщины стенки по глубине в зависимости от класса бетона t=f(z, кл=const) В таблице 3 приведены результаты расчётов удельных объёма бетона консоли, плиты и всей стенки по призменной прочности бетона с учётом конструктивного оформления толщины для железобетонной подпорной стенки. Таблица 3. Удельные объёмы бетона консоли, плиты и всей стенки для железобетонной подпорной стенки
По данным таблицы 3 на рисунке 17 построены соответствующие графики зависимости объёма бетона на 1 пог. м длины консоли, плиты и суммарный объём стеки. 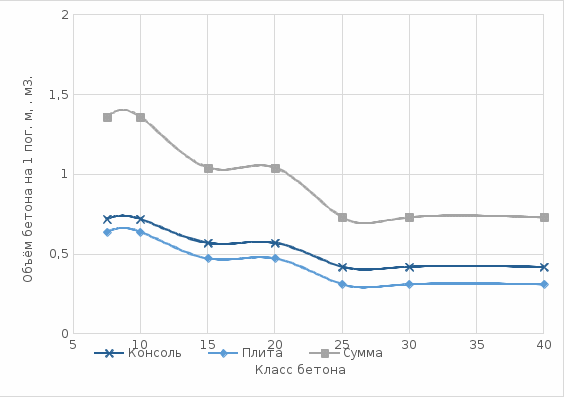 Рис. 17. Графики зависимости объёма бетона на 1 пог. м длины консоли, плиты и суммарный объём стенки. В таблице 4 приведены удельные показатели стоимости бетона консоли подпорной стенки, её плиты и общая стоимость одного погонного метра железобетонной подпорной стенки в зависимости от класса бетона. Таблица 4. Удельные стоимости бетона консоли, плиты и всей стенки из железобетона
По данным таблицы 4 построены графики на рисунке 18 зависимости стоимости бетона в железобетонной конструкции подпорной стенки. 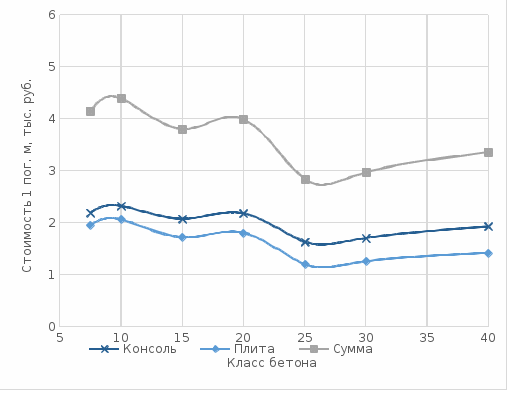 Рис. 18. Графики зависимости стоимости бетона на 1 пог. м длины консоли, плиты и суммарная стоимость бетона ж-б стенки. Расчёт арматуры Расчёт арматуры, устанавливаемой в конструкциях, работающих на изгиб, выполняются из обеспечения следующих условий [1, 2, 3, 4, 5, ]: где mа – коэффициент условий работы арматуры; Rs - нормативное сопротивление арматуры; Fs’ – площадь сжатой арматуры; В настоящих расчётах армирование сжатой зоны бетона не предусматривается, поэтому принимается Fsʹ=0. На рисунке 19 показана расчётная схема распределения усилий в поперечном сечении бетонной стенки при установке рабочей арматуры только в растянутой зоне бетона при изгибе. 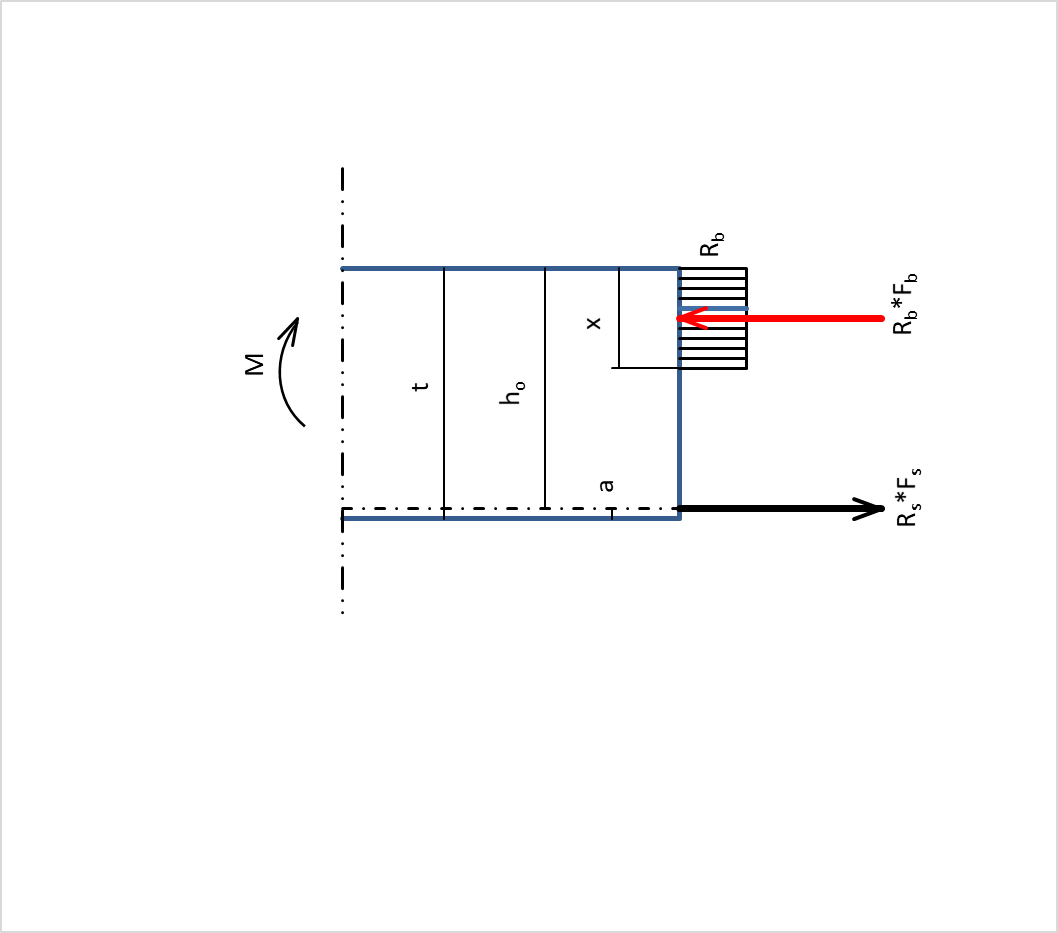 Рис. 19. Схема распределения усилий в поперечном сечении стенки при изгибе На схеме рисунка 15 приняты следующие обозначения: М – изгибающий момент; х – расчётная длина площадки сжатого бетона с учётом релаксации напряжений; Fb – площадь сжатого бетона; Rb – призменная прочность бетона; Rb*Fb – усилие от напряжений сжатия бетона; Fs – площадь поперечного сечения арматуры; Rs – расчётное сопротивление арматуры; Rs*Fs – расчётное усилие в арматуре. t – высота поперечного сечения бетона; hо=t-a – расчётная высота поперечного сечения бетона; a – расстояние от внешней грани бетона до оси поперечного сечения арматуры; Для определения величины площадки х сжатого сечения бетона необходимо воспользоваться вторым принципом Даламбера и составить уравнение равновесия сил относительно т. А, а для определения площади поперечного сечения Fа арматуры составить уравнение равновесия сил относительно т. О. С учётом принятых обозначений условия равновесия сил в поперечном сечении бетона будут иметь вид: - относительно т. А: откуда получаем Сумма нормальных сил по условиям статического равновесия в сечении позволяет определить потребную площадь поперечного сечения арматуры: откуда получаем Принимая в (14) Rb и Rs=435 в МПа и b=100 см, получим расчётную формулу для определения требуемой площади арматуры Fа в см2/пог. м длины подпорной стенки: Результаты расчётов потребного сечения арматуры в поперечных сечениях по высоте консоли подпорной стенки, полученное в результате вычислений по формуле (15), в графическом виде представлено на графиках рисунка 20. В плите подпорной стенки потребуется уложить примерно такое же количество рабочей арматуры. С учётом укладки распределительной и конструктивной арматуры, в первом приближении, примем, что суммарная потребность арматуры составляет 2,5 объёма расчётного количества рабочей арматуры в консоли подпорной стенки. 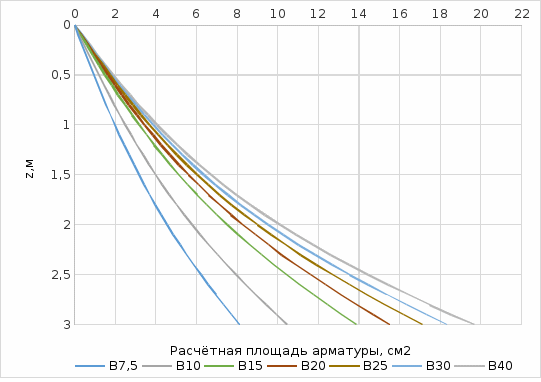 Рис. 20. Расчётное потребное количества арматуры в поперечных сечениях консоли подпорной стенки Расчётный вес потребной арматуры на 1 погонный метр подпорной стенки приведен в таблице 5, в которой так же приведены удельные показатели стоимости бетона и арматуры проектируемой подпорной железобетонной стенки в зависимости от класса бетона. Таблица 5. Удельные стоимости бетона консоли, плиты и всей стенки из железобетона
По данным таблиц 4 и 5 на рисунке 21 построены графики стоимости бетона консоли, опорной плиты подпорной стенки и их сумма, стоимость арматуры и полная удельная стоимость железобетонной подпорной стенки. 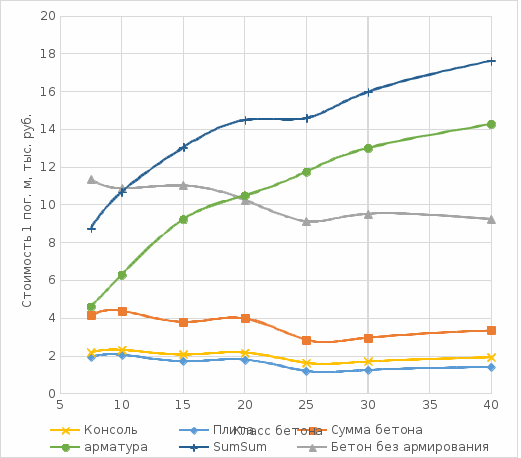 Рис. 21. Расчётное потребное количества арматуры в консоли подпорной стенки Как видно по этим графикам, минимальная стоимость железобетонной подпорной стенки получается при использовании бетона класса В25 и составляет 9,13 тыс. руб./пог. м. Минимальная стоимость бетонной подпорной стенки равна 8,77тыс. руб./пог. м при использовании бетона класса В7,5, что на 4% дороже железобетонной стенки. После выполнения изложенных предварительных расчётов следует выполнить детальные расчёты оптимального варианта подпорной стенки с подбором и раскладкой арматуры для получения окончательных экономических показателей. Список литературыСП 381.1325800.2018 Сооружения подпорные. Правила проектирования. М.: Стандартинформ, 2018. Справочник. Мелиорация и водное хозяйство. Т. 4. Сооружения. М.: ВО Агропромиздат. 1987. – 464 с. Свод правил. Основания зданий и сооружений. Soil bases of buildings and structures. Актуализированная редакция СНиП 2.02.01-83*. ОКС 93.020 Ксенофонтова Т. К., Чумичева М. М. Железобетонные подпорные стенки. Учебное пособие. /Т. К. Ксенофонтова, М. М. Чумичева. /Московский государственный университет природообустройства. М., 2010, 153 с. Чумичёва М. М. Покрытия одноэтажных зданий. Часть 1. Балки. Учебное пособие. М.: Спутник+, 2017. – 53 с. СП 45.13330.2017 Земляные сооружения, основания и фундаменты. Актуализированная редакция СНиП 3.02.01-87 (с Изменениями N 1, 2). Дата начала действия: 28 августа 2017. Дата редакции: 20 ноября 2019. Недрига В. П. Гидротехнические сооружения. Справочник проектировщика /Г. В. Железняков, Ю. А. Ибад-Заде, П. Л. Иванов и др.; Под общ. Ред В. П. Недриги. – М.: Стройиздат, 1983. -544 с. |
