Модуль. Модуль №1 НЭК. Расчет показателей надежности резервированных устройств с учетом восстановления. Теоретические сведения
 Скачать 397.5 Kb. Скачать 397.5 Kb.
|
|
Модуль № 1. Расчет показателей надежности резервированных устройств с учетом восстановления. Теоретические сведения. Резервирование, при котором возможно восстановление отказавших элементов, является эффективным средством повышения надежности. Отказ резервированной группы с восстановлением произойдет, если все элементы, составляющие группу, ремонтируются. При резервировании с восстановлением резерв как бы все время пополняется восстанавливаемыми блоками. Показатели надежности, как правило, определяются при условии, что в момент включения все элементы работоспособны. Наиболее часто используются два метода расчета надежности восстанавливаемых систем, которые условно называются: метод интегральных уравнений и метод дифференциальных уравнений. Будем рассматривать в дальнейшем 2-ой метод. В методе дифференциальных уравнений использовано допущение о показательных распределениях времени между отказами и времени восстановления. Вначале перечисляются возможные состояния системы и составляется ее математическая (логическая) модель в виде схемы состояний, на которой прямоугольниками или кружками изображаются возможные состояния и стрелками - возможные направления переходов из одного состояния в другое. По схеме состояний составляют систему дифференциальных уравнений для вероятностей состояний. Для этого целесообразно использовать следующие правила: левые части уравнений содержат производные по времени вероятностей соответствующих состояний знак зависит от направления стрелки (плюс, если стрелка направлена острием к состоянию, и минус в противном случае); число уравнений равно числу состояний; система дифференциальных уравнений должна быть дополнена нормировочным условием, состоящем в том, что сумма вероятностей всех состояний равна единице. Решение системы дифференциальных уравнений с помощью преобразований Лапласа или каким-либо другим методом позволяет определить требуемые показатели надежности. Когда перерывы в работе системы допустимы, в качестве показателей надежности используют функцию готовности Кг(t) и функцию простоя Kп(t) или коэффициенты готовности Kг и простоя Кп определяемые в виде Функция готовности Kг(t) равна по определению вероятности того, что в момент времени t система исправна. Фунция простоя Кп(t) равна вероятности того, что в момент времени t система неисправна. Имеют место соотношения Кг(t)+Kп(t)=1; (2) Кг+Кп=1. Часто рассматривают установивший режим эксплуатации при t . Тогда Когда перерывы в работе системы недопустимы, в качестве показателей надежности используются условные вероятности непрерывной безотказной работы в течение заданного времени выполнения задачи При нескольких работоспособных состояниях 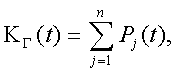 (3) (3)где n число работоспособных состояний; Pj(t) вероятность jго работоспособного состояния. Часто число неработоспособных состояний значительно меньше числа работоспособных. При этом удобнее вычислять коэффициент простоя 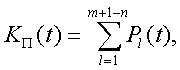 (4) (4)где Pl(t) вероятность lго неработоспособного состояния; m+1 - общее число состояний. Особенности расчета резервированных систем Система, состоящая из равнодежных одного основного и k резервных элементов, может находиться в любом из (k+2) состояний: 0 - все элементы работоспособны; 1 - один элемент в неработоспособном состоянии; j когда j элементов в неработоспособном состоянии; k+1 когда (k+1) элементы в неработоспособном состоянии. Предполагается, что при замене работающего элемента на резервный перерыва в работе системы не происходит, поэтому отказ системы наступает при одновременной неработоспособности основного и всех резервных элементов (состояние k+1). Рассмотрим случай ненагруженного резерва с абсолютно надежным переключателем и с одной ремонтной бригадой, обслуживающей систему (ограниченное восстановление). По предположению, элементы в ненагруженном резерве имеют интенсивность отказов =0. Если число неработоспособных элементов оказывается больше одного, то существует очередь на ремонт. Схема состояний системы представлена на рис. 1. Система дифференциальных уравнений имеет следующий вид: : : : : При t система (5) переходит в систему алгебраических уравнений: P0+P1=0 ; : : Pj1 (+)Pj + Pj+1=0 ; : : Pk Pk+1=0. Для решения системы (6) необходимо добавить уравнение 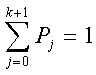 . (7) . (7)В результате решения системы (6) совместно с уравнением (7) получим установившиеся значения коэффициентов простоя и готовности 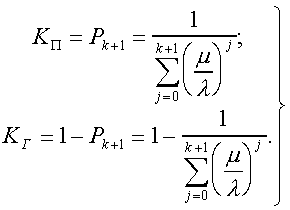 ; (8) ; (8)Если та же система, состоящая из k+1 элементов, обслуживается (k+1) ремонтными бригадами (неограниченное восстановление), то очередь на ремонт отсутствует. Схема состояний для ненагруженного резерва и неограниченного восстановления представлена на рис.2. В результате решения системы уравнений при Pj(t)=0 получим: 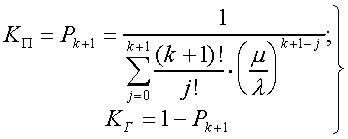 (9) (9)Схемы состояний для системы, состоящей из одного основного и k элементов в нагруженном резерве представлены на рис.3. для ограниченного восстановления и на рис.4. - для неограниченного. Рассуждая аналогично, получим: для ограниченного восстановления 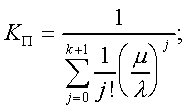 Kг=1Kп ; (10) Kг=1Kп ; (10)для неограниченного восстановления 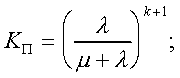 (10a) (10a)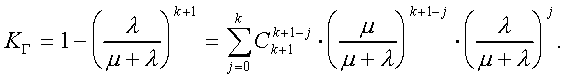 Рассмотрим резервированные системы, для которых отказы недопустимы, но ремонт отказавшего элемента производится во время выполнения задачи. Если система состоит из основного элемента и k элементов в нагруженном резерве, то для случая ограниченного восстановления схема состояний представлена на рис.5. При попадании системы в состояние (k+1) происходит отказ системы, который недопустим и приводит к невыполнению поставленной задачи. Вероятность безотказной системы работы 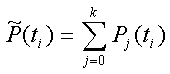 (11) (11)найдена в предположении, что при t=0 в системе нет неиспользованных элементов, т.е. P0(0)=1; P1(0)= ... =Pk+1(0)=0. Вероятность отказа системы в течении времени выполнения задачи также является условной вероятностью и равна Важным показателем является среднее время безотказной работы 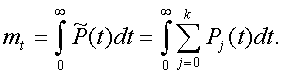 (13) (13)При решении системы уравнений, составленных по схеме состояний рис.5. с помощью преобразований Лапласа, целесообразно использовать правило, облегчающее расчет. Для определения среднего времени безотказной работы достаточно найти преобразование Лапласа вероятности безотказной работы P(s) и подставить в него s=0. Решение типовых задач Задача 1. Для питания радиостанции используется электроагрегат с двумя генераторами, каждый из которых обладает производительностью, достаточной для нормальной работы: эти генераторы работают поочередно. При отказе работающего генератора в работу включается резервный генератор, а отказавший отключается и ремонтируется. Отказ электроагреграта состоит в прекращении питаниия радиостанции. Конструкция электроагрегата допускает одновременный ремонт обоих генераторов, имеется нужное число ремонтников. Интенсивность отказов одного генератора равна , а интенсивность восстановления одного генератора равна . Вычислить коэффициент готовности электроагрегата, если =5. Предполагается показательное распределение времени безотказной работы и времени восстановления. Решение. Электроагрегат может находится в одном из трех состояний, которые обозначены цифрами: 0 - электроагрегат работоспособен, оба генератора работоспособны. 1 - электроагрегат работоспособен, но один из генераторов отказал и находится в ремонте. 2 - электроагрегат неработоспособен, оба генератора ремонтируются. Обозначим вероятности указанных состояний в момент времени t через P0(t), P1(t), P2(t). Эти вероятности при t имеют пределы P0 , P1 , P2 . Поскольку для рассматриваемого электроагрегата переход из состояния 0 в состояние 1 не нарушает его работоспособности, то K=P0+P1 . Составим схему состояний (рис.6.) и соответствующую этой схеме систему уравнений Для определения установившихся значений P0 и P1 положим все производные равными нулю. Учитывая, что P0(t)+P1(t)+P2(t)=1, получаем: P0+P1=0 ; P0(+)P1+2P2=0 ; P0+P1+P2=1 . Для получения величин P0 , P1 , P2 используем правило Крамера: где определитель, элементами которого являются коэффициенты при P0 , P1 , P2 ; i определитель, который образуется из путем замены iго столбца коэффициентами правой части системы уравнений. Определим , 0 , 1 . Имеем 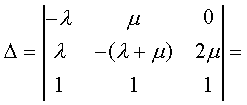 ( + ) + 22 + 2 =2 + 2( + ) . ( + ) + 22 + 2 =2 + 2( + ) .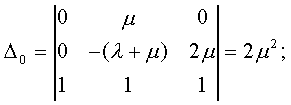 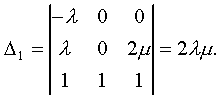 Определим P0 , P1 . Получим 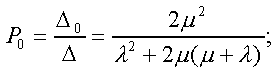 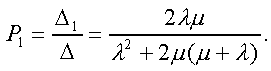 Обозначив 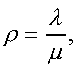 получим в результате Соответственно При =0,2 получим K=0,98 . Задача 2. Связная радиостанция включает в себя приемный и передающий блоки, интенсивности отказов которых одинаковы и равны =102 1/час . Интенсивность восстановления =2 1/час . Станцию обслуживает одна ремонтная бригада. При неработоспособности любого из блоков радиостанция неработоспособна. При этом работоспособный блок не выключается и в нем могут происходить отказы. Требуется определить значения коэффициентов готовности и простоя радиостанции. Решение. Связная радиостанция в любой момент времени может находиться в одной из трех состояний: 0 - оба блока работоспособны; 1 - один блок работоспособен; 2 - оба блока неработоспособны. Радиостанция работоспособна только в состоянии 0 и неработоспособна в состояниях 1 и 2. Схема состояний с соответствующими интенсивностями переходов представлена на рис.7. Этой схеме соответствует система дифференциальных уравнений: При t 2P0 + P1=0 ; 2P0 (+)P1 + P2 = 0 ; P1 P2 = 0 . При решении этой системы используем нормировочное условие P0 + P1 + P2 = 1 , которое может заменить любое из уравнений системы. В результате решения системы уравнений либо подстановкой, либо по правилу Крамера получим 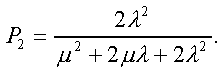 Коэффициент готовности радиостанции равен Коэффициент простоя 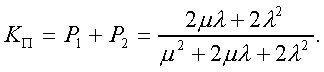 Подставляя числовые значения, получаем: K102; K = 1 K0,99 . Задача 3. Специализированная бортовая ЭВА состоит из трех блоков (1,2 и3), два из которых (1 и 2) включены последовательно в основную цепь, а блок 3 находится в состоянии ненагруженного резерва (рис.8.). Известно также, что интенсивность отказов 2 блока 2 пренебрежимо мала по сравнению с интенсивностями отказов 1 и 3 блоков 1 и 3 (т.е. 1 = 3 >> 2) и устройство эксплуатируется в условиях ограниченного восстановления. Требуется определить коэффициенты готовности K и простоя K . Интенсивность отказов и восстановлений устройства равны соответственно и , причем = . Решение. Если предположить, что наличие в системе блока 2 не ухудшает ее надежность, то можно выделить следующие три состояния, в которых может пребывать устройство: 0 - блоки 1 и 3 исправны и ЭВА работоспособна; 1 - один из блоков (1 или 3) поврежден и ремонтируется, а система по-прежнему сохраняет работоспособность; 2 - оба блока (1 и 3), а следовательно, и система в целом неработоспособна. Схема перечисленных состояний приведена на рис.9. Обозначим вероятности указанных состояний в некоторый момент времени t соответственно P0(t) , P1(t) , P2(t) . Очевидно, что Ясно, что K= P0 + P1 , поскольку переход системы из состояния 0 в состояние 1 (0 1 ) не отражается на ее работоспособности, а K = P2 или K = 1 K , так как P0 + P1 + P2 = 1 . Запишем уравнения, соответствующие схеме состояний устройства. В соответствии с (5) и рис.9. получим Дополнив систему уравнений нормировочным условием (7), при t имеем P0 + P1 = 0 , P0 ( + )P1 + P2 = 0 , P1 P2 = 0 , P0 + P1 + P2 = 1 . Совместное решение 1-го, 2го и 4-го уравнений системы дает следующий результат 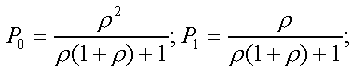 где Поскольку = / = 1 по условиям задачи, то, подставив это значение в формулы вероятностей состояний системы, получим P0 = P1 = P2 = 0,3333, поэтому K = P0 + P1 = 0,6666 , K = P2 = 1 K = 0,3333 Задача 4. Преобразователь “параметр-код” состоит из рабочего блока и блока в ненагруженном резерве. Распределения времен между отказами и восстановления показательные с параметрами= 8103 1/час , = 0,8 1/час . Требуется определить значения коэффициентов простоя и во сколько раз уменьшается величина коэффициента простоя преобразователя при применении неограниченного восстановления по сравнению с ограниченным. Решение. Для определения значений коэффициентов простоя для случаев ограниченного и неограниченного восстановления воспользуемся соответственно выражениями (8) и (9). Число возможных состояний равно трем. Для ограниченного восстановления 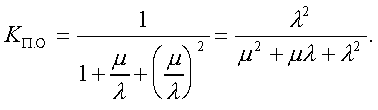 Для неограниченного восстановления 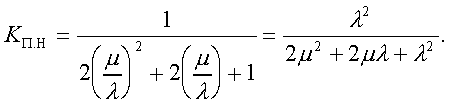 Для рассматриваемой задачи справедливо соотношение >> , и полученные выражения могут быть с достаточной для практики точностью определены приближенно: Таким образом, при применении неограниченного восстановления по сравнению с ограниченным величина коэффициента простоя уменьшилась в два раза. Значения этих коэффициентов равны: K. 104 ; K. 0,5*104 . Задача 5. Радиоприемное устройство, состоящее из рабочего блока и блока в нагруженном резерве, рассчитано на непрерывную круглосуточную работу. Через три часа после включения это устройство может получить команду на перестройку режима работы. Интенсивность отказов и восстановления каждого блока равны= 8103 1/час ; = 0,2 1/час . Имеются две дежурные ремонтные бригады. Определить вероятность застать радиоприемное устройство в неработоспособном состоянии через три часа после включения (значение функции простоя) и значение коэффициента простоя. Решение. Радиоприемное устройство в любой момент времени может находиться в одном из следующих состояний: 0 - оба блока работоспособны; 1 - один блок неработоспособен; 2 - оба блока неработоспособны; При нахождении в состояниях 0 и 1 устройство работоспособно, в состоянии 2 - устройство неработоспособно. Схема состояний устройства с соответствующими интенсивностями переходов представлена на рис.10. Система дифференциальных уравнений, составленная по этой схеме, имеет вид Для определения функции простоя решим эту систему при начальных условиях P0(0) = 1 ; P1(0) = P2(0) = 0 . Переходя к изображениям, получаем систему алгебраических уравнений: (s + 2)P0(s) P1(s) = 1 ; 2P0(s) + (s + + )P1(s) 2P2(s) = 0 ; P1(s) + (s + 2)P2(s) = 0 . Для получения величин Pi(s) используем правило Крамера где определитель, элементами которого являются коэффициенты при P0(s) , P1(s) , P2(s) ; i определитель, который образуется из путем замены iго столбца коэффициентами правой части системы. В рассматриваемом случае требуется определить функцию простоя, равную P2(t) . Для этого запишем определители и 2 : 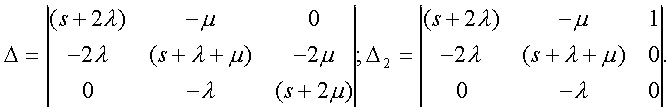 Следовательно 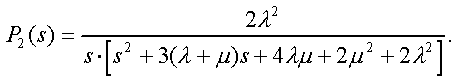 Найдем корни уравнения s2 + 3( + )s + 2( + )2 = 0 . Имеем =0,53( + ) Следовательно, s1 = 2( + ) ; s2 = ( + ) . Запишем P2(s) в виде 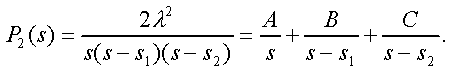 Определим A , B , C . Имеем 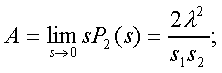 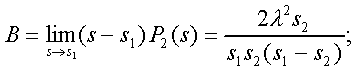 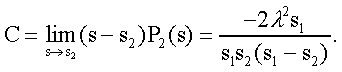 Производя обратное преобразование Лапласа P2(t) = L1{P2(s)} , получим: P2(t) = A1(t) + 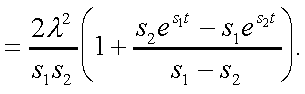 Так как 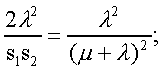 s1 s2 = -( + ) , s1 s2 = -( + ) ,то 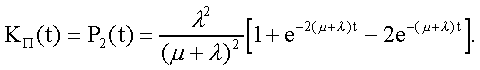 Используя это выражение, определяем коэффициент простоя при t 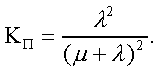 Подставляя числовые значения, получаем K (3)= 2104 ; K = 1,5103 . Задача 6. Вычислительное устройство состоит из рабочего блока и блока в ненагруженном резерве. Интенсивность отказов и восстановлений каждого блока равны = 2*102 1/час ; = 2 1/час . При одновременной неисправности обоих блоков устройство неработоспособно. Определить среднее время безотказной работы устройства mt . Решение. Вычислительное устройство в любой момент времени может находиться в одном из следующих состояний: 0 - оба блока работоспособны; 1 - один блок неработоспособен; 2 - оба блока неработоспособны. Схема состояний устройства представлена на рис.11. Для определения mt сначала необходимо определить вероятность непрерывной безотказной работы в течении времени t . Система дифференциальных уравнений, полученная по схеме состояний, имеет следующий вид: Начальные условия: P0(0) = 1 ; P1(0) = P2(0) = 0 . При помощи преобразования Лапласа получаем систему алгебраических уравнений относительно изображений: (s+)P0(s) P1(s) = 1 ; P0(s) + (s + + )P1(s) = 0 ; P1(s) + sP2(s) = 0 . Путем решения этой системы либо подстановкой, либо по правилу Крамера получим 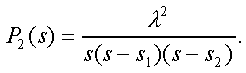 Раскладывая P2(s) на элементарные дроби и производя обратное преобразование Лапласа, определяем вероятность P2(t) попадания за время (0 , t) в состояние 2 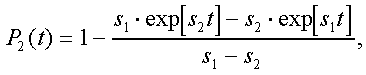 где обозначено Следовательно, вероятность непрерывной безотказной работы вычислительного устройства за время (0 , t) равна 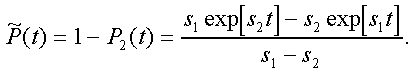 Среднее время безотказной работы mt равно 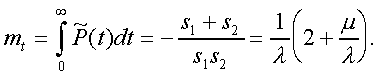 Задача 7. Радиолокационная станция сопровождения содержит рабочий блок и блок в нагруженном резерве. Интенсивность отказов и восстановлений каждого блока равны соответственно и . Время сопровождения в среднем составляет величину tc . При одновременной неработоспособности обоих блоков сопровождаемая цель теряется и происходит отказ станции. При переходе на резервный блок потери цели не происходит. Требуется определить вероятность непрерывной безотказной работы в течение времени (0 , tc), или, иначе, вероятность непопадания в состоянии 2 на этом интервале и среднее время безотказной работы станции mt . Решение. Радиолокационная станция сопровождения в любой момент времени может находиться в одном из следующих состояний: 0 - оба блока работоспособны; 1 - один блок неработоспособен; 2 - оба блока неработоспособны. Схема состояний представлена на рис.12. Работоспособными являются состояния 0 и 1, неработоспособным - 2. Следовательно, вероятность непопадания в состояние 2 за время tc определяется как Для определения вероятности При помощи преобразования Лапласа получаем систему алгебраических уравнений относительно изображений при P0(0) = 1 ; P1(0) = P2(0) = 0 : (s + 2)P0(s) P1(s) = 1 ; 2P0(s) + (s + + )P1(s) = 0 ; P1(s) + sP2(s) = 0 . Путем решения этой системы либо подстановкой, либо по правилу Крамера, получим: 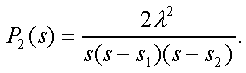 Раскладывая P2(s) на элементарные дроби и производя обратное преобразование Лапласа, определяем вероятность попадания в состояние 2 за время (0 , tc ): 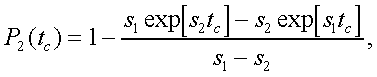 где обозначено Следовательно, вероятность непрерывной безотказной работы радиолокационной станции за время (0 , tc) равна: Для определения среднего времени безотказной работы станции mtзапишем преобразование Лапласа для вероятности безотказной работы P(s) и подставим в него s = 0 : 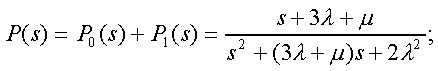 Задача 8. Станция радиорелейной связи включает два работающих приемопередающих блока и один блок в ненагруженном резерве. Наработка на отказ каждого работающего блока mt=200 час ; среднее время восстановления одного блока m=2 час . Станцию обслуживает одна ремонтная бригада. При неработоспособности двух блоков станции третий блок выключается и в нем не могут происходить отказы. Требуется определить коэффициент простоя станции. Решение. Возможны следующие состояния радиорелейной связи: 0 - все блоки работоспособны; 1 - неработоспособен один блок; 2 - неработоспособны два блока. При неработоспособности одного блока блок из ненагруженного резерва переводится в рабочее состояние. Работоспособными являются состояния 0 и 1, неработоспособным - состояние 2. Обозначим вероятности указанных состояний в момент времени t через P0(t) , P1(t) , P2(t) . Эти вероятности при t имеют пределы P0 , P1 , P2 . В рассматриваемом случае K= P2 , т.к. состояние 2 является неработоспособным. Составим схему состояний (рис.13.) и соответствующую этой схеме систему уравнений Для определения установившегося значения P2положим все производные равными нулю. Учитывая, что P0(t) + P1(t) + P2(t) =1 , получаем 2P0 + P1 = 0 ; 2P0 ( + 2)P1 + P2 = 0 ; P0 + P1 + P2 = 1 . Для получения величины P2 используем правило Крамера: 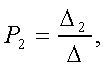 где 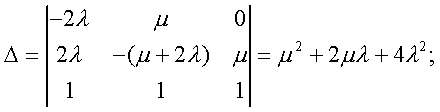 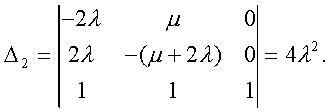 Следовательно 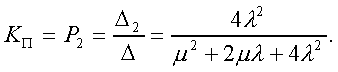 при >> 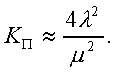 Так как при показательном распределении времени безотказной работы и времени восстановления то Задачи для самостоятельного решения. Задача 1. Радиорелейная станция содержит два приемопередатчика, один из которых используется по назначению, а второй находится в ненагруженном резерве. Определить среднее время безотказной работы станции mt при условии, что для каждого приемопередатчика 2*103 1/час ; 0,2 1/час . Задача 2. Регистрирующее устройство содержит рабочий блок и блок в нагруженном резерве. Вероятность отказа блока в течение 25 часов q(ti) 0,1 . Ремонт производится одной бригадой с интенсивностью0,21/час . Определить коэффициент простоя регистрирующего устройства. Задача 3. Система связи содержит одно устройство, предназначенное для выполнения задачи и одно устройство в нагруженном резерве. Интенсивность отказов каждого устройства равна1/час , восстановления 1/час. Ремонт устройств производится независимо друг от друга. Определить функцию готовности. Задача 4. Система сопровождения состоит из рабочего блока и блока в нагруженном резерве. Для каждого блока заданы:2*103 1/час , 0,2 1/час . Определить время безотказной работы системы. Задача 5. Преобразователь “параметр-код” состоит из рабочего блока и блока в нагруженном резерве. Распределения времен между отказами и восстановления показательные с параметрами 8*1031/час , 0,8 1/час. Требуется определить значения коэффициентов простоя и во сколько раз уменьшается величина коэффициента простоя преобразователя при применении неограниченного восстановления по сравнению с ограниченным. Задача 6. Устройство состоит из двух одинаковых блоков, один из которых использутся по прямому назначению, а второй находится в нагруженном резерве. Интенсивность отказов каждого блока 6*103 1/час , интенсивность восстановления 2 1/ час. Ремонт производится одной ремонтной бригадой. Требуется определить коэффициент простоя устройства. Задача 7. Усилитель состоит из двух равнонадежных блоков, для каждого из которых 3*103 1/час . Имеется усилитель в ненагруженном резерве. Ремонт производит одна бригада, среднее время ремонтаm = 0,5 час . Определить коэффициент простоя усилителя с резервом. Задача 8. Усилитель состоит из двух равнонадежных блоков, для каждого из которых3*103 1/час . Применено поблочное резервирование усилителя в ненагруженном режиме. Ремонт производит одна бригада, среднее время ремонтаm = 0,5 час . Определить коэффициент простоя усилителя с поблочным резервированием. Задача 9. Вычислитель состоит из двух одинаково рабочих блоков и одного блока в нагруженном скользящем резерве. Для каждого блока 8*103 1/час ; 1 1/час , ремонтных бригад две. Определить коэффициент простоя вычислителя. Задача 10. Вычислитель состоит из двух одинаковых рабочих блоков и одного резервного блока в ненагруженном резерве. Для каждого блока 8*103 1/час ; 1 1/час , ремонтных бригад две. Определить коэффициент простоя вычислителя. Задача 11. Генератор импульсов содержит один рабочий блок, один блок в нагруженном резерве и один блок в ненагруженном резерве. При неработоспособности рабочего блока или блока в нагруженном резерве блок из ненагруженного резерва переводится в нагруженный. Задано для каждого блока 102 1/час, 0,5 1/час , ремонтная бригада одна . Определить коэффициент простоя генератора. Задача 12. Передатчик содержит рабочий блок (9*103 1/час ) и блок в облегченном резерве (103 1/час ). Определить коэффициент простоя передатчика при условии, что ремонт производится одной бригадой с интенсивностью0,3 1/час . Задача 13.Преобразователь частоты содержит один рабочий блок и один блок в нагруженном резерве. Ремонт производится одной бригадой, обеспечивающей среднее время восстановления0,5 час. Определить предельно допустимую интенсивность отказов преобразователя, чтобы удовлетворялось условиеK 2*104 . Задача 14. Преобразователь частоты содержит один рабочий блок и один блок в ненагруженном резерве. Ремонт производится одной бригадой, обеспечивающей среднее время восстановления 0,5 час. Определить предельно допустимую интенсивность отказов преобразователя, чтобы удовлетворялось условиеK 2*104 . Задача 15. Для нерезервированного изделия, имеющего интенсивность отказов 2*102 1/час , может быть применен либо нагруженный, либо ненагруженный резерв. Ремонт производится одной ремонтной бригадой с интенсивностью 2 1/час . Определить, во сколько раз уменьшится значение коэффициента простоя при применении ненагруженного резерва вместо нагруженного. 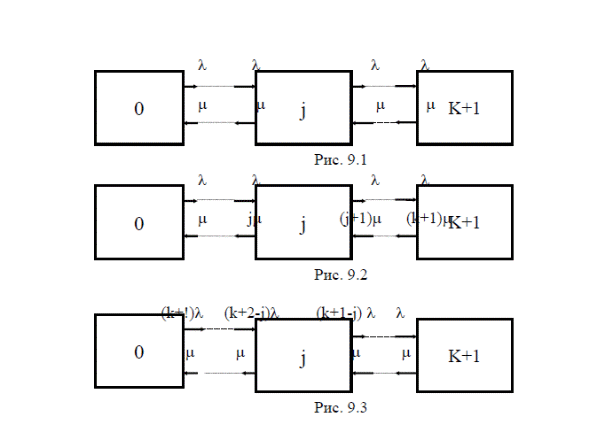 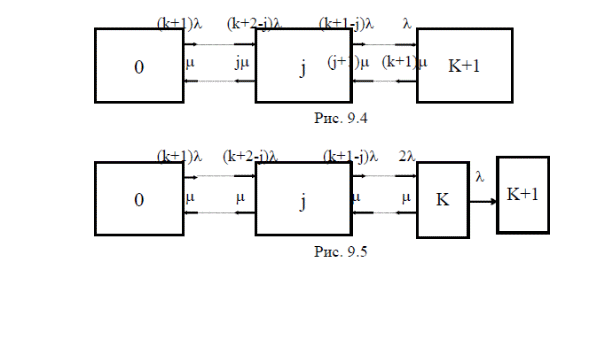 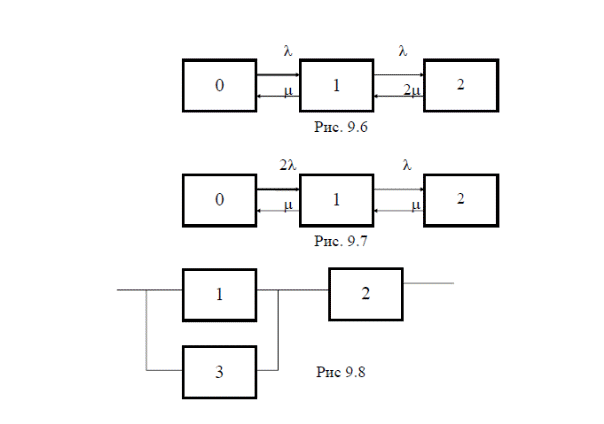 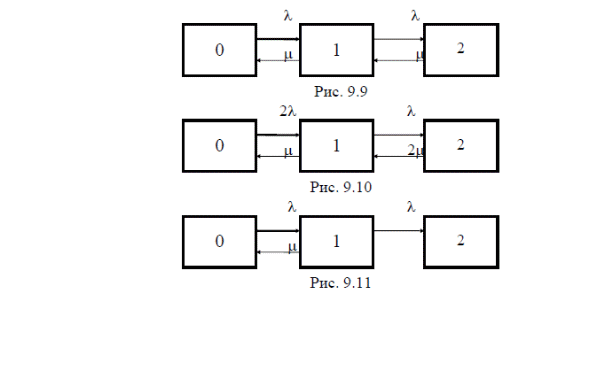 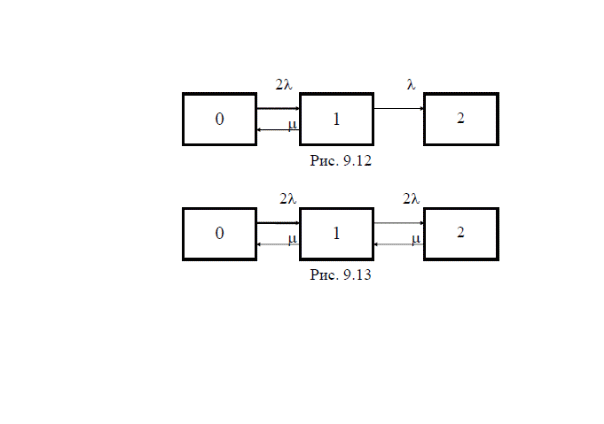 |
