работа 2 ПАВ Евсеенко А.Д. озб-2н92н. Расчёт процесса вытеснения нефти с помощью пав
 Скачать 58.77 Kb. Скачать 58.77 Kb.
|
|
Расчёт процесса вытеснения нефти с помощью ПАВ. В водонасыщенный участок пласта шириной b = 390 м, толщиной h = 14 м, пористостью т – 0,25 и с расстоянием между нагнетательной и добывающей галереями l 490 м через нагнетательную галерею закачивается водный раствор ПАВ с концентрацией с0 и темпом закачки q 480 м3/сут. ПАВ сорбируется скелетом породы по закону Генри, формула которого имеет вид: a(c) ac , где – коэффициент сорбции; 0,2. Определить скорость продвижения фронта сорбции ПАВ (фронта ПАВ) и построить график распределения концентрации ПАВ в пласте в произвольный момент времени. Решение. Для определения скорости фронта ПАВ и распределения их концентрации в пласте выведем уравнение материального баланса. Для этого выделим элемент объёма пласта (рис. 1) V xbh , в котором будем считать движение жидкостей, происходящим вдоль оси Ох, и составим уравнение баланса объёма ПАВ. Воду и водный раствор ПАВ будем считать несжимаемыми жидкостями. 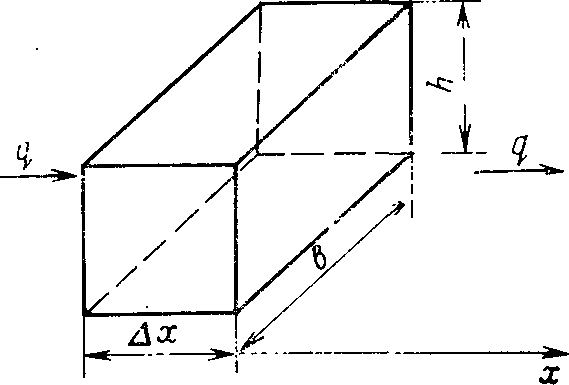 Рисунок 1 – Элемент прямолинейного пласта За время t в элемент V войдёт объём ПАВ: Q1 qпавt qc(x,t)t. За то время из элемента V выйдет объём ПАВ: Q2 qпавt qc(x x,t)t .   В момент времени t в элементе объёма пласта AV было ПАВ: Q3 mV[c(x,t) (x,t)] . За время t количество ПАВ изменилось и стало равным:   Q4 mV[c(x,t t) (x,t t)]. Здесь x – некоторая точка интервала x , в которой концентрация ПАВ равна среднему значению концентрации в элементе объёма V в моменты времени t и t t. Составляя уравнение баланса, получим Q1 Q2 Q4 Q3 , соответственно или     qc x,tt qc x x,tt mV[cx,t t x,t t cx,t x,t]. qc x,tt qc x x,tt mV[cx,t t x,t t cx,t x,t].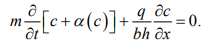 Вспоминая, что по условию задачи a(c) ac , и производя несложные преобразования, получим окончательную форму уравнения баланса водного раствора ПАВ в первоначально водонасыщенном пласте: 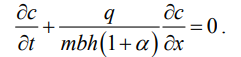 Для решения этого уравнения необходимо знать начальные и граничные условия. Сформулируем эти условия. В начальный момент времени t 0 в пласте отсутствует ПАВ, т. е. c x,0 0 . закачивается водный раствор ПАВ с концентрацией закачки c c . Таким образом, граничное условие будет иметь вид: C 0,t c0 .  Решение вышеуказанных задач хорошо известно, результат определяют по формулам: Решение вышеуказанных задач хорошо известно, результат определяют по формулам:c x,t c0, x q t, mbh1 c x,t 0, xq t. mbh1 Отсюда следует, что фронт сорбции ПАВ движется со скоростью: 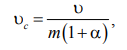 где – линейная скорость фильтрации, 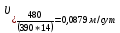 (1.1) (1.1)Подставляя в выражение для скорости фронта сорбции ПАВ значение скорости фильтрации и заданные по условию задачи значения пористости и коэффициента сорбции ПАВ, находим с: с 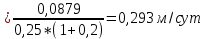 (1.2) (1.2)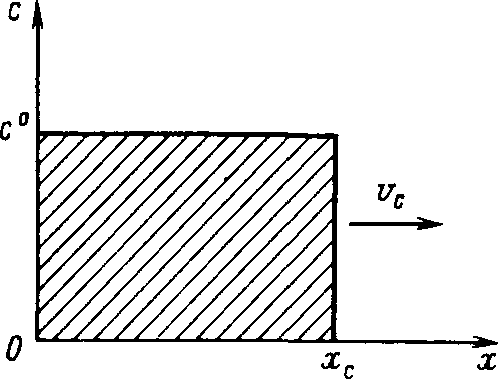 Распределение концентрации ПАВ в пласте вдоль оси Ох в произвольный момент времени t имеет вид, изображенный на рисунке 2. Распределение концентрации ПАВ в пласте вдоль оси Ох в произвольный момент времени t имеет вид, изображенный на рисунке 2.Рисунок 2 – Зависимость концентрации ПАВ в случае линейной изотермы сорбции ПАВ пористой средой от расстояния |
