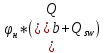Курсовая работа. КР Конструкции. Расчёт ребристой плиты покрытия
 Скачать 125.14 Kb. Скачать 125.14 Kb.
|
|
Расчёт продольного ребра плиты по сечениям, нормальным к продольной оси. Бетон В30 : 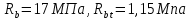 Продольная арматура А800 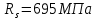 Поперечная арматура В500 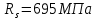 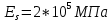  Рис. 1.8. Расчётная схема продольного ребра Защитный слой принимаем а=30 мм, тогда рабочая высота сечения 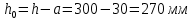 Расчёт производится предполагая, что нейтральная ось проходит в полке, при этом  Так как ширина плиты 2980 мм, принимаем 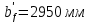 , с учётом граней в 15 мм, b= 150 мм- объединяем два ребра по 75 мм в одну стенку. , с учётом граней в 15 мм, b= 150 мм- объединяем два ребра по 75 мм в одну стенку.Модуль упругости арматуры: 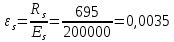 Начальный модуль упругости бетона:  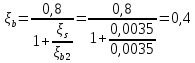 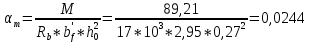 По величине  определяем относительную высоту сжатой зоны бетона: определяем относительную высоту сжатой зоны бетона: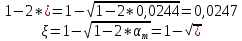 Эту величину сравниваем с высотой предельно сжатой зоны бетона: 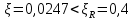 Т.к. условие выполняется, то сжатая арматура не требуется. Величина сжатой зоны: 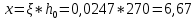 Т.к. 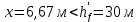 , то нейтральная ось проходит в полке. , то нейтральная ось проходит в полке.Вычисляем относительное плечо внутренней пары сил: 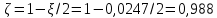 Требуемая по расчёту площадь будет равна: 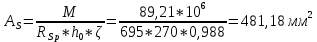 Принимаем поперечную арматуру 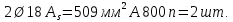 Проверяем несущую способность плиты 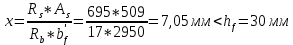 Предельный изгибающий момент: 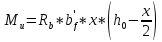 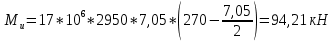 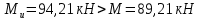 Расчёт продольного ребра плиты по сечениям, наклонным к продольной оси. Расчёт по наклонной сжатой полосе. Рабочая высота сечения: 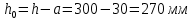 Поперечная сила в нормальном сечении элемента: 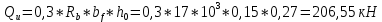 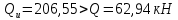 Прочность обеспечена. Расчёт по наклонной трещине. Формулы для расчёта параметров, приведённых в табличной форме для разных значений С.  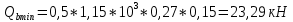 Т.к. 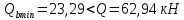 , то требуется поперечная арматура. , то требуется поперечная арматура. 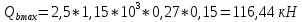 Т.к. 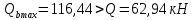 , то размеры поперечного сечения достаточны. , то размеры поперечного сечения достаточны.Принимаем поперечную арматуру 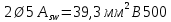 с шагом с шагомS=100 мм,  , , 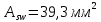 Вычислим погонное усилие, воспринимаемое поперечной арматурой (интенсивность хомутов) Усилие в поперечной арматуре на единицу длины элемента: 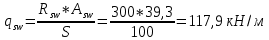 Проверка: 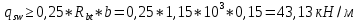 Момент, воспринимаемый бетоном у вершины наклонной трещины:  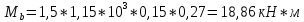 Формулы для расчёта параметров, приведённых в табличной форме для разных значений С (  ) )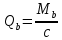 - поперечная сила, воспринимаемая бетоном в наклонном сечении, где с- длина проекции наклонной трещины на продольную ось. - поперечная сила, воспринимаемая бетоном в наклонном сечении, где с- длина проекции наклонной трещины на продольную ось. - поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении. - поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении.  - расчётная поперечная сила у вершины наклонной трещины. - расчётная поперечная сила у вершины наклонной трещины.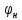 -коэффициент, учитывающий предварительное напряжение арматуры в плите. -коэффициент, учитывающий предварительное напряжение арматуры в плите.Таблица 1.2. Параметры расчёта по наклонной трещине.
 -для каждого с выполняется. -для каждого с выполняется.Все проверки выполнены успешно, прочность конструкции обеспечена. Величину предварительного напряжения продольной арматуры принимаем 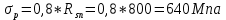 Условно считаем потери напряжения 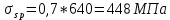 Усилия обжатия плиты: 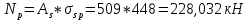 Площадь поперечного сечения плиты: 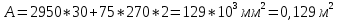 Среднее напряжение обжатия плиты: 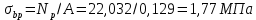 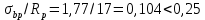 следовательно 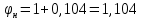 Расчёт продольного ребра плиты по образованию трещин. Продольное ребро плиты длиной 5980 мм запроектировано из тяжёлого бетона В30 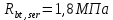 , , 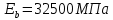 . Продольная напрягаемая арматура . Продольная напрягаемая арматура 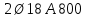 , , 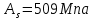 , n= 2 штуки , , n= 2 штуки , 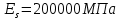 . .Величина изгибающего момента от нормативных нагрузок 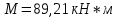 Рис.1.10 Расчётная схема сечения продольного ребра плиты Расчёт ведём для таврового сечения 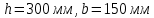 , расчётная ширина полки , расчётная ширина полки 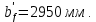 Определяем коэффициент приведения площади арматуры к бетону: 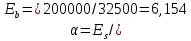 Определяем площадь приведенного сечения: 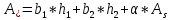 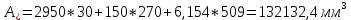 Определяем высоту центра тяжести сечения без учёта арматуры: 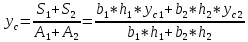 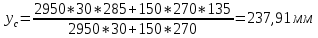 Определяем статический момент сопротивления сечения: 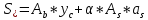 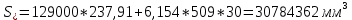 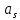 – расстояние от нижней растянутой грани до центра тяжести растянутой арматуры. – расстояние от нижней растянутой грани до центра тяжести растянутой арматуры.Определяем координаты центра тяжести приведённого сечения: 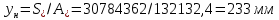 Определим момент инерции сечения без учёта арматуры относительно оси, проходящей через центр тяжести: 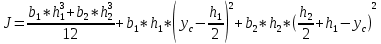 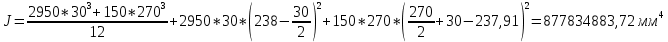 Определяем момент инерции приведённого сечения относительно оси, проходящей через центр тяжести: 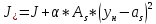 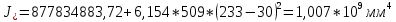 Определяем упругий момент сопротивления приведённого сечения: 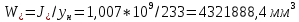 Определяем упругопластический момент сопротивления сечения: 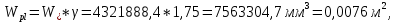 где 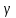 - коэффициент, зависящий от формы сечения - коэффициент, зависящий от формы сечения Определяем момент, воспринимаемый сечением при образовании нормальных трещин: 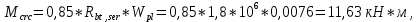 что значительно меньше изгибающего момента от действия полных нормативных нагрузок Условие 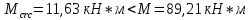 не выполняется, конструкция балки относится к третьей категории трещиностойкости в виду образования нормальных трещин. Необходимо выполнить расчёт по ширине раскрытия нормальных трещин. не выполняется, конструкция балки относится к третьей категории трещиностойкости в виду образования нормальных трещин. Необходимо выполнить расчёт по ширине раскрытия нормальных трещин.Расчёт продольного ребра плиты по ширине раскрытия нормальных трещин. Определяем коэффициент армирования сечения растянутой арматурой: 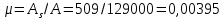 Деформации в растянутой арматуре: 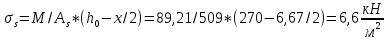 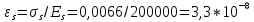 Определяем коэффициент, учитывающий влияние длительности действия нагрузки: 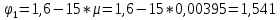 Определяем ширину раскрытия трещины: 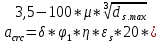 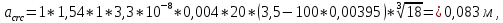 где 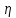 - коэффициент, учитывающий вид арматуры, равный 1,0- при стержневой арматуре периодического профиля, - коэффициент, учитывающий вид арматуры, равный 1,0- при стержневой арматуре периодического профиля,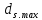 - максимальный диаметр арматуры в растянутой зоне сечения, - максимальный диаметр арматуры в растянутой зоне сечения,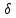 - коэффициент, принимаемый равным 1 – для изгибаемых элементов. - коэффициент, принимаемый равным 1 – для изгибаемых элементов.Расчёт прогибов продольного ребра плиты. Прогиб определяется от постоянной и длительной нагрузок, предельный прогиб 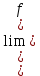 Полный прогиб на участке без трещин в растянутой зоне: 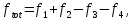 где каждый прогиб вычисляется по формуле: 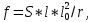 в котором в котором 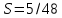 - при равномерно распределённой нагрузке, а кривизна - при равномерно распределённой нагрузке, а кривизна 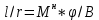 Определяем жёсткость балки: 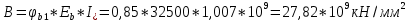 где 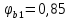 (для тяжёлого бетона)- коэффициент, учитывающий снижение жёсткости сечения вследствие кратковременной ползучести бетона. (для тяжёлого бетона)- коэффициент, учитывающий снижение жёсткости сечения вследствие кратковременной ползучести бетона.Изгибающий момент в середине ребра от нагрузки - полной нормативной: 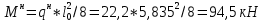 - постоянной и длительной нормативной: 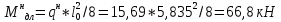 -кратковременной нормативной: 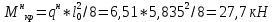 Кривизна и прогиб от кратковременной нагрузки: 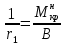 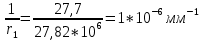 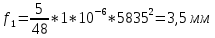 Кривизна и прогиб от постоянной и длительной нагрузок (при 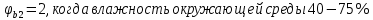 ) )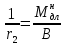 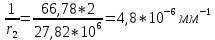 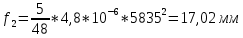 Кривизна и прогиб, вызываемые усилием обжатия 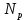 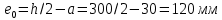 -эксцентриситет действия -эксцентриситет действия 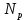 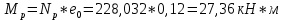 - момент обжатия, - момент обжатия,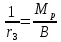 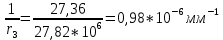 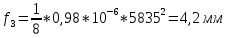 Кривизна и прогиб от ползучести и усадки бетона при отсутствии напрягаемой арматуры в верхней зоне 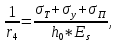 где 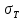 -потери от быстронатекающей ползучести для бетона, подвергнутого тепловой обработке, -потери от быстронатекающей ползучести для бетона, подвергнутого тепловой обработке,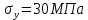 -потери напряжения от усадки бетона, -потери напряжения от усадки бетона,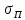 - потери напряжения от ползучести бетона. - потери напряжения от ползучести бетона. 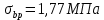 - среднее напряжение обжатия плиты, - среднее напряжение обжатия плиты,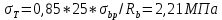 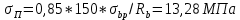 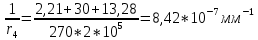 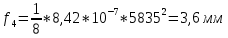 Полный прогиб составит: 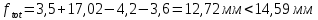 |