Курсовая работа по Механике жидкости и газов. Расчёт системы смазки врд курсовая работа по курсу "Гидрогазодинамика" Вариант 21, задание
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
 . .2.9 Расчёт гидростатического и динамического давления Самый нижний участок отмечен на схеме (рис.1) осью “0-0”. От этой плоскости отсчитаем высоту z и определим значения гидростатического давления 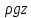 , а также , а также 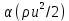 для входа и выхода каждого гидравлического элемента (от бака до форсунки). для входа и выхода каждого гидравлического элемента (от бака до форсунки).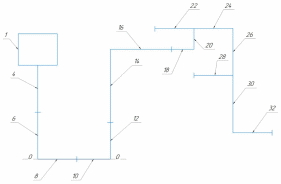 Рисунок 1 – расчетная схема в масштабе по длинам Масляный бак 1: 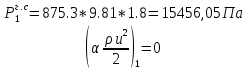 Вход в трубопровод 2: 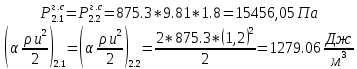 Насос подкачки 3: 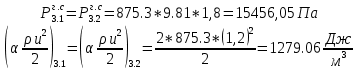 Трубопровод 4: 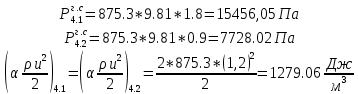 Запорный кран 5: 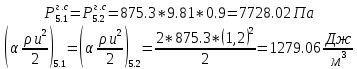 Трубопровод 6: 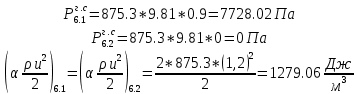 Отвод 7: 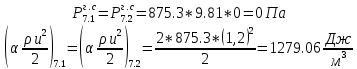 Трубопровод 8: 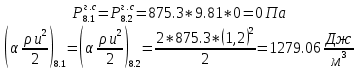 Фильтр 9: 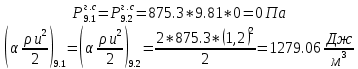 Трубопровод 10: 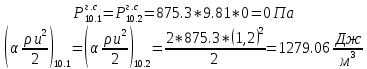 Датчик наличия стружки 11: 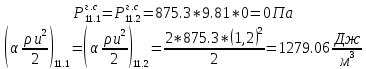 Трубопровод 12: 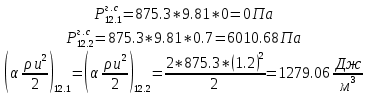 Насос 13: 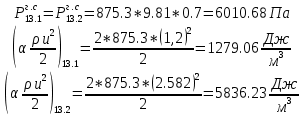 Трубопровод 14: 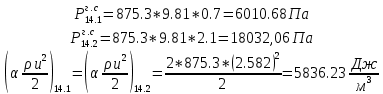 Отвод 15: 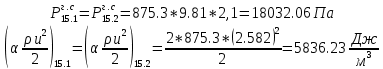 Трубопровод 16: 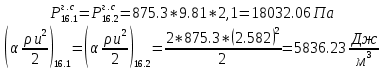 Фильтр 17: 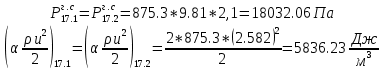 Трубопровод 18: 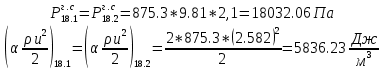 Отвод 19: 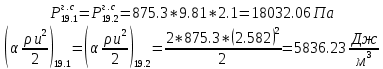 Трубопровод 20: 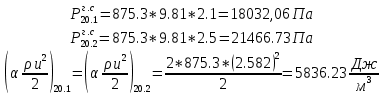 Тройник 21: 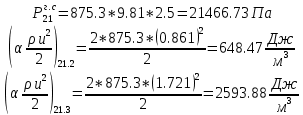 Трубопровод 22: 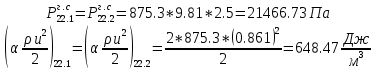 Трубопровод 24: 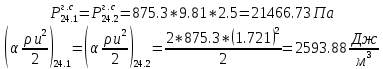 Колено 25: 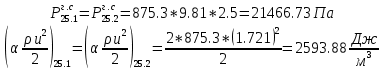 Трубопровод 26: 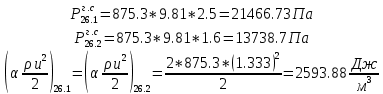 Тройник 27: 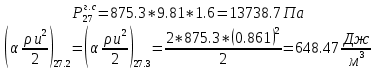 Трубопровод 28: 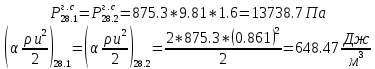 Трубопровод 30: 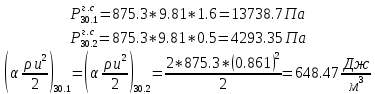 Колено 31: 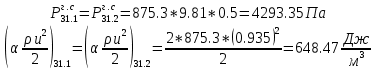 Трубопровод 32: 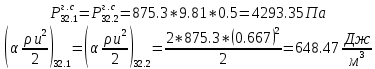 2.10 Определение путевых потерь давления Для начала определим коэффициент Дарси 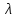 для каждого трубопровода по формуле (5): для каждого трубопровода по формуле (5):Трубопроводы 4-12: 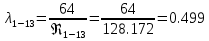 Трубопроводы 14-20: 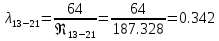 Трубопровод 22: 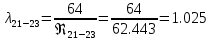 Трубопроводы 24, 26: 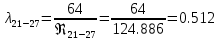 Трубопроводы 28-32: 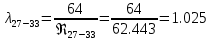 Теперь определим путевые потери каждого трубопровода по формуле (3): Трубопровод 4,6: 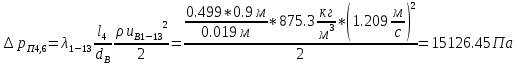 Трубопровод 8 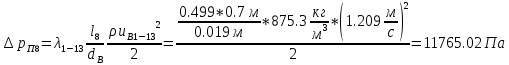 Трубопровод 10: 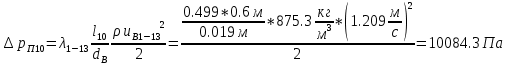 Трубопровод 12: 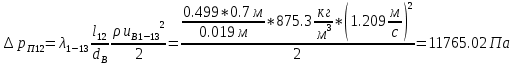 Трубопровод 14: 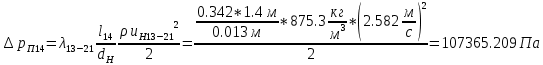 Трубопровод 16: 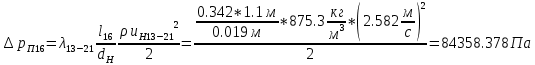 Трубопровод 18,20: 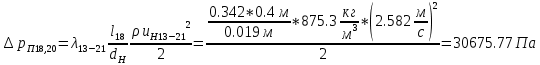 Трубопровод 22: 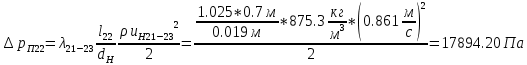 Трубопровод 24: 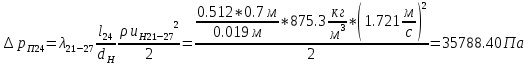 Трубопровод 26: 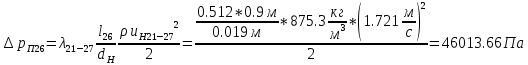 Трубопровод 28,32: 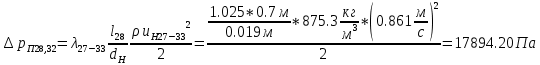 Трубопровод 30: 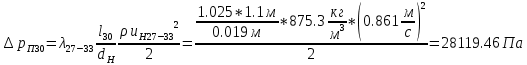 2.11 Определение местных потерь давления Вход в трубопровод 2: Является частным случаем входа в прямую трубу постоянного поперечного сечения: вход в трубу, заделанную в стенку на конечном расстоянии. По заданию дано, что 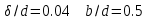 По таблице №3 коэффициент местного сопротивления 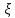 равен из работы [5]: равен из работы [5]: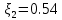 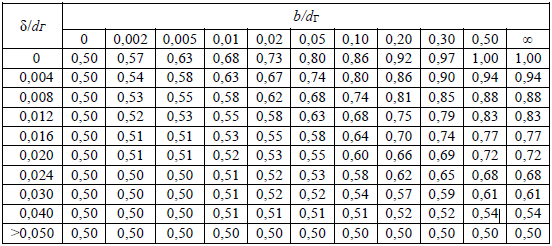 Вычислим местную потерю давления по формуле (2): 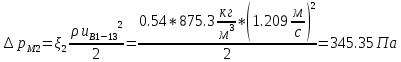 Запорный кран 5: Д  ано по заданию: 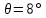 Так как в таблице из работы [5] нет значения 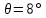 , то воспользуемся методом интерполяции, о котором упомянули и использовали ещё в начале работы. , то воспользуемся методом интерполяции, о котором упомянули и использовали ещё в начале работы.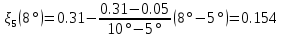 Вычислим местную потерю давления по формуле (12): 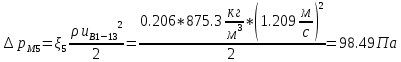 Отвод 7,15: Дано: 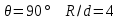 Отводы 7,15 являются отводами плавно изогнутыми (гладкие стенки) при 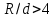 , находящимися за прямым участком трубопровода. , находящимися за прямым участком трубопровода.Коэффициент местного сопротивления в данном случае вычисляется по формуле из работы [5]: 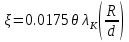 , (14) , (14)где 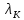 – коэффициент путевых потерь, определяемый по таблице – коэффициент путевых потерь, определяемый по таблице 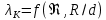 . .Вычислим число Рейнольдса для каждого отвода по формуле (4): 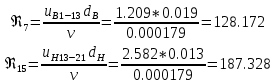 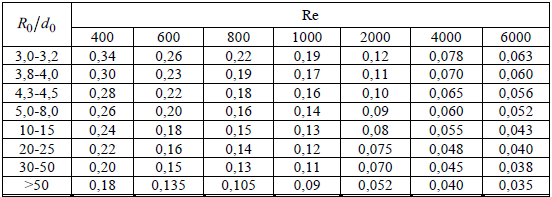 Сверяясь с таблицей №5, примем следующие значения коэффициента путевых потерь 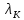 : :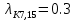 Тогда по формуле (14) коэффициент местного сопротивления будет равен: 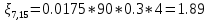 Вычислим местные потери давления для отводов 7,15 по формуле (2): 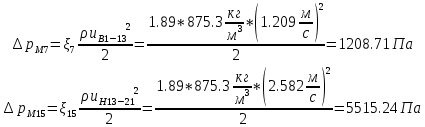 Фильтр 9: Дано: 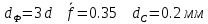 Расчёт фильтра сводится к определению трёх местных потерь давления: при внезапном расширении, при течении жидкости через металлическую сетку и при внезапном сужении. 1. Внезапное расширение (работа [5]). Местное сопротивление в таком случае определяется по формуле: 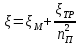 (15) (15)Ввиду малости коэффициента 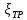 в данной работе им можно пренебречь. в данной работе им можно пренебречь.Так как число Рейнольдса 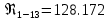 и и 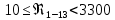 , то для нахождения , то для нахождения 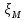 воспользуемся таблицей №6, применяя метод интерполяции, зная при этом, что воспользуемся таблицей №6, применяя метод интерполяции, зная при этом, что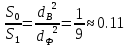 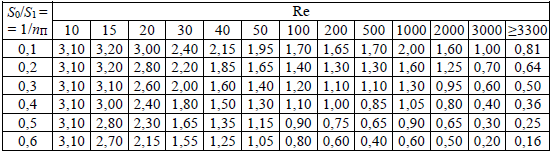 Получаем: 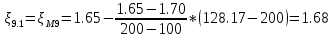 Тогда местная потеря давления по формуле (2): 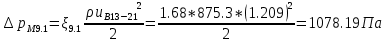 2. Течение жидкости через металлическую сетку (работа [5]). Для начала найдём скорость 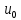 в живом сечении сетки (скорость течения между прутьями сетки), которую можно найти по формуле: в живом сечении сетки (скорость течения между прутьями сетки), которую можно найти по формуле: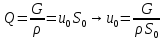 , (16) , (16)где 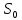 находится по формуле: находится по формуле: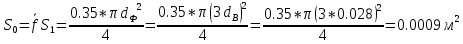 , (17) , (17)где 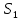 – площадь поперечного сечения до сетки (в широкой части фильтра), – площадь поперечного сечения до сетки (в широкой части фильтра), 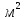 . .Откуда по формуле (16): 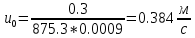 Для определения коэффициента местного сопротивления на участке сетки необходимо знать число 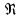 , которое рассчитывается по формуле (4): , которое рассчитывается по формуле (4):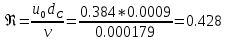 При 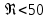 местное сопротивление примерно равно: местное сопротивление примерно равно: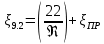 (18) (18)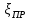 рассчитывается по формуле: рассчитывается по формуле: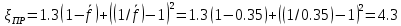 (19) (19)Откуда 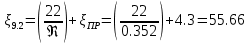 Для определения местной потери давление так же необходимо рассчитать скорость 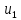 перед сеткой по формуле (16): перед сеткой по формуле (16):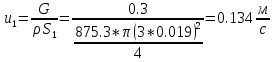 Тогда местная потеря давления по формуле (2): 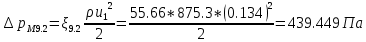 3. Внезапное сужение (работа [5]) Местное сопротивление в таком случае определяется по формуле: 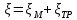 (20) (20)Ввиду малости коэффициента 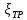 в данной работе им можно пренебречь. в данной работе им можно пренебречь. Так как 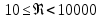 , то значение местного сопротивления , то значение местного сопротивления 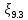 найдём по таблице. ( найдём по таблице. ( 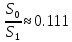 ) )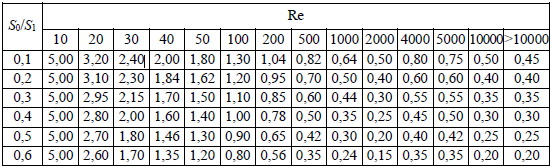 Согласно таблице (работа [5]): 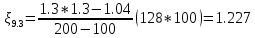 Тогда местная потеря давления по формуле (2): 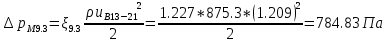 Общая местная потеря давления фильтра 9: 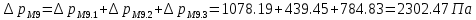 Датчик наличия стружки 11: Дано: 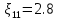 Тогда местная потеря давления по формуле (2): 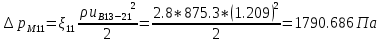 Фильтр 17: Дано: 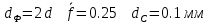 Фильтр 17 рассчитаем по алгоритму, использованному при расчёте фильтра 9. 1. Внезапное расширение. Так как число Рейнольдса 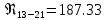 и и 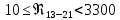 , то для нахождения , то для нахождения 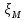 воспользуемся таблицей №6, зная при этом, что воспользуемся таблицей №6, зная при этом, что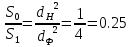 Так как при 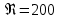 и и 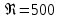 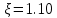 , то и: , то и: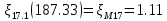 Тогда местная потеря давления по формуле (12): 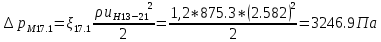 2. Течение жидкости через металлическую сетку. Для начала найдём скорость 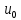 в живом сечении сетки (скорость течения между прутьями сетки), которую можно найти по формуле: в живом сечении сетки (скорость течения между прутьями сетки), которую можно найти по формуле: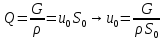 , , где 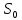 находится по формуле: находится по формуле: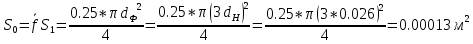 , ,где 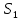 – площадь поперечного сечения до сетки (в широкой части фильтра), – площадь поперечного сечения до сетки (в широкой части фильтра), 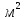 . .Откуда по формуле (15): 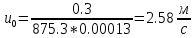 Для определения коэффициента местного сопротивления на участке сетки необходимо знать число 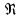 , которое рассчитывается по формуле (4): , которое рассчитывается по формуле (4):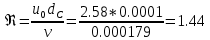 При 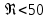 местное сопротивление примерно равно: местное сопротивление примерно равно: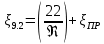 (21) (21)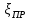 рассчитывается по формуле: рассчитывается по формуле: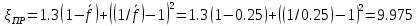 Откуда 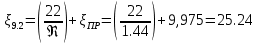 Для определения местной потери давление так же необходимо рассчитать скорость 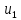 перед сеткой по формуле (15): перед сеткой по формуле (15):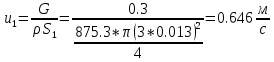 Тогда местная потеря давления по формуле (12): 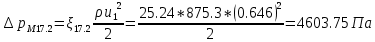 3. Внезапное сужение Рассчитаем число Рейнольдса течения в широкой части фильтра по формуле (4): 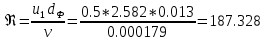 Так как 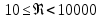 , то значение местного сопротивления , то значение местного сопротивления 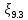 найдём по таблице (работа [5]). ( найдём по таблице (работа [5]). ( 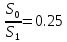 ) )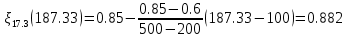 Тогда местная потеря давления по формуле (12): 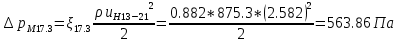 Общая местная потеря давления фильтра 9: 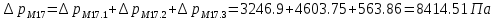 Отвод 19: Дано: 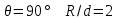 Отвод 19 являются отводом плавно изогнутыми (гладкие стенки) при 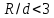 , находящимся за прямым участком трубопровода. , находящимся за прямым участком трубопровода.Коэффициент местного сопротивления на участке отвода находится по формуле (работа [5]): 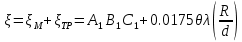 (22) (22)При 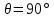 коэффициент коэффициент 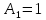 . .П  ри 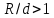 коэффициент коэффициент 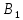 возьмём из таблицы. возьмём из таблицы.Откуда 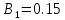 Коэффициент 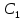 для круглой трубы: для круглой трубы: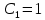 Д  ля нахождения 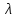 – коэффициента путевых потерь, необходимо вычислить число – коэффициента путевых потерь, необходимо вычислить число 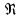 , которое будет равно: , которое будет равно: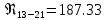 Сверяясь с таблицей (работа [5]), примем значение 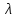 равным: равным: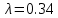 Вычислим местное сопротивление по формуле (17): 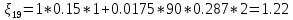 Тогда местная потеря давления по формуле (12): 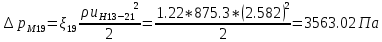 Тройник 21: Тройник 21 является тройником на разделение потока симметричной формы (равносторонний) с резким поворотом на угол 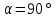 . .Местное сопротивление в таком случае вычисляется по формуле (23) из работы [5]: 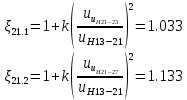 , (23) , (23)где индекс 21.1 означает местное сопротивление левого ответвления; индекс 21.2 – правого ответвления. Тогда местная потеря давления по формуле (2): 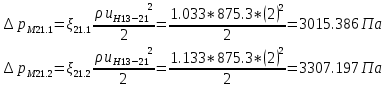 Колено 25,31: Дано:  Колено 25,31 является коленом с острыми кромками в месте поворота (гладкие стенки), находящееся за прямым участком трубопровода. Местное сопротивление в таком случае находится по формуле (24) из работы [5]: 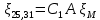 (24) (24)Для круглой трубы коэффициент 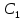 равен: равен: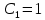 Коэффициент 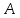 равен из таблицы: равен из таблицы: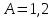 Местное сопротивление 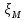 вычисляется по формуле (25) из работы [5]: вычисляется по формуле (25) из работы [5]: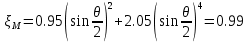 (25) (25)Местное сопротивление по формуле (24): 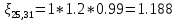 Вычислим местную потерю давления по формуле (2): 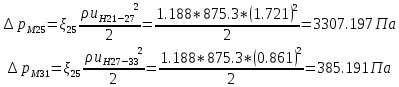 Тройник 27: Дано: 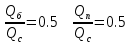 Тройник 27 является тройником приточным с углом поворота 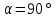 на боковое ответвление. на боковое ответвление.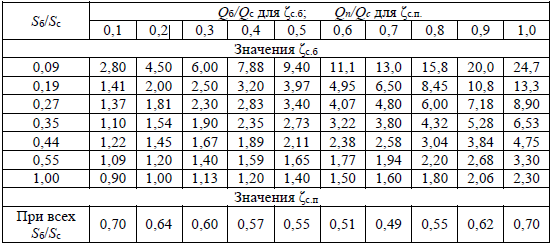 По таблице №10, учитывая, что сечения тройника одинаковы во всех направлениях, примем: 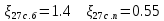 Вычислим местную потерю давления по формуле (2): 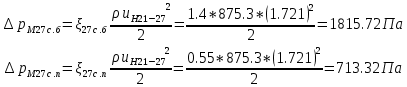
2.12 Давление во входном патрубке насоса Давление во входном патрубке насоса 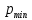 задают равным для смазочной системы: задают равным для смазочной системы: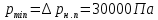 , (26) , (26)где 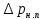 – антикавитационный запас. – антикавитационный запас.2.13 Распределение статического давления во всасывающей магистрали Расчёт ведём от насоса против течения жидкости, последовательно рассматривая все гидравлические элементы. При расчёте используем уравнение Бернулли, учитывая расположение элемента и скорость жидкости на его входе и выходе. Трубопровод 12: 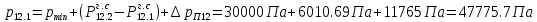 Датчик наличия стружки 11: 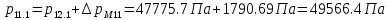 Трубопровод 10: 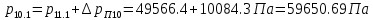 Фильтр 9: 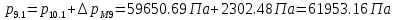 Трубопровод 8: 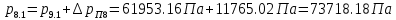 Отвод 7: 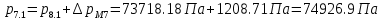 Трубопровод 6: 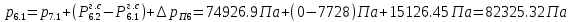 Запорный кран 5: 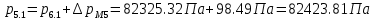 Трубопровод 4: 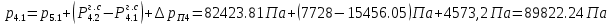 Насос 3: 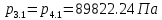 Вход в трубопровод 2: 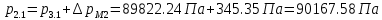 Масляный бак 1: 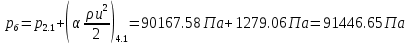 2.14 Сравнение давления в баке с атмосферным давлением на высоте полёта После расчёта распределения давления во всасывающей магистралей становится известным давление в баке 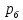 , при котором давление на входе в насос равно заданной величине , при котором давление на входе в насос равно заданной величине 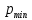 . .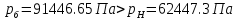 Эту разницу следует обеспечить постановкой подкачивающего насоса непосредственно за баком. Таким образом, перепад давления на подкачивающем насосе: 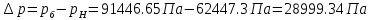 (27) (27)Откуда 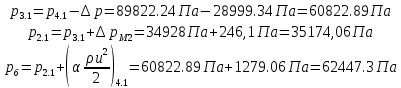 2.15 Нахождение давления на выходе из напорной магистрали Для системы смазки – это давление в среде, окружающей узел опоры: 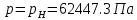 2.16 Определение базовой форсунки Для определения базовой форсунки рассчитаем перепады давлений между общим для всех форсунок сечением системы и сечением перед каждой форсункой. Общим сечением удобно считать сечение перед первым приточным тройником системы 21 (выход из трубопровода 20). При расчёте используем уравнение Бернулли. В качестве базовой выбирается та форсунка, перепад давления до которой от общего сечения системы будет больше. 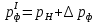 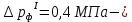 по заданию. по заданию.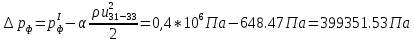 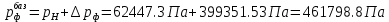 Форсунка 23 базовой быть не может, так как находится слишком близко к тройнику 21, что даёт понять, что она имеет наименьший перепад давлений. Если принять форсунку 29 за базовую: 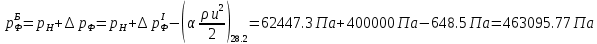 Трубопровод 28: 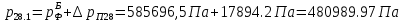 Тройник 27: 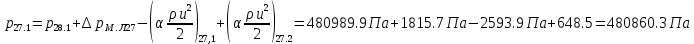 Трубопровод 26: 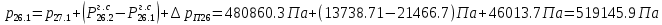 Колено 25: 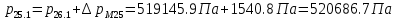 Трубопровод 24: 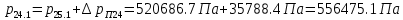 Тройник 21: 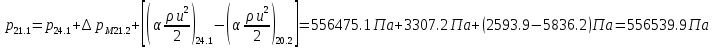 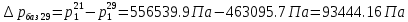 Если принять форсунку 33 за базовую: 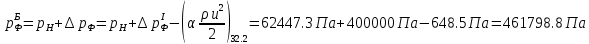 Трубопровод 32: 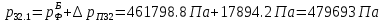 Колено 31: 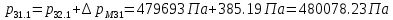 Трубопровод 30: 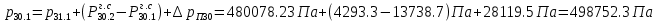 Тройник 27: 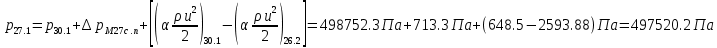 Трубопровод 26: 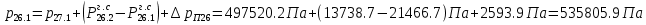 Колено 25: 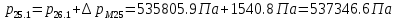 Трубопровод 24: 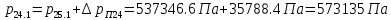 Тройник 21: 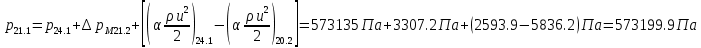 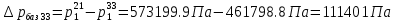 Наибольшим является перепад давлений, если выбрать базовой форсунку под номером 31, следовательно, она является базовой. 2.17 Распределение статического давления в напорной магистрали Расчёт проведём от базовой форсунки к насосу против течения жидкости, последовательно рассматривая все гидравлические элементы. Как и при расчёте всасывающей магистрали, используем уравнение Бернулли, учитывая расположение элемента и величины его скорости на входе и выходе. Давление перед отверстием базовой форсунки (на входе в форсунку) определяется по формуле: 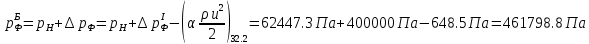 Трубопровод 32: 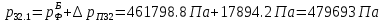 Колено 31: 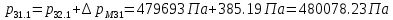 Трубопровод 30: 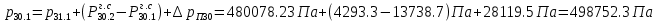 Тройник 27: 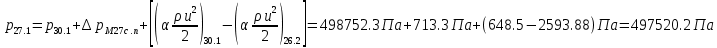 Трубопровод 26: 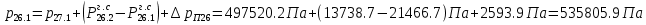 Колено 25: 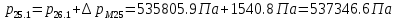 Трубопровод 24: 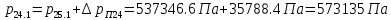 Тройник 21: 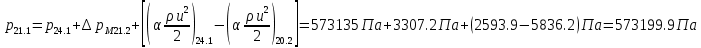 Трубопровод 20: 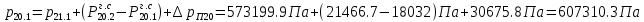 Отвод 19: 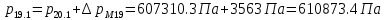 Трубопровод 18: 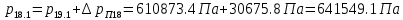 Фильтр 17: 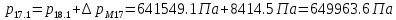 Трубопровод 16: 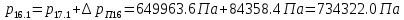 Отвод 15: 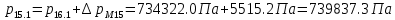 Трубопровод 14: 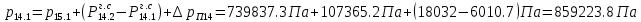 2.18 Расчёт струйной форсунки Расчёт форсунки сводится к определению диаметра отверстия форсунки, при этом мы считаем, что все форсунки данной системы имеют одинаковую геометрию и размеры. Рассчитаем критическое давление по формуле: 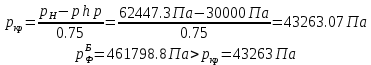 (28) (28)Так как критическое давление больше, то рассчитываем отрывное истечение из отверстия в тонкой стенке при несовершенном сжатии. Определим скорость истечения идеальной (невязкой) жидкости 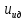 из отверстия форсунки по формуле: из отверстия форсунки по формуле: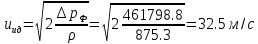 (29) (29)Рассчитаем по формуле отверстие форсунки для идеальной жидкости: 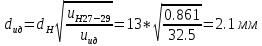 (30) (30)Вычислим число Рейнольдса по теоретической скорости потока в отверстии форсунки: 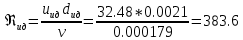 Вычислим соотношение площадей трубопровода и отверстия: 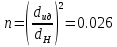 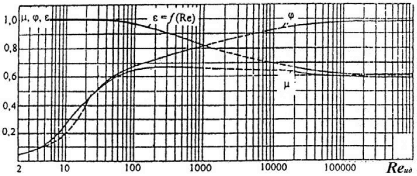 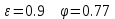 Вычислим коэффициент сужения струи 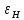 для истечения из отверстия в тонкой стенке при несовершенном сжатии: для истечения из отверстия в тонкой стенке при несовершенном сжатии: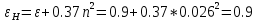 (31) (31)Вычисляют коэффициент расхода 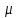 : :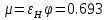 Вычислим площадь отверстия для реального истечения: 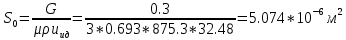 Откуда диаметр отверстия форсунки равен: 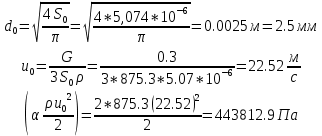 2.19 Вычисление перепада давления на насосе 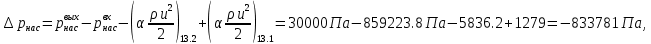 где 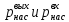 – давления на выходе и входе в насос соответственно. – давления на выходе и входе в насос соответственно.2.20 Расчёт дополнительных гидравлических сопротивлений Форсунка 29: 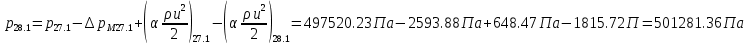 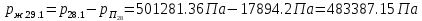 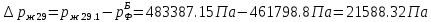 Форсунка 23: 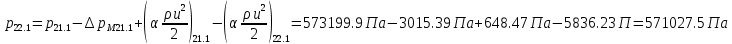 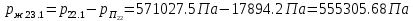 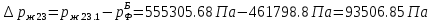 Местные потери в форсунке: 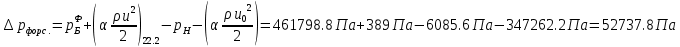 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

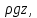 Па
Па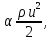
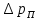 , Па
, Па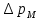 , Па
, Па