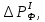Курсовая работа по Механике жидкости и газов. Расчёт системы смазки врд курсовая работа по курсу "Гидрогазодинамика" Вариант 21, задание
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
 11ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ 11ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ“КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н. ТУПОЛЕВА” Кафедра РДиЭУ РАСЧЁТ СИСТЕМЫ СМАЗКИ ВРД Курсовая работа по курсу “Гидрогазодинамика” Вариант №21, задание № Выполнил студент гр. 1342: Шепельский В.М. Принял: Александр Ю.Б. КАЗАНЬ 2021 г.  State educational institution of higher education State educational institution of higher education“Kazan National Research Technical University named by A.N. Tupolev” Calculation of lubrication system Coursework for the course “Hydrodynamics” Variant №21, task № Completed by student of gr.1342: Shepelskiy V.M. Accepted by: Aleksandrov Y.B. Kazan 2020 year СодержаниеАннотация 4 Задание 6 Введение 7 1. Основные понятия и расчётные формулы 8 2. Расчёт гидравлической системы 12 3. Итоговая таблица 47 4. Графическая часть 49 СПИСОК ЛИТЕРАТУРЫ 51  Аннотация Гидравлическая система представляет собой набор гидравлических элементов, которые соединены в определенном порядке, обусловленном назначением и пространственным расположением системы. Гидравлическими элементами являются трубопроводы, баки, насосы, всевозможные виды местных сопротивлений. Обычно система имеет гидравлические элементы, предназначенные для хранения жидкости (баки), передачи жидкости на расстояние (трубопроводы), очистки жидкости (фильтры), управления потоком жидкости (краны, вентили, клапаны, заслонки, термостаты), измерений (расходомеры различных типов), изменения направления или разделения потока жидкости (колена, отводы, тройники, коллекторы), изменения скорости потока жидкости (сужения, расширения), поддержания постоянного уровня жидкости (поплавковые камеры), дозирования и организации истечения жидкости (жиклеры, форсунки, распылители). Гидравлические системы бывают разомкнутыми или замкнутыми (циркуляционными). Система может иметь или не иметь насос (разомкнутая самотечная и замкнутая термосифонная система). Магистраль, по которой жидкость поступает к насосу, называется всасывающей, а магистраль, по которой жидкость движется от насоса, – нагнетающей или напорной. Annotation The hydraulic system is a set of hydraulic elements that are connected in a certain order, depending on the purpose and spatial arrangement of the system. The hydraulic elements are pipelines, tanks, pumps, all kinds of local resistances. Typically, the system has hydraulic elements designed for storing liquid (tanks), transferring liquid over a distance (pipelines), cleaning liquid (filters), controlling the flow of liquid (taps, valves, valves, dampers, thermostats), measurements (flow meters of various types ), changes in the direction or separation of the liquid flow (elbows, bends, tees, collectors), changes in the flow rate of the liquid (contraction, expansion), maintaining a constant liquid level (float chambers), dosing and organizing the flow of liquid (nozzles, nozzles, sprayers ). Hydraulic systems are open or closed (circulation). The system may or may not have a pump (open loop gravity and closed thermosyphon system). The line through which the liquid enters the pump is called the suction line, and the line along which the liquid moves from the pump is called the pressure line or the pressure line. 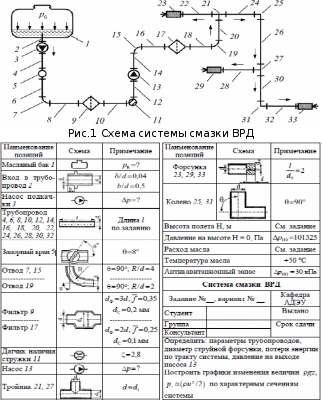 Задание
Введение Система смазки ВРД (рис. 7) предназначена для смазки и охлаждения подшипников опор роторов, зубчатых колес редукторов, приводов, шлицевых соединений рессор, элементов соединительных муфт и т.д. Масло из бака 1 подается насосом 13 к узлам опор, расположенных в разных местах двигателя. К подшипникам масло подводится струйными форсунками 23, 29, 33. Особенностью системы является то, что масло обладает большой вязкостью. Поэтому скорость движения масла в трубопроводах системы смазки обычно меньше, чем в трубопроводах других гидравлических систем, где рабочим телом является вода, керосин или бензин. При расчете этой системы, как и в предыдущем случае, давление в масляном баке можно принять равным атмосферному давлению рН на высоте полета H. Температура масла дана в задании. Давление среды, в которой работают подшипники, можно считать равным атмосферному давлению рН. 1. Основные понятия и расчётные формулы Весь поток жидкости можно разбить на множество элемен-тарных струек с бесконечно малыми поперечными сечениями, в которых из-за их малости параметры постоянны. Поэтому течение в элементарной струйке является одномерным: параметры зависят только от одной координаты, отсчитываемой вдоль оси струйки. В поперечных сечениях гидравлических элементов вычисляются средние параметры (скорость, давление), при использовании которых течение в гидравлическом элементе становится таким же, как в элементарной струйке. Таким образом, в гидравлике все гидравлические элементы заменяются элементарными струйками. Метод гидравлики – это метод элементарной струйки. Изменение параметров в поперечных сечениях гидравлических элементов учитывается в уравнении энергии коэффициентами осреднения (коэффициент Кориолиса). Закон сохранения массы в гидравлике записывается в виде уравнения неразрывности. Для установившегося режима на участке системы, ограниченном сечениями 1-1 и 2-2 (рис. 1, где 0-0 – плот- ность сравнения; z – высота сечения канала над плоскостью срав- нения), оно записывается в виде: 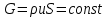 , (1) , (1)где G – массовый расход жидкости (масса жидкости, протекающая через поперечное сечение канала в единицу времени), кг/с; ρ – плотность жидкости, представляющая массу жидкости, заключенную в единице объема, кг/м3; u – среднерасходная скорость жидкости в сечении, м/с; S – площадь поперечного сечения канала, м2. Для несжимаемой жидкости плотность постоянна в любой точке потока, ввиду чего уравнение неразрывности может быть записано в виде: 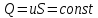 , ,где Q – объемный расход жидкости, м3/с. Уравнение энергии в гидравлике записывают в форме, которая называется уравнением Бернулли. Это уравнение записывается следующим образом: 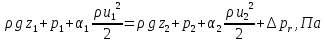 , ,где 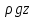 – энергия положения единицы объема жидкости в сечении, находящемся на высоте – энергия положения единицы объема жидкости в сечении, находящемся на высоте 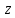 от плоскости сравнения 0-0, Па; от плоскости сравнения 0-0, Па; 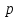 – энергия давления единицы объема жидкости в сечении, Па; – энергия давления единицы объема жидкости в сечении, Па;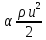 – кинетическая энергия единицы объема жидкости в сечении, Па; – кинетическая энергия единицы объема жидкости в сечении, Па; 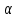 – коэффициент Кориолиса, учитывающий неравномерность распределения кинетической энергии по сечению; g – ускорение свободного падения (g = 9,81 м/с2); u – среднерасходная скорость потока в сечении, м/с; – коэффициент Кориолиса, учитывающий неравномерность распределения кинетической энергии по сечению; g – ускорение свободного падения (g = 9,81 м/с2); u – среднерасходная скорость потока в сечении, м/с;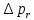 – потери механической энергии единицы объема жидкости в участке системы, между сечениями 1-1 и 2-2 за счет местных и (или) путевых сопротивлений, Па. – потери механической энергии единицы объема жидкости в участке системы, между сечениями 1-1 и 2-2 за счет местных и (или) путевых сопротивлений, Па.Различают два вида потерь полного давления на гидравлическом сопротивлении – местные и путевые, которые связаны формулой: 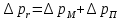 Местные потери проявляются в местах изменения формы, размеров канала или изменения направления движения потока, вычисляются по формуле Вейсбаха: 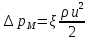 , (2) , (2)где 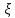 – коэффициент местного сопротивления, значение которого обычно определяется по справочным данным, в которых указывается сечение, определяющее потери; u – среднерасходная скорость в определяющем сечении. – коэффициент местного сопротивления, значение которого обычно определяется по справочным данным, в которых указывается сечение, определяющее потери; u – среднерасходная скорость в определяющем сечении.Путевые потери – это потери полного давления по длине трубы с прямой осью. Они вычисляются по формуле Дарси: 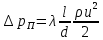 , (3) , (3)где 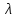 – коэффициент путевых потерь (коэффициент Дарси); l – длина трубы, м; d – диаметр трубы, м. – коэффициент путевых потерь (коэффициент Дарси); l – длина трубы, м; d – диаметр трубы, м.Значения коэффициента Кориолиса α и коэффициентов потерь ζ зависят от режима течения жидкости на рассматриваемом участке системы. Различают ламинарный и турбулентный режимы течения: при ламинарном режиме частицы жидкости движутся по почти параллельным траекториям со слабым перемешиванием слоев; в турбулентном течении наряду с главным направленным движением частицы жидкости совершают беспорядочные, хаотичные перемещения в продольном и поперечных направлениях. Поэтому турбулентное течение всегда сопровождается интенсивным перемешиванием жидкости и пульсациями скорости и давления. Режим течения жидкости в круглой трубе характеризуется числом Рейнольдса: 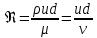 , (4) , (4)где ρ – плотность жидкости, кг/м3; u – среднерасходная скорость жидкости в трубе, м/с; d – диаметр трубы, м; μ – динамический коэффициент вязкости, Па·с; ν – кинематический коэффициент вязкости, м2/с. Ламинарный режим течения существует устойчиво при числах Рейнольдса Re ≤ 2300; при Re > 2300 ламинарное течение теряет устойчивость, при 2300 < Re < 4000 существует переходный режим течения, а при Re > 4000 течение становится турбулентным. При ламинарном течении коэффициент путевых потерь опре- деляют по формуле Пуазейля: 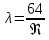 . (5) . (5)При турбулентном течении коэффициент путевых потерь вычисляется по формуле Блазиуса или Конакова: 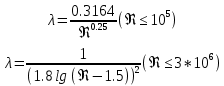 . (6) . (6)2. Расчёт гидравлической системы 2.1 Определение теплофизических характеристик рабочей жидкости Д 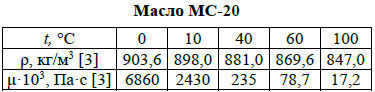 ля заданной температуры по справочным данным (работы [2, 3]): Рабочая температура масла 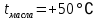 . Вычислим значения плотности и динамической вязкости для заданной температуры, применяя метод интерполяции. . Вычислим значения плотности и динамической вязкости для заданной температуры, применяя метод интерполяции.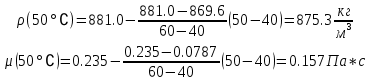 (7) (7)2.2 Определение атмосферного давления на высоте полёта Для заданной высоты расположения 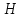 вычислим атмосферное давление вычислим атмосферное давление 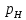 по формуле работы [4]: по формуле работы [4]: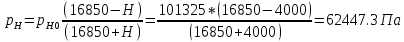 (8) (8)2.3 Расчёт скорости течения жидкости во всасывающей и напорной магистралях Выберем скорость течения жидкости в трубопроводах всасывающей 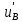 и напорной и напорной 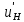 магистралей. Рекомендуются следующие значения для системы смазки ВРД: магистралей. Рекомендуются следующие значения для системы смазки ВРД: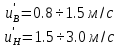 Выбранные значения скорости: 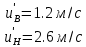 2.4 Расчёт внутреннего диаметра трубопроводов Используя уравнение расхода (1), рассчитаем внутренний диаметр трубопроводов всасывающей 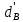 и напорной и напорной 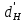 магистралей по формулам: магистралей по формулам: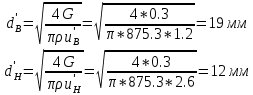 (9) (9)2.5 Уточнение внутреннего диаметра трубопроводов Определим ближайший внутренний диаметр трубопроводов всасывающей 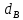 и напорной и напорной 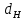 магистралей, выпускаемых промышленностью. Для системы смазки ВРД используются стальные или дюралюминиевые трубы. магистралей, выпускаемых промышленностью. Для системы смазки ВРД используются стальные или дюралюминиевые трубы. От масляного бака 1 до насоса 13 – всасывающая магистраль; от насоса 13 до форсунок – напорная. По ГОСТ 18475-82 для всасывающей магистрали возьмём трубу с внешним диаметром 20 мм с толщиной стенки 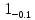 мм; для напорной – с внешним диаметром 13 мм с толщиной стенки мм; для напорной – с внешним диаметром 13 мм с толщиной стенки 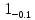 мм. мм.2.6 Уточнение скорости течения жидкости во всасывающей и напорной магистралях Для дальнейших расчётов возьмём самый неблагоприятный вариант, когда толщина стенок труб не совпадает с номинальной: меньше номинальной на 0.1 мм. 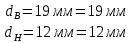 Тогда уточним значения скорости течения жидкости в соответствии с уточненными диаметрами трубопроводов по формулам: 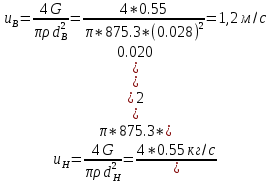 (10) (10)Уточненные значения скорости остались в пределах рекомендованных значений для системы смазки ВРД. 2.7 Определение расхода и скорости течения жидкости Определение осуществим после разветвления магистрали (после прохождения через тройники). В системе смазки ВРД после первого тройника 21 (рис.1) должен быть обеспечен расход масла к ближайшей форсунке 23, равный 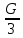 , и расход масла к двум другим форсункам, равный , и расход масла к двум другим форсункам, равный 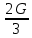 . После второго тройника 27 расход масла к каждой из двух оставшихся форсунок должен быть равен . После второго тройника 27 расход масла к каждой из двух оставшихся форсунок должен быть равен 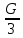 . .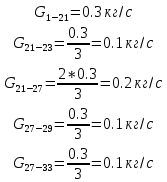 (11) (11)Рассчитаем скорости через расход: 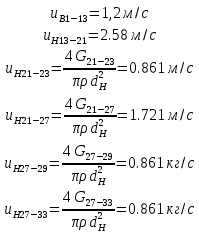 (12) (12)2.8 Определение режима течения жидкости Вычислим значение числа Рейнольдса для каждого участка по формуле(4): 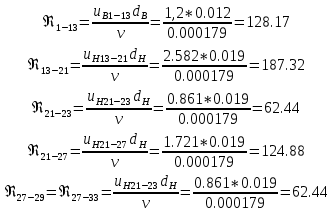 (13) (13)Все участки являются участками с ламинарным течением, так как все значения чисел Рейнольдса меньше 2300. Значит коэффициент Кориолиса для всех участков |

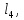
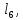 м
м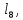
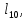 м
м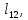 м
м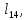 м
м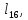
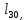 м
м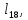
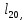 м
м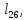 м
м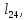 м
м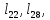
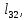 м
м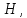 м
м