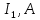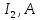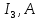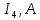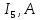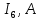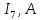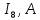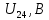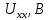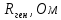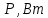Теория электрических цепей. ТР 1. Расчет сложной цепи постоянного тока
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
Учреждение образования Белорусский Государственный университет информатики и радиоэлектроники Кафедра теоретических основ электротехники Типовой расчет по курсу: «Теория электрических цепей» Тема: «Расчет сложной цепи постоянного тока» Проверил: Выполнил: Курулев А.П. Минск 2019 Исходные данные представлены в таблице:
Составить баланс мощностей. МЭГ напряжения найти ток в сопротивлении R5. Найти напряжение между узлами 2 и 4 (U24). Начертить схему согласно заданному варианту (источники тока включать параллельно заданной ветви). Изобразим граф схемы. При этом расположим узлы таким образом, чтобы ветви не пересекались (рис. 1). 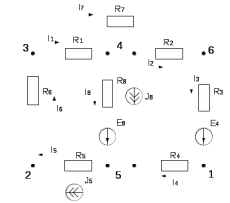 Рис. 1. Граф схемы Преобразовать схему к двухконтурной. На схеме (рис. 1) преобразуем источник тока J05 в источник напряжения E05: 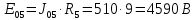 , , источник тока J08 – в источник напряжения E08: 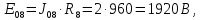 а также объединим последовательно включенные сопротивления R3 , R4 и R5, R6: 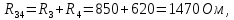 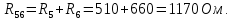 Полученная схема показана на рис.2. На этой схеме объединим источники напряжения E8 и E08: 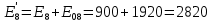 B. B.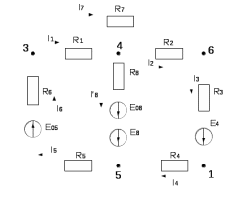 Рис. 2. Преобразованная схема цепи Пассивный треугольник 4-3-6 преобразуем в пассивную звезду (рис. 3), где 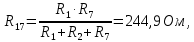 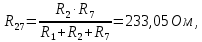 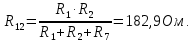  Рис. 3. Преобразование «треугольник-звезда» В результате этих преобразований схема будет иметь следующий вид (рис. 4): 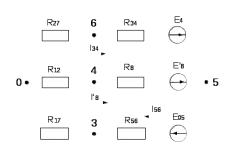 Рис. 4. Преобразованная схема цепи С целью дальнейшего упрощения схемы объединим последовательные сопротивления: 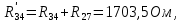 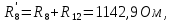 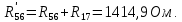 Схема примет следующий вид (рис. 5). 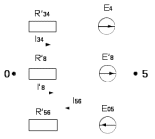 Рис. 5 Преобразованная схема Рассчитать двухконтурную схему, используя метод двух узлов. Для определения напряжения 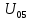 необходимо составить одно уравнение: необходимо составить одно уравнение: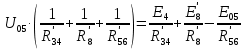 Отсюда 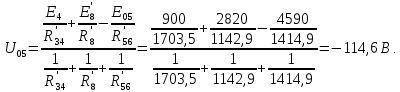 Определим токи в схеме рис. 5 на основании второго закона Кирхгофа: 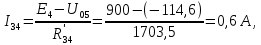 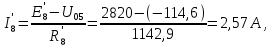 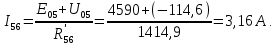 Разворачивая схему в обратном порядке найти токи в исходной схеме. По схеме рис. 4 определим напряжения между узлами 6, 4, 3: 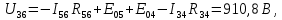 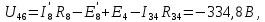 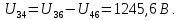 Определим токи I1, I2 и I7 (см. рис. 3): 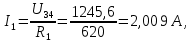 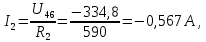 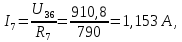 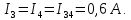 Для определения неизвестных токов I5, I6 и I8 составим уравнения по первому закону Кирхгофа (см. рис. 1) для узлов 4 и 5: для узла 4 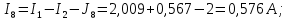 для узла 5 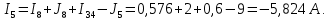 для узла 3 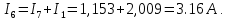 Найти напряжение между узлами 2 и 4 (U24). Для определения напряжения 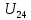 воспользуемся рис. 1. Тогда на основании второго закона Кирхгофа можно записать: воспользуемся рис. 1. Тогда на основании второго закона Кирхгофа можно записать: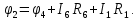 Отсюда 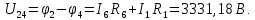 Определить суммарную мощность всех источников энергии 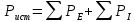 и суммарную мощность всех приемников энергии и суммарную мощность всех приемников энергии 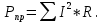 Проверить баланс мощностей Проверить баланс мощностей 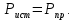 ЭДС положительна при совпадающих направлениях ЭДС и тока ветви и отрицательна при противоположном направлении ЭДС и тока ветви. Мощность источника тока определяется произведением тока данного источника и напряжения на его зажимах. Она положительна при противоположных направлениях на зажимах источника тока и тока источника. Мощность, выделяемая в активных сопротивлениях, всегда положительна и равна: 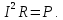 Баланс мощности записывается в виде 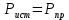 : :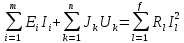 , ,где m - число источников ЭДС в схеме; n - число источников тока в схеме; f - число активных сопротивлений в схеме. Составим баланс мощностей для схемы рис. 1: 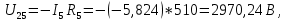 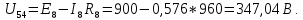 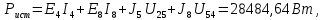 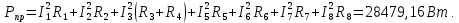 Определить токи в ветвях исходной схемы методом законов Кирхгофа. Составим систему уравнений, для узлов 1-4, 6 и контуров I, II, III (см. рис. 6): 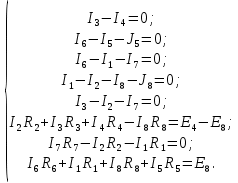 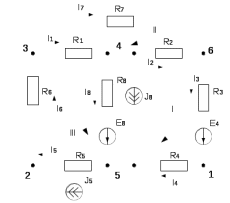 Рис. 6. Обозначение контуров и токов в ветвях Результаты работы в MathCAD:  Определить токи в ветвях исходной схемы методом контурных токов.  Определить токи в ветвях исходной схемы методом узловых напряжений. 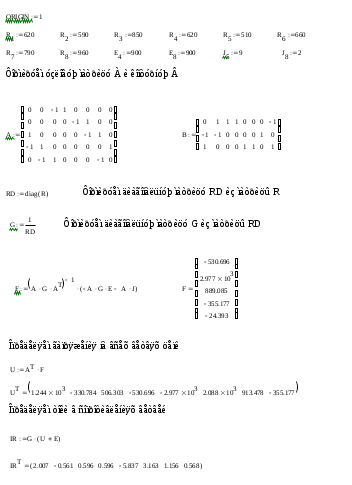 10. Определить ток в заданной ветви методом эквивалентного генератора напряжения в сопротивлении 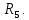 Определим напряжение эквивалентного генератора напряжения, для чего исключим сопротивление 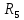 из исходной схемы (рис. 7). из исходной схемы (рис. 7).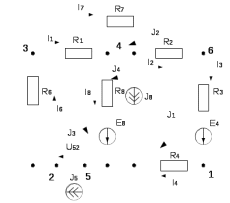 Рис. 7 Методом контурных токов определим токи в ветвях схемы. Уравнения имеют вид: 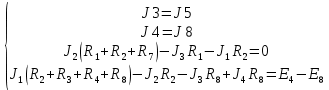 Подставляя числовые значения: 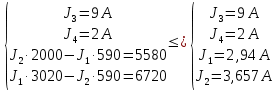 Отсюда выразим токи 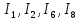 : :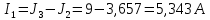 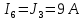 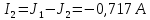 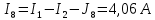 Находим 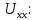 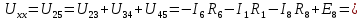 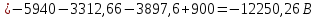 Далее, закоротив источники ЭДС и разомкнув ветви с источниками тока, находим эквивалентное сопротивление схемы относительно зажимов 2-5 ( 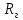 ) (рис. 8). ) (рис. 8). Рис. 8 Рис. 9 Эквивалентное сопротивление генератора 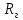 можно определить, преобразовав треугольник сопротивлений можно определить, преобразовав треугольник сопротивлений 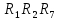 в эквивалентную звезду рис. 9: в эквивалентную звезду рис. 9: 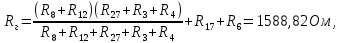 где 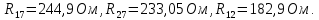 Ток в искомой цепи схемы (см. рис. 1) определяется по формуле: 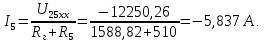 11. Для выбранного замкнутого контура схемы, включающего не менее 2-х источников ЭДС, построить в масштабе потенциальную диаграмму. Рассмотрим контур 5-5’-4-6-6’-1 (см. рис.10). Для удобства расчета потенциалов узлов выберем за базисную точку узел 5. Обход будем производить по часовой стрелке: 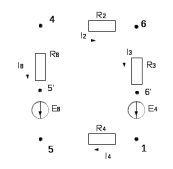 Рис. 10 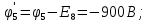 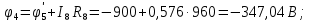 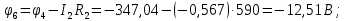 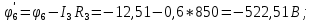 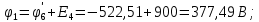 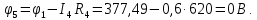 Для построения потенциальной диаграммы по оси абсцисс будем откладывать значения сопротивления элементов, а по оси ординат значения потенциалов точек. Базисную точку помещаем в начало координат (рис. 11). 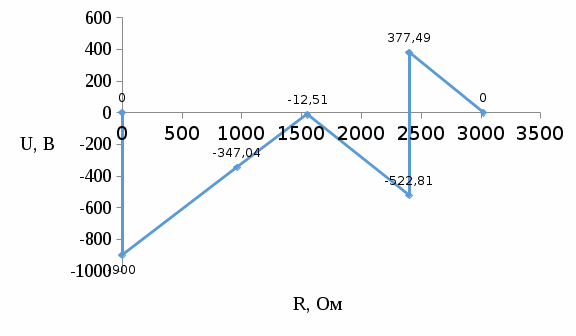 Рис. 11. Потенциальная диаграмма Таблица ответов:
Вывод В результате выполнения типового расчета различными методами расчета, были определены токи в электрической цепи. По полученным данным была построена потенциальная диаграмма. Если необходимо определить напряжения в узлах, а также рассчитать все токи цепи, то приемлемо использовать метод узловых напряжений. Он является несколько сложным для аналитических вычислений, однако легко считается на компьютерах. Если в цепи всего два узла, то можно применить, как частный случай данного метода, метод двух узлов. Если же интересует ток в какой-то определенной ветви, то целесообразно использовать метод эквивалентного генератора. ЛИТЕРАТУРА Беляцкий, А.Ф. Теория линейных электрических цепей / А.Ф. Беляцкий.– М. :Радиосвязь, 1986. Бессонов, Л.А. Теоретические основы электротехники: Электрические цепи / Л.А. Бессонов. – М., 2006. Новогородцев, А.Б. Теоретические основы электротехники / А.Б. Новогородцев. – СПБ.: 2006. Рекус, Г.Г. Основы электротехники и электроники в задачах и решениях / Г.Г. Рекус. – М., 2005. Теоретические основы электротехники : сборник задач / Н.В. Коровкин [и др.] – СПБ., 2006. |