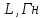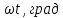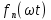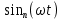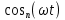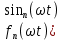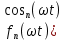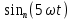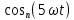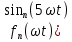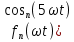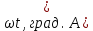РГР №3 Расчет сложной трехфазной цепи. РГР №4 Худяшов. Расчет сложной нелинейной цепи переменного тока
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Дальневосточный государственный университет путей сообщения» Кафедра "Электротехника, электроника и электромеханика" Расчетно-графическая работа По теме: «РАСЧЕТ СЛОЖНОЙ НЕЛИНЕЙНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА» Выполнил студент 2 курса, 622 группы: Худяшов Кирилл Алексеевич Вариант: 124 Проверил: Супрун Демьян Андреевич Хабаровск 2021 г. Задание на расчётно-графическую работу Для заданной электрической цепи необходимо: 1) Построить кривую тока в катушке и найти ее аналитическое выражение в виде ряда Фурье; 2) По полученному выражению построить на одном графике все гармонические составляющие и суммарную кривую; для сравнения на этом же графике привести кривую тока, найденную в п.1; 3) Рассчитать напряжение и ток на входе цепи; записать их выражения в виде рядов и найти действующие значения; 4) Рассчитать активную и полную мощности цепи; определить коэффициент мощности. Примечания: а) При расчете ограничиться первыми тремя гармониками; частоту основной гармоники принять равной 50 Гц; б) Потоком рассеяния и активными потерями катушки пренебречь. Построение кривой тока в катушке с ферромагнитным сердечником и анализ ее гармонического состава Основная кривая намагничивания
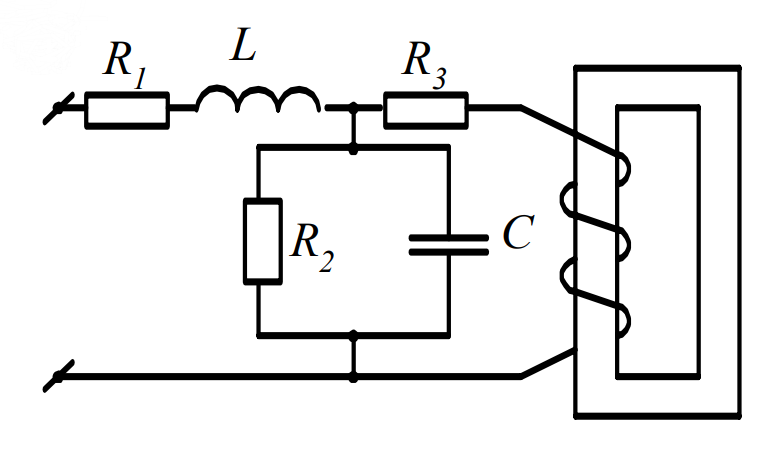 Рис 1. Расчетная схема Числовые значения параметров цепи
Кривая намагничивания 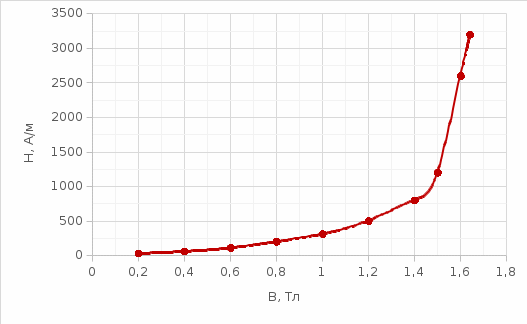 Кривую тока можно получить графически построением на основе вебер-амперной характеристики катушки и волновой диаграммы потокосцепления Прежде всего строим вебер-амперную характеристику катушки. Ее построение осуществляется путем пересчета координат основной кривой намагничивания. 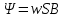 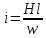 Точки вебер-амперной характеристики
Вебер амперная характеристика 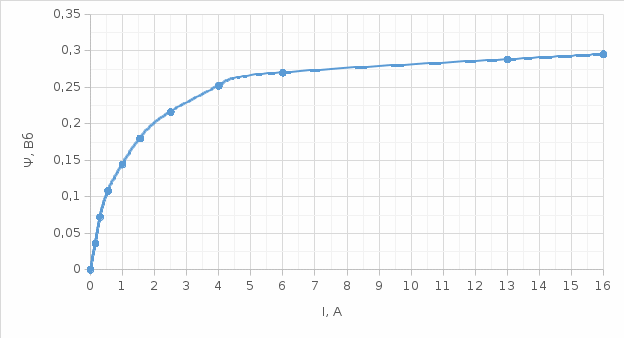 Далее строим кривую мгновенного значения потокосцепления. Согласно условиям, в катушке отсутствуют активные потери и поток рассеяния, поэтому при синусоидальном напряжении на ее зажимах потокосцепление отстает от напряжения на угол 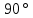 . .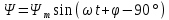 , ,Амплитуда потокосцепления: 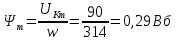 Начальная фаза: 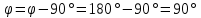 Мгновенное значение потокосцепления: 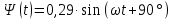 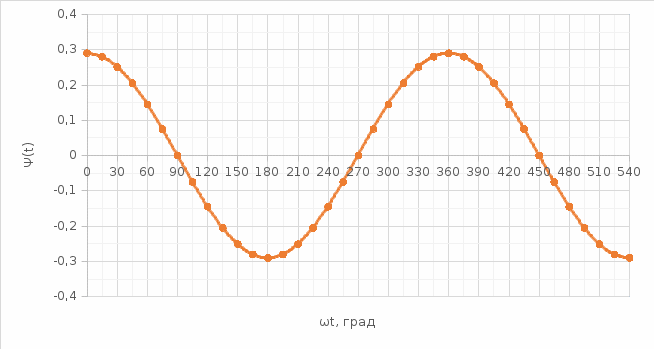 Теперь строим кривую тока в катушке. Задаемся произвольным значением угла 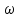 t. На кривой t. На кривой 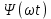 ему соответствует точка b, определяющая величину потокосцепления в данный момент . Проводя через нее горизонтальную прямую до пересечения с вебер-амперной характеристикой, получаем на ней точку с, абсцисса которой определяет величину тока. Откладывая этот ток при том же значении угла, получаем точку d , принадлежащую i( ему соответствует точка b, определяющая величину потокосцепления в данный момент . Проводя через нее горизонтальную прямую до пересечения с вебер-амперной характеристикой, получаем на ней точку с, абсцисса которой определяет величину тока. Откладывая этот ток при том же значении угла, получаем точку d , принадлежащую i(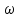 t) t) 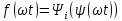 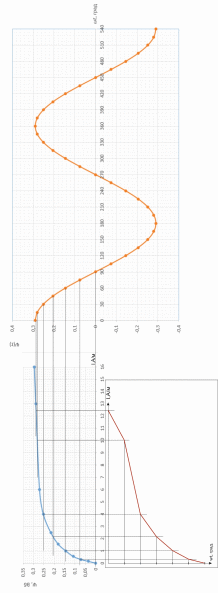 Кривая тока 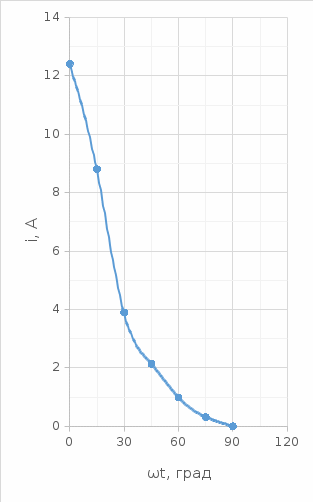 Анализ гармонического состава полученной кривой можно получить графоаналитическим методом Период функции f( 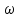 t) , равный 2 t) , равный 2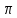 ,разбивается на x равных интервалов ,разбивается на x равных интерваловИзвестные формулы Эйлера-Фурье, определяющие коэффициенты тригонометрического ряда, заменяются следующими приближенными формулами: 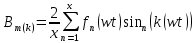 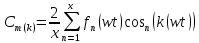 Амплитуды и начальные фазы гармоник определяются формулами: 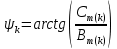 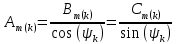 Расчет амплитудных значений гармонических составляющих
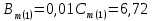
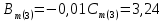
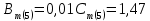 Теперь определяем амплитуды и начальные фазы гармоник 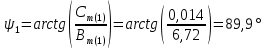 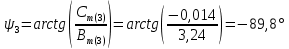 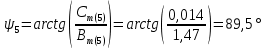 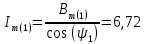 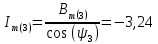 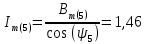 Следовательно, ряд тока, протекающего по катушке, имеет вид: 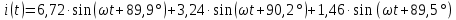 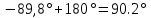 Построение гармонических составляющих и кривой несинусоидального тока
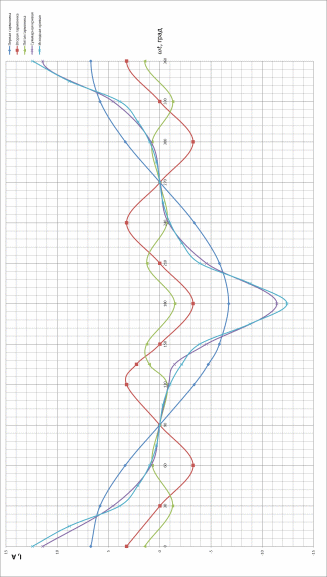 Расчет цепи несинусоидального тока  Рис 1. Расчетная схема Числовые значения параметров цепи
Расчет первой гармоники Комплексная амплитуда тока катушки: 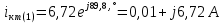 Здесь и далее применяем следующие обозначения: первые, один или два индекса, указывают участок схемы (например, K –- катушка), буква m – обозначение амплитудного значения, цифра в скобках – номер гармоники. Определяем реактивные и комплексные сопротивления участков цепи: 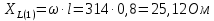 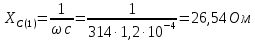 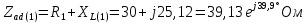 Амплитуды напряжений на зажимах катушки: 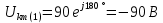 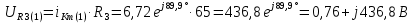 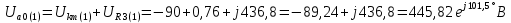 Применяя законы Ома и первый закон Кирхгофа для узла а, найдем токи во второй и третьей ветвях и на входе цепи: 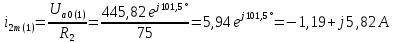 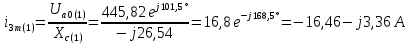 Ток на входе цепи: 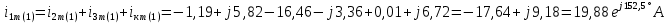 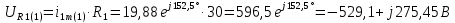 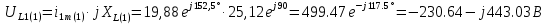 Напряжение на входе цепи: 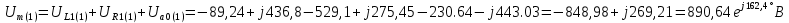 Мощности Комплексная мощность источника: 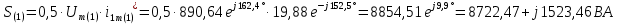 Мощность катушки: 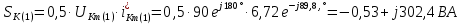 Мощности на участках цепи: 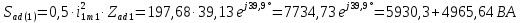 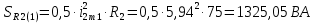 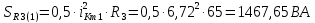 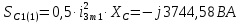 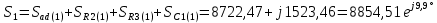 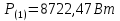 Расчет третьей и пятой гармоники Определяем реактивные и комплексные сопротивления: К=3 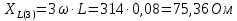 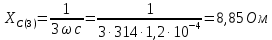 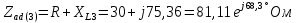 К=5 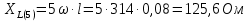 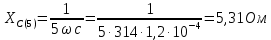 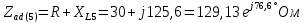 Кроме того, в кривой напряжения на катушке отсутствуют высшие гармоники, так как по заданию оно синусоидально с угловой частотой ω, поэтому принимаем: 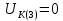 и и 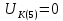 . .Расчет третьей гармоники: По мгновенному значению тока третьей гармоники, его комплексная амплитуда: 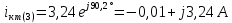 Напряжения: 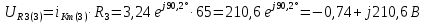 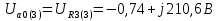 Применяя закона Ома и первый закон Кирхгофа для узла узла а, находим токи во второй и третьей ветвях и на входе цепи: 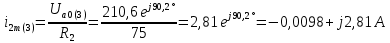 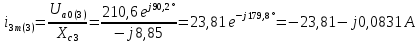 Ток на входе цепи: 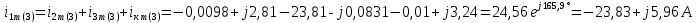 Напряжения: 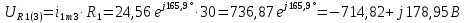 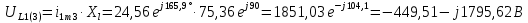 Напряжение на входе цепи: 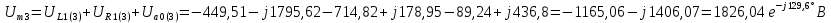 Далее рассчитываем мощности. Комплексная мощность источника: 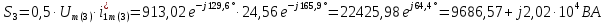 Мощности на отдельных участках цепи: 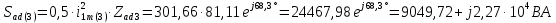 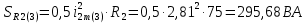 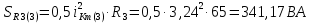 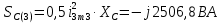 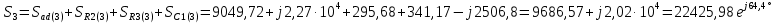 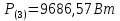 Ток 5-й гармоники: 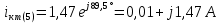 Напряжения: 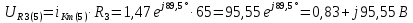 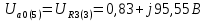 Применяя законы Ома и первый закон Кирхгофа для узла а, находим токи во второй и третей ветвях и на входе цепи: 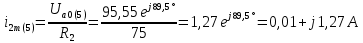 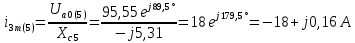 Ток на входе цепи: 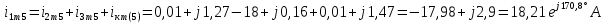 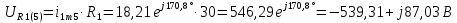 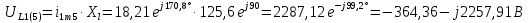 Напряжение на входе цепи: 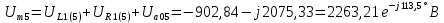 Далее рассчитываем мощности. Комплексная мощность источника: 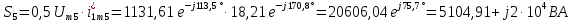 Мощности на отдельных участках цепи: 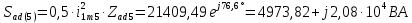 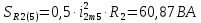 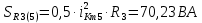 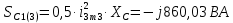 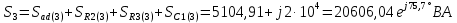 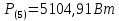 Суммарное действие гармоник Суммируя мгновенные значения отдельных гармоник, записываем в виде рядов ток и напряжение на входе цепи: 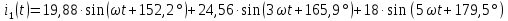 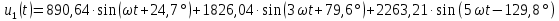 Действующие значения: 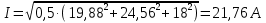 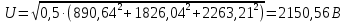 Полная мощность: 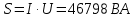 Активная мощность: 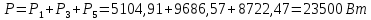 Коэффициент мощности: 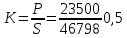 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

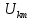 , В
, В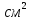
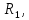 Ом
Ом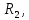 Ом
Ом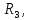 Ом
Ом