Сопр ответы. Расчёт статически неопределимых стержневых систем методом сил. Вывод канонических
 Скачать 463.15 Kb.
|
 1)Найти степень статической неопред. 2)После подсчета n необходимо выбрать ОС- статически определимую и кинематически неизменяемую( не механизм). Из заданной она получается путем снятия внешней нагрузки и отбрасыванием лишних связей.  3)Рисуем в соответствии с выбранной ОС эквивалентную систему,, равноценную заданной( деформируется также как и заданная, но статически определима). Получается нагружением ОС внешней нагрузкой и реакциями лишних связей. 4) Записать каноническое уравнение для ЭС: 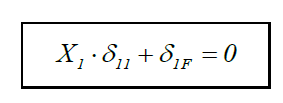 Найти Х1.  5) Рисуем ЭС. После раскрытия статической неопред. эпюра Мх обязательно должна быть знакопеременная, т.е иметь участки, где момент имеет сжатое волокно сверху и участки, где момент имеет сжатое волокно снизу. 6)Построить примерный вид изогнутой оси балки по эпюре Мх. Изогнутая ось обязательно должна проходить через точки закрепления.  В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения. Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:  где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е.  - это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи;  - перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.В методе сил реакцию k-ой связи принято обозначать через Xk. С учетом этого обозначения и в силу справедливости закона Гука перемещения можно представить в виде: где  - единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией  т.е. реакцией, совпадающей по направлению с Xk, но равной единице.Подставляя (2) в (1), получим:  Физический смысл уравнения (3): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю. Записывая выражения, аналогичные (3), для всей совокупности отброшенных связей, получим систему канонических уравнений метода сил:  Вид уравнения (4), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей. Коэффициенты системы канонических уравнений (4) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр. Все эти коэффициенты, как указывалось выше, представляют собой перемещения; коэффициенты, стоящие при неизвестных – единичные перемещения, а свободные члены – грузовые. Единичные перемещения делятся на главные, расположенные по главной диагонали и имеющие одинаковые индексы  и побочные ( ). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е.  .
Симметричными называют системы, образованные симметричными стержневыми конструкциями, к которым приложена симметричная нагрузка (рис.VII.11а.). Кососимметричными называют системы, образованные симметричными стержневыми конструкциями, к которым приложена обратносимметричная нагрузка (рис.VII.11б.), либо обратносимметричными конструкциями, к которым приложена симметричная (рис.VII.11в) либо кососимметричная (рис.VII.11г) нагрузка.   
|